গণিতের সূত্রাবলী (Math Formulas) ৫০০+ অতি প্রয়োজনীয় গণিতের সূত্র… টেবিল ও ক্যাটাগরি আকারে সাজানো (কম্পিউটার, ট্যাব ও স্মার্ট ফোন ভার্সন) (ষষ্ঠ থেকে একাদশ দ্বাদশ শ্রেণি পর্যন্ত সকল সূত্র ) এবং ইউনিভার্সিটি ভর্তি পরীক্ষার জন্য স্পেশাল সব সূত্র । এই বই দেখার পর আপনি "অসাধারন" কথাটা বলতে বাধ্য হবেন । কারন এই রকম সাজানো ভাবে বাজারের কোন বইয়ে বা গাইডে পাবেন না ।এখানে শুধু ইম্পরট্যান্ট সূত্র গুলো দেওয়া আছে। আপনি মনে মনে যেভাবে নোট করতে চেয়েছিলেন , বইটা ঠিক সেইভাবেই তৈরি করা হয়েছে। এই বইগুলোতে প্রশ্নের স্বাভাবিক নিয়মে সমাধান ও পাশাপাশি শর্ট কার্ট নিয়মও দেওয়া আছে।এবং সূত্র গুলোর মনে রাখার টেকনিক দেওয়া আছে। গনিত বিষয়টি কঠিন হলেও, সুত্র জানা থাকলে তা খুব সহজ হয়ে যায় । অধিকাংশ স্টুডেন্টদের অংক করার সময অনেক ঝামেলা পড়েতে হয় যেমন সূত্র মনে থাকেনা আবার কোন অংক দেখার সময় তা কোন সূত্র ব্যাবহার করা হয়েছে তা বুঝতে পারে না । তাছাড়া প্রয়োজনের সময় সূত্র মনেও আসে না আর বই তো সবসময় হাতে নিয়ে ঘুরা যায় না তাই সকল স্টুডেন্টদের জন্য আমার এই ই-বুক বা পিডিএফ বই । যা যে কোন স্থানে পড়তে পারবেন এবং যে কোন ডিভাইসে ওপেন করতে পারবেন … এখানে ৫০০+ অতি প্রয়োজনীয় গণিতের সূত্র একসাথে করে ক্যাটাগরি ও টেবিল আকারে সাজানো হয়েছে ,যাতে সহজে মনে থাকে …। প্রয়োজনীয় সূত্রগুলোর ব্যাখ্যা দেওয়া হয়েছে … এবং সূত্রের পাশাপাশি বিভিন্ন নিয়ম বা পদ্ধতি দেওয়া হয়েছে । সুতরাং যখনই দরকার হবে তখনই একবার করে চোখ বুলিয়ে নিতে পারবেন। আশা করি এভাবে একসময় সবগুলি সূত্রই মুখস্ত হয়ে যাবে।

1.  www.facebook.com/tanbir.ebooks
👦 www.facebook.com/tanbir.cox 👆 🎯www.tanbircox.blogspot.com
👆

2. 📚  www.facebook.com/tanbir.ebooks
👦 www.facebook.com/tanbir.cox 👆 🎯www.tanbircox.blogspot.com

3. 📚  www.facebook.com/tanbir.ebooks
👦 www.facebook.com/tanbir.cox 👆 🎯www.tanbircox.blogspot.com
ত্রিভু জক্ষেক্ষির দুই বাহু ও তাক্ষদর অন্তভু ুক্ত ক াণ কদওয়া থা ক্ষ েঃ
∆ কেি ABC এর কেিফ
=
1
2
ab sin 𝐶 =
1
2
𝑏𝑐 sin 𝐴 =
1
2
𝑐𝑎 sin 𝐵
ত্রিমত্রিবাহু ত্রিভু জ:
িমত্রিবাহু ∆ কেি ABC এর কেিফ
=
b
4
√4a2 − b2
বৃত্ত া কেিফ :
এ ত্রি চাপ ও চাক্ষপর প্রান্তত্রব্ু িংত্রিষ্ট বযািার্ু িারা কবত্রষ্টত কেিক্ষ বৃত্ত া ব া হয়।
বৃত্ত ার কেিফ =
𝜃
360 𝑜 ✕ 𝜋𝑟2

4. 📚  www.facebook.com/tanbir.ebooks
👦 www.facebook.com/tanbir.cox 👆 🎯www.tanbircox.blogspot.com
কব ন :
ক াক্ষনা আয়তক্ষেক্ষির কেক্ষ াক্ষনা বাহুক্ষ অে র্ক্ষর আয়তক্ষেিত্রিক্ষ ঐ বাহুর চতু ত্রদুক্ষ ক ারাক্ষ কে নবস্তুর
িৃত্রষ্ট হয়, তাক্ষ িমবৃত্তভূ ত্রম কব ন বা ত্রিত্র ণ্ডার ব া হয়। িমবৃত্তভূ ত্রম কব ক্ষনর দুই প্রান্তক্ষ বৃত্তা ার ত ,
বক্রত ক্ষ বক্রপৃষ্ঠ ব া হয় এবং িমগ্র ত ক্ষ পৃষ্ঠত ব া হয়।
এ ত্রি িমবৃৃ্ত্তভূ ত্রম কব ন োর ভূ ত্রমর বযািার্ু r এবং উচ্চতা h

5. 📚  www.facebook.com/tanbir.ebooks
👦 www.facebook.com/tanbir.cox 👆 🎯www.tanbircox.blogspot.com
(১) ভূ ত্রমর কেিফ = r2
(২) বক্রপৃক্ষষ্ঠর কেিফ = ভূ ত্রমর পত্ররত্রর্ ✕ উচ্চতা = 2rh
(৩) িম্পূণুতক্ষ র কেিফ বা িমগ্রতক্ষ র কেিফ
বা, পৃষ্ঠতক্ষ র কেিফ = (r2
✕ 2rh ✕ r2
) = 2r (r + h)
(৪) আয়তন = ভূ ত্রমর কেিফ ✕ উচ্চতা =πr2
h
িুষম বহুভু ক্ষজর কেিফ :
িুষম বহুভু ক্ষজর বাহুগুক্ষ ার দদ ুয িমান। আবার ক াণগুক্ষ া
িমান। n িংখ্য বাহুত্রবত্রিষ্ট িুষম বহুভু ক্ষজর ক ন্দ্র ও িীষু
ত্রব্ুগুক্ষ া কোগ রক্ষ n িংখ্য িমত্রিবাহু ত্রিভু জ উৎপন্ন ক্ষর।
িুতরাং বহুভু ক্ষজর কেিফ = n ✕ এ ত্রি ত্রিভু জ
কেক্ষিরক্ষেিফ ।
.⋅. n িংখ্য বাহুত্রবত্রিষ্ট িুষম বহুভু ক্ষজর কেিফ =
𝑛𝑎2
4
cot (
180 𝑜
𝑛
)

6. 📚  www.facebook.com/tanbir.ebooks
👦 www.facebook.com/tanbir.cox 👆 🎯www.tanbircox.blogspot.com

7. 📚  www.facebook.com/tanbir.ebooks
👦 www.facebook.com/tanbir.cox 👆 🎯www.tanbircox.blogspot.com
(a + b)2
এর জযাত্রমত্রত বযাখ্যা
বগুক্ষেিত্রির অংিগুক্ষ ার কেিফক্ষ র িমত্রষ্ট = (a + b) ✕ (a + b) = (a + b)
2
∴ (a + b)2
= a ✕ (a + b) + b ✕ (a + b)
= a2
+ ab + ab + b2
= a2
+ 2ab + b2
িম্পূণু বগুক্ষেিত্রির কেিফ = বগুক্ষেিত্রির অংিগুক্ষ ার কেিফক্ষ র িমত্রষ্ট
∴ (a + b)
2
= a2
+ 2ab + b2
িূি ১। (a + b)2
= a2
+ 2ab + b2
থায়, দুইত্রি রাত্রির কোগফক্ষ র বগু = ১ম রাত্রির বগু + ২ ✕ ১ম রাত্রি ✕ ২য় রাত্রি + ২য় রাত্রির বগু।
িূি ২। (a − b)2
= a2
− 2ab + b2
থায়, দুইত্রি রাত্রির ত্রবক্ষয়াগফক্ষ র বগু = ১ম রাত্রির বগু − ২ ✕ ১ম রাত্রি ✕ ২য় রাত্রি + ২য় রাত্রির বগু।
মন্তবয: িূি ১ ও িূি ২ হক্ষত কদখ্া োয় কে, a2
+ b2
এর িাক্ষথ 2ab অথবা −2ab কোগ রক্ষ এ ত্রি
পূণুবগু, অথুাৎ (a + b)2
অথবা (a − b)2
পাওয়া োয়। িূি ১ এ b এর স্থক্ষ −b বিাক্ষ িূি ২ পাওয়া
োয়: {a + (−b)}2
= a2
+ 2a(−b) + (−b)2
অথুাৎ, (a − b)2
= a2
− 2ab + b2
িূি ৩। a2
− b2
= (a + b)(a − b)
অথুাৎ দুইত্রি রাত্রির বক্ষগুর ত্রবক্ষয়াগফ = রাত্রি দুইত্রির কোগফ ✕ রাত্রি ত্রদুইত্রির ত্রবক্ষয়াগফ
িূি ৪। (x + a)(x + b) = x2
+ (a + b)x + ab
অথুাৎ, (x + a)(x + b) = x2
+ ( a ও b এর বীজগাত্রণত্রত কোগফ ) x + (a ও b এর গুণফ )
অনুত্রিদ্ধান্ত ১। a2
+ b2
= (a + b)2
− 2ab
অনুত্রিদ্ধান্ত ২। a2
+ b2
= (a − b)2
+ 2ab
অনুত্রিদ্ধান্ত ৩। (a + b)2
= (a − b)2
+ 4ab
🎯 (𝐚 + 𝐛) 𝟐
= a2
+ 2ab + b2
= a2
− 2ab + b2
+ 4ab = (𝐚 − 𝐛) 𝟐
+ 𝟒𝐚𝐛
অনুত্রিদ্ধান্ত ৪। (a − b)2
= (a + b)2
− 4ab
🎯 (a − b)2
= a2
− 2ab + b2
= a2
+ 2ab + b2
− 4ab = (𝐚 + 𝐛) 𝟐
− 𝟒𝐚𝐛
অনুত্রিদ্ধান্ত ৫। (a2
+ b2
) =
(a+b)2+(a−b)2
2
🎯 িূি ১ ও িূি ২ হক্ষত,
a2
+ 2ab + b2
= (a + b)2
a2
− 2ab + b2
= (a − b)2
কোগ ক্ষর, 2a2
+ 2b2
= (a + b)2
+ (a − b)2
বা, 2(a2
+ b2
) = (a + b)2
+ (a − b)2
a a+b b
a
a+b
b
a2 ab a
ab
b2 b
a b

8. 📚  www.facebook.com/tanbir.ebooks
👦 www.facebook.com/tanbir.cox 👆 🎯www.tanbircox.blogspot.com
িুতরাং (a2
+ b2
) =
(a+b)2+(a−b)2
2
অনুত্রিদ্ধান্ত ৬। 𝐚𝐛 = (
a+b
2
)2
− (
a−b
2
)2
🎯 িূি ১ ও িূত্র ২ হক্ষত,
a2
+ 2ab + b2
= (a + b)2
a2
− 2ab + b2
= (a − b)2
ত্রবক্ষয়াগ ক্ষর, 4ab = (a + b)2
− (a − b)2
বা, 𝐚𝐛 =
(a+b)2
4
−
(a−b)2
4
িুতরাং, 𝐚𝐛 = (
a+b
2
)2
− (
a−b
2
)2
🎯 অনুত্রিদ্ধান্ত ৬ প্রক্ষয়াগ ক্ষর কেক্ষ ান দুইত্রি রাত্রির গুণফ ক্ষ দুইত্রি রাত্রির বক্ষগুর ত্রবক্ষয়াগফ বা অন্তর
রূক্ষপ প্র াি রা োয়।
বগুিূক্ষির িম্প্রিারণ:
a + b+ c রাত্রিক্ষত ত্রতনত্রি পদ আক্ষে। এক্ষ (a+b) এবং c এ দুইত্রি পক্ষদর িমত্রষ্ট রূক্ষপ ত্রবক্ষবচনা রা োয়।
অতএব, িূি ১ প্রক্ষয়াগ ক্ষর a+b+c রাত্রিত্রির বগু ক্ষর পাই,
(a + b+c)2
= {(a + b)+c}2
= (a + b)2
+2(a + b)c + c2
= a2
+ b2
+ c2
+ 2ab + 2bc + 2ac.
িূি ৫। (a + b+c)2
= a2
+ b2
+ c2
+ 2ab + 2bc + 2ac.
অনুত্রিদ্ধান্ত ৭। a2
+ b2
+ c2
= (a + b+c)2
− 2(ab + bc + ac)
অনুত্রিদ্ধান্ত ৮। 2(ab + bc + ac) = (a + b+c)2
− (a2
+ b2
+ c2
)
(i) (a + b−c)2
= a2
+ b2
+ c2
+ 2ab − 2bc − 2ac
(ii) (a − b+c)2
= a2
+ b2
+ c2
− 2ab − 2bc + 2ac
(iii) (𝑎 − 𝑏 − 𝑐)2
= 𝑎2
+ 𝑏2
+ 𝑐2
− 2𝑎𝑏 + 2𝑏𝑐 − 2𝑎𝑐
ন িংবত্র ত িূিাবত্র
িূি ৬। (𝑎 + 𝑏)3
= 𝑎3
+ 3𝑎2
𝑏 + 3𝑎𝑏2
+ 𝑏3
= 𝑎3
+ 𝑏3
+ 3𝑎𝑏(𝑎 + 𝑏)
🎯 (𝑎 + 𝑏)3
= (𝑎 + 𝑏)(𝑎 + 𝑏)2
= (𝑎 + 𝑏)(𝑎2
+ 2𝑎𝑏 + 𝑏2
)
= 𝑎3
+ 3𝑎2
𝑏 + 3𝑎𝑏2
+ 𝑏3
= 𝑎3
+ 𝑏3
+ 3𝑎𝑏(𝑎 + 𝑏)
অনুত্রিদ্ধান্ত ৯। 𝑎3
+ b3
= (𝑎 + 𝑏)3
− 3ab(a + b)
িূি ৭। (𝑎 − 𝑏)3
= 𝑎3
− 3𝑎2
𝑏 + 3𝑎𝑏2
− 𝑏3
= 𝑎3
− 𝑏3
− 3𝑎𝑏(𝑎 − 𝑏)
🎯 (𝑎 − 𝑏)3
= (𝑎 − 𝑏)(𝑎 − 𝑏)2
= (𝑎 − 𝑏)(𝑎2
− 2𝑎𝑏 + 𝑏2
)
= 𝑎3
− 3𝑎2
𝑏 + 3𝑎𝑏2
− 𝑏3
= 𝑎3
− 𝑏3
− 3𝑎𝑏(𝑎 − 𝑏)
ে ত্রর: িূি ৬ এ 𝑏 এর স্থক্ষ −𝑏 বিাক্ষ িূি ৭ পাওয়া োয়:
{𝑎 + (−𝑏)}3
= (𝑎 − 𝑏)3
= 𝑎3
− 𝑏3
− 3𝑎𝑏(𝑎 − 𝑏)
অনুত্রিদ্ধান্ত ১০। 𝑎3
− 𝑏3
= (𝑎 − 𝑏)3
+ 3𝑎𝑏(𝑎 − 𝑏)
িূি ৮। 𝑎3
+ 𝑏3
= (𝑎 + 𝑏)(𝑎2
− 𝑎𝑏 + 𝑏2
)
িূি ৯। 𝑎3
− 𝑏3
= (𝑎 − 𝑏)(𝑎2
+ 𝑎𝑏 + 𝑏2
)
🎯 𝑎3
− 𝑏3
= (𝑎 − 𝑏)3
+ 3𝑎𝑏(𝑎 − 𝑏) = (𝑎 − 𝑏){(𝑎 − 𝑏)2
+ 3𝑎𝑏}

9. 📚  www.facebook.com/tanbir.ebooks
👦 www.facebook.com/tanbir.cox 👆 🎯www.tanbircox.blogspot.com
= (𝑎 − 𝑏)(𝑎2
+ 𝑎𝑏 + 𝑏2
)

10. 📚  www.facebook.com/tanbir.ebooks
👦 www.facebook.com/tanbir.cox 👆 🎯www.tanbircox.blogspot.com
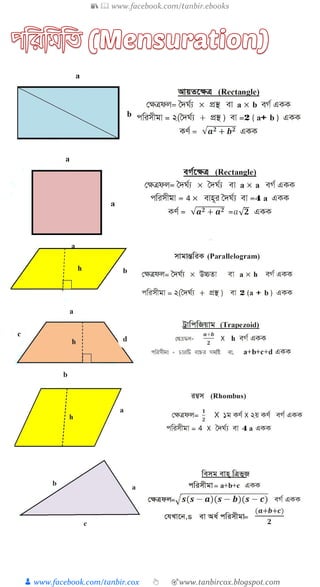
উৎপাদ : েত্রদ ক াক্ষনা বীজগত্রণতীয় রাত্রি দুই বা তক্ষতাত্রর্ রাত্রির গুণফ হয়, তাহক্ষ কিক্ষষাক্ত
রাত্রিগুক্ষ ার প্রক্ষতয ত্রিক্ষ প্রথম রাত্রির উৎপাদ বা গুণনীয় (Factor) ব া হয়। কেমন,
a
2
− b
2
= (a + b)(a - b), এখ্াক্ষন (a + b) ও (a - b) রাত্রি দুইত্রি (a
2
− b
2
) এর উৎপাদ ।
উৎপাদক্ষ ত্রবক্ষেষণ : েখ্ন ক াক্ষনা বীজগত্রণতীয় রাত্রিক্ষ িম্ভাবয দুই বা তক্ষতাত্রর্ ির রাত্রির
গুণফ রূক্ষপ প্র াি রা হয়, তখ্ন এ উৎপাদক্ষ ত্রবক্ষেষণ রা বক্ষ এবং ঐ রাত্রিগুক্ষ ার
প্রক্ষতয ত্রিক্ষ প্রথক্ষমাক্ত রাত্রির উৎপাদ ব া হয়। কেমন, x
2
+2x=x(x+2) [এখ্াক্ষন x ও (x+2)
উৎপাদ ]
উৎপাদ ত্রনণুক্ষয়র ত্রতপয় ক ৌি :
( ) ক াক্ষনা বহুপদীর প্রক্ষতয পক্ষদ িার্ারণ উৎপাদ থা ক্ষ তা প্রথক্ষম কবর ক্ষর ত্রনক্ষত হয়। কেমন :
(খ্) এ ত্রি রাত্রিক্ষ পূণু বগু আ াক্ষর প্র াি ক্ষর :
(গ) এ ত্রি রাত্রিক্ষ দুইত্রি বক্ষগুর অন্তররূক্ষপ প্র াি ক্ষর এবং 𝐚 𝟐
− 𝐛 𝟐
= (𝐚 + 𝐛)(𝐚 − 𝐛) িূি প্রক্ষয়াগ
ক্ষর :
( ) 𝒙 𝟐
+ (𝒂 + 𝒃)𝒙 + 𝒂𝒃 = (𝒙 + 𝒂)(𝒙 + 𝒃) িূিত্রি বযবহার ক্ষর:
(ঙ)𝒂𝒙 𝟐
+ 𝒃𝒙 + 𝒄 আ াক্ষরর বহুপদীর মর্যপদ ত্রবভত্রক্ত রণ পদ্ধত্রতক্ষত :
(চ) এ ত্রি রাত্রিক্ষ পূণু ন আ াক্ষর প্র াি ক্ষর:
(ে)𝒂 𝟑
+ 𝒃 𝟑
= (𝒂 + 𝒃)(𝒂 𝟐
‐ 𝒂𝒃 + 𝒃 𝟐
) এবং 𝒂 𝟑
− 𝒃 𝟑
= (𝒂 − 𝒃)(𝒂 𝟐
+ 𝒂𝒃 + 𝒃 𝟐
) িূি দুইত্রি
বযবহার ক্ষে্:
 a2
− 𝑏2
= (𝑎 + 𝑏)(𝑎 − 𝑏)
 𝑎3
+ 𝑏3
= (𝑎 + 𝑏)(𝑎2
− 𝑎𝑏 + 𝑏2
)
 𝑎3
− 𝑏3
= (𝑎 − 𝑏)(𝑎2
+ 𝑎𝑏 + 𝑏2
)
 𝑥2
+ 𝑞𝑥 + 𝑟 রাশিশিকে উৎপাদন শিকেষণ েরকে হকে , ধ্রি রাশি q সংখ্যাশিকে এমন
দুইশি উৎপাদকে (a ও b )প্রোি েরকে হকি যার সমশি িা যযাগফে x এর সহগ q (q= a+b)
এর সমান। এিং গুণফে ধ্রি রাশি r (r=a×b)এর সমান।
⇛ 𝑥2
+ 𝑞𝑥 + 𝑟 = 𝑥2
+ (𝑎 + 𝑏)𝑥 + 𝑎𝑏 = (𝑥 + 𝑎)(𝑥 + 𝑏)
1) q>0, r>0 হকে (𝑥 + 𝑎)(𝑥 + 𝑏)
2) q<0, r>0 হকে (𝑥 − 𝑎)(𝑥 − 𝑏)
3) q>0, r<0 হকে a ও b এর মকযয িড়শি + ও য ািশি – হকি।
 𝑝𝑥2
+ 𝑞𝑥 + 𝑟 = 𝑎𝑐𝑥2
+ (𝑏𝑐 + 𝑎𝑑)𝑥 + 𝑏𝑑 = (𝑎𝑥 + 𝑏)(𝑐𝑥 + 𝑑)
𝑥3
+ 𝑝𝑥2
+ 𝑞𝑥 + 𝑟 = 𝑥3
+ (𝑎 + 𝑏 + 𝑐)𝑥2
+ (𝑎𝑏 + 𝑏𝑐 + 𝑐𝑎)𝑥 + 𝑎𝑏𝑐
= (𝑥 + 𝑎)(𝑥 + 𝑏)(𝑥 + 𝑐)

11. 📚  www.facebook.com/tanbir.ebooks
👦 www.facebook.com/tanbir.cox 👆 🎯www.tanbircox.blogspot.com
 𝑥2
+ (𝑎 + 𝑏)𝑥 + 𝑎𝑏 = (𝑥 + 𝑎)(𝑥 + 𝑏) = 0 হকে এর মুেদ্বয় হকি x = -a , x = -b ।

 𝑎𝑥2
+ 𝑏𝑥 + 𝑐 = 0 এর মূেদ্বয় α ও β হকে,⇒ α + β = −
𝑏
𝑎
এিং α × β =
𝑐
𝑎
∴ সমীেরণ x2
− (α + β )𝑥 + αβ =0
 𝑎𝑥2
+ 𝑏𝑥 + 𝑐 = 0 সমীেরকণর এর মূেদ্বয় 𝑥 =
−𝑏 ± √𝑏2−4𝑎𝑐
2𝑎
( ) িুত্রবর্ামক্ষতা িাত্রজক্ষয় :
px-qy+qx-py ক িাজাক্ষনা হক্ষ া, px+qx-py-qy রূক্ষপ।
এখ্ন, px+qx-py-qy=x(p+q)-y(p+q)=(p+q)(x-y).
আবার, px-qy+qx-py ক িাজাক্ষনা হক্ষ া, px-py+qx-qy রূক্ষপ।
এখ্ন, px-py+qx-qy=p(x-y)+q(x-y)=(x-y)(p+q).
(খ্) এ ত্রি রাত্রিক্ষ পূণু বগু আ াক্ষর প্র াি ক্ষর :
x
2
+4xy+4y
2
=(x)
2
+2✕x✕2y+(2y)
2
=(x+2y)
2
=(x+2y)(x+2y)
(গ) এ ত্রি রাত্রিক্ষ দুইত্রি বক্ষগুর অন্তররূক্ষপ প্র াি ক্ষর এবং a
2
− b
2
িূি প্রক্ষয়াগ ক্ষর :
a
2
+2ab-2b-1
=a
2
+2ab+b
2
-b
2
-2b-1 [এখ্াক্ষন b
2
এ বার কোগ এবং এ বার ত্রবক্ষয়াগ রা হক্ষয়ক্ষে। এক্ষত রাত্রির
মাক্ষনর ক াক্ষনা পত্ররবতুন হয় না]
=(a
2
+2ab+b
2
)-(b
2
+2b+1)
=(a+b)
2
-(b+1)
2
=(a+b+b+1)(a+b-b-1)
=(a+2b+1)(a-1)
ত্রব ল্প ত্রনয়ম :
a
2
+2ab-2b-1 =(a
2
-1)+(2ab-2b)=(a+1)(a-1)+2b(a-1)
=(a-1)(a+1+2b) =(a-1)(a+2b+1)
( )x
2
+(a+b)x+ab=(x+a)(x+b) িূিত্রি বযবহার ক্ষর:
x
2
+7x+10=x
2
+(2+5)x+2✕5 =(x +2)(x+5)
(ঙ) এ ত্রি রাত্রিক্ষ ন আ াক্ষর প্র াি ক্ষর :
8x
3
+36x
2
+54x+27=(2x)
3
+3✕(2x)
2
✕3+3✕2x✕(3)
2
+(3)
3
=(2x+3)
3
=(2x+3)(2x+3)(2x+3)
(চ) a
3
+b
3
=(a+b)(a
2
-ab+b
2
) এবং a
3
-b
3
=(a-b)(a
2
+ab+b
2
)

12. 📚  www.facebook.com/tanbir.ebooks
👦 www.facebook.com/tanbir.cox 👆 🎯www.tanbircox.blogspot.com
৪.৫ x
2
+px+q আ াক্ষরর রাত্রির উৎপাদ
আমরা জাত্রন, x
2
+ (a + b) x + ab = (x + a)(x + b)| এই িূিত্রির বামপাক্ষির রাত্রির িাক্ষথ
x
2
+px+q এর তু না রক্ষ কদখ্া োয় কে, উভয় রাত্রিক্ষতই ত্রতনত্রি পদ আক্ষে, প্রথম পদত্রি x
2
ও
এর িহগ 1 (এ ), ত্রিতীয় বা মর্য পদত্রিক্ষত x আক্ষে োর িহগ েথাক্রক্ষম (a + b) ও p এবং
তৃতীয় পদত্রি x বত্রজুত, কেখ্াক্ষন েথাক্রক্ষম ab ও q আক্ষে।
x
2
+ (a + b) x + ab এর দুইত্রি উৎপাদ । অতএব, x
2
+px+q এরও দুইত্রি উৎপাদ হক্ষব।
মক্ষন ত্রর, x
2
+px+q এর উৎপাদ দুইত্রি (x + a) ও (x + b)
িুতরাং, x
2
+px+q=(x+a)(x+b)=x
2
+(a+b)x+ab
তাহক্ষ , p=a+b এবং q=ab
এখ্ন, x
2
+px+q এর উৎপাদ ত্রনণুয় রক্ষত হক্ষ , q ক এমন দুইত্রি উৎপাদক্ষ প্র াি রক্ষত
হক্ষব োর বীজগত্রণতীয় িমত্রষ্ট p হয়। এই প্রত্রক্রয়াক্ষ মর্যপদ ত্রবভাজন (Middle term breakup)
বক্ষ ।
x
2
+7x+12 রাত্রিত্রিক্ষ উৎপাদক্ষ ত্রবক্ষিস্নষণ রক্ষত হক্ষ 12 ক এমন দুইত্রি উৎপাদক্ষ প্র াি
রক্ষত হক্ষব োর িমত্রষ্ট 7 এবং গুণফ 12 হয়। 12 এর িম্ভাবয উৎপাদ কজাড়ািমূহ 1,12; 2,6,
ও (3,4)। এক্ষদর মক্ষর্য 3,4 কজাড়াত্রির িমত্রষ্ট (3 + 4) = 7 এবং গুণফ 3 ✕ 4 = 12
∴ x
2
+ 7x + 12 = (x + 3) (x + 4)
 ax3
+ 𝑏𝑥 + 𝑐 রাশিকে (x-m) রাশি দ্বারা ভাগ ের?
এখ্াকন (x-m) যে এমন এেশি রাশি দ্বারা গুন েরকে হকি যাকে গুণফকের প্রথম রাশি
এিং
ভাজ্য( ax3
+ 𝑏𝑥 + 𝑐 ) এর প্রথম রাশির(ax3
) সমান হয় । এখ্ন যয রাশি দ্বারা গুন
েরা হকয়ক যসশি ভাগফকে িসকি । এিং গুণফে ভাজ্য এর শনকে িশসকয় শিকয়াগ েরকে
হকি। এভাকি পযযায়ক্রকম ভাগ েকর যযকে হকি ।

13. 📚  www.facebook.com/tanbir.ebooks
👦 www.facebook.com/tanbir.cox 👆 🎯www.tanbircox.blogspot.com
অজ্ঞাে রাশি সমূকহর মান দ্বারা এোশযে যুগপৎ শসদ্ধ হকে ,সমীেরণ সমূহকে এেকে সহ
সমীেরণ িকে।
চ েঃ
আমরা জাত্রন, x+3=5 এ ত্রি িমী রণ । এত্রি িমার্ান রক্ষত হক্ষ আমরা অজ্ঞাত রাত্রি x এর
মান কবর ত্রর । এখ্াক্ষন অজ্ঞাত রাত্রি x এ ত্রি চ । আবার x+a=5 িমী রণত্রি িমার্ান
রক্ষত হক্ষ আমরা x এর মান ত্রনণুয় ত্রর a এর মান নয় । এখ্াক্ষন x ক চ ও a ক র্ুরব
ত্রহক্ষিক্ষব র্রা হয় । এক্ষেক্ষি x এর মান a এর মার্যক্ষম পাওয়া োক্ষব ।
এ চ ত্রবত্রিষ্ট িমী রণেঃ কে িত্রম রক্ষন এ ত্রি মাি অজ্ঞাত রাত্রি থাক্ষ তাাঁক্ষ এ চ
ত্রবত্রিষ্ট িমী রণ বা ির িমী রণ ব া হয় । কেমন x+3=5 িমী রক্ষণ x এ ত্রি মাি চ তা
এত্রি ির িমী রণ বা এ চ ত্রবত্রিষ্ট িমী রণ ।
িমী রণ ও অক্ষভদ
িমী রণ : িমী রক্ষণ িমান ত্রচক্ষের দুইপক্ষে দুইত্রি বহুপদী থাক্ষ , অথবা এ পক্ষে (প্রর্ানত
ডানপক্ষে) িূনয থা ক্ষত পাক্ষর। দুই পক্ষের বহুপদীর চ ক্ষ র িক্ষবুাচ্চ াত িমান নাও হক্ষত পাক্ষর।
িমী রণ িমার্ান ক্ষর চ ক্ষ র িক্ষবুাচ্চ াক্ষতর িমান িংখ্য মান পাওয়া োক্ষব। এই মান বা
মানগুক্ষ াক্ষ ব া হয় িমী রণত্রির মূ । এই মূ বা মূ গুক্ষ া িারা িমী রণত্রি ত্রিদ্ধ হক্ষব। এ াত্রর্
মূক্ষ র কেক্ষি এগুক্ষ া িমান বা অিমান হক্ষত পাক্ষর। কেমন, 𝑥2
− 5𝑥 + 6 = 0 িমী রণত্রির মূ
2,3। আবার (𝑥 − 3)2
= 0 িমী রক্ষণ x এর মান 3 হক্ষ ও এর মূ 3,3।
অক্ষভদ : িমান ত্রচক্ষের দুইপক্ষে িমান াতত্রবত্রিষ্ট দুইত্রি বহুপদী থাক্ষ । চ ক্ষ র িক্ষবুাচ্চ াক্ষতর
িংখ্যার কচক্ষয়ও অত্রর্ িংখ্য মাক্ষনর জনয অক্ষভদত্রি ত্রিদ্ধ হক্ষব। িমান ত্রচক্ষের উভয় পক্ষের মক্ষর্য
ক াক্ষনা কভদ কনই বক্ষ ই অক্ষভদ। কেমন, (𝑥 + 1)2
− (𝑥 − 1)2
= 4 এ ত্রি অক্ষভদ; এত্রি x এর
ি মাক্ষনর জনয ত্রিদ্ধ হক্ষব। তাই এই িমী রণত্রি এ ত্রি অক্ষভদ। প্রক্ষতয বীজগত্রণতীয় িূি এ ত্রি
অক্ষভদ। কেমন, (𝑎 + 𝑏)2
= 𝑎2
+ 2𝑎𝑏 + 𝑏2
, (𝑎 − 𝑏)2
= 𝑎2
− 2𝑎𝑏 + 𝑏2
, 𝑎2
− 𝑏2
=
(𝑎 + 𝑏)(𝑎 − 𝑏), (𝑎 + 𝑏)3
= 𝑎3
+ 3𝑎2
𝑏 + 3𝑎𝑏2
+ 𝑏3
ইতযাত্রদ অক্ষভদ।
ি িমী রণ অক্ষভদ নয়। অক্ষভক্ষদ িমান (=) ত্রচক্ষের পত্ররবক্ষতু '≡' ত্রচে বযবহৃত হয়। তক্ষব ি
অক্ষভদই িমী রণ বক্ষ অক্ষভক্ষদর কেক্ষিও িার্ারণত িমান ত্রচে বযবহার রা হয়।
িমী রণ ও অক্ষভক্ষদর পাথু য ত্রনক্ষচ কদওয়া হক্ষ া :
িমী রণ অক্ষভদ
১। িমান ত্রচক্ষের দুই পক্ষে দুইত্রি বহুপদী থা ক্ষত পাক্ষর
অথবা এ পক্ষে িূনয থা ক্ষত পাক্ষর।
২। উভয় পক্ষের বহুপদীর মািা অিমান হক্ষত পাক্ষর।
৩। চ ক্ষ র এ বা এ াত্রর্ মাক্ষনর জনয িমতাত্রি িতয
হয়।
৪। চ ক্ষ র মাক্ষনর িংখ্যা িবুাত্রর্ মািার িমান হক্ষত
পাক্ষর।
৫। ি িমী রণ অক্ষভদ নয়।
১। দুই পক্ষে দুইত্রি বহুপদী থাক্ষ ।
২। উভয় পক্ষে বহুপদীর মািা িমান থাক্ষ ।
৩। চ ক্ষ র মূ কিক্ষির ি মাক্ষনর জনয
িার্ারণত িমতাত্রি িতয হয়।
৪। চ ক্ষ র অিংখ্য মাক্ষনর জনয িমতাত্রি
িতয।
৫। ি বীজগত্রণতীয় িূিই অক্ষভদ।

14. 📚  www.facebook.com/tanbir.ebooks
👦 www.facebook.com/tanbir.cox 👆 🎯www.tanbircox.blogspot.com
এ াত িমী রক্ষণর িমার্ানেঃ
িমী রণ িমার্াক্ষনর কেক্ষি ক্ষয় ত্রি ত্রনয়ম প্রক্ষয়াগ রক্ষত হয় । এই ত্রনয়মগু জানা থা ক্ষ
িমী রক্ষণর িমার্ান ত্রনণুয় িহজতর হয় । ত্রনয়মগুক্ষ া হক্ষ ােঃ
১) িত্রম রক্ষনর উভয়পক্ষে এ ই িংখ্যা বা রাত্রি কোগ রক্ষ পেিয় িমান থাক্ষ ।
২) িমী রক্ষণর উভয়পে কথক্ষ এ ই িংখ্যা বা রাত্রি ত্রবক্ষয়াগ রক্ষ পেিয় িমান থাক্ষ ।
৩) িমী রক্ষণর উভয়পক্ষে এ ই িংখ্যা বা রাত্রি গুণ রক্ষ পেিয় িমান থাক্ষ ।
৪) িমী রক্ষণর উভয়পেক্ষ অিূনয এ ই িংখ্যা বা রাত্রি িারা ভাগ রক্ষ পেিয় িমান থাক্ষ ।
এ াত িমী রক্ষণর বযবহারেঃ
বাস্তবত্রভত্রত্ত িমিযা িমার্াক্ষন অজ্ঞাত িংখ্যা ত্রনণুক্ষয়র জনয এর পত্ররবক্ষতু চ র্ক্ষর ত্রনক্ষয় িমিযায়
প্রদত্ত িতুানুিাক্ষর িমী রণ গঠন রা হয় । তারপর িমী রণত্রি িমার্ান রক্ষ ই চ ত্রির মান
অথুাৎ অজ্ঞাত িংখ্যাত্রি পাওয়া োয় ।
এ চ ত্রবত্রিষ্ট ত্রি াত িমী রণেঃ
আ াক্ষরর িমী রণক্ষ এ চ ত্রবত্রিষ্ট ত্রি াত িমী রণ ব া হয় ।
ত্রি াত িমী রক্ষণর বামপে এ ত্রি ত্রিমাত্রি বহুপদী ।
(১) প্রত্রতস্থাপন পদ্ধত্রত
( ) কেক্ষ াক্ষনা িমী রণ কথক্ষ চ দুইত্রির এ ত্রির মান অপরত্রির মার্যক্ষম প্র াি রা।
(খ্) অপর িমী রক্ষণ প্রাপ্ত চ ক্ষ র মানত্রি স্থাপন ক্ষর এ চ ত্রবত্রিষ্ট িমী রণ িমার্ান রা।
(গ) ত্রনণুীত িমার্ান প্রদত্ত িমী রণ দুইত্রির কেক্ষ াক্ষনা এ ত্রিক্ষত বত্রিক্ষয় অপর চ ক্ষ র মান ত্রনণুয়
রা।
(২) অপনয়ন পদ্ধত্রত
এই পদ্ধত্রতক্ষত ত্রনক্ষচর র্াপগুক্ষ া অনুিরণ ক্ষর িমার্ান রা োয় :
( ) প্রদত্ত উভয় িমী রণক্ষ এমন দুইত্রি িংখ্যা বা রাত্রি িারা পৃথ ভাক্ষব গুণ রক্ষত হক্ষব কেন
কেক্ষ াক্ষনা এ ত্রি চ ক্ষ র িহক্ষগর িাংত্রখ্য মান িমান নয়।
(খ্) এ ত্রি চ ক্ষ র িহগ এ ই ত্রচেত্রবত্রিষ্ট হক্ষ িমী রণ পরস্পর ত্রবক্ষয়াগ, অনযথায় কোগ রক্ষত
হক্ষব। ত্রবক্ষয়াগফ ৃ ত (বা কোগফ ৃ ত) িমী রণত্রি এ ত্রি এ চ ত্রবত্রিষ্ট ির িমী রণ হক্ষব।
( ) ির িমী রণ িমার্াক্ষনর ত্রনয়ক্ষম চ ত্রির মান ত্রনণুয় রা।
(ঙ) প্রাপ্ত চ ক্ষ র মান প্রদত্ত কেক্ষ াক্ষনা এ ত্রি িমী রক্ষণ বত্রিক্ষয় অপর চ ক্ষ র মান ত্রনণুয় রা।

15. 📚  www.facebook.com/tanbir.ebooks
👦 www.facebook.com/tanbir.cox 👆 🎯www.tanbircox.blogspot.com
এই যরকণর অংে পরীক্ষায় MCQ শহসাকি আসকে , সামাযাকনর যক্ষকে MCQ এর োরশি
Answer Choice এ x ও y এর োরকজ্াড়া মান যদওয়া থােকি। এখ্ন প্রকেযে যজ্াড়া
মান অথযাৎ x ও y এর মান প্রকে যদওয়া দুশি সমীেরকণর যয যোন এেশিকে(কয
সমীেরণশি অকপক্ষােৃ ে সহজ্) িসান। এিং যদখ্ুন যোন মাকনর জ্নয সমীেরণশি িূনয
হয়। যয মাকনর জ্নয সমীেরণশি িূনয হকি যসই মানশি অপর সমীেরকণও িশসকয় যদখ্ুন
িূনয হয় শেনা , যশদ যোণ মাকনর জ্নয উভয় সমীেরণ িূনয হয় োহকে সশিে উত্তর হকি
যসশি।
বাস্তব িমিযা িমার্াক্ষন বীজগাত্রণত্রত িূি গঠন ও প্রক্ষয়াগ
( ) প্রথক্ষমই িত ুতার িাক্ষথ িমিযাত্রি পেুক্ষবেণ ক্ষর এবং মক্ষনাক্ষোগ িহ াক্ষর পক্ষড় ক ানগুক্ষ া
অজ্ঞাত এবং ী ত্রনণুয় রক্ষত হক্ষব তা ত্রচত্রেত রক্ষত হক্ষব।
(খ্) অজ্ঞাত রাত্রিগুক্ষ ার এ ত্রিক্ষ কেক্ষ াক্ষনা চ (র্ত্রর 𝑥) িারা িূত্রচত রক্ষত হক্ষব। অতেঃপর
িমিযাত্রি ভাক্ষ াভাক্ষব অনুর্াবন ক্ষর অনযানয অজ্ঞাত রাত্রিগুক্ষ াক্ষ ও এ ই চ 𝑥 এর মার্যক্ষম
প্র াি রক্ষত হক্ষব।
(গ) িমিযাক্ষ েু দ্র েু দ্র অংক্ষি ত্রবভক্ত ক্ষর বীজগাত্রণত্রত রাত্রি িারা প্র াি রক্ষত হক্ষব।
( ) প্রদত্ত িতু বযবহার ক্ষর েু দ্র েু দ্র অংিগুক্ষ াক্ষ এ ক্ষি এ ত্রি িমী রক্ষণ প্র াি রক্ষত হক্ষব।
(ঙ) িমী রণত্রি িমার্ান ক্ষর অজ্ঞাত রাত্রি 𝑥 এর মান ত্রনণুয় রক্ষত হক্ষব।
বাস্তব িমিযা িমার্াক্ষন ত্রবত্রভন্ন িূি বযবহার রা হয়। িূিগুক্ষ া ত্রনক্ষচ উক্ষ খ্ রা হক্ষ া :
(১) কদয় বা প্রাপয ত্রবষয় :
কদয় বা প্রাপয, A = qn িা া
কেখ্াক্ষন, q = জনপ্রতি দেয় বা প্রাপ্য টাকার পতরমাণ n = দ াককর সংখ্যা
(২) িময় ও াজ ত্রবষয় :
ক্ষয় জন ক া এ ত্রি াজ িম্পন্ন রক্ষ , াক্ষজর পত্ররমাণ, W = qnx
কেখ্াক্ষন, q=প্রক্ষতযক্ষ এ িমক্ষয় াক্ষজর কে অংি িম্পন্ন ক্ষর,
n= াজ িম্পাদন ারীর িংখ্যা
x= াক্ষজর কমাি িময়
W=n জক্ষন x িমক্ষয় াক্ষজর কে অংি িম্পন্ন ক্ষর

16. 📚  www.facebook.com/tanbir.ebooks
👦 www.facebook.com/tanbir.cox 👆 🎯www.tanbircox.blogspot.com
(৩) িময় ও দূরত্ব ত্রবষয় :
ত্রনত্রদুষ্ট িমক্ষয় দূরত্ব, 𝑑 = 𝑣𝑡.
কেখ্াক্ষন, v = প্রত্রত ন্টায় গত্রতক্ষবগ , t = কমাি িময়
(৪) ন ও কচৌবাচ্চা ত্রবষয় :
ত্রনত্রদুষ্ট িমক্ষয় কচৌবাচ্চায় পাত্রনর পত্ররমাণ, Q(t)= Q_0±qt
কেখ্াক্ষন,, Q_0=নক্ষ র মুখ্ খ্ুক্ষ কদওয়ার িময় কচৌবাচ্চায় জমা পাত্রনর পত্ররমাণ।
q=প্রত্রত এ িমক্ষয় ন ত্রদক্ষয় কে পাত্রন প্রক্ষবি ক্ষর অথবা কবর হয়।
t=অত্রতক্রান্ত িময়।
Q(t)= t িমক্ষয় কচৌবাচ্চায় পাত্রনর পত্ররমাণ (পাত্রন প্রক্ষবি হওয়ার িক্ষতু ’+’ ত্রচে এবং পাত্রন কবর
হওয়ার িক্ষতু ‘-’ ত্রচে বযবহার রক্ষত হক্ষব)।
৫। িত রা অংি ত্রবষয় :
p=br.
কেখ্াক্ষন, b=কমাি রাত্রি
r=িত রা ভগ্াংি=s/100=s%
p=িত রা অংি=b এর s%
৬। াভ-েত্রত ত্রবষয় :
𝑆 = 𝐶(𝐼 ± 𝑟)
াক্ষভর কেক্ষি, 𝑆 = 𝐶(𝐼 + 𝑟)
েত্রতর কেক্ষি, 𝑆 = 𝐶(𝐼 − 𝑟)
কেখ্াক্ষন, S = ত্রবক্রয়মূ য
C = ক্রয়মূ য
I= াভ বা মুনাফা
r= াভ বা েত্রতর হার
(৭) ত্রবত্রনক্ষয়াগ-মুনাফা ত্রবষয় :
ির মুনাফার কেক্ষি,
𝐼 = 𝑃𝑛𝑟
𝐴 = 𝑃 + 𝐼 = 𝑃 + 𝑃𝑛𝑟 = 𝑃(1 + 𝑛𝑟),
চক্রবৃত্রদ্ধ মুনাফার কেক্ষি,
𝐴 = 𝑃(1 + 𝑟) 𝑛
কেখ্াক্ষন, I=n িময় পক্ষর মুনাফা
n=ত্রনত্রদুষ্ট িময়
P=মূ র্ন
r=এ িমক্ষয় এ মূ র্ক্ষনর মুনাফা
A=n িময় পক্ষর মুনাফািহ মূ র্ন

17. 📚  www.facebook.com/tanbir.ebooks
👦 www.facebook.com/tanbir.cox 👆 🎯www.tanbircox.blogspot.com
িহুপদী ও োর ঘাে (Polynomial and its degree) : িহুপদী এে যরকনর
িীজ্গাশণশেে রাশি (Expression) । একে এে িা এোশযে পদ (element) থােকে পাকর ।
এে িা এোশযে েেকের (variable) যেিেমাে যনাত্মে পূণযসাংশখ্যে ঘাে ও যোন ধ্রুিকের
(constant) গুণফে হে িহুপদীর শিশভন্ন পদ । িহুপদীর পদগুকোর সকিযাচ্চ ঘােকে িহুপদীয়
ঘাে (Degree) িকে ।
এে েেকের িহুপদী : এর প্রশে পকদ শুযুমাে এেশি েেকের শিশভন্ন পূণয সাংশখ্যে ঘাে ও
ধ্রুিে থাকে । যযমন :
a0x
n
+a1x
n-1
+a2x
n-2
+ ......+anএেশি এে েেকের িহুপদী যযখ্াকন x েেে ।
a0, a1, a2, ...... an ∈ R হে ধ্রুিে যযখ্াকন a0 ≠ 0 । n হে x এর সিযাশযে ঘাে । েক্ষণীয়, x
এর ঘাে েখ্নও ঋণাত্মে হকে পারকি না । a0যে মুখ্য সহগ িো হয় । এে েেে x-শিশিি
এরূপ িহুপদী রাশিকে f(x) দ্বারাও প্রোি েরা হয় ।
িহুপদী সমীেরণ (Polynomial Equation) :
a0x
n
+a1x
n-1
+a2x
n-2
+ ......+an = 0 আোকরর সমীেরণকে িহুপদী সমীেরণ িকে ।
x এর যয মানগুকোর জ্নয িহুপদী সমীেরণশি শসদ্ধ হয়, অথযাৎ িহুপদী রাশিশির মান িূনয হয়, ঐ
মানগুকোকে িহুপদী সমীেরকণর মূে (Roots) িো হয় ।
n = 1,2,3 এর জ্নয িহুপদী সমীেরণশিকে যথাক্রকম সরে সমীেরণ (Linear equation),
শদ্বঘাে সমীেরণ (quadratic equation), শেঘাে সমীেরণ (cubic equation) িো হয় ।
িহুপদী সমীেরকণর উপপাদয (Theorems of polynomial equations) :
িীজ্গশণকের যমৌশেে উপপাদয (Fundamental theorem of algebra) :
প্রশেশি িহুপদী সমীেরকণর অন্তে এেশি মূে (িাস্তি শেংিা জ্শিে) থাকে ।
n ঘাে শিশিি িহুপদী সমীেরকণ n সংখ্যে মূে আক (িাস্তি শেংিা জ্শিে) । েকি সি মূেগুকো
শভন্ন নাও হকে পাকর ।
ভাগকিষ উপপাদয (Remainder theorem) : যশদ যোন িহুপদী f(x) যে x-a দ্বারা ভাগ েরা
হয়, েকি ভাগকিষ হকি f(a) ।
উৎপাদে উপপাদয (Factor theorem) : যশদ a, িহুপদী সমীেরণ f(x) এর এেশি মূে হয়
েকি (x-a) িহুপদী f(x) এর এেশি উৎপাদে হকি ।
অনুিন্ধী মূে উপপাদয (Conjugate pairs theorem) : a+ib যোন িহুপদী সমীেরকণর জ্শিে
মূে হকে এর অনুিন্ধী a-ib ও সমীেরকণর মূে হকি । এিং a+√b এেশি মূে হকে (যযখ্াকন √b
অমূেদ), এর অনুিন্ধী a-√b ও সমীেরকণর এেশি মূে হকি ।
িহুপদীর মূে সহগ সম্পেয : যশদ a,b,c,d, ...... k যোন িহুপদী সমীেরণ p0x
n
+p1x
n-
1
+p2x
n-2
+ ...... +pnএর মূে হয় েকি,
= a+b+c+ ...... + k = - p1/p0
= ab+bc+cd+ ...... = P2/P0
a×b×c×d×......×k = (-1)
n
(pn/p0)

18. 📚  www.facebook.com/tanbir.ebooks
👦 www.facebook.com/tanbir.cox 👆 🎯www.tanbircox.blogspot.com
শদ্বঘাে সমীেরণ (Quadratic equation) : িহুপদী সমীেরকণর ঘাে 2 হকে োকে শদ্বঘাে
সমীেরণ িকে । এে েেেশিশিি শদ্বঘাে সমীেরকণর আদিয রূপ-
ax
2
+bx+c = 0; যযখ্াকন a≠0; a,b,c মূেদ সংখ্যা
উক্ত সমীেরণ সমাযান েরকে x এর দুইশি মান পাওয়া যাকি অথযাৎ শদ্বঘাে সমীেরকণর দুইশি মূে
হকি- এিং
শদ্বঘাে সমীেরকণর মূে-সহগ সম্পেয :
ax
2
+bx+c = 0 সমীেরকণর মূে দুইশি α এিং β (α>β) হকে,
= α+β = -b/a = -
αβ = c/a =
শদ্বঘাে সমীেরকণর মূকের প্রেৃ শে (Nature of the roots) : আমরা জ্াশন, ax
2
+bx+c =
0 শদ্বঘাে সমীেরকণর মূে, x = । এখ্াকন, (b
2
-4ac) এর মান পযযাকোেনা েরকেই
শদ্বঘাে সমীেরকণর মূেদ্বকয়র প্রেৃ শে জ্ানা যায় । এজ্নয (b
2
-4ac) যে শদ্বঘাে সমীেরকণর
শনশ্চায়ে িা শনরূপে (Discriminant) িো হয় ।
যশদ b
2
-4ac=0 ⇒ b
2
=4ac হয় েকি মূে দুইশি হকি –b/2a এিং –b/2a । অথযাৎ মূে দুইশি
িাস্তি, মূেদ ও সমান হকি ।
b
2
-4ac>0 ⇒ b
2
>4ac হকে মূেদ্বয় িাস্তি ও অসমান হকি ।
b
2
-4ac<0 ⇒ b
2
<4ac হকে মূেদ্বয় অনুিন্ধী জ্শিে সংখ্যা হকি ।
(b
2
-4ac) পূণযিগয হকে মূেদ্বয় িাস্তি, মূেদ ও অসমান হকি ।
c = 0 হকে এেশি মূে 0 হকি ।
b = 0 হকে মূে দুইশি হকি √(-c/a) এিং -√(-c/a) অথযাৎ মূে দুইশির মান সমান শেন্তু শিপরীে
শেহ্নশিশিি হকি । েক্ষণীয়, একক্ষকে a ও c এেই শেহ্নযুক্ত হকে মূেদ্বয় জ্শিে এিং শিপরীে
শেহ্নযুক্ত হকে মূেদ্বয় িাস্তি হকি ।
শদ্বঘাে সমীেরকণর সাযারণ মূে থাোর িেয :
a1x
2
+b1x+c1=0 ও a2x
2
+b2x+c2=0 সমীেরণদ্বকয়র-
এেশি মূে সাযারণ হকি যশদ (a1b2-a2b1)(b1c2-b2c1) = (c1a2-c2a1)
2
হয় ।
উভয় মূেই সাযারণ হকি যশদ a1/a2 = b1/b2 = c1/c2হয় ।
শদ্বঘাে সমীেরণ গিন : শদ্বঘাে সমীেরকণর দুইশি মূে যদয়া থােকে ো যথকে শদ্বঘাে
সমীেরণশি গিন েরা যায় । সমীেরণশি হকি-
x
2
- (মূেদ্বকয়র যযাগফে)x + (মূেদ্বকয়র গুণফে) = 0
অথযাৎ শদ্বঘাে সমীেরকণর দুইশি মূে α ও β হকে সমীেরণশি হকি-
x
2
- (α+β)x + αβ = 0
শেঘাে সমীেরণ Cubic equation) : িহুপদী সমীেরকণর ঘাে 3 হকে োকে শেঘাে
সমীেরণ িকে । এে েেেশিশিি শেঘাে সমীেরকণর আদিয রূপ-
ax
3
+bx
2
+cx+d = 0; যযখ্াকন a≠0; a,b,c,d মূেদ সংখ্যা
শেঘাে সমীেরকণর মূে-সহগ সম্পেয : ax
3
+bx
2
+cx+d = 0 সমীেরকণর মূেেয় α,β,γ
হকে-

19. 📚  www.facebook.com/tanbir.ebooks
👦 www.facebook.com/tanbir.cox 👆 🎯www.tanbircox.blogspot.com
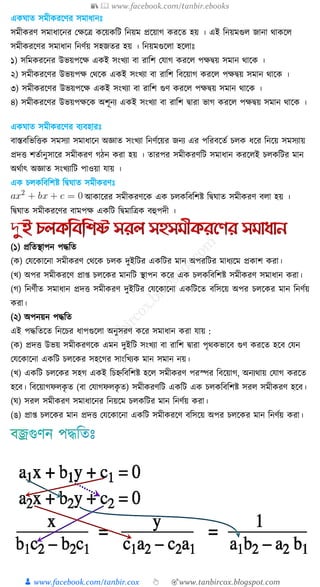
= α+β+γ = -b/a
= αβ+βγ+γα = c/a
αβγ = -d/a
শদ্বঘাে সমীেরণঃ 02
 cbxax এিং এর দুইশি মূে হেঃ
a
acbb
2
42

শদ্বঘাে সমীেরকণর শনশ্চায়ে রুপঃ acb 42

শদ্বঘাে সমীেরকণর গিনঃ 2
x (মূেদকয়র যযাগফে)x+(মূেদকয়র গুনফে)=০
এ ই এ ক্ষ িমজাতীয় দুইত্রি রাত্রির পত্ররমাক্ষণর এ ত্রি অপরত্রির ত গুণ বা ত অংি তা এ ত্রি
ভগ্াংি িারা প্র াি রা োয়, এই ভগ্াংিত্রিক্ষ রাত্রি দুইত্রির অনুপাত বক্ষ । দুইত্রি রাত্রি p ও q
এর অনুপাতক্ষ ত্র খ্া োয় P: 𝑄 =
𝑃
𝑄
িমানুপাতেঃ
েত্রদ চারত্রি রাত্রি এরূপ হয় কে, প্রথম ও ত্রিতীয় রাত্রির অনুপাত তৃতীয় ও চতুথু রাত্রির অনুপাক্ষতর
িমান হয়, তক্ষব ঐ চারত্রি রাত্রি ত্রনক্ষয় এ ত্রি িমানুপাত উতপন্ন হয় । a,b,c,d এরূপ চারত্রি রাত্রি
হক্ষ a : b = c : d
ক্রত্রম িমানুপাতী
a, b, c ক্রত্রম িমানুপাতী ব ক্ষত কবাঝায় a : b = b : c.
a, b, c ক্রত্রম িমানুপাতী হক্ষব েত্রদ এবং ক ব েত্রদ b
2
= ac হয়। ক্রত্রম িমানুপাক্ষতর কেক্ষি
িবগুক্ষ া রাত্রি এ জাতীয় হক্ষত হক্ষব। এক্ষেক্ষি c ক a ও b এর তৃতীয় িমানুপাতী এবং b ক a
ও c এর মর্যিমানুপাতী ব া হয়।
অনুপাক্ষতর রুপান্তর
এখ্াক্ষন অনুপাক্ষতর রাত্রিগুক্ষ া র্নাত্ম িংখ্যা।
(১)a : b = c : d হক্ষ , b : a =d : c [বযস্ত রণ(Invertendo) ]
(২) 𝑎: 𝑏 = 𝑐: 𝑑 হক্ষ , 𝑎: 𝑐 = 𝑏: 𝑑 [এ ান্ত রণ(alternendo)]
(৩) 𝑎: 𝑏 = 𝑐: 𝑑 হক্ষ ,
𝑎+𝑏
𝑏
=
𝑐+𝑑
𝑑
[ কোজন(componendo)]
🎯
𝑎
𝑏
=
𝑐
𝑑
.⋅.
𝑎
𝑏
+ 1 =
𝑐
𝑑
+ 1 [উভয়পক্ষে 1 কোগ ক্ষর] অথুাৎ,
𝑎+𝑏
𝑏
=
𝑐+𝑑
𝑑
(৪) 𝑎: 𝑏 = 𝑐: 𝑑 হক্ষ ,
𝑎−𝑏
𝑏
=
𝑐−𝑑
𝑑
[ ত্রবক্ষয়াজন(dividendo)]
🎯
𝑎
𝑏
=
𝑐
𝑑
⋅.
𝑎
𝑏
− 1 =
𝑐
𝑑
− 1 [উভয়পে কথক্ষ 1 ত্রবক্ষয়াগ ক্ষর] অথুাৎ,
𝑎−𝑏
𝑏
=
𝑐−𝑑
𝑑
(৫)𝑎: 𝑏 = 𝑐: 𝑑 হক্ষ ,
𝑎+𝑏
𝑎−𝑏
=
𝑐+𝑑
𝑐−𝑑
[কোজন-ত্রবক্ষয়াজন(componendo −dividendo)]
(৬)
a
b
=
c
d
=
e
f
=
g
h
হক্ষ , প্রক্ষতয ত্রি অনুপাত =
a+c+e+g
b+d+f+h

20. 📚  www.facebook.com/tanbir.ebooks
👦 www.facebook.com/tanbir.cox 👆 🎯www.tanbircox.blogspot.com
(Series / Progression):
ক্রশমে সমান্তর যারাঃ 1(First Term) +2+3+4+……………………n(Last Term)
এই যারায় সাযারণ অন্তর (Common Difference) =Second term – first Term = 1
 পদসংখ্যা (Number of Terms) =
যিষ পদ−প্রথম পদ
সাযারণ অন্তর
+ 1
 সমশি (Sum of the Series) =
যিষ পদ+প্রথম পদ
2
× পদসংখ্যা =
𝑛(𝑛+1)
2
 গড় (Avarage of the Series) =
যিষ পদ+প্রথম পদ
2
=
𝑛+1
2
a + (a+d) + (a+2d) + (a+3d)+……………………………..n
এখ্াকন যারাশির ,
প্রথম পদ = a
সাযারণ অন্তর d = শদ্বেীয় পদ – প্রথম পদ
পদ সংখ্যা = n
∴ যারার েম n পদ (কিষ পদ) = a +(n−1)d
⇛ n =
যিষ পদ−1
𝑑
−1
যারার n েম পকদর সমশি =
𝑛
2
{2a + (n−1)d}
a + ar + ar2
+ 𝑎𝑟3
… … … . . … . 𝑎𝑟 𝑛−1
এখ্াকন গুকনাত্তর যারাশির,
প্রথম পদ = a
সাযারণ অনুপাে r =
শদ্বেীয় পদ
প্রথম পদ
পদ সংখ্যা = n
যারার n েম পদ = a × rn−1

 r >0 িা 1 অথযাৎ অনুপাে r যনাত্নে পূনয সংখ্যা হকে,
যারার n েম পকদর সমশি 𝑆 𝑛 = 𝑎 ×
𝑟 𝑛−1
𝑟−1
 r < 0 িা 1 অথযাৎ অনুপাে r ঋনাত্নে িা ভগ্াংি (.1 -.9 )সংখ্যা হকে,

21. 📚  www.facebook.com/tanbir.ebooks
👦 www.facebook.com/tanbir.cox 👆 🎯www.tanbircox.blogspot.com
যারার n েম পকদর সমশি 𝑆 𝑛 = 𝑎 ×
1−𝑟 𝑛
1−𝑟
 যখ্ন -1<r<1 হকে , এিং n→∞ হকে
যারার n েম পকদর সমশি 𝑆 𝑛 =
𝑎
1−𝑟
যারার যযাগফে িা সমশি = 𝑆 𝑛
যারাকে পকদর সংখ্যা = n
যারার n েম পদ = যিষ পদ
 1+2+3+4+………………..n
⇛ 𝑆 𝑛 =
𝑛(𝑛+1)
2
 1+3+5+7+……………….
(2𝑛 − 1)
𝑛 েম পদ
যিষ পদ
⇛ 𝑆 𝑛 = (পদসংখ্যা)2
= 𝑛2
 12
+ 22
+ 32
+ 42
+ ⋯ … … … … … . 𝑛2
⇛ 𝑆 𝑛 =
1
6
× n(n-1)(2n+1)
 1 (20) + 22
+ 23
+ 24
+ ⋯ … … … … … … … 2 𝑛−1
⇛ 𝑆 𝑛 = 2 𝑛
− 1
13
+ 23
+ 33
+ 43
+ ⋯ … … … … … … … … … 𝑛3
⇛ 𝑆 𝑛 =
𝑛2(𝑛+1)2
4
= {
𝑛(𝑛+1)
2
}2

22. 📚  www.facebook.com/tanbir.ebooks
👦 www.facebook.com/tanbir.cox 👆 🎯www.tanbircox.blogspot.com

23. 📚  www.facebook.com/tanbir.ebooks
👦 www.facebook.com/tanbir.cox 👆 🎯www.tanbircox.blogspot.com
a কেক্ষ াক্ষনা বাস্তব িংখ্া হক্ষ , n িংখ্য a এর ক্রত্রম গুণ, অথুাৎ, a✕a✕a✕ … … . . ✕a ক an
আ াক্ষর
ক খ্া হয়, কেখ্াক্ষন n র্নাত্ম পূণুিংখ্যা।
a✕a✕a✕ … … . . ✕a (n সংখ্যক a) = an
. এখ্াক্ষন, n --িূচ বা াত , a -- ত্রভত্রত্ত
আবার, ত্রবপরীতক্রক্ষম an
= a✕a✕a✕ … … . . ✕a (n সংখ্যক a)
িূচ শুর্ু র্নাত্ম পূণুিংখ্যাই নয়, ঋণাত্ম পূণুিংখ্যা বা র্নাত্ম ভগ্াংি বা ঋণাত্ম ভগ্াংিও হক্ষত
পাক্ষর।
a ∈ R; m, n ∈ N.
িূি ১। am
✕an
= am+n
িূি ২।
am
an
= {
am−n
যখন m > 𝑛
a
1
n−m যখন n > 𝑚
িূি ৩। (𝑎𝑏) 𝑛
= 𝑎 𝑛
✕ 𝑏 𝑛
িার্ারণভাক্ষব, (𝑎𝑏) 𝑛
= 𝑎𝑏✕ 𝑎𝑏✕ 𝑎𝑏✕… … . ✕ 𝑎𝑏 [n িংখ্য ab এর ক্রত্রম গুণ ]
= (𝑎✕ 𝑎✕ 𝑎✕ … … . ✕ 𝑎)✕(𝑏✕ 𝑏✕ 𝑏✕… … . . ✕ 𝑏)
= 𝑎 𝑛
𝑏 𝑛
িূত্র ৪। (
𝑎
𝑏
) 𝑛
=
𝑎 𝑛
𝑏 𝑛, (𝑏 ≠ 0) =
𝑎✕ 𝑎✕ 𝑎✕……✕ 𝑎
𝑏✕ 𝑏✕ 𝑏✕……✕ 𝑏
=
𝑎 𝑛
𝑏 𝑛
িূি-১ িূচ ত্রবত্রর্ (Index law)
a0
= 1 (a≠0)
a-n
=
1
𝑎 𝑛 (a≠0, n 𝜖 N)মন্তবয:
1
𝑎 𝑛
=
𝑎0
𝑎 𝑛
= 𝑎0−𝑛
= 𝑎−𝑛
িূি ৫। (𝑎 𝑚
) 𝑛
= 𝑎 𝑚𝑛
𝒏 তম মূক্ষ র কেক্ষি,
𝑎
1
𝑛✕ 𝑎
1
𝑛✕ 𝑎
1
𝑛✕ … … . ✕ 𝑎
1
𝑛 [𝑛 িংখ্য 𝑎
1
𝑛 এর ক্রত্রম গুণ]= (
1
𝑎 𝑛)
a এর 𝑛 তম মূ (𝑎)
1
𝑛 = 𝑎
1
𝑛 = √ 𝑎
𝑛
। a এর 𝑛তম মূ ক্ষ √ 𝑎
𝑛
আ াক্ষর ক খ্া হয়।
𝑎 𝑛
= a×a×a×a×a… (n সংখ্যে a এর গুণফে )
 𝑎0
= ( 𝑆𝑜𝑚𝑒𝑡ℎ𝑖𝑛𝑔)0
= 1  𝑎−𝑛
=
1
𝑎 𝑛
 √ 𝑎 = 𝑎
1
2  √ 𝑎
𝑛
= 𝑎
1
𝑛
 √ 𝑎 𝑚𝑛
= ( √ 𝑎
𝑛
)
𝑚
= 𝑎
𝑚
𝑛

24. 📚  www.facebook.com/tanbir.ebooks
👦 www.facebook.com/tanbir.cox 👆 🎯www.tanbircox.blogspot.com
 √ 𝑎
1
𝑛
= 𝑎 𝑛
 √ 𝑎
1
𝑚
1
𝑛
= 𝑎
𝑛
𝑚  √
1
𝑎
1
𝑛
= 𝑎−𝑛
 (𝑎 𝑚
) 𝑛
= 𝑎 𝑚 𝑛
 ( 𝑎 𝑏) 𝑚
= 𝑎 𝑚
. 𝑏 𝑚
 (
𝑎
𝑏
)
𝑚
=
𝑎 𝑚
𝑏 𝑚
 𝑎 𝑚
. 𝑎 𝑛
= 𝑎 𝑚+𝑛

𝑎 𝑚
𝑎 𝑛 িা (𝑎 𝑚
÷ 𝑎 𝑛
) = 𝑎 𝑚−𝑛
 যশদ an
= 𝑎 𝑚
হয় ⇒ ∴ a = √ 𝑎 𝑚𝑛
= 𝑎
𝑚
𝑛
 যশদ a 𝑥
= 𝑎 𝑦
হয় ∴ x =y  যশদ a 𝑚
= 𝑏 𝑚
হয় ∴ a=b

25. 📚  www.facebook.com/tanbir.ebooks
👦 www.facebook.com/tanbir.cox 👆 🎯www.tanbircox.blogspot.com
 log 𝑎 𝑛 যে “ a শভশত্তে েগ n”পড়া হয়।
 শুযু যনাত্নে সংখ্যার েগাশরদম আক । িূনয ও ঋনাত্নে সংখ্যার
েগাশরদম যনই।
 সাযারণ েগাশরদকমর শভশত্ত 10 যরা হয়। log10 𝑀 যিাঝাকে log 𝑀
যে যিাঝায়।
 ax
= 𝑛 হকে x = log 𝑎 𝑛
⇛ x = log 𝑎 𝑛 হকে ax
= 𝑛
log 𝑎𝑛𝑦 𝑏𝑎𝑠𝑒 1 = log 1 = 0 log 𝑎 0 = ∞
log 𝑎 10 = log 10 = 1
log 𝑎 𝑎 = 1
log 𝑎 𝑏 =
1
log 𝑏 𝑎
⇛ log 𝑎 𝑏 × log 𝑏 𝑎 = 1
⇛ log 𝑎 𝑏 × log 𝑏 𝑐 × log 𝑐 𝑎 = 1
log 𝑎 𝑀 = log 𝑏 𝑀 × log 𝑎 𝑏
log 𝑎 𝑀 =
log 𝑏 𝑀
log 𝑏 𝑎
 log 𝑎 𝑀 𝑟
= 𝑟 log 𝑎 𝑀
 log 𝑎( 𝑀𝑁) = log 𝑎 𝑀 + log 𝑎 𝑁
log 𝑎 (
𝑀
𝑁
) = log 𝑎 𝑀 − log 𝑎 𝑁
log 𝑎 √ 𝑚
𝑛
=
1
𝑛
log 𝑎 𝑚
𝑎𝑙𝑜𝑔 𝑥
𝑏
= 𝑏 𝑙𝑜𝑔 𝑥
𝑎
𝑥 𝑦
= 𝑒 𝑦 𝑙𝑜𝑔 𝑒
𝑥

26. 📚  www.facebook.com/tanbir.ebooks
👦 www.facebook.com/tanbir.cox 👆 🎯www.tanbircox.blogspot.com

27. 📚  www.facebook.com/tanbir.ebooks
👦 www.facebook.com/tanbir.cox 👆 🎯www.tanbircox.blogspot.com
প্রাথত্রম আক্ষ াচনা : জযাত্রমত্রত (Initial discussion of geometry)
ইউত্রিক্ষডর স্বী ােুেঃ
১) োর ক াক্ষনা অংি নাই তাই ত্রব্ু ।
২) করখ্ার প্রান্ত ত্রব্ু কনই
৩) োর ক ব দদ ুয আক্ষে ত্র ন্তু প্রস্ত ও উচ্চতা নাই তাই করখ্া ।
৪) কে করখ্ার উপত্ররত্রস্থত ত্রব্ুগুক্ষ া এ ই বরাবক্ষর থাক্ষ তাই ির ক্ষরখ্া ।
৫) োর ক ব দদ ুয ও প্রস্থ আক্ষে তাই ত ।
৬) কে তক্ষ র ির ক্ষরখ্াগুক্ষ া তাাঁর উপর িমভাক্ষব থাক্ষ তাই িমত ।
জযাত্রমত্রত প্রমাণেঃ
জযাত্রমত্রত উপপাক্ষদযর প্রমাক্ষন িার্ারণত ত্রনক্ষনাক্ত র্াপগুক্ষ া থাক্ষ ।
১) িার্ারণ ত্রনবুচন ।
২) ত্রচি ও ত্রবক্ষিষ ত্রনবুচন
৩) প্রক্ষয়াজনীয় অঙ্কক্ষনর ববুণা এবং
৪) প্রমাক্ষণর কেৌত্রক্ত র্াপগুক্ষ ার বণুনা ।
জযাত্রমত্রতেঃ ‘জযা’ অথু ভূ ত্রম, ‘ত্রমত্রত’ অথু পত্ররমাপ । জযাত্রমত্রত হ স্থানত্রভত্রত্ত ত্রবজ্ঞান ।
ত্রব্ুেঃ ত্রব্ুর শুর্ু অবস্থান আক্ষে ত্র ন্তু ক ান মািা কনই ।
করখ্ােঃ ত্রব্ুর চ ার পথক্ষ করখ্া বক্ষ । করখ্া দুই প্র ারেঃ ) ির করখ্া খ্) বক্র করখ্া
নবস্তুেঃ কে বস্তুর দদ ুয, প্রস্থ ও উচ্চতা আক্ষে, তাক্ষ নবস্তু বক্ষ । কেমন, ইি, বই ইতযাত্রদ ।
ক ানেঃ েত্রদ দুইত্রি ির ক্ষরখ্া পরস্পক্ষরর িাক্ষথ ক ান ত্রব্ুক্ষত ত্রমত্র ত হয়, তক্ষব ত্রম ন ত্রব্ুক্ষত ক াণ
উৎপন্ন হয় ।
িত্রন্নত্রহত ক াণেঃ েত্রদ ক ান তক্ষ দুইত্রি ক াক্ষণর এ ই িীষুত্রব্ু হয় এবং ক ানিয় িার্ারণ বাহুর
ত্রবপরীত পাক্ষি অবস্থান ক্ষর, তক্ষব ঐ ক াণিয়ক্ষ িত্রন্নত্রহত ক াণ বক্ষ ।
ত্রবপ্রতীপ ক াণেঃ ক ান ক াক্ষণর বাহুিক্ষয়র ত্রবপরীত রত্রি কে ক াণ দতত্রর ক্ষর, তা ঐ ক াক্ষণর
ত্রবপ্রতীপ ক াণ বক্ষ ।
কগা েঃ দুইত্রি পরস্পর ত্রবপরীত রত্রি তাক্ষদর িার্ারণ প্রান্ত ত্রব্ুক্ষত কে ক াণ উৎপন্ন ক্ষর, তাক্ষ
ির ক াণ বক্ষ ।
িমক্ষ াণেঃ েত্রদ এ ই করখ্ার উপর অবত্রস্থত দুইত্রি িত্রন্নত্রহত ক াণ পরস্পর িমান হয়, তক্ষব ক াণ
দুইত্রি প্রক্ষতয ত্রি িমক্ষ াণ ।
িূক্ষ্মক্ষ াণেঃ এ িমক্ষ াণ কথক্ষ কোি ক াণক্ষ িূক্ষ্মক্ষ াণ বক্ষ ।

28. 📚  www.facebook.com/tanbir.ebooks
👦 www.facebook.com/tanbir.cox 👆 🎯www.tanbircox.blogspot.com
স্থূ ক্ষ াণেঃ এ িমক্ষ াণ কথক্ষ বড় ত্র ন্তু দুই িমক্ষ াণ কথক্ষ কোি ক াণক্ষ স্থূ ক্ষ াণ বক্ষ ।
প্রবৃদ্ধক্ষ াণেঃ দুই িমক্ষ াণ কথক্ষ বড় ত্র ন্তু চার িমক্ষ াণ কথক্ষ কোি ক াণক্ষ প্রবৃদ্ধক্ষ াণ বক্ষ ।
পূর ক্ষ াণেঃ দুইত্রি ক াক্ষণর ত্রডত্রগ্র পত্ররমাক্ষপর িমত্রষ্ট ৯০° হক্ষ ক াণ দুইত্রিক্ষ পরস্পক্ষরর পূর
ক াণ ব া হয় ।
িম্পূর ক াণেঃ দুইত্রি ক াক্ষণর ত্রডত্রগ্র পত্ররমাক্ষপর িমত্রষ্ট ১৮০° হক্ষ , ক াণ দুইত্রিক্ষ িম্পূর ক াণ
ব া হয় ।
িমান্তরা করখ্ােঃ এ ই িমতক্ষ অবত্রস্থত দুত্রি ির করখ্া এক্ষ অপরক্ষ কেদ না রক্ষ ,
তাক্ষদরক্ষ িমান্তরা ির করখ্া বক্ষ ।
কেদ েঃ কে ির ক্ষরখ্া দুই বা তক্ষতাত্রর্ ির ক্ষরখ্াক্ষ কেদ ক্ষর, তাক্ষ কেদ বক্ষ ।
এ ান্তর ক াণেঃ দুইত্রি িমান্তরা ির ক্ষরখ্াক্ষ অপর এ ত্রি ির ক্ষরখ্া ত্রতেু ভাক্ষব কেদ রক্ষ
কেদ ক্ষরখ্ার ত্রবপরীত পাক্ষিু িমান্তরা করখ্া কে ক াণ উৎপন্ন ক্ষর, তাক্ষ এ ান্তর ক াণ বক ।
অনুরুপ ক াণেঃ দুইত্রি িমান্তরা ির ক্ষরখ্াক্ষ অপর এ ত্রি ির ক্ষরখ্া ত্রতেু ভাক্ষব কেদ রক্ষ
কেদ ক্ষরখ্ার এ ই ত্রদক্ষ িমান্তরা করখ্ািক্ষয়র অনুরুপ পাক্ষিু কে ক াণ উৎপন্ন হয়, তাক্ষ
অনুরুপ ক াণ বক্ষ ।
ত্রিভু জেঃ ত্রতনত্রি করখ্াংি িারা আবি কেক্ষির িীমাক্ষরখ্াক্ষ ত্রিভু জ বক্ষ ।
অন্তেঃক্ষ ন্দ্রেঃ ত্রিভু ক্ষজর ক াণিক্ষয়র িমত্রিখ্ন্ড গুক্ষ া িমত্রব্ু ।িই ত্রব্ু ত্রিভু ক্ষজর অন্তেঃক্ষ ন্দ্র।
পত্ররক্ষ ন্দ্রেঃ ত্রিভু ক্ষজর বাহুিক্ষয়র ম্বত্রিখ্ন্ড িয় িমত্রব্ু। িই ত্রব্ু ত্রিভু ক্ষজর পত্ররক্ষ ন্দ্র।
ভরক্ষ ন্দ্রেঃ ত্রিভু ক্ষজর ক াণ এ ত্রি িীষুত্রব্ু এবং তার ত্রবপরীত বাহুর মর্যত্রব্ুর িংক্ষোজ
ির ক্ষরখ্াক্ষ মর্যমা বক্ষ । ত্রিভু ক্ষজর মর্যমািয় িমত্রব্ু । িই ত্রব্ু ত্রিভু ক্ষজর ভরক্ষ ন্দ্র।
ম্বত্রব্ুেঃ ত্রিভু ক্ষজর িীষুিয় হক্ষত ত্রবপরীত বাহুর উপর অত্রঙ্কত ম্বিয় িমত্রব্ু। িই ত্রব্ু ত্রিভু ক্ষজর
ম্বত্রব্ু।
িমবাহু ত্রিভু জেঃ কে ত্রিভু ক্ষজর ত্রতনত্রি বাহু িমান, তাক্ষ িমবাহু ত্রিভু জ বক্ষ ।
িমত্রিবাহু ত্রিভু জেঃ কে ত্রিভু ক্ষজর দুইত্রি বাহু িমান, তাক্ষ িমত্রিবাহু ত্রিভু জ ব া হয় ।
ত্রবষমবাহু ত্রিভু জেঃ কে ত্রিভু ক্ষজর ত্রতনত্রি বাহুর দদ ুযই ত্রভন্ন ত্রভন্ন, তাক্ষ ত্রবষমবাহু ত্রিভু জ ব া হয় ।
িমক্ষ াণী ত্রিভু জেঃ কে ত্রিভু ক্ষজর এ ত্রি ক াণ িমক্ষ াণ, তাক্ষ িমক্ষ াণী ত্রিভু জ ব া হয় ।
িূক্ষ্মক্ষ াণী ত্রিভু জেঃ কে ত্রিভু ক্ষজর ত্রতনত্রি ক াণই িূক্ষ্মক্ষ াণ, তাক্ষ িূক্ষ্মক্ষ াণী ত্রিভু জ বক্ষ ।
স্থু ক্ষ াণী ত্রিভু জেঃ কে ত্রিভু ক্ষজর এ ত্রি ক াণ স্থু ক্ষ াণ, তাক্ষ স্থু ক্ষ াণী ত্রিভু জ বক্ষ ।
িবুিমেঃ দুইত্রি কেি িবুিম হক্ষব েত্রদ এ ত্রি কেি অনযত্রির িাক্ষথ িবুক্ষতাভাক্ষব ত্রমক্ষ োয় । িবুিম
ব ক্ষত আ ার ও আ ৃ ত্রত িমান বুঝায় ।
িদৃিক্ষ াণী ত্রিভু জেঃ দুইত্রি ত্রিভু ক্ষজর এ ত্রির ত্রতনত্রি ক াণ অপরত্রির ত্রতনত্রি ক াক্ষণর িমান হক্ষ ,
ত্রিভু জ দুইত্রিক্ষ িদৃিক্ষ াণী ব া হয় ।
চতু ভু ুজেঃ চারত্রি ির ক্ষরখ্া িারা িীমাবদ্ধ কেিক্ষ চতুভু ুজ বক্ষ ।
ণুেঃ চতু ভু ুক্ষজর ত্রবপরীত ক ৌত্রণ িীক্ষষুর িংক্ষোজগ ির ক্ষরখ্াক্ষ ণু বক্ষ ।
িামন্তত্রর েঃ চতুভু ুক্ষজর ত্রবপরীত বাহুগুক্ষ া িমান্তরা হক্ষ তাক্ষ িামন্তত্রর বক্ষ ।
আয়তক্ষেিেঃ িামন্তত্ররক্ষ র এ ত্রি ক ান িমক্ষ াণ হক্ষ তাক্ষ আয়তক্ষেি বক্ষ ।
বগুেঃ আয়তক্ষেক্ষির দুত্রি িত্রন্নত্রহত বাহু িমান হক্ষ তাক্ষ বগু বক্ষ ।
রম্বিেঃ িামন্তত্ররক্ষ র দুত্রি িত্রন্নত্রহত বাহু িমান হক্ষ তাক্ষ রম্বি বক্ষ ।
ট্রাত্রপত্রজয়ামেঃ কে চতুভু ুক্ষজর ক ব মাি দুইত্রি বাহু িমান্তরা , তাক্ষ ট্রাত্রপত্রজয়াম বক্ষ ।
স্পিু েঃ এ ত্রি বৃত্ত ও এ ত্রি ির ক্ষরখ্ার েত্রদ এ ত্রি ও ক ব কেদত্রব্ু থাক্ষ তক্ষব করখ্াত্রিক্ষ
বৃত্তত্রির এ ত্রি স্পিু ব া হয় ।

29. 📚  www.facebook.com/tanbir.ebooks
👦 www.facebook.com/tanbir.cox 👆 🎯www.tanbircox.blogspot.com
িার্ারণ স্পিু েঃ এ ত্রি ির ক্ষরখ্ার েত্রদ দুইত্রি বৃক্ষত্তর স্পিু হয়, তক্ষব বৃত্ত দুইত্রির এ ত্রি
িার্ারণ স্পিু ব া হয় ।
আয়ত্রত নবস্তুেঃ ত্রতন কজাড়া িমান্তরা আয়তা ার িমত বা পৃষ্ট িারা আবদ্ধ নবস্তুক্ষ
আয়ত্রত নবস্তু বক্ষ ।
ন েঃ আয়তা ার নবস্তুর দদ ুয, প্রস্থ ও উচ্চতা িমান হক্ষ , তাক্ষ ন বক্ষ ।
ক াণ েঃ ক ান িমক্ষ াণী ত্রিভু ক্ষজ িমক্ষ াণ িং গ্ কে ক ান এ ত্রি বাহুক্ষ ত্রস্থর করক্ষখ্ ঐ বাহুর
চতু ত্রদুক্ষ ত্রিভু জত্রিক্ষ ুরাক্ষ কে নবস্তু উৎপন্ন হয় তাক্ষ িমবৃত্তভু ত্রম ক াণ বক্ষ ।
ত্রিত্র ন্ডার বা কব ুনেঃ এ ত্রি আয়তক্ষেক্ষির কে ক ান এ ত্রি বাহুক্ষ ত্রস্থর করক্ষখ্ ঐ বাহুর চতুত্রদুক্ষ
আয়তক্ষেিত্রিক্ষ ুরাক্ষ কে নবস্তু উৎপন্ন হয় তাক্ষ িমবৃত্তভু ত্রম কব ুন বক্ষ ।
কগা েঃ ক ান অর্ুবৃক্ষত্তর বযািক্ষ অে র্ক্ষর অর্ুবৃত্তত্রিক্ষ ঐ বযাক্ষির চারত্রদক্ষ ুরাক্ষ কে নবস্তু
উৎপন্ন হয়, তাক্ষ কগা বক্ষ ।
বৃত্ত :ত্রনত্রদুষ্ট ত্রব্ু কথক্ষ িমদূরত্ব বজায় করক্ষখ্ ক াক্ষনা ত্রব্ু কে আবদ্ধ পথ ত্রচত্রিত ক্ষর তাই বৃত্ত।
বৃক্ষত্তর জযা ও বযাি: বৃক্ষত্তর দুত্রি ত্রভন্ন ত্রব্ুর িংক্ষোজ করখ্াংি বৃত্তত্রির জযা। বৃক্ষত্তর জযা েত্রদ ক ন্দ্র
ত্রদক্ষয় োয় তক্ষব তাক্ষ বৃক্ষত্তর বযাি ব া হয়।
বৃত্তচাপেঃ বৃক্ষত্তর কেক্ষ াক্ষনা দুইত্রি ত্রব্ুর মক্ষর্যর পত্ররত্রর্র অংিক্ষ চাপ বক্ষ ।
বৃত্তস্থ ক াণেঃ এ ত্রি ক াক্ষণর িীষুত্রব্ু ক াক্ষনা বৃক্ষত্তর এ ত্রি ত্রব্ু হক্ষ এবং ক ানত্রির প্রক্ষতয
বাহুক্ষত িীষুত্রব্ু োড়াও বৃক্ষত্তর এ ত্রি ত্রব্ু থা ক্ষ ত্রন্তক্ষ এ ত্রি বৃত্তস্থ ক াণ বা বৃক্ষত্ত
অন্তরত্র ত্রখ্ত ক াণ ব া হয় ।
ক ন্দ্রস্থ ক াণেঃ এ ত্রি ক াক্ষণর িীষুত্রব্ু ক াক্ষনা বৃক্ষত্তর ক ক্ষন্দ্র অবত্রস্থত হক্ষ , ক াণত্রিক্ষ ঐ বৃক্ষত্তর
এ ত্রি ক ন্দ্রস্থ ক াণ ব া হয় এবং ক াণত্রি বৃক্ষত্ত কে চাপ ক্ষর কিই চাক্ষপর ওপর তা দণ্ডায়মান
ব া হয় ।
বৃক্ষত্তর কেদ ও স্পিু েঃ িমত স্থ এ ত্রি বৃত্ত ও এ ত্রি ির ক্ষরখ্ার েত্রদ দুইত্রি কেদত্রব্ু থাক্ষ
তক্ষব করখ্াত্রিক্ষ বৃত্তত্রির এ ত্রি কেদ ব া হয় এবং েত্রদ এ ত্রি এবং ক ব এ ত্রি িার্ারন ত্রব্ু
থাক্ষ তক্ষব করখ্াত্রিক্ষ বৃত্তত্রির এ ত্রি স্পিু ব া হয়।
িার্ারণ স্পিু েঃ এ ত্রি ির ক্ষরখ্া েত্রদ দুত্রি বৃক্ষত্তর স্পিু তক্ষব তাক্ষ বৃত্ত দুত্রির এ ত্রি িার্ারন
স্পিু বক্ষ ।
অত্রতভু জেঃ িমক্ষ াণী ত্রিভু ক্ষজর বৃহত্তম বাহু ো িম ক্ষনর ত্রবপরীত বাহু ।
ত্রবপরীত বাহুেঃ ো হক্ষ া প্রদত্ত ক াক্ষণর িরািত্রর ত্রবপরীত ত্রদক্ষ র বাহু ।
িত্রন্নত্রহত বাহুেঃ ো প্রদত্ত ক াণ িৃত্রষ্ট ারী এ ত্রি করখ্াংি ।
ভু -ক্ষরখ্া, ঊর্ধ্ুক্ষরখ্া এবং উল্লম্বত েঃ
ভু ক্ষরখ্া হক্ষে ভু ত্রমতক্ষ অবত্রস্থত কজ ন ির ক্ষরখ্া। ঊর্ধ্ুক্ষরখ্া হক্ষে ভু ত্রমতক্ষ র উপর ম্ব
ির ক্ষরখ্া। ভু ত্রমতক্ষ র উপর ম্বভাক্ষব অবত্রস্থত পরস্পরক্ষেত্রদ ভু -ক্ষরখ্া ও ঊর্ধ্ুক্ষরখ্া এ ত্রি ত
ত্রনক্ষদুি ক্ষর জাক্ষ উল্লম্ব ত বক্ষ ।
উন্নত্রত ক াণ: ভু তক্ষ র উপক্ষরর ক ান ত্রব্ু ভু ত্রমর িমান্তরা করখ্ার িাক্ষথ জযা ক াণ উৎপন্ন ক্ষর
তাক্ষ উন্নত্রত ক াণ বক্ষ ,
অবনত্রত ক াণেঃ ভু তক্ষ র ত্রনক্ষচর ক ান ত্রব্ু ভু ত্রমর িমান্তরা করখ্ার িাক্ষথ জযা ক াণ উৎপন্ন ক্ষর
তাক্ষ অবনত্রত ক াণ বক্ষ .

30. 📚  www.facebook.com/tanbir.ebooks
👦 www.facebook.com/tanbir.cox 👆 🎯www.tanbircox.blogspot.com
🎯 ১) এ ত্রি রত্রির প্রাণ-ত্রব্ুক্ষত অপর এ ত্রি ির ক্ষরখ্া ত্রমত্র ত হক্ষ , কে দুইত্রি িত্রন্নত্রহত ক াণ উৎপন্ন
হয়, এক্ষদর িমত্রষ্ট দুই িমক্ষ াণ।
🎯 ২) দুইত্রি িত্রন্নত্রহত ক াক্ষণর িমত্রষ্ট দুই িমক্ষ াক্ষণর িমান হক্ষ , এক্ষদর বত্রহেঃস্থ বাহুিয় এ ই ির ক্ষরখ্ায়
অবত্রস্থত।
🎯 ৩) দুইত্রি ির ক্ষরখ্া পরস্পর কেদ রক্ষ উৎপন্ন ত্রবপ্রতীপ ক াণগুক্ষ া পরস্পর িমান।
🎯 ৪) এ ত্রি ির ক্ষরখ্া অপর দুইত্রি িমান্তরা ির ক্ষরখ্াক্ষ কেদ রক্ষ
) এ ান্তর ক াণদুইত্রি িমান হক্ষব
খ্) অনুরূপ ক াণদুইত্রি িমান হক্ষব এবং
গ) কেদক্ষ র এ ই পাক্ষির অন্তেঃস্থ ক াণ দুইত্রির িমত্রষ্ট দুই িমক্ষ াণ হক্ষব।
🎯 ৫) দুইত্রি ির ক্ষরখ্াক্ষ অপর এ ত্রি ির ক্ষরখ্া কেদ রক্ষ , েত্রদ
) এ ান্তর ক াণগুক্ষ া িমান হয়, অথবা
খ্) অনুরূপ ক াণগুক্ষ া িমান হয়, অথবা
গ) কেদক্ষ র এ ই পাক্ষির অন্তেঃস্থ ক াণ দুইত্রির িমত্রষ্ট দুই িমক্ষ াক্ষণর িমান হয়, তক্ষব ঐ করখ্া দুইত্রি
িমান্তরা হক্ষব।
🎯 ৬) কেিব করখ্া এ ই ির ক্ষরখ্ার িমান্তরা তারা পরস্পর িমান্তরা ।
🎯 ৭) েত্রদ দুইত্রি ত্রিভু ক্ষজর এ ত্রির দুই বাহু েথাক্রক্ষম অপরত্রির দুই বাহুর িমান হয় এবং বাহু দুইত্রির
অন্তভু ুক্ত ক াণ দুইত্রি পরস্পর িমান হয়, তক্ষব ত্রিভু জ দুইত্রি িবুিম হক্ষব।
🎯 ৮) েত্রদ ক ান ত্রিভু ক্ষজর দুইত্রি বাহু পরস্পর িমান হয়, তকব এক্ষদর ত্রবপরীত ক াণ দুইত্রিও পরস্পর
িমান হক্ষব।
🎯 ৯) েত্রদ ক ান ত্রিভু ক্ষজর দুইত্রি ক াণ পরস্পর িমান হয়, তক্ষব এক্ষদর ত্রবপরীত বাহুিয়ও পরস্পর িমান
হক্ষব।
🎯 ১০) েত্রদ এ ত্রি ত্রিভু ক্ষজর ত্রতন বাহু অপর এ ত্রি ত্রিভু ক্ষজর ত্রতন বাহুর িমান হয়, তক্ষব ত্রিভু জ দুইত্রি
িবুিম হক্ষব।
🎯 ১১) ক ান ত্রিভু ক্ষজর এ ত্রি বাহু অপর এ ত্রি বাহু অক্ষপো বৃহত্তর হক্ষ , বৃহত্তর বাহুর ত্রবপরীত ক াণ
েু দ্রতর বাহুর ত্রবপরীত ক াণ অক্ষপো বৃহত্তর হক্ষব।
🎯 ১২) ক ান ত্রিভু ক্ষজর এ ত্রি ক াণ অপর এ ত্রি ক াণ অক্ষপো বৃহত্তর হক্ষ , বৃহত্তর ক াক্ষণর ত্রবপরীত
বাহু েু দ্রতর ক াক্ষণর ত্রবপরীত বাহু অক্ষপো বৃহত্তর হক্ষব।
🎯 ১৩) ত্রিভু ক্ষজর কেক্ষ াক্ষনা দুই বাহুর িমত্রষ্ট, তার তৃতীয় বাহু অক্ষপো বৃহত্তর।
🎯 ১৪) ক ান ির ক্ষরখ্ার বত্রহেঃস্থ ক ান ত্রব্ু কথক্ষ উক্ত ির ক্ষরখ্া পেুন্ত- েতগুক্ষ া করখ্াংি িানা োয়
তন্মক্ষর্য ম্ব করখ্াংিত্রি েু দ্রতম।
🎯 ১৫) ত্রিভু ক্ষজর ত্রতন ক াক্ষণর িমত্রষ্ট দুই িমক্ষ াক্ষণর িমান।
🎯 ১৬) েত্রদ এ ত্রি ত্রিভু ক্ষজর দুইত্রি ক াণ ও এ ত্রি বাহু েথাক্রক্ষম অপর এ ত্রি ত্রিভু ক্ষজর দুইত্রি ক াণ এবং
অনুরূপ বাহুর িমান হয়, তক্ষব ত্রিভু জ দুইত্রি িবুিম হক্ষব।
🎯 ১৭) দুইত্রি িমক্ষ াণী ত্রিভু ক্ষজর অত্রতভু জিয় িমান হক্ষ এবং এ ত্রির এ বাহু অপরত্রির অপর এ
বাহুর িমান হক্ষ ত্রিভু জিয় িবুিম হক্ষব।
✐ ২.১) ত্রিভু ক্ষজর এ ত্রি বাহু বত্রর্ুত রক্ষ কে বত্রহেঃস্থ ক াণ উৎপন্ন হয় তা ত্রবপরীত অন্তেঃস্থ ক াণিক্ষয়র
িমত্রষ্টর িমান।

31. 📚  www.facebook.com/tanbir.ebooks
👦 www.facebook.com/tanbir.cox 👆 🎯www.tanbircox.blogspot.com
✐ ২.২) ত্রিভু ক্ষজর এ ত্রি বাহু বত্রর্ুত রক্ষ উৎপন্ন বত্রহেঃস্থ ক াণত্রি অন্তেঃস্থ ত্রবপরীত ক াণিক্ষয়র
প্রক্ষতয ত্রি অক্ষপো বৃহত্তর হক্ষব।
🎯 ১৮) চতুভু ুক্ষজর দুইত্রি ত্রবপরীত বাহু িমান ও িমান্তরা হক্ষ , অপর বাহু দুইত্রিও িমান ও িমান্তরা
হক্ষব।
🎯 ১৯) িামান্তত্ররক্ষ র ত্রবপরীত বাহুগুক্ষ া ও ক াণগুক্ষ া পরস্পর িমান এবং প্রক্ষতয ণু িামান্তত্রর ক্ষ
দুইত্রি িবুিম ত্রিভু ক্ষজ ত্রবভক্ত ক্ষর।
✐ ২.৩) িামান্তত্ররক্ষ র ণুিয় পরস্পরক্ষ িমত্রিখ্ত্রণ্ডত কর।
✐ ২.৪) রম্বক্ষির ণুিয় পরস্পরক্ষ িমক্ষ াক্ষণ িমত্রিখ্ত্রণ্ডত ক্ষর।
✐ ২.৫) ত্রিভু ক্ষজর কেক্ষ ান দুই বাহুর মর্যত্রব্ুর িংক্ষোজ করখ্াংি তৃতীয় বাহুর িমান্তরা এবং দদক্ষ ুয
তার অক্ষর্ু ।
🎯 ২০) এ ত্রি ত্রিভু জক্ষেি ও এ ত্রি িামান্তত্রর ক্ষেি এ ই ভূ ত্রমর উপর এবং এ ই িমান্তরা
করখ্ােুগক্ষ র মক্ষর্য অবত্রস্থত হক্ষ , ত্রিভু জক্ষেিত্রির কেিফ িামান্তত্রর কেিত্রির কেিফক্ষ র অক্ষর্ু হক্ষব।
🎯 ২১) এ ই ভূ ত্রমর উপর এবং এ ই িমান্তরা করখ্ােুগক্ষ র মক্ষর্য অবত্রস্থত ি ত্রিভু জক্ষেক্ষির
কেিফ িমান।
🎯 ২২) এ ই ভূ ত্রমর উপর এবং এ ই পাক্ষি অবত্রস্থত িমান কেিফ ত্রবত্রিষ্ট ি ত্রিভু জক্ষেি এ ই
িমান্তরা করখ্ােুগক্ষ র মক্ষর্য অবত্রস্থত হক্ষব।
🎯 ২২ ( ): এ ই ভূ ত্রমর উপর এবং এ ই িমান্তরা করখ্ােুগক্ষ র মক্ষর্য অবত্রস্থত িামান্তত্রর ক্ষেিিমূক্ষহর
কেিফ িমান।
🎯 ২২ (খ্): িমান িমান ভূ ত্রমর উপর এবং এ ই িমান্তরা করখ্ােুগক্ষ র মক্ষর্য অবত্রস্থত
িামান্তত্রর ক্ষেিিমূক্ষহর কেিফ িমান।
🎯 ২৩) এ ত্রি িমক্ষ াণী ত্রিভু ক্ষজর অত্রতভূ ক্ষজর উপর অত্রঙ্কত বগুক্ষেক্ষির কেিফ অপর দুই বাহুর উপর
অত্রঙ্কত বগুক্ষেিিক্ষয়র কেিফক্ষ র িমত্রষ্টর িমান।
✐ ∆ABC এ, A = এ িমক্ষ াণ এবং AD, BC বাহুর উপর D ত্রব্ুক্ষত ম্ব হক্ষ , AB২ = BC.BD
এবং AC২ = BC.DC।
🎯 ২৪) েত্রদ ক ান ত্রিভু ক্ষজর এ ত্রি বাহুর উপর অত্রঙ্কত বগুক্ষেক্ষির কেিফ অপর দুইত্রি বাহুর উপর
অত্রঙ্কত বগুক্ষেিিক্ষয়র কেিফক্ষ র িমত্রষ্টর িমান হয়, তক্ষব কিক্ষষাক্ত বাহুিক্ষয়র অন্তভু ুক্ত ক াণত্রি িমক্ষ াণ
হক্ষব।
🎯 ২৫) ত্রিভু ক্ষজর ক ান এ বাহুর িমান্তরা কেক্ষ ান করখ্াংি তার অপর দুই বাহুক্ষ বা তাক্ষদর
বত্রর্ুতাংিিয়ক্ষ িমান অনুপাক্ষত ত্রবভক্ত ক্ষর।
🎯 ২৬) ক ান করখ্াংি এ ত্রি ত্রিভু ক্ষজর দুই বাহুক্ষ বা তাক্ষদর বত্রর্ুতাংিিয়ক্ষ িমান অনুপাক্ষত ত্রবভক্ত
রক্ষ , উক্ত করখ্াংি ত্রিভু জত্রির তৃতীয় বাহুর িমান্তরা হক্ষব।
🎯 ২৭) দুইত্রি ত্রিভু জ িদৃিক্ষ াণী হক্ষ তাক্ষদর অনুরূপ বাহুগুক্ষ ার অনুপাত িমান হক্ষব।

32. 📚  www.facebook.com/tanbir.ebooks
👦 www.facebook.com/tanbir.cox 👆 🎯www.tanbircox.blogspot.com
🎯 ২৮) দুইত্রি ত্রিভু ক্ষজর বাহুগুক্ষ া িমানুপাত্রত হক্ষ ত্রিভু জিয় িদৃিক্ষ াণী এবং তাক্ষদর অনুরূপ বাহুর
ত্রবপরীত ক াণগুক্ষ া পরস্পর িমান হক্ষব।
🎯 ২৯) দুইত্রি ত্রিভু ক্ষজর মক্ষর্য এ ত্রির এ ক াণ অপরত্রির এ ক াক্ষণর িমান হক্ষ এবং িমান িমান
ক াণ িং গ্ বাহুগুক্ষ া িমানুপাত্রত হক্ষ , ত্রিভু জিয় িদৃি হক্ষব।
🎯 ৩০) দুইত্রি িদৃি ত্রিভু ক্ষজর কেিফ িক্ষয়র অনুপাত তাক্ষদর কেক্ষ ান দুই বাহুর উপর অত্রঙ্কত
বগুক্ষেিিক্ষয়র কেিফক্ষ র অনুপাক্ষতর িমান।
🎯 ৩১) দুইত্রি ত্রনত্রদুষ্ট ত্রব্ু কথক্ষ িমদূরবতুী ক ান ত্রব্ুর িঞ্চারপথ উক্ত ত্রব্ুিক্ষয়র িংক্ষোজ করখ্াংক্ষির
ম্বিমত্রিখ্ণ্ড ।
🎯 ৩২) পরস্পরক্ষেদী দুইত্রি ির ক্ষরখ্া কথক্ষ িমদূরবতুী ক ান ত্রব্ুর িঞ্চারপথ উক্ত ত্রনত্রদুষ্ট করখ্া দুইত্রির
অন্তভু ুক্ত ক াণিক্ষয়র িমত্রিখ্ণ্ড িয় হক্ষব।
বৃক্ষত্তর জযা ও বযাি
🎯 ৩৩) বৃক্ষত্তর বযাি ত্রভন্ন ক ান জযা এর মর্যত্রব্ু ও ক ক্ষন্দ্রর িংক্ষোজ করখ্াংি ঐ জযা এর উপর ম্ব।
🎯 ৩৪) বৃক্ষত্তর ক ন্দ্র কথক্ষ বযাি ত্রভন্ন অনয ক ান জযা-এর উপর অত্রঙ্কত ম্ব ঐ জযাক্ষ িমত্রিখ্ত্রণ্ডত ক্ষর।
✐ ১) বৃক্ষত্তর কেক্ষ ান জযা এর ম্ব-ত্রিখ্ণ্ড ক ন্দ্রগামী।
✐ ২) কেক্ষ ান ির ক্ষরখ্া এ ত্রি বৃত্তক্ষ দুইক্ষয়র অত্রর্ ত্রব্ুক্ষত কেদ রক্ষত পাক্ষর না।
✐ ৩) দুইত্রি পরস্পরক্ষেদী বৃক্ষত্তর ক ন্দ্রিক্ষয়র িংক্ষোজ করখ্াংি তাক্ষদর িার্ারণ জযা-ক িমক্ষ াক্ষণ
িমত্রিখ্ত্রণ্ডত ক্ষর।
🎯 ৩৫) বৃক্ষত্তর িমান িমান জযা ক ন্দ্র কথক্ষ িমদূরবতুী।
🎯 ৩৬) বৃক্ষত্তর ক ন্দ্র কথক্ষ িমদূরবতুী ি জযা পরস্পর িমান।
✐ উদাহরণ ১০.১। বৃক্ষত্তর দুইত্রি জযা-এর মক্ষর্য ক ক্ষন্দ্রর ত্রন িতম জযা-ত্রি অপর জযা অক্ষপো বৃহত্তর।
✐ উদাহরণ ১০.২। বৃক্ষত্তর বযািই বৃহত্তম জযা।
🎯 ৩৭) বৃক্ষত্তর এ ই চাক্ষপর উপর দণ্ডায়মান বৃত্তেঃস্থ ক াণ ক ন্দ্রস্থ ক াক্ষণর অক্ষর্ু ।
🎯 ৩৮) বৃক্ষত্তর এ ই চাক্ষপর উপর দণ্ডায়মান বৃত্তেঃস্থ ক াণগুক্ষ া পরস্পর িমান।
🎯 ৩৯) দুইত্রি ত্রব্ুর িংক্ষোজ করখ্াংি তার এ ই পাক্ষি অপর দুই ত্রব্ুক্ষত িমান ক াণ উৎপন্ন রক্ষ ,
ত্রব্ু চারত্রি িমবৃত্ত হক্ষব।
✐ এ ই ভূ ত্রমর উপর এবং তার এ ই পাক্ষি অবত্রস্থত িমান ত্রিরেঃক্ষ াণত্রবত্রিষ্ট ত্রিভু জগুক্ষ ার িীষুত্রব্ুিমূহ
িমবৃত্ত হক্ষব।
🎯 ৪০) অর্ুবৃত্তেঃস্থ ক াণ এ িমক্ষ াণ।
✐ ১) ক ান বৃক্ষত্তর ( ) অত্রর্চাক্ষপ অন্তত্র ুত্রখ্ত ক াণ িূক্ষ্মক্ষ াণ এবং (খ্) উপচাক্ষপ অন্তত্র ুত্রখ্ত ক াণ
স্থূ ক্ষ াণ।
✐ ২) িমক্ষ াণী ত্রিভু ক্ষজর অত্রতভু জক্ষ বযাি র্ক্ষর বৃত্ত অঙ্কন রক্ষ তা িমক্ষ ৌত্রণ িীষুত্রব্ু ত্রদক্ষয় োক্ষব।
🎯 ৪১) বৃক্ষত্ত অন্তত্র ুত্রখ্ত চতু ভু ুক্ষজর কেক্ষ ান দুইত্রি ত্রবপরীত ক াক্ষণর িমত্রষ্ট দুই িমক্ষ াণ।

33. 📚  www.facebook.com/tanbir.ebooks
👦 www.facebook.com/tanbir.cox 👆 🎯www.tanbircox.blogspot.com
✐ ১) বৃক্ষত্ত অন্তত্র ুত্রখ্ত চতুভু ুক্ষজর এ ত্রি বাহু বত্রর্ুত রক্ষ কে বত্রহেঃস্থ ক াণ উৎপন্ন হয় তা ত্রবপরীত
অন্তেঃস্থ ক াক্ষণর িমান।
✐ ২) বৃক্ষত্ত অন্তত্র ুত্রখ্ত িামান্তত্রর এ ত্রি আয়তক্ষেি।
🎯 ৪২) ক ান চতু ভু ুক্ষজর দুইত্রি ত্রবপরীত ক াণ িম্পূর হক্ষ তার িীষুত্রব্ু চারত্রি িমবৃত্ত হয়।
🎯 ৪৩) িমান িমান বৃত্তচাক্ষপর উপর দণ্ডায়মান ক ন্দ্রস্থ বা বৃত্তেঃস্থ ক াণগুক্ষ া িমান।
🎯 ৪৪) িমান িমান বৃক্ষত্ত কে ি চাক্ষপর উপর দণ্ডায়মান ক ন্দ্রস্থ বা বৃত্তেঃস্থ ক াণগুক্ষ া িমান, কি ি
চাপ িমান।
🎯 ৪৫) িমান িমান বৃক্ষত্ত িমান িমান জযা িমান িমান চাপ ত্রেন্ন ক্ষর।
🎯 ৪৬) িমান িমান বৃক্ষত্ত কে ি জযা িমান িমান চাপ ত্রেন্ন ক্ষর, তারা পরস্পর িমান।
🎯 ৪৭) বৃক্ষত্তর কেক্ষ ান ত্রব্ুক্ষত অত্রঙ্কত স্পিু স্পিুত্রব্ুগামী বযািাক্ষর্ুর উপর ম্ব।
✐ ১) বৃক্ষত্তর ক ান ত্রব্ুক্ষত এ ত্রি মাি স্পিু অঙ্কন রা োয়।
✐ ২) স্পিুত্রব্ুক্ষত স্পিুক্ষ র উপর অত্রঙ্কত ম্ব ক ন্দ্রগামী।
✐ ৩) বৃক্ষত্তর ক ন্দ্র কথক্ষ এর ক ান স্পিুক্ষ র উপর অত্রঙ্কত ম্ব স্পিুত্রব্ু ত্রদক্ষয় োয়।
✐ ৪) বৃক্ষত্তর ক ান ত্রব্ুগামী বযািাক্ষর্ুর উপর অত্রঙ্কত ম্ব উক্ত ত্রব্ুক্ষত বৃত্তত্রির স্পিু হয়।
🎯 ৪৮) বৃক্ষত্তর বত্রহেঃস্থ ক ান ত্রব্ু কথক্ষ বৃক্ষত্ত দুইত্রি স্পিু িানক্ষ , ঐ ত্রব্ু কথক্ষ স্পিু ত্রব্ুিক্ষয়র দূরত্ব
িমান হক্ষব।
🎯 ৪৯) দুইত্রি বৃত্ত পরস্পর স্পিু রক্ষ , তাক্ষদও ক ন্দ্রিয় ও স্পিু ত্রব্ু িমক্ষরখ্ হক্ষব।
✐ ১) দুইত্রি বৃত্ত পরস্পরক্ষ বত্রহেঃস্পিু রক্ষ , ক ন্দ্রিক্ষয়র দূরত্ব বৃত্তিক্ষয়র বযািাক্ষর্ুর িমত্রষ্টর িমান হক্ষব।
✐ ২) দুইত্রি বৃত্ত পরস্পরক্ষ অন্তেঃস্পিু রক্ষ , ক ন্দ্রিক্ষয়র দূরত্ব বৃত্তিক্ষয়র বযািাক্ষর্ুর অন্তক্ষরর িমান হক্ষব।
✐ ৩) দুইত্রি বৃত্ত পরস্পরক্ষ বত্রহেঃস্পিু রক্ষ , স্পিুত্রব্ু োড়া প্রক্ষতয বৃক্ষত্তর অনয ি ত্রব্ু অপর
বৃক্ষত্তর বাইক্ষর থা ক্ষব।
✐ ৪) দুইত্রি বৃত্ত পরস্পরক্ষ অন্তেঃস্পিু রক্ষ , স্পিুত্রব্ু োড়া কোি বৃক্ষত্তর অনয ি ত্রব্ু বড় বৃত্তত্রির
অভযন্তক্ষর থা ক্ষব।
🎯 ৫০) বৃক্ষত্তর উপরস্থ ক ান ত্রব্ুক্ষত অত্রঙ্কত স্পিু এবং ঐ ত্রব্ুগামী কেক্ষ ান জযা-এর অন্তগুত ক াণ
তার এ ান্তর বৃত্তাংক্ষির কেক্ষ ান ক াক্ষণর িমান।
✐ ১) িমত্রিবাহু ত্রিভু ক্ষজর ত্রিরেঃক্ষ াক্ষণর িমত্রিখ্ণ্ড ভূ ত্রমক্ষ ও িম-ত্রিখ্ত্রণ্ডত ক্ষর এবং ভূ ত্রমর উপর ম্ব
হয়।
✐ ২) িমবাহু ত্রিভু ক্ষজর বাহুগুক্ষ ার মর্যত্রব্ুিমূহ কোগ রক্ষ কে ত্রিভু জ উৎপন্ন হয়, তা িমবাহু হক্ষব।
✐ ৩) িমবাহু ত্রিভু ক্ষজর মর্যমা ত্রতনত্রি পরস্পর িমান।
✐ ৪) ত্রিভু ক্ষজর কেক্ষ ান দুইত্রি বত্রহেঃস্থ ক াক্ষণর িমত্রষ্ট দুই িমক্ষ াণ অক্ষপো বৃহত্তর।
✐ ৭) ত্রিভু ক্ষজর মর্যমািক্ষয়র িমত্রষ্ট তার পত্ররিীমা অক্ষপো েু দ্রতর।
✐ ১৫) ত্রিভু ক্ষজর কেক্ষ ান দুই বাহুর অন্তর তার তৃতীয় বাহু অক্ষপো েু দ্রতর।

34. 📚  www.facebook.com/tanbir.ebooks
👦 www.facebook.com/tanbir.cox 👆 🎯www.tanbircox.blogspot.com
✐ ১৮) ক ান ির ক্ষরখ্ার ম্বত্রিখ্ণ্ডক্ষ র উপত্ররত্রস্থত কেক্ষ ান ত্রব্ু উক্ত ির ক্ষরখ্ার প্রাণ-ত্রব্ুিয় হক্ষত
িমদূরবতুী।
✐ ২০) চতু ভু ুক্ষজর ণুিক্ষয়র িমত্রষ্ট তার পত্ররিীমার অর্ু অক্ষপো বৃহত্তর।
✐ ২১) চতু ভু ুক্ষজর বাহুগুক্ষ ার মর্যত্রব্ু পেুায়ক্রক্ষম কোগ রক্ষ এ ত্রি িামান্তত্রর উৎপন্ন হয়।
✐ ২২) রম্বক্ষির বাহুগুক্ষ ার মর্যত্রব্ু পেুায়ক্রক্ষম কোগ রক্ষ এ ত্রি আয়ত উৎপন্ন হয়।
✐ ২৩) িামান্তত্ররক্ষ র ণুিয় িমান হক্ষ তা এ ত্রি আয়ত।
ত্রিভু জ অঙ্কনেঃ
প্রক্ষতয ত্রিভু ক্ষজর ত্রতনত্রি বাহু ও ত্রতনত্রি ক াণ রক্ষয়ক্ষে । ত্রিভু জ আ ার উপাত্ত গুক্ষ া ত্রনক্ষন কদওয়া হক্ষ ােঃ
১) ত্রতনত্রি বাহু
২) দুইত্রি বাহু ও তাক্ষদর অন্তভু ুক্ত ক াণ ।
৩) দুইত্রি ক াণ ও তাক্ষদর িং গ্ বাহু
৪) দুত্রি ক াণ ও এ ত্রি ত্রবপরীত বাহু ।
৫) দুইত্রি বাহু ও তাক্ষদর এ ত্রির ত্রবপরীত ক াণ ।
৬) িমক্ষ াণী ত্রিভু ক্ষজর অত্রতভু জ ও অপর এ ত্রি বাহু ।
চতু ভু ুজ অঙ্কনেঃ
ত্রননবতুী পাাঁচত্রি উপাত্ত জানা থা ক্ষ ত্রনত্রদুষ্ট চতু ভু ুজ আাঁ া োয় ।
১) চারত্রি বাহু ও এ ত্রি ক াণ
২) চারত্রি বাহু ও এ ত্রি ণু ।
৩) ত্রতনত্রি বাহু ও দুইত্রি ণু
৪) ত্রতনত্রি বাহু ও তাক্ষদর অন্তভু ুক্ত দুইত্রি ক াণ ।
৫) দুইত্রি বাহু ও ত্রতনত্রি ক াণ ।

35. 📚  www.facebook.com/tanbir.ebooks
👦 www.facebook.com/tanbir.cox 👆 🎯www.tanbircox.blogspot.com
সরেকরখ্া : যোন োকেযসীয় সমেকে দুশি শিন্দুর সমদূরিেযী শিন্দু সমূকহর সঞ্চারপথকে সরেকরখ্া
িকে।
সরেকরখ্ার ঢাে (Slope of a line) :
যোন সরেকরখ্া x অকক্ষর যনাত্মে শদকের সাকথ যয যোণ উৎপন্ন েকর োর শেকোণশমশেে
িযানকজ্কনির (tan) মানকে সরেকরখ্াশির ঢাে িকে এিং ঢােকে m দ্বারা সূশেে েরা হয়।
শেকে AB যরখ্াশি x অকক্ষর যনাত্মে শদকের সাকথ যোণ তেশর েকর।
 000
90;1800  তেশর েকর।
 AB যরখ্ার ঢাে m = tan .
PQ যরখ্াশি x অকক্ষর যনাত্মে শদকের সাকথ  0
180 যোণ উৎপন্ন েকর।
 PQ যরখ্ার ঢাে,   0
180tanm =  tan .  যোকণর পশরমাণ 00
18090 
হকে ঢাে ঋণাত্মে হকি।
এেশি সরেকরখ্ার ঢাে শনণযয় যা দুশি শনশদযি শিন্দু শদকয় অশেক্রম েকর।
PQ সরেকরখ্াশি x অকক্ষর যনাত্মে শদকের সাকথ  যোণ উৎপন্ন েকর এিং  11 y,xA ও
 22 y,xB শিন্দুদ্বয় শদকয় অশেক্রম েকর।
 PQ যরখ্ার ঢাে BARtantanm 
21
21
12
12
xx
yy
xx
yy
AR
BR





 =ভূ জ্দ্বকয়র
অন্তর/কোশিদ্বকয়র অন্তর
  :      332211 y,xC,y,xB,y,xA শিন্দু শেনশি সমকরখ্া হওয়ার িেয :

36. 📚  www.facebook.com/tanbir.ebooks
👦 www.facebook.com/tanbir.cox 👆 🎯www.tanbircox.blogspot.com
321
31
31
21
21
x,xx;
xx
yy
xx
yy






x অক্ষ ও y অকক্ষর সমান্তরাে সরেকরখ্ার সমীেরণ :
 x অকক্ষর সমান্তরাে যযকোন সরেকরখ্া সমীেরণ by  এিং
y -অকক্ষর সমান্তরাে যযকোন সরেকরখ্া সমীেরণ ax 
মন্তিয : b যনাত্মে হকে সরেকরখ্াশি x অকক্ষর b এেে উপর এিং b ঋণাত্মে হকে সরেকরখ্াশি
x অকক্ষর b এেে নীকে অিস্থান েরকি। b=0 হকে যরখ্াশি x অকক্ষর সাকথ শমকে যাকি।
 x অকক্ষর সমীেরণ 0y 
আিার a যনােম হকে সরেকরখ্া y অকক্ষর a এেে ডাকন এিং a ঋণাত্মে হকে সরেকরখ্াশি y
অকক্ষর a এেে িাকম অিস্থান েরকি।
a = 0 হকে যরখ্াশি y অকক্ষর সাকথ শমকে যাকি।
 y অকক্ষর সমীেরণ
সরেকরখ্ার আদিয সমীেরণ :
PQ সরেকরখ্াশি y অক্ষকে c শিন্দুকে য দ েকর এিং x অকক্ষর যনাত্মে শদকের সাকথ  যোণ
উৎপন্ন েকর। যশর, A (x,y) শিন্দুশি PQ এর উপর অিশস্থে এিং y অক্ষ যথকে খ্শিে অংি OC=
C.
cmxy  যা শনকণযয় সরেকরখ্ার সমীেরণ।
0c  হকে PQ সরেকরখ্ায় মূেশিন্দুগামী হয়।
 মূেশিন্দুগামী সরেকরখ্ার সমীেরণ mxy 
 11 y,x    11 xxmyy শিন্দুগামী m ঢােশিশিি সরেকরখ্ার সমীেরণ পাই
 11 y,x  22 y,xদুইশি শনশদযি শিন্দু (শিন্দু দুইশি স্থানাংে ও ) শদকয় গমনোরী সরেকরখ্ার
সমীেরণ
21
1
21
1
yy
yy
xx
xx







37. 📚  www.facebook.com/tanbir.ebooks
👦 www.facebook.com/tanbir.cox 👆 🎯www.tanbircox.blogspot.com
(i) মূেশিন্দু (0,0) এিং  11 y,x শিন্দুর সংকযাগোরী যরখ্ার সমীেরণ :
x
x
y
y
y
y
x
x
1
1
11

(ii) সরেকরখ্াশির ঢাে =
12
12
xx
yy


🎯 অক্ষদ্বয় হকে শনশদযি তদকঘযযর অংি য দ েকর এরূপ সরেকরখ্ার সমীেরণ শনণযয়। (ক দে
আেৃ শের সমীেরণ)
PQ সরেকরখ্াশি  y,xA শিন্দুগামী এিং x অক্ষকে P এিং y-অক্ষকে Q শিন্দুকে য দ েকর।
যশর OP = a এিং OQ = b সরেকরখ্ার সমীেরণ 1
b
y
a
x
সমীেরণশি মূেশিন্দুগামী হকে পাকর না োরণ (0,0) শিন্দুদ্বারা সমীেরণশি শসদ্ধ হয় না।
🎯 মূেশিন্দু যথকে যোন সরেকরখ্ার উপর অংশেে েকের তদঘযয P এিং েেশি x অকক্ষর যনাত্মে
শদকের সাকথ যোণ উৎপন্ন েরকে: সরেকরখ্ার সমীেরণ
(েে আেৃ শে সমীেরণ)

38. 📚  www.facebook.com/tanbir.ebooks
👦 www.facebook.com/tanbir.cox 👆 🎯www.tanbircox.blogspot.com
🎯   11 y,xx অকক্ষর যনাত্মে শদকের সাকথ যোণ উৎপন্ন েকর এিং শনশদযি শিন্দুগামী







sin
yy
cos
xx 11
সরেকরখ্ার সমীেরণ ;
🎯 0cbyax  0cybxa 111 দুইশি সমীেরণ ( .এিং ) দ্বারা এেই সরেকরখ্া শনকদযি
111 cc,bb,aa েরার িেয শনণযয় :সরেকরখ্াদ্বকয়র ধ্রুিেগুকো িূনয নয় এিং
111 c
c
b
b
a
a

সাযারণ যারণা
🎯 1. A (x1,y1) ও B (x2,y2) শিন্দুগামী সরেকরখ্ার ঢাে(gradient) ,
🎯2. ax+by+c=0 সরেকরখ্ার ঢাে, m = -(a/b)
🎯3. A (x1, y1), B (x2, y2) এিং C (x3, y3) শিন্দু শেনশি সমকরখ্ হকি যশদ AB এিং AC
যরখ্াদ্বকয়র ঢাে এেই হয় ।
অথযাৎ যশদ, হয়
🎯 4. x অকক্ষর সমীেরণ, y = 0
🎯5. y অকক্ষর সমীেরণ, x = 0
🎯6. x অকক্ষর সমান্তরাে সরেকরখ্ার সমীেরণ, y = b
🎯7. y অকক্ষর সমান্তরাে সরেকরখ্ার সমীেরণ, x = a
🎯8. y অক্ষ যথকে শনশদি অংি c য দ েকর এিং x
অকক্ষর সাকথ যনাত্মে যোণ θ উৎপন্ন েকর
এরূপ সরেকরখ্ার সমীেরণ, y = mx+c এখ্াকন, m = সরেকরখ্ার ঢাে = tanθ

39. 📚  www.facebook.com/tanbir.ebooks
👦 www.facebook.com/tanbir.cox 👆 🎯www.tanbircox.blogspot.com
c = 0 হকে সরেকরখ্াশি মূেশিন্দুগামী হয় এিং সমীেরণশি দাড়ায়, y = mx
🎯9.(x1,y1) শিন্দুগামী m ঢাে শিশিি সরেকরখ্ার সমীেরণ y-y1 = m(x-x1)
🎯10.(x1, y1) ও (x2,y2) শিন্দুগামী এিং y অকক্ষর সমান্তরাে নয় এরূপ যরখ্ার সমীেরণ,
=
🎯11.মূেশিন্দু (0,0) এিং (x1,y1) শিন্দুর সংকযাগোরী সরেকরখ্ার সমীেরণ, (x/x1) = (y/y1)
🎯12.x অক্ষ যথকে শনশদযি অংি a এিং y অক্ষ যথকে
শনশদযি অংি b য দ েকর এরূপ সরেকরখ্ার সমীেরণ, x/a
+ y/b = 1
সরেকরখ্াশি x অক্ষকরখ্াকে (a,0) এিং y অক্ষকরখ্াকে
(0,b) শিন্দুকে য দ েকর
🎯13.মূেশিন্দু যথকে যয সরেকরখ্ার উপর অশিে েে x অকক্ষর যনাত্মে শদকের সাকথ Θ যোণ
উৎপন্ন েকর এিং যার উপর মূেশিন্দু যথকে অশিে েকের তদঘযয p োর সমীেরণ, x cosθ +
ysinθ = p
🎯14.দুইশি সরেকরখ্ার সমীেরণ সমাযান েরকে োকদর য দশিন্দুর স্থানাি পাওয়া যায় ।
🎯15.a1x+b1y+c1 = 0 এিং a2x+b2y+c2 = 0 সরেকরখ্াদ্বকয়র য দশিন্দুগামী সরেকরখ্ার
সমীেরণ, a1x+b1y+c1+k(a2x+b2y+c2) = 0
k-এর শিশভন্ন মাকনর জ্নয সমীেরণশি শিশভন্ন সরেকরখ্া প্রোি েকর যার প্রকেযকেই উক্ত য দ
শিন্দুগামী ।
🎯16. (x1, y1) ও (x2,y2) শিন্দুদ্বয় ax+by+c = 0 যরখ্ার এেই পাকবয অিশস্থে হকি যশদ
a1x+b1y+c এিং a2x+b2y+c রাশিদ্বয় এেই শেহ্নশিশিি হয় ।
🎯17. (x1, y1) ও (x2,y2) শিন্দুদ্বয় ax+by+c = 0 যরখ্ার শিপরীে পাকবয অিশস্থে হকি যশদ
a1x+b1y+c এিং a2x+b2y+c রাশিদ্বয় শিপরীে শেহ্ন শিশিি হয় ।
🎯18. দুইশি সরেকরখ্ার ঢাে যথাক্রকম m1 ও m2 হকে োরা পরস্পর েে হকি যশদ m1✕m2 =
-1 হয় এিং োরা পরস্পর সমান্তরাে হকি যশদ m1= m2 হয় ।
🎯19. a1x+b1y+c1 = 0 এিং a2x+b2y+c2 = 0 যরখ্াদ্বয় পরস্পর েে হকি যশদ a1a2+b1b2 = 0
হয় এিং োরা পরস্পর সমান্তরাে হকি যশদ (a1/b1) = (a2/b2) হয় ।
🎯এ ত্রি ত্রব্ু (x 1, y1) ত্রদক্ষয় অত্রতক্রম ারী করখ্ার িমী রন, y - y 1 = m(x - x 1),
কেখ্াক্ষন করখ্ার ঢা m

40. 📚  www.facebook.com/tanbir.ebooks
👦 www.facebook.com/tanbir.cox 👆 🎯www.tanbircox.blogspot.com
🎯 (x 1, y1) ও (x 2, y2) ত্রব্ুগামী কে ক ান করখ্ার িমী রন,
(🎯 (x , y) ও (x 1, y1) ত্রব্ুিক্ষয়র দূরত্ব = r এবং ত্রব্ুিক্ষয়র িংক্ষোগ করখ্াংি X অক্ষের িাক্ষথ
θ ক াণ উৎপন্ন রক্ষ করখ্াত্রির িমী রনেঃ
🎯 (x 1, y1) ও (x 2, y2) ত্রব্ুিক্ষয়র িংক্ষোগ করখ্াংক্ষির ঢা েঃ
🎯y = m 1x + c 1 ও y = m 2x + c 2 করখ্ািক্ষয়র মর্যবতুী ক াণ θ হক্ষ েঃ
# এ করখ্া দুইত্রি িমান্তরা হক্ষ , m 1 = m 2
# এরা পরস্পর ম্ব হক্ষ , m 1 X m 2 = -1
🎯ax + by + c = 0 করখ্ার িমান্তরা এরূপ কেক্ষ ান করখ্ার িমী রন ax + by + k = 0,
কেখ্াক্ষন k এ ত্রি ইোমূ ধ্রব ।
🎯 ax + by + c = 0 করখ্ার ওপর ম্ব এরূপ কেক্ষ ান করখ্ার িমী রন bx - ay + k = 0,
কেখ্াক্ষন k এ ত্রি ইোমূ দ্রুব ।
🎯 a 1x + b1y + c1 = 0 এবং a2x + b2y + c 2 = 0 করখ্ািক্ষয়র কেদত্রব্ু গামী কে ক ান
ির ক্ষরখ্ার িমী রন a1x + b1y + c1 + k (a 2x + b 2y + c 2) = 0 , েখ্ন k এ ত্রি অিূনয
ধ্রব ।
🎯a 1x + b1y + c1 = 0 , a2x + b2y + c 2 = 0 এবং a 3x + b3y + c3 = 0 করখ্া িয় িমত্রব্ু
হক্ষ
🎯ax + by + c 1 = 0 , ax + by + c 2 = 0 িমান্তরা করখ্ািক্ষয়র মর্যবতুী দূরত্বেঃ
🎯 (x 1 , y 1) ত্রব্ু থক্ষ ax + by + c = 0 করখ্ার উপর অত্রঙ্কত ম্ব দূরত্বেঃ
🎯a 1x + b1y + c1 = 0 এবং a2x + b2y + c 2 = 0 করখ্ািক্ষয়র অন্তভূ ুক্ত িমত্রিখ্ন্ডক্ষ র
িমী রনেঃ
( )yx ¢¢, we›`y †_‡K 0=++ cbyax †iLvi j¤^ `~iZ¡, 22
ba
cybxa
+
+¢+¢
±
Ges `~i‡Z¡i gvb
22
ba
cybxa
+
+¢+¢
=

41. 📚  www.facebook.com/tanbir.ebooks
👦 www.facebook.com/tanbir.cox 👆 🎯www.tanbircox.blogspot.com
🎯১. যয িৃকত্তর যেন্দ্র মূেশিন্দু (0,0) এিং িযাসাযয r োর সমীেরণ। x
2
+y
2
= ry
2
🎯২. যয িৃকত্তর যেন্দ্র (h,k) এিং িযাসাযয r োর সমীেরণ। (x-h)
2
+(y-k)
2
= r
2
h=0 হকে যেন্দ্র y অকক্ষর উপর অিশস্থে। িৃকত্তর সমীেরণ, x2
+(y-k)2
=k2
k=0 হকে যেন্দ্র x অকক্ষর উপর অিশস্থে। িৃকত্তর সমীেরণ, (x-h)
2
+y
2
=h
2
🎯 ৩. িৃকত্তর সাযারণ সমীেরণ, x2
+y2
+2gx+2fy+c=0
 যযখ্াকন, িৃকত্তর যেন্দ্র ≡ (-g,-f)
এিং িযাসাযয = √(g2
+f2
-c)
g = 0 হকে যেন্দ্র y অকক্ষর উপর অিশস্থে
f = 0 হকে যেন্দ্র x অকক্ষর উপর অিশস্থে
c = 0 হকে িৃত্তশি মূেশিন্দুগামী
🎯৪. যোন িৃত্ত x অক্ষকে য দ েরকে x অক্ষ যথকে েশেযে অংি = 2√(g2
-c)
িৃৃ্ত্তশি x অক্ষকে স্পিয েরকে g2
=c
যোন িৃত্ত y অক্ষকে য দ েরকে y অক্ষ যথকে েশেযে অংি = 2√(f2
-c)
িৃত্তশি y অক্ষকে স্পিয েরকে f2
=c
🎯 ৫.যোন িৃত্ত x অক্ষকে স্পিয েরকে োর িযাসাযয হকি যেকন্দ্রর যোশির মান এিং
সমীেরণ হকি, (x-h)2
+(y-k)2
= k2
🎯৬. যোন িৃত্ত y অক্ষকে স্পিয েরকে োর িযাসাযয হকি যেকন্দ্রর ভু কজ্র মান এিং
সমীেরণ হকি, (x-h)2
+(y-k)2
= h2
🎯৭, (x1,y1) ও (x2,y2) শিন্দু দুইশির সংকযাগ সরেকরখ্াকে িযাস যকর অশিে

42. 📚  www.facebook.com/tanbir.ebooks
👦 www.facebook.com/tanbir.cox 👆 🎯www.tanbircox.blogspot.com
িৃকত্তর সমীেরণ, (x-x1)(x-x2)+(y-y1)(y-y2) = 0
🎯৮. x
2
+y
2
+2gx+2fy+c=0 িৃকত্তর এেকেশন্দ্রে অনয যোন িৃকত্তর সমীেরণ হকি,
x
2
+y
2
+2gx+2fy+c1=0
🎯 ৯. x
2
+y
2
+2gx+2fy+c=0 িৃত্ত এিং ax+by+c1 সরেকরখ্ার য দশিন্দুগামী িৃকত্তর
সমীেরণ, x
2
+y
2
+2gx+2fy+c+k(ax+by+c1)=0
🎯১০. দুইশি িৃত্ত পরস্পরকে িশহঃস্থভাকি স্পিয েরকে, োকদর িযাসাযযদ্বকয়র যযাগফে =
যেন্দ্রদ্বকয়র মযযিেযী দূরত্ব।
একক্ষকে সাযারণ স্পিযে শেনশি।
🎯১১. দুইশি িৃত্ত পরস্পরকে অন্তঃস্থভাকি স্পিয েরকে,
োকদর িযাসাযযদ্বকয়র অন্তরফে = যেন্দ্রদ্বকয়র মযযিেযী দূরত্ব
একক্ষকে সাযারণ স্পিযে এেশি।
🎯১২. দুইশি িৃত্ত পরস্পরকে য দ েরকি যশদ যেন্দ্রদ্বকয়র মযযিেযী দূরত্ব িযাসাযযদ্বকয়র
যযাগফকের যথকে য াি হয়।
একক্ষকে সাযারণ স্পিযে দুইশি।

43. 📚  www.facebook.com/tanbir.ebooks
👦 www.facebook.com/tanbir.cox 👆 🎯www.tanbircox.blogspot.com
🎯১৩. দুইশি িৃত্ত পরস্পরকে য দ িা স্পিয যোনশিই েরকি না যশদ যেন্দ্রদ্বকয়র মযযিেযী
দূরত্ব িযাসাযযদ্বকয়র যযাগফকের যেকয় িড় হয়।
একক্ষকে সাযারণ স্পিযে োরশি।
🎯 ১৪. x2
+y2
+2gx+2fy+c=0 এিং x2
+y2
+2g1x+2f1y+c1=0 িৃকত্তর য দশিন্দুগামী িৃকত্তর
সমীেরণ, x
2
+y
2
+2gx+2fy+c+k(x
2
+y
2
+2g1x+2f1y+c1)=0
🎯১৫. িশহঃস্থ যোন শিন্দু যথকে যোন িৃকত্তর ওপর দুইশি স্পিযে অিন েরা যায়।
🎯১৬. y=mx+c সরেকরখ্াশি x2
+y2
= r2
িৃত্তকে স্পিয েরকি যশদ, c = ±r√(1+m
2
)
হয়
🎯১৭. x
2
+y
2
=r
2
িৃকত্তর উপশরশস্থে (x1,y1) শিন্দুকে অশিে স্পিযকের সমীেরণ,
xx1+yy1=r
2
🎯১৮. x2
+y2
+2gx+2fy+c = 0 িৃকত্তর (x1,y1) শিন্দুকে অশিে স্পিযকের সমীেরণ,
xx1+yy1+g(x+x1)+f(y+y2)+c = 0
🎯 ১৯. িশহঃস্থ যোন শিন্দু (x1,y1) যথকে x
2
+y
2
= r
2
িৃকত্তর উপর অশিে
স্পিযেদ্বকয়র সমীেরণ, (x
2
+y
2
-r
2
)(x1
2
+y1
2
-r
2
)=(xx1+yy1-r
2
)
2
🎯২০. িশহঃস্থ শিন্দু (x1,y1) যথকে x2+y2+2gx+2fy+c=0 িৃকত্তর উপর অশিে
স্পিযেদ্বকয়র সমীেরণ,
(x
2
+y
2
+2gx+2fy+c)(x1
2
+y1
2
+2gx1+2fy1+c) =
{xx1+yy1+g(x+x1)+f(y+y1)+c}
🎯 ২১. িশহঃস্থ শিন্দু (x1, y1) যথকে x
2
+y
2
=a
2
িৃকত্তর উপর অশিে স্পিযকের তদঘযয, =
√(x
2
+y
2
-r
2
)
উক্ত শিন্দু যথকে x
2
+y
2
+2gx+2fy+c=0 িৃকত্তর উপর অশিে স্পিযকের তদঘযয, =
√(x1
2
+y1
2
+2gx1+2fy1+c)
🎯 ২২. x
2
+y
2
= r
2
িৃকত্তর (x1,y1) শিন্দুকে অশভেকের সমীেরণ, x1y-y1x=0
িৃকত্তর অশভেে এর যেন্দ্রগামী।
🎯 ২৩. x
2
+y
2
+2gx+2fy+c=0 িৃকত্তর (x1,y1) শিন্দুকে অশভেকের সমীেরণ,
(x1+g)y-(y1+f)x+fx1-gy1=0
🎯২৪. x
2
+y
2
+2g1x+2f1y+c1 = 0 এিং x
2
+y
2
+2g2x+2f2y+c2 = 0 িৃত্তদ্বকয়র সাযারণ জ্নয
এর সমীেরণ, (x
2
+y
2
+2g1x+2f1y+c1) – (x
2
+y
2
+2g2x+2f2y+c2)=0

44. 📚  www.facebook.com/tanbir.ebooks
👦 www.facebook.com/tanbir.cox 👆 🎯www.tanbircox.blogspot.com
েশনে : োকেযসীয় সমেকে এেশি শনশদযি শিন্দু ও এেশি শনশদযি সরেকরখ্া যথকে যয সি শিন্দুর
দূরকত্বর অনুপাে এেশি ধ্রুিে, োকদর যসই এেশি সঞ্চারপথ এিং োকে েশনে িো হয় ।
শনশদযি শিন্দুশিকে েশনকের উপকেন্দ্র িা যফাোস (focus) িকে।
শনশদযি সরেকরখ্াশিকে েশনকের শদোক্ষ িা শনয়ামে (directrix) িকে ।
ধ্রুি অনুপােশিকে উৎকেশন্দ্রেো (eccentricity) িো হয় এিং দ্বারা e সূশেে েরা হয় ।
e এর শিশভন্ন মাকনর জ্নয সঞ্চারপকথর আেৃ শে শভন্ন
হয় ।
e = 0 হকে সঞ্চারপথ হয় িৃত্ত (circle)
0 < e < 1 হকে সঞ্চারপথ হয় উপিৃত্ত (ellipse)
e = 1 হকে সঞ্চারপথ হয় পরািৃত্ত (parabola)
e > 1 হকে সঞ্চারপথ হয় অশযিৃত্ত (hyperbola)
পরািৃত্ত (Parabola) সম্পশেযে শে ু সংজ্ঞা:
অক্ষকরখ্া (Axis of symmetry): উপকেকন্দ্রর মযয
শদকয় শদোকক্ষর উপর অশিে েে যরখ্াশিকে পরািৃকত্তর
অক্ষকরখ্া িো হয়।
িীষযশিন্দু (Vertex): পরািৃত্ত ও অক্ষকরখ্ার য দ
শিন্দুকে পরািৃকত্তর িীষযশিন্দু িো হয়।
উপকেশন্দ্রে দূরত্ব (Focal distance): উপকেন্দ্র
যথকে পরািৃকত্তর যযকোকনা শিন্দুর দূরত্বকে উপকেশন্দ্রে
দূরত্ব িা যফাোস দূরত্ব িো হয়।
উপকেশন্দ্রে জ্যা (Focal chord): পরািৃকত্তর যয জ্যা উপকেন্দ্র শদকয় গমন েকর োকে উপকেশন্দ্রে
জ্যা িকে।
উপকেশন্দ্রে েে (Latus rectum): উপকেশন্দ্রে জ্যা অকক্ষর উপর েে হকে োকে উপকেশন্দ্রে
েে িা নাশভেে িকে। KwbK
cive„‡Ëi †¶‡Î t
cive„‡Ëi cÖwgZ mgxKiY axy 42
= ayx 42
=
i kxl©we›`yi ¯’vbvsK )0,0( )0,0(
ii Dc‡K‡›`ªi ¯’vbvsK )0,(a ),0( a
iii w`Kv‡¶i mgxKiY 0=+ ax 0=+ ay
iv A¶‡iLvi mgxKiY 0=y 0=x
v Dc‡Kw›`ªK j‡¤^i ‰`N©¨ a4 a4
vi Dc‡Kw›`ªK j‡¤^i mgxKiY 0=- ax 0=- ay

45. 📚  www.facebook.com/tanbir.ebooks
👦 www.facebook.com/tanbir.cox 👆 🎯www.tanbircox.blogspot.com
Dce„‡Ëi †¶‡Î
Dce„‡Ëi cÖwgZ mgxKiY, 12
2
2
2
=+
b
y
a
x
hLb ba > ba <
i ‡K‡›`ªi ¯’vbvsK )0,0( )0,0(
ii Dr†Kw›`ªKZv, e
2
22
2
a
ba
e
-
= 2
22
2
b
ab
e
-
=
iii e„nr A‡¶i mgxKiY 0=y 0=x
iv ¶y`ª A‡¶i mgxKiY 0=x 0=y
v e„nr A‡¶i ‰`N¨© a2 b2
vi ¶z`ª A‡¶i ‰`N¨© b2 a2
vii Dc‡K‡›`ªi ¯’vbvsK )0,( ae± ),0( be±
vii
i
w`Kv‡¶i mgxKiY
e
a
x ±=
e
b
y ±=
ix Dc‡Kw›`ªK j¤^
a
b2
2
b
a2
2
x Dc‡Kw›`ªK j‡¤^i
mgxKiY
aex ±= bey ±=
Awae„‡Ëi †¶‡Î t
cÖwgZ mgxKiY
12
2
2
2
=-
b
y
a
x
12
2
2
2
=-
a
x
b
y
i ‡K‡›`ªi ¯’vbvsK )0,0( )0,0(
ii Dr†Kw›`ªKZv, e
2
22
2
a
ba
e
+
= 2
22
2
b
ab
e
+
=
iii Avo A‡¶i mgxKiY 0=y 0=x
iv AbyeÜx A‡¶i
mgxKiY
0=x 0=y
v Avo A‡¶i ‰`N¨© a2 b2
vi AbyeÜx A‡¶i ‰`N¨© b2 a2
vii Dc‡K‡›`ªi ¯’vbvsK )0,( ae± ),0( be±
kx‡l©i ¯’vbvsK )0,( a± ),0( b±
viii w`Kv‡¶i mgxKiY
e
a
x ±=
e
b
y ±=
ix Dc‡Kw›`ªK j¤^
a
b2
2
b
a2
2
x Dc‡Kw›`ªK j‡¤^i
mgxKiY
aex ±= bey ±=

46. 📚  www.facebook.com/tanbir.ebooks
👦 www.facebook.com/tanbir.cox 👆 🎯www.tanbircox.blogspot.com
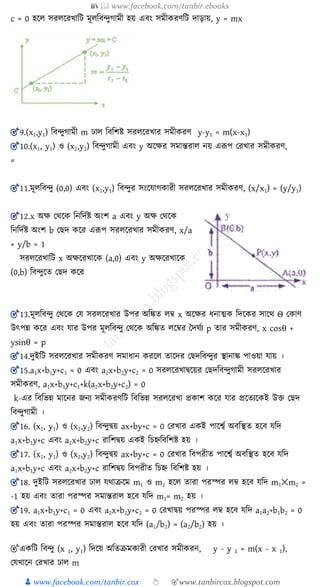
যভক্টর রাশির শনকদযিনা (Representation of vectors) :
যোন যভক্টর হকে একে শনকদযি েরার জ্নয প্রভৃ শে প্রেীে িযিহৃে হয় এিং এর
মান
যথাক্রকম ইেযাশদ দ্বারা শনকদযশিে হয় । অকনে সময় শুযু r শদকয় ও r̅ যভক্টকরর মান
প্রোি েরাহয় ।
 এেে যভক্টর (Unit vector) : যোন যভক্টর রাশিকে োর মান (Magnitude) দ্বারা ভাগ
েরকে ঐ যভক্টকরর শদকে িা োর সমান্তরাে শদকে এেে যভক্টর পাওয়া যায় ।
A̅ যোন যভক্টর ও োর শদকে িা সমান্তরাকে এেে যভক্টর â হকে,
 আয়ে এেে যভক্টর (Rectangular unit vectors) : শেমাশেে স্থানাংে িযিস্থায় যনাত্মে x,
y এিং z অকক্ষর শদকে যথাক্রকম িযিহৃে î , ĵ , k̂ এেে যভক্টরগুকোকে আয়ে এেে যভক্টর
িকে ।
অিস্থান যভক্টর (Position vector) : প্রসঙ্গ োিাকমার মূে শিন্দুর সাকপকক্ষ যোন শিন্দুর অিস্থান
যয যভক্টকরর সাহাকযয শনণযয় েরা হয় োকে অিস্থান যভক্টর িকে ।
O শিন্দুর সাকপকক্ষ P শিন্দুর অিস্থান শনকদযি েকরক অিস্থান যভক্টর । েক্ষণীয়,
;
;
েশি (Resultant) : দুই িা েকোশযে যভক্টকরর সমশিকে এেশি যভক্টর রূকপ প্রোি েরা যায়
যাকে ঐ যভক্টরগুকোর েশি িকে ।
A̅ = Axî+ Ayĵ + Azk̂; ও B̅ = Bxî + Byĵ + Bzk̂ যভক্টরদ্বকয়র েশি
A̅ + B̅ = (Ax+Bx) î+ (Ay+By) ĵ+ (Az+Bz) k̂
⇒ C̅ = Cx î+ Cyĵ+ Czk̂ [ C̅ = েশি যভক্টর]

47. 📚  www.facebook.com/tanbir.ebooks
👦 www.facebook.com/tanbir.cox 👆 🎯www.tanbircox.blogspot.com
েশির সামান্তশরে সূে (Law of parallelogram) : যোন শনশদযি শিন্দুর উপর পরস্পর θযোকণ
শক্রয়ািীে দুশি যভক্টর P̅ ও Q̅ হকে, োকদর েশি
R̅ = P̅+Q̅
R̅,P̅ এর সাকথ ϕ যোণ উৎপন্ন েরকে,
যভক্টকরর যেোর িা উি গুণন (Scalar or dot product) : A̅ও B̅ দুশি যভক্টর ও োকদর
মযযিেযী যোণ Θ হকে, োকদর যেোর গুণন,
. B̅ = ABcosθ [A̅. B̅ = B̅. A̅]
আিার, A̅= Axî+ Ay ĵ+ Azk̂; B̅ = Bxî + Byĵ + Bzk̂ হকে, ও A̅. = AxBx + AyBy + AzBz
A̅ও B̅ পরস্পর েে হকে θ = 90°
∴ A̅ . B̅ = AB cos 90° = 0 [cos90° = 0]
অথযাৎ, দুশি যভক্টর পরস্পর েে হকে োকদর যেোর গুণফে িূনয হকি ।
যভক্টর গুণন িা ক্রস গুণন (Vector or cross product) : A̅ ও B̅ দুশি যভক্টর এিং োকদর
মযযিেযী যোণ θ হকে, যভক্টর গুণন
C̅ = A̅✕B̅ = η̂ABsinθ [A̅ ✕ B̅ ≠ B̅ ✕ A̅ ]
η̂ এেশি এেে যভক্টর যা C̅ এর শদে শনকদযি েকর । আিার, A̅= Axî+ Ay ĵ+ Azk̂ ; ও B̅ =
Bxî + Byĵ + Bzk̂ হকে, A̅ও B̅ সমান্তরাে হকে, θ = 0°
∴ A̅ ✕ B̅= AB sin0° = 0 [sin0° = 0]
অথযাৎ, দুশি যভক্টর সমান্তরাে হকে োকদর যভক্টর গুণফে িূনয হকি ।
মযযিেযী যোণ শনণযয় : A̅ও B̅ দুশি যভক্টর এিং োকদর মযযিেযী যোণ θ হকে,
যভক্টকরর েে অশভকক্ষপ িা অশভকক্ষপ (Orthogonal projection) : এিং
পরস্পর θ যোকণ শক্রয়ারে দুশি যভক্টর হকে,
⇒ A̅ এর উপর B̅ এর অশভকক্ষপ =
⇒ B̅ এর উপর A̅ এর অশভকক্ষপ =

48. 📚  www.facebook.com/tanbir.ebooks
👦 www.facebook.com/tanbir.cox 👆 🎯www.tanbircox.blogspot.com

49. 📚  www.facebook.com/tanbir.ebooks
👦 www.facebook.com/tanbir.cox 👆 🎯www.tanbircox.blogspot.com

50. 📚  www.facebook.com/tanbir.ebooks
👦 www.facebook.com/tanbir.cox 👆 🎯www.tanbircox.blogspot.com
🎯 w·KvYwgwZK AbycvZ :
GKwU mij‡iLvi N~Y©‡bi d‡j †Kv‡Yi DrcwË nq| wbw`©ó cwigv‡ci †KvY Drcbœ K‡i GKwU mij‡iLv †h Ae¯’v‡b
_v‡K Zvi Dci †h †Kvb we›`y †_‡K Avw` Ae¯’v‡bi Dci j¤^ A¼b Ki‡j GKwU mg‡KvYx wÎfyR Drcbœ nq| H
wÎfy‡Ri wZwbwU evûi cwigvc‡K ci¯úi fvM Ki‡j QqwU AbycvZ cvIqv hvq| GivB w·KvYwgwZK AbycvZ|
g‡bKwi OX GKwU NyY©vqgvb mij‡iLvi Avw` Ae¯’vb| Dnv NyY©‡bi ci OY Ae¯’v‡b Ae¯’vb Kij| OY,P Gi
Dci †h †Kvb GKwU we›`y| P †_‡K OX Gi Dci PQ j¤^ Uvwb|
awi θXOY
🎯 🎯
r
y
OP
PQ
sin θ
🎯
r
x
OP
OQ
cos θ
🎯
x
y
OQ
PQ
tan θ awi, wP‡Î, OQ= x = f~wg
🎯
y
x
PQ
OQ
cot θ PQ = y = j¤^
OP = r= AwZfyR
🎯
x
r
OQ
OP
sec θ
🎯
y
r
PQ
OP
eccos θ
🎯
θ
1
θ
eccos
sin  🎯
θ
1
θ
sin
eccos 
🎯
θ
1
θ
sec
cos  🎯
θ
1
θ
cos
sec 
🎯
θ
1
θ
cot
tan  🎯
θ
1
θ
tan
cot 
🎯 1θθ 22
 cossin 🎯 1θθ 22
 tansec
🎯 1θθ 22
 coteccos 🎯 1θθ cot.tan
x
ecx
1
cossin 11 --
= ;
x
xec
1
sincos 11 --
=
x
x
1
seccos 11 --
= ;
x
x
1
cossec 11 --
=
x
x
1
cottan 11 --
= ;
x
x
1
tancot 11 --
=

51. 📚  www.facebook.com/tanbir.ebooks
👦 www.facebook.com/tanbir.cox 👆 🎯www.tanbircox.blogspot.com
🎯 †PŠ‡KvY (Quadrant) :
g‡bKwi, XXO  Ges YYO  †iLvØq O we›`y‡Z †Q` K‡i †h PviwU mg‡KvY Drcbœ K‡i Zv‡`i cÖ‡Z¨KwU‡Z
GKwU †PŠ‡KvY ev PZz©fvM (Quadrant) ejv nq| g‡bKwi, †Kvb iwkœ Zvi Avw` Ae¯’vb †_‡K ïi“ K‡i Nwoi
KvUvi NyY©‡bi wecixZ w`‡K Nyi‡Z _vK‡j cÖ_g mg‡KvY‡K cÖ_g †PŠ‡KvY (1st Quadrant) A_©vr XOY †K
cÖ_g †PŠ‡KvY e‡j| Gfv‡e NyY©‡bi d‡j Drcbœ wØZxq mg‡KvY‡K wØZxq †PŠ‡KvY
(2nd Quadrant) A_©vr OYX  †K wØZxq †PŠ‡KvY e‡j|
Abyiƒcfv‡e, YOX  = Z…Zxq ‡PŠ‡KvY (3rd
Quadrant) Ges
YXO  = PZz_© †PŠ‡KvY (4th
Quadrant) e‡j|
🎯 abvZ¥K †KvY I FYvZ¥K †KvY
‡Kvb iwk¥ hw` Zvi Ae¯’vb †_‡K Nwoi KuvUvi wecixZ w`‡K N~Y©‡bi d‡j †h †KvY Drcbœ K‡i †m †KvY‡K abvZ¥K
†KvY e‡j|
‡Kvb iwk¥ hw` Zvi Ae¯’vb †_‡K Nwoi KuvUvi w`‡K N~Y©‡bi d‡j †KvY Drcbœ K‡i †m †KvY‡K FYvZ¥K †KvY
e‡j|
🎯 †PŠ‡KvY Abyhvqx w·KvYwgwZK Abycv‡Zi wPý
🎯cÖ_g †PŠ‡KvY (1st Quadrant)-G mKj w·KvYwgwZK AbycvZ abvZ¥K|
🎯wØZxq †PŠ‡KvY (2nd Quadrant)-G eccossin, -abvZ¥K Ges Aewkó mKj w·KvYwgwZK AbycvZ
FYvZ¥K|
🎯Z…Zxq †PŠ‡KvY (3rd Quadrant)-G cottan, -abvZ¥K Ges Aewkó mKj w·KvYwgwZK AbycvZ
FYvZ¥K|
🎯PZz_© †PŠ‡KvY (4rd Quadrant)-G seccos, -abvZ¥K Ges Aewkó mKj w·KvYwgwZK AbycvZ
FYvZ¥K|
🎯 g‡b ivLvi †KŠkj all-sin-tan-cos
🎯  θ ‡Kv‡Yi w·KvYwgwZK AbycvZ :
🎯   θθ sinsin  🎯   θθ coscos 
🎯   θθ tantan  🎯   θθ cotcot 
🎯   θθ secsec  🎯   θθ eccoseccos 
🎯 





 θ
2
π
,n ‡Kv‡Yi w·KvYwgwZK AbycvZ.....
 n- †Rvo msL¨v n‡j---
mKj w·KvYwgwZK AbycvZ AcwiewZ©Z _vK‡e| ïay †PŠ‡KvY Abyhvqx wPý iƒcvš—wiZ n‡e|
 n- we‡Rvo msL¨v n‡j----
w·KvYwgwZK AbycvZ¸‡jv wb‡æv³fv‡e cwiewZ©Z n‡e-
 cossin 
 cottan 
 cotsec 
 eccossec 
🎯  θπ n †Kv‡Yi w·KvYwgwZK AbycvZ---
 mKj w·KvYwgwZK AbycvZ AcwiewZ©Z _vK‡e|
 n GKwU we‡Rvo msL¨v n‡j θ †KvYwU 3q PZz©fv‡M _vK‡e|
 n GKwU †Rvo msL¨v n‡j θ †KvYwU 1g PZz©fv‡M _vK‡e|
🎯  θπ n †Kv‡Yi w·KvYwgwZK AbycvZ-
 mKj w·KvYwgwZK AbycvZ AcwiewZ©Z _vK‡e|

52. 📚  www.facebook.com/tanbir.ebooks
👦 www.facebook.com/tanbir.cox 👆 🎯www.tanbircox.blogspot.com
 n GKwU we‡Rvo msL¨v n‡j θ †KvYwU 2q PZz©fv‡M _vK‡e|
 n GKwU †Rvo msL¨v n‡j θ ‡KvYwU 4_© PZz©fv‡M _vK‡e|
🎯  θπ2 n †Kv‡Yi w·KvYwgwZK AbycvZ-
 n †h‡Kvb ¯^vfvweK c~Y© msL¨v n‡j mKj w·KvYwgwZK AcwiewZ©Z _vK‡e|
🎯  θπ2 n †Kv‡Yi w·KvYwgwZK AbycvZ-
 n ‡h‡Kvb ¯^vfvweK c~Y© msL¨v n‡j mKj w·KvYwgwZK AcwiewZ©Z _vK‡e Ges θ †KvYwU 4_© PZz©fv‡M
_vK‡e|
কেৌত্রগ ক াক্ষণর ত্রিক্ষ াণত্রমত্রত অনুপাত:
   BsinAcosBcosAsinBAsin 
   BsinAcosBcosAsinBAsin 
   BsinAsinBcosAcosBAcos 
   BsinAsinBcosAcosBAcos 
     BsinAsinBAsinBAsin 22
 AcosBcos 22

     BsinAcosBAcosBAcos 22
 AsinBcos 22

  
BtanAtan
BtanAtan
BAtan



1
  
BtanAtan
BtanAtan
BAtan



1
  
AcotBcot
BcotAcot
BAcot



1
  
AcotBcot
BcotAcot
BAcot



1
ত্রিক্ষ াণত্রমত্রত অনুপাক্ষতর গুণফ কোগ বা ত্রবক্ষয়াগফক্ষ রূপান্তর:
      C.S,BcosAsinBAsinBAsin 2
      .S.C,BsinAcosBAsinBAsin 2
      C.C,BcosAcosBAcosBAcos 2
      S.S,BsinAsinBAcosBAcos 2
ত্রিককোণত্রিত্রিক অনুপোকির য োগ বো ত্রবক োগফল গুণফকল রূপোন্তর:

 C.S,
DC
cos
DC
sinDsinCsin
22
2



 S.Cm
DC
sin
DC
cosDsinCsin
22
2



 C.C,
DC
cos
DC
cosDcosCcos
22
2



 S.S,
CD
sin
DC
sinDcosCcos
22
2



53. 📚  www.facebook.com/tanbir.ebooks
👦 www.facebook.com/tanbir.cox 👆 🎯www.tanbircox.blogspot.com
গুত্রণত ক াক্ষণর ত্রিক্ষ াণত্রমত্রত অনুপাত: উপগুত্রণত ক াক্ষণর ত্রিক্ষ াণত্রমত্রত অনুপাত:
গুত্রণত ক াক্ষণর িূি কথক্ষ উপগুত্রণত ক াক্ষণর িূি
কবর রক্ষতেঃ - ত্রিগুত্রণত িূক্ষি 𝐴 =
𝐴
2
এবং
ত্রিগুত্রণত িূক্ষি 𝐴 =
𝐴
3
বিাক্ষ ই উপগুত্রণত
ক াক্ষণর ত্রিক্ষ াণত্রমত্রত অনুপাক্ষতর িূি পাওয়া োয়।
🎯 AcosAsinAsin 22 
Atan
Atan
2
1
2


22
2
A
cos
A
sinAsin 
2
1
2
2
2 A
tan
A
tan


🎯 AsinAcosAcos 22
2 
Atan
Atan
Asin
Acos
2
2
2
2
1
1
21
12





22
22 A
sin
A
cosAcos 
1
2
2 2

A
cos
2
21 2 A
sin
2
1
2
1
2
2
A
tan
A
tan



🎯
Atan
Atan
Atan 2
1
2
2


2
1
2
2
2 A
tan
A
tan
Atan


🎯 AcosAcos 212 2
 A
A
cos1
2
cos2 2

🎯 AcosAsin 212 2
 Acos
A
sin 1
2
2 2
🎯
Acos
Acos
Atan
21
212



Acos
AcosA
tan



1
1
2
2
🎯 AcosAcosAcos 343 3

3
3
3
4 3 A
cos
A
cosAcos 
🎯 AcosAcosAcos 334 3
 Acos
A
cos
A
cos 
3
3
3
4 3
🎯  AcosAcosAcos 33
4
13
 







 Acoscos
A
cos
3
3
4
1
3
3
🎯 AsinAsinAsin 3
433  AsinAsinAsin 3
433 
🎯 AsinAsinAsin 334 3
 Asinsin
A
sin 


3
3
3
4 3
🎯  AsinAsinAsin 33
4
13
 







 Asinsin
A
sin
3
3
4
1
3
3
🎯
Atan
AtanAtan
Atan 2
3
1
3
3



3
31
33
3
2
3
A
tan
A
tan
A
tan
Atan




54. 📚  www.facebook.com/tanbir.ebooks
👦 www.facebook.com/tanbir.cox 👆 🎯www.
t
anbircox.blogspot.com
ত্রবপরীত বৃত্তীয় ফাংিন
ত্রিক্ষ াণত্রমত্রত অনুপাত
0cos =q n‡j, ( )
2
12
p
q += n ;
1sin =q n‡j, ( )
2
14
p
q += n ;
1sin -=q n‡j, ( )
2
14
p
q -= n ;
1cos =q n‡j, pq n2=
1cos -=q n‡j, ( )pq 12 += n ;
aq sinsin == k n‡j, ( ) apq
n
n 1-+=
aq coscos == k n‡j, apq ±= n2
aq tantan == k n‡j, apq += n
0sin =q n‡j, pq n= ;
0tan =q n‡j, pq n= ;
x
ecx
1
cossin 11 --
= ;
x
xec
1
sincos 11 --
=
x
x
1
seccos 11 --
= ;
x
x
1
cossec 11 --
=
x
x
1
cottan 11 --
= ;
x
x
1
tancot 11 --
=
211
1cossin xx -= --
; 211
1sincos xx -= --
1tansec 211
-= --
xx ; 211
1sectan xx += --
1cotcos 211
-= --
xxec ; 211
1coscot xecx += --
xy
yx
yx
m1
tantantan 111 ±
=± ---
xyzxyz
xyzzyx
zyx
---
-++
=++ ----
1
tantantantan 1111
2
2
1
2
1
2
11
1
1
cos
1
2
sin
1
2
tantan2
x
x
x
x
x
x
x
+
-
=
+
=
-
= ----
{ }22111
11sinsinsin xyyxyx -±-=± ---
{ }22111
11coscoscos yxxyyx --=± ---
m
R
C
c
B
b
A
a
2
sinsinsin
===
bc
acb
A
2
cos
222
-+
=
ca
bac
B
2
cos
222
-+
=
ab
cba
C
2
cos
222
-+
=
BcCba coscos += CaAcb coscos += ; AbBac coscos +=
wÎfy‡Ri †¶Îdj, ( )( )( )csbsassCabBcaAbc ---
=
===D sin
2
1
sin
2
1
sin
2
1

55. 📚  www.facebook.com/tanbir.ebooks
👦 www.facebook.com/tanbir.cox 👆 🎯www.tanbircox.blogspot.com
  1 cx
dx
d
  cxdx
1,
1
1









nxc
n
x
dx
d n
n
1,
1
1




 nc
n
x
dxx
n
n
mxc
m
mx
dx
d
cos
sin






   c
m
mx
mxdx
sin
cos
  xcx
dx
d
cossin    cxxdx sincos
mxc
m
mx
dx
d
sin
cos






 c
m
mx
mxdx 
cos
sin
  xcx
dx
d
sincos    cxxdx cossin
mxc
m
mx
dx
d 2
sec
tan






   c
m
mx
mxdx
tan
sec2
  xcx
dx
d 2
sectan  cxdxx  tansec2
mxecc
m
mx
dx
d 2
cos
cot






 c
m
mx
mxdxec 
cot
cos 2
  xeccx
dx
d 2
coscot  cxdxxec  cotcos 2
mxmxc
m
mx
dx
d
tansec
sec






 c
m
mx
dxmxmx 
sec
tansec
  xxcx
dx
d
tansecsec  cxdxxx  sectansec
mxecmxc
m
ecmx
dx
d
cotcos
cos






 c
m
ecmx
dxmxecmx 
cos
cotcos
  xecxcecx
dx
d
cotcoscos  cecxdxxecx  coscotcos
mx
mx
ec
m
e
dx
d






 c
m
e
dxe
mx
mx

  xx
ece
dx
d
 cedxe xx

 
x
cx
dx
d 1
ln  cxdx
x
 ln
1
mx
mx
a
am
a
dx
d






ln
c
am
a
dxa
mx
mx
 ln
x
x
a
a
a
dx
d






ln
c
a
a
dxa
x
x
 ln
  xx
dx
d
tansecln  cxdxx  seclntan

56. 📚  www.facebook.com/tanbir.ebooks
👦 www.facebook.com/tanbir.cox 👆 🎯www.tanbircox.blogspot.com
  xx
dx
d
cotsinln  cxdxx  sinlncot
  xxx
dx
d
sectansecln    cxxxdx  tanseclnsec
  ecxxecx
dx
d
coscotcosln    cxecxdxecx  cotcoslncos
    
 xf
xf
xf
dx
d 
ln
 
 
  cxfdx
xf
xf


 ln
1.      
h
cfhcf
cf
h



lim0
/
2. uv এর অন্তরক সহগঃ  
dx
du
v
dx
dv
uuv
dx
d

2.  
dx
dv
wu
dx
du
vw
dx
dw
uvuvw
dx
d


57. 📚  www.facebook.com/tanbir.ebooks
👦 www.facebook.com/tanbir.cox 👆 🎯www.tanbircox.blogspot.com
3. 2
v
dx
dv
u
dx
du
v
v
u
dx
d







5.   xx
ee
dx
d

6.   aaa
dx
d xx
ln
7.  
x
x
dx
d 1
ln 
8.   e
x
x
dx
d
aa log
1
log 
9.   xx
dx
d
cossin 
10.   xx
dx
d
sincos 
11.   xx
dx
d 2
sectan 
12.   xxx
dx
d
tan.secsec 
13.   xecx
dx
d 2
coscot 
14.   xecxecx
dx
d
cot.coscos 
15.   2
1
1
1
sin
x
x
dx
d


16.   2
1
1
1
cos
x
x
dx
d




58. 📚  www.facebook.com/tanbir.ebooks
👦 www.facebook.com/tanbir.cox 👆 🎯www.tanbircox.blogspot.com
17.   2
1
1
1
tan
x
x
dx
d


18.   2
1
1
1
cot
x
x
dx
d



19.  
1
1
sec
2
1


xx
x
dx
d
20.  
1
1
cos
2
1



xx
xec
dx
d
21. uvwy  হলে, 




dx
dw
wdx
dv
vdx
du
u
uvw
dx
dy 111
22.
w
uv
y  হলে, 




dx
dw
wdx
dv
vdx
du
uw
uv
dx
dy 111
23. 2
uy  হলে,    uv
dx
d
uu
dx
dy
ln22

1. c
n
x
dxx
n
n




 1
1
2.   cx
x
dx
2
3.   cx
x
dx
ln
4.   cedxe xx
5. c
a
a
dxa
x
x
 ln
6.   cxxdx cossin
7.   cxxdx sincos
8.   cxxdx tansec2
9.   cxxdxec cotcos 2
( )
( )
( )ò =
¢
xfdx
xf
xf
ln [A_vr †hvR¨ ivwkwUi je, n‡ii Aš—iK
n‡j, Zvi †hvMR n‡ii j‡bi cig gvb n‡e|]
( )ò ò ò ò ÷
ø
ö
ç
è
æ
-= dxdxv
dx
du
vdxudxuv [A_vr `yBwU dvsk‡bi
¸Yd‡ji †hvMR = 1g dvskb´2q dvsk‡bi †hvMR-(1g
dvsk‡bi Aš—iK mnM ´ 2q dvsk‡bi †hvMR)Gi †hvMR]
[we.`ª.- †h mKj dvsk‡bi †hvMR wbY©q Kiv hvq bv ‡m mKj
dvskb‡K cÖ_g dvskb ai‡Z n‡e|]

59. 📚  www.facebook.com/tanbir.ebooks
👦 www.facebook.com/tanbir.cox 👆 🎯www.tanbircox.blogspot.com
10.  


cx
x
dx 1
2
sin
1
11.  


cx
x
dx 1
2
tan
1
12.  


cx
xx
dx 1
2
sec
1
13.   cxxdx coshsinh
14.   cxxdx sinhcosh
15.   cxxdxh tanhsec 2
16.  


cx
x
dx 1
2
sinh
1

60. 📚  www.facebook.com/tanbir.ebooks
👦 www.facebook.com/tanbir.cox 👆 🎯www.tanbircox.blogspot.com
1. c
a
x
aax
dx










1
22
tan
1
2. c
ax
ax
aax
dx




 ln
2
1
22
3. c
xa
xa
axa
dx




 ln
2
1
22
12. c
a
x
axx
dx










1
22
sec
4.   caxxc
a
x
ax
dx










221
22
lnsinh
5.   caxxc
a
x
ax
dx










221
22
lncosh
6. c
a
x
xa
dx










1
22
sin
7. c
a
xaaxx
dxax 







 

1
222
22
sinh
22
  caxx
aaxx


 22
222
ln
22
8. c
a
xaaxx
dxax 







 

1
222
22
cosh
22
  caxx
aaxx


 22
222
ln
22
9. c
a
xaxax
dxxa 







 

1
222
22
sin
22
10.     





 dxvdx
dx
du
vdxuuvdx
11.
  c
a
b
bx
ba
e
c
ba
bxbbxae
bxdxe
axax
ax











 

1
2222
tansin
cossin
sin

61. 📚  www.facebook.com/tanbir.ebooks
👦 www.facebook.com/tanbir.cox 👆 🎯www.tanbircox.blogspot.com
শিকিষ আোকরর ইনশিগ্রাে :
শনয়ম ১ : যশদ যোন ইনশিগ্রাে
   dcxbax
dx
এই আোকরর থাকে, অথযাৎ ইনশিগ্রাে হকর
এর শভেকর এে ঘাে রাশিমাো এিং এর িাশহকরও এে ঘাে রাশিমাো থাকে, েকি
এর শভেকরর রাশিমাো
2
zdcx  যশরয়া সমীেরণ েরার পর ইনশিগ্রাে েশরকে
হয়।
শনয়ম ২: যশদ যোন ইনশিগ্রাে
   cbxaxqpx
dx
2
এই আোকরর থাকে, অথযাৎ
ইনশিগ্রাে হকর এর শভেকর শদ্বঘাে রাশিমাো এিং এর িাশহকর এে ঘাে রাশিমাো
থাকে, েকি এেঘাে রাশিমাো
z
qpx
1
 যশরয়া সমীেরণ েরার পর ইনশিগ্রাে েশরকে
হয়।
শনয়ম ৩: যশদ যোন ইনশিগ্রাে
   qpxcbxax
dx
2
এই আোকরর থাকে, অথযাৎ ইনশিগ্রাে
হকর এর শভেকর এেঘাে রাশিমাো এিং এর িাশহকর শদ্বঘাে রাশিমাো থাকে, েকি
এেঘাে রাশিমাো
2
zqpx  যশরয়া সমীেরণ েরার পর ইনশিগ্রাে েশরকে হয়।
শনয়ম ৪: যশদ যোন ইনশিগ্রাে  

dx
dcx
bax
এই আোকরর থাকে, অথযাৎ ইনশিগ্রাকের েকি
এর শভেকর এেঘাে রাশিমাো এিং হকরও এর শভেকর এেঘাে রাশিমাো থাকে, েকি
েিকে
মুক্ত েশরয়া সমীেরণ েরার পর ইনশিগ্রাে েশরকে হয়।
শনয়ম ৫: যশদ যোন ইনশিগ্রাে
   dcxbax
dx
22
এই আোকরর থাকে, অথযাৎ ইনশিগ্রাে
হকর এর শভেকর শদ্বঘাে রাশিমাো এিং এর িাশহকরও শদ্বঘাে রাশিমাো থাকে, েকি
প্রথকম
z
x
1
 যশরয়া সমীেরণ েরার পর এর শভেকরর রাশিমাো
2
u যশরকে হয়
এিং পুনরায় সমীেরণ েরার পর ইনশিগ্রাে েশরকে হয়।

62. 📚  www.facebook.com/tanbir.ebooks
👦 www.facebook.com/tanbir.cox 👆 🎯www.tanbircox.blogspot.com

63. 📚  www.facebook.com/tanbir.ebooks
👦 www.facebook.com/tanbir.cox 👆 🎯www.tanbircox.blogspot.com

64. 📚  www.facebook.com/tanbir.ebooks
👦 www.facebook.com/tanbir.cox 👆 🎯www.tanbircox.blogspot.com

65. 📚  www.facebook.com/tanbir.ebooks
👦 www.facebook.com/tanbir.cox 👆 🎯www.tanbircox.blogspot.com

66. 📚  www.facebook.com/tanbir.ebooks
👦 www.facebook.com/tanbir.cox 👆 🎯www.tanbircox.blogspot.com

67. 📚  www.facebook.com/tanbir.ebooks
👦 www.facebook.com/tanbir.cox 👆 🎯www.tanbircox.blogspot.com

68. 📚  www.facebook.com/tanbir.ebooks
👦 www.facebook.com/tanbir.cox 👆 🎯www.tanbircox.blogspot.com

69. 📚  www.facebook.com/tanbir.ebooks
👦 www.facebook.com/tanbir.cox 👆 🎯www.tanbircox.blogspot.com
🎯 g¨vwUª· : GK ev GKvwaK msL¨v‡K mivmwi ev ¯—¤¢vKv‡i mvRv‡j †h AvqZvKvi web¨vm
cvIqv hvq, Zv‡K g¨vwUª· e‡j|
g¨vwUª·‡K mvaviYZ 





..
..
ev, 





..
..
ev,
..
..
Øviv cÖKvk Kiv nq|
‡hgb, 






2221
1211
aa
aa
A ev, 






2221
1211
aa
aa
A ev,
2221
1211
aa
aa
A  GwU GKwU 22 gvÎvi g¨vwUª·|
🎯 g¨vwUª‡·i gvÎv (Order) :
‡Kvb g¨vwUª‡·i mvwii msL¨v m Ges Kjvg msL¨v n n‡j g¨vwUª‡· AvKvi n‡e nm |
Bnv‡K m evB n g¨vwUª· cov nq|
‡hgb,















mnmm
n
n
a...aa
............
a...aa
a...aa
A
21
22221
11211
g¨vwUª‡·i Dcv`vb¸‡jv‡K †jLvi mgq `yBwU Subscript e¨envi Kiv nq| cÖ_g Subscript
Øviv mvwi Ges wØZxq Subscript Øviv Kjvg ev ¯—¤¢ wb‡`©k K‡i|
‡hgb ija Øviv  j,i Ae¯’v‡bi Dcv`vb eySvq hv i -Zg mvwi I j Zg Kjv‡gi msL¨v¯’‡j
Aew¯’Z|
🎯 AvqZvKvi g¨vwUª· (Rectangular matrix) :
‡h g¨vwUª‡·i mvwi I Kjv‡gi msL¨v Amgvb Zv‡K AvqZvKvi g¨wUª· e‡j|
‡hgb- 






232221
131211
aaa
aaa
A GwU GKwU 32 gvÎvi AvqZvKvi g¨vwUª·|
mvwi g¨vwUª· (Row matrix) : †h g¨vwUª‡·i GKwU gvÎ mvwi Av‡Q Zv‡K mvwi g¨vwUª· e‡j|
†hgb-  131211 aaaA  GwU GKwU 31 gvÎvi mvwi g¨vwUª·|
🎯 Kjvg g¨vwUª· (Column matrix) :
‡h g¨vwUª‡·i GKwU gvÎ Kjvg Av‡Q Zv‡K Kjvg g¨vwUª· e‡j|
‡hgb-











31
21
11
a
a
a
A GwU GKwU 13 gvÎvi Kjvg g¨vwUª·|
🎯 eM© g¨vwUª· (Square matrix) :
‡h g¨vwUª‡·i mvwi I Kjv‡gi msL¨v mgvb Zv‡K eM© g¨vwUª· e‡j| †hgb- 






2221
1211
aa
aa
A , GwU
GKwU 22 gvÎvi eM© g¨vwUª·|
🎯 we‡`nx g¨vwUª· (Null matrix) :
‡h g¨vwUª‡·i mvwi I Kjv‡gi cÖ‡Z¨KwU Dc`vb k~b¨ Zv‡K we‡`nx g¨vwUª· e‡j| †hgb







00
00
A
🎯 GKK g¨vwUª· (Unit/Identity matrix) :

70. 📚  www.facebook.com/tanbir.ebooks
👦 www.facebook.com/tanbir.cox 👆 🎯www.tanbircox.blogspot.com
‡h eM© g¨vwUª‡·i cÖavb KY© eivei Aew¯’Z Dcv`vb¸‡jv GK Ges evwK Dcv`vb¸‡jv k~b¨,
Zv‡K GKK g¨vwUª· ev A‡f`K g¨vwUª· e‡j|
‡hgb- 






10
01
A , GwU GKwU GKK g¨vwUª·| hvi gvÎv 22
🎯 KY© g¨vwUª· (Diagonal matrix) :
‡h eM© g¨vwUª‡·i cÖavb KY© eivei Aew¯’Z Dcv`vb¸‡jv e¨ZxZ evwK Dcv`vb¸‡jv k~b¨ Zv‡K
KY© g¨vwUª· e‡j| †hgb-







22
1
0
0
a
a
A GwU GKwU KY© g¨vwUª·| hvi gvÎv 22
🎯 †¯‹jvi g¨vwUª· (Scalar matrix) :
‡h KY© g¨vwUª‡·i Ak~b¨ Dcv`vb¸‡jv GKB ev mgvb Zv‡K KY© g¨vwUª· e‡j| †hgb- 






a
a
A
0
0
, GwU GKwU †¯‹jvi g¨vwUª·| hvi gvÎv 22 .
🎯 wÎfyRvKvi g¨vwUª· (Triangular matrix) :
‡h eM© g¨wUª‡·i cÖavb K‡Y©i wb毒 me¸‡jv Dcv`vb k~b¨, Zv‡K DaŸ© wÎfyRvKvi g¨vwUª&· e‡j|
†hgb-











33
2322
131211
00
0
a
aa
aaa
A GwU GKwU DaŸ© wÎfyRvKvi g¨vwUª·| hvi gvÎv& 33
‡h eM© g¨vwUª‡·i cÖavb K‡Y©i DaŸ©¯’ me¸‡jv Dcv`vb k~b¨ Zv‡K wbæ wÎfyRvKvi g¨vwUª· e‡j|
‡hgb-











333231
2221
11
0
00
aaa
aa
a
A GwU GKwU wbæwÎfyRvKvi g¨vwUª·| hvi gvÎv 33
🎯 cÖwZmg g¨vwUª· (Symmetric matrix) :
GKwU eM© g¨vwUª·  ijaA  cÖwZmg n‡e jiij aa  nq|
A g¨vwUª· e‡j| †hgb-











cfg
fbh
gha
A GwU GKwU cÖwZmg g¨vwUª·| hvi gvÎv 33 .
🎯 AcÖwZmg g¨vwUª· (Skewsymmetricmatrix) :
GKwU eM© g¨vwUª·  ijaA  AcÖwZmg n‡e jiij aa  nq|
‡hgb-












cfg
fbh
gha
A GwU GKwU AcÖwZmg g¨vwUª·| hvi gvÎv 33 .
🎯 wms¸jvi g¨vwUª· (Singular matrix) :
‡h KY© g¨vwUª‡·i wbY©q‡Ki gvb k~b¨, Zv‡K wms¸jvi g¨vwUª· e‡j| †hgb- 






42
105
A GwU
GKwU wms¸jvi g¨vwUª·| hvi gvÎv 22 KviY 02020
42
105
A
🎯 we¤^ g¨vwUª· (Transpose matrix) :

71. 📚  www.facebook.com/tanbir.ebooks
👦 www.facebook.com/tanbir.cox 👆 🎯www.tanbircox.blogspot.com
‡Kvb g¨vwUª·  ijaA  Gi me¸‡jv mvwi‡K Kjv‡g A_ev, me¸‡jv Kjvg‡K mvwi‡Z cwiYZ
Ki‡j †h g¨vwUª· cvIqv hvq Zv‡K A g¨vwUª‡·i we¤^ g¨vwUª· e‡j| Bnv‡K T
A Øviv cÖKvk
Kiv nq| †hgb-











321
321
321
ccc
bbb
aaa
A Ges
A g¨vwUª‡·i we¤^ g¨vwUª·,











333
222
111
cba
cba
cba
A
🎯 g¨vwUª‡·i †hvM I we‡qvM (Addition and subtraction of matrix) :
 ijaA  Ges  ijbB  `yBwU 22 g¨vwUª·|
 ijcC  Ggb GKwU g¨vwUª· hvi cÖwZwU Dcv`vb A I B Gi mswk­ ó Dcv`vb؇qi †hvMdj|
G‡¶‡Î C †K AI B g¨vwUª· `yBwUi †hvMdj e‡j| Avevi, hw` C Gi cÖwZwU Dcv`vb A I
B Gi mswk­ ó Dcv`vb؇qi we‡qvMdj nq, Z‡e C †K A I B g¨vwUª· `yBwUi we‡qvMdj
e‡j|
‡hgb- 












2221
1211
2221
1211
bb
bb
B,
aa
aa
A
myZivs AI B g¨vwUª· `yBwUi †hvMdj,









22222121
12121111
baba
baba
BAC
Ges AI B g¨vwUª· `yBwUi we‡qvMdj,









22222121
12121111
baba
baba
BAC
🎯 g¨vwUª‡·i ¸Y (Multiplication of matrices) :
AI B `yBwU g¨vwUª· n‡j Zv‡`i ¸Ydj‡K AB Øviv msÁvwqZ Kiv n‡e| A I B ¸Y‡bi Rb¨
Dc‡hvMx n‡e hw` A(A_©vr evgcv‡k¦©i g¨vwUª‡·i) Gi Kjvg msL¨v B (A_©vr Wvbcv‡k¦©i
g¨vwUª‡·i) Gi mvwii msL¨v ci¯úi mgvb nq| Ab¨_vq Giv ¸Yb‡hvM¨ n‡e bv| Avevi AB
msÁvwqZ n‡j BA msÁvwqZ bvI n‡Z cv‡i Ges BA msÁvwqZ n‡j AB msÁvwqZ bvI n‡Z
cv‡i|
hw` A GKwU rm gvÎvi g¨vwUª· nq Ges B GKwU nr  gvÎvi g¨vwUª· nq Z‡e AB GKwU
nm gvÎvi g¨vwUª· n‡e| hvi cÖ‡Z¨KwU Dcv`vb wb‡æv³ Dcv‡q wbY©q Kiv n‡e|
A g¨vwUª‡·i i-Zg mvwii cÖ‡Z¨KwU Dcv`vb‡K B g¨vwUª‡·i j-Zg Kjv‡gi Abym½x Dcv`vb¸‡jv
Øviv ¸Y K‡i G‡`i mK‡ji †hvM wb‡j AB g¨vwUª‡·i i-Zg mvwiI j-Zg Kjv‡gi †Q`we›`yi
Dcv`vb cvIqv hv‡e|
‡hgb- 












2221
1211
2221
1211
bb
bb
B,
aa
aa
A
myZivs AI B g¨vwUª‡·i `yBwUi ¸Ydj,













2221
1211
2221
1211
bb
bb
aa
aa
ABC









2222122121221121
2212121121121111
babababa
babababa

72. 📚  www.facebook.com/tanbir.ebooks
👦 www.facebook.com/tanbir.cox 👆 🎯www.tanbircox.blogspot.com
ত্রনণুায়ক্ষ র র্মু (Properties of Determinants) :
১. ত্রনণুায়ক্ষ র ক ান িাত্রর বা ক ান াক্ষমর উপাদানগুক্ষ া িূণয হক্ষ ত্রনণুায়ক্ষ র মান িূণয হয় ।
২. ত্রনণুায়ক্ষ র িাত্রর ও ামিমূহ পরস্পর স্থান ত্রবত্রনময় রক্ষ অথুাৎ িাত্ররগুক্ষ া াক্ষম এবং ামগুক্ষ া
িাত্ররক্ষত পত্ররণত রক্ষ ত্রনণুায়ক্ষ র মান অপত্ররবত্রতুত থাক্ষ ।
৩. ত্রনণুায়ক্ষ র পািাপাত্রি দুত্রি াম ত্র ংবা দুত্রি িাত্রর পরস্পর স্থান ত্রবত্রনময় রক্ষ ত্রনণুায়ক্ষ র ত্রচে
পত্ররবত্রতুত হয় ত্র ন্তু িাংখ্যমান অপত্ররবত্রতুত থাক্ষ ।
৪. ত্রনণুায়ক্ষ র দুত্রি াম ত্র ংবা দুত্রি িাত্রর অত্রভন্ন (Identical) হক্ষ ত্রনণুায়ক্ষ র মান িূণয হয় ।
৫. ত্রনণুায়ক্ষ র ক ান িাত্রর বা াক্ষমর উপাদানগুক্ষ াক্ষ েথাক্রক্ষম অপর িাত্রর বা াক্ষমর অনুরূপ
উপাদাক্ষনর িহগুণ িারা গুণ রা হক্ষ । গুণফ গুক্ষ ার িমত্রষ্ট িূণয হয় ।
৬. ত্রনণুায়ক্ষ র ক ান িাত্রর বা াক্ষমর প্রক্ষতয ত্রি উপাদানক্ষ ক ান ত্রস্থর িংখ্যা িারা গুণ রক্ষ , ত্রনণুায়ক্ষ র
মানক্ষ ও কিই ত্রস্থর িংখ্যা িারা গুণ রা হয় ।
৭. ত্রনণুায়ক্ষ র ক ান িাত্রর বা াক্ষমর প্রত্রতত্রি উপাদানক্ষ ক ান ত্রস্থর িংখ্যা িারা গুণ রক্ষ েত্রদ েথাক্রক্ষম
অনয ক ান িাত্রর বা াম পাওয়া োয় তক্ষব ত্রনণুায়ক্ষ র মান িূণয হয় ।
৮. ত্রনণুায়ক্ষ র ক ান িাত্রর বা াক্ষমর প্রত্রতত্রি উপাদান দুইত্রি পদ ত্রনক্ষয় গত্রঠত হক্ষ ত্রনণুায় ত্রিক্ষ অনয দুত্রি
ত্রনণুায়ক্ষ র িমত্রষ্টরূক্ষপ প্র াি রা োয় ।
৯. ত্রনণুায়ক্ষ র ক ান িাত্রর বা াক্ষমর প্রত্রতত্রি উপাদান েথাক্রক্ষম অনয এ ত্রি িাত্রর বা াক্ষমর অনুরূপ
উপাদাক্ষনর এ ত্রি গুত্রণত িারা বৃত্রদ্ধ ব হ্রাি রা হক্ষ ত্রনণুায়ক্ষ র মান অপত্ররবত্রতুত থাক্ষ ।
ত্রনণুায়ক্ষ র িাহাক্ষেয ির িমী রণ কজাক্ষির িমার্ান :
১. িমী রণ কজাক্ষির চ িমূক্ষহর িহগগুক্ষ া পািাপাত্রি াম ত্রহক্ষিক্ষব ত্রনক্ষয় ত্রনণুায়ক্ষ র মান ত্রনণুয় রক্ষত
হক্ষব । উক্ত ত্রনণুায় ক্ষ D বা Δ িারা িূত্রচত রা হয় ।
২. এরপর উক্ত ত্রনণুায়ক্ষ র প্রথম ামক্ষ িমী রণক্ষজাক্ষির ধ্রুব পদ িারা প্রত্রতস্থাত্রপত কর ত্রনণুায়ক্ষ র
মান ত্রনক্ষ প্রথম াক্ষমর িংত্রেষ্ট চ ক্ষ র জনয এ ত্রি ত্রনণুায়ক্ষ র মান পাওয়া োক্ষব ।
৩. এভাক্ষব প্রত্রত াক্ষমর জনয প্রত্রক্রয়া (ii) পুনরাবৃত্রত্ত ক্ষর েথাক্রক্ষম Dx/Δx, Dy/Δy, Dz/Δz ......
ইতযাত্রদ ত্রনণুায়ক্ষ র মান পাওয়া োক্ষব ।
৪. x/Δx = y/Δy = z/Δz = ...... = 1/Δ ইতযাত্রদর মান ত্রনণুয় রা োয় ।
🎯 wbY©vqK (Determinent) : wbY©vqK GKwU dvskb hvi †Wv‡gb mKj eM© g¨vwUª‡·i †mU
Ges hvi †Kv‡Wv‡gb ev¯—e ev RwUj msL¨vi †mU|






dc
ba
GKwU g¨vwUª· n‡j H g¨vwUª‡·i wbY©vqK
dc
ba
hvi gvb bcadD 
🎯 wbY©vq‡Ki we¯—vi,
333
222
111
cba
cba
cba
D 
33
22
1
33
22
1
33
22
1
ba
ba
c
ca
ca
b
cb
cb
a 
     233212332123321 babaccacabcbcba  🎯 Abyivwk : wbY©vq‡Ki †Kvb Dcv`vb †h
mvwi Ges Kjv‡gi †Q`we›`y‡Z Aew¯’Z †m mvwi Ges Kjvg ev` w`‡q Aewkó Dcv`vb¸‡jvi
Ae¯’vb cwieZ©b bv K‡i MwVZ wbY©vqK‡K H Dcv`v‡bi Abyivwk e‡j|

73. 📚  www.facebook.com/tanbir.ebooks
👦 www.facebook.com/tanbir.cox 👆 🎯www.tanbircox.blogspot.com
g‡bKwi,
333
222
111
cba
cba
cba
D 
1a Gi Abyivwk
33
22
cb
cb

1b Gi Abyivwk
33
2
ca
ca 2

1c Gi Abyivwk
33
22
ba
ba

🎯 mn¸YK : wbY©vq‡Ki Dc`v‡bi mn¸YK nj Gi wPwýZ Abyivwk A_©vr †Kvb Dcv`v‡bi
Abyivwki evgcv‡k¦© h_v‡hvM¨ wPý emv‡j Gi mn¸YK cvIqv hvq| †h Dcv`v‡bi mn¸YK
wbY©q Ki‡Z n‡e Zvi Ae¯’vb †h mvwi I Kjv‡gi †Q`we›`y, †m mvwi I Kjv‡gi †hvMdj †Rvo
n‡j abvZ¥K wPý Ges we‡Rvo n‡j FYvZ¥K wPý emv‡Z n‡e|
Z…Zxq ch©v‡qi wbY©vq‡Ki Dcv`v‡bi mn¸YK wbY©q Ki‡Z Abyivwki c~‡e© e¨eüZ h_v‡hvM¨
wPý wbæiƒc:



g‡bKwi,
333
222
111
cba
cba
cba
D 
1a Gi mn¸YK
33
22
cb
cb

1b Gi mn¸YK
33
2
ca
ca 2

1c Gi mn¸YK
33
22
ba
ba

🎯 wbY©vq‡Ki ¸Yvejx :
 ‡Kvb wbY©vq‡Ki GKwU mvwi A_ev GKwU Kjv‡gi mKj Dcv`vb k~b¨ nq Z‡e wbY©vqKwUi
gvb k~b¨ n‡e|
‡hgb- 0
0 33
22
11
333
22 
cb
cb0
cb0
cba
cba
000
D 2
 †Kvb wbY©vq‡Ki mvwi‡K Kjv‡g ev Kjvg‡K mvwi‡Z cwieZ©b Ki‡j wbY©vq‡Ki gvb
AcwiewZ©Z _v‡K|
‡hgb-
321
32
32
333
22
11
ccc
bbb
aaa
cba
cba
cba
D 1
1
2
1

 †Kvb wbY©vq‡Ki `yBwU cvkvcvwk mvwi ev Kjvg ci¯úi ¯’vb wewbgq Ki‡j wbY©vq‡Ki gvb
AcwiewZ©Z _v‡K wKš‘ wPý cwiewZ©Z nq|

74. 📚  www.facebook.com/tanbir.ebooks
👦 www.facebook.com/tanbir.cox 👆 🎯www.tanbircox.blogspot.com
‡hgb-
333
22
12
333
22
11
cab
cab
cab
cba
cba
cba
D 2
1
2
1

 †Kvb wbY©vq‡Ki `yBwU mvwi ev Kjvg GKB n‡j wbY©vq‡Ki gvb k~b¨ n‡e|
‡hgb-
333
22
11
caa
caa
caa
D 2
1
 = 0
 †Kvb wbY©vq‡Ki `yBwU mvwi ev Kjvg Gi Dcv`vb¸‡jv ci¯ú‡ii mgvbycvwZK n‡j H
wbY©vq‡Ki gvb k~b¨ n‡e|
‡hgb- 0
333
222
111
333
222
111

caa
caa
caa
k
caka
caka
caka
D
 †Kvb wbY©vq‡Ki GKwU mvwi ev Kjv‡gi Dcv`vb¸‡jvi cÖ‡Z¨KwU Dcv`vb wb‡q MwVZ n‡j
H wbY©vqK‡K `yBwU wbY©vq‡Ki mgwóiƒ‡c cÖKvk Kiv hvq|
‡hgb-
3333
2222
1111
cbak
cbak
cbak
D




333
222
111
333
222
111
cba
cba
cba
cbk
cbk
cbk

 †Kvb wbY©vq‡Ki GKwU mvwi ev Kjv‡gi Dcv`vb¸‡jv‡K GKB msL¨v Øviv ¸Y K‡i H
wbY©vq‡K GKwU mvwi ev Kjv‡gi Abyiƒc Dcv`vb¸‡jvi mv‡_ †hvM ev we‡qvM Ki‡j wbY©vq‡Ki
gvb AcwiewZ©Z _v‡K|
‡hgb-
333
222
111
cba
cba
cba
D 
3333
2222
1111
cbkba
cbkba
cbkba




🎯 wbY©vq‡Ki mvnv‡h¨ GKNvZ mgxKiY‡Rv‡Ui mgvavb----
 wØPjK wewkó GKNvZ mgxKiY‡Rv‡Ui mgvavb----
g‡bKwi, GKNvZ mgxKiY‡RvU,
222
111
cybxa
cybxa


g‡bKwi, 1221
22
11
baba
ba
ba
D 
1221
22
11
bcbc
bc
bc
Dx 
1221
22
11
caca
ca
ca
Dy 
‡µgvi c✕wZ‡Z mgvavb K‡i cvB,

75. 📚  www.facebook.com/tanbir.ebooks
👦 www.facebook.com/tanbir.cox 👆 🎯www.tanbircox.blogspot.com
DD
y
D
x
yx
1
 GLv‡b 0D
D
D
x x
 Ges
D
D
y
y

myZivs wb‡Y©q mgvavb †mU 







D
D
.
D
D yx
🎯 wÎPjK wewkó GKNvZ mgxKiY‡Rv‡Ui mgvavb-----
g‡bKwi, GKNvZ mgxKiY‡RvU
3333
2222
1111
dzcybxa
dzcybxa
dzcybxa



g‡bKwi,
333
222
111
cba
cba
cba
D 
333
222
111
cbd
cbd
cbd
Dx 
333
222
111
cda
cda
cda
Dy 
333
222
111
dba
dba
dba
Dz 
‡µgvi c✕wZ‡Z mgvavb K‡i cvB
DD
z
D
y
D
x
zyx
1
 GLv‡b 0D
D
D
y,
D
D
x
yx
 Ges
D
D
z z

myZivs wb‡Y©q mgvavb †mU 





D
D
.
D
D
.
D
D zyx

76. 📚  www.facebook.com/tanbir.ebooks
👦 www.facebook.com/tanbir.cox 👆 🎯www.tanbircox.blogspot.com
n! = n ✕(n-1)✕(n-2)✕.... ✕3✕2✕1
5! = 1.2.3.4.5 = 5.4.3.2.1 = 120
n! = n(n-1)!
0! = 1
একটি ঘটনা n উপাকয় করার পকর তিিীয় আকরকটি ঘটনা যতে m উপাকয় করা যায়, িাহক দুইটি ঘটনা একসাকে mn উপাকয় ঘটাকনা
যায়।
n সংখ্যক ভিন্ন ভিন্ন ভিভিস থেকক r সংখ্যক ভিন্ন ভিন্ন ভিভিস ভিকে যত প্রকাকে সািাকিা যাে, তাে
প্রকতেকটিকক এক একটি ভিন্যাস িকে। ইহাকক
n
P
r
দ্বাো সুভিত কো হে।
কতগুকো ভিন্ন ভিন্ন ভিভিস থেকক ককেকটি ভিকে সািাকত িেকে
n
P
r
কেখ্াক্ষন:
r প্রত্রতত্রি ত্রবনযাক্ষির আ ার অথুাৎ মূৃ্ উপাদাক্ষনর কিি কথক্ষ প্রত্রতবাক্ষর ত্রঠ তত্রি উপাদান ত্রনক্ষয় প্রত্রতত্রি
ত্রবনযাি গত্রঠত হক্ষে তার িংখ্যা
n কিই কিক্ষির আ ার ো কথক্ষ ত্রবনযাক্ষির উপাদান গৃহীত হয় বা মূ উপাদাক্ষনর কিক্ষি ত্রবদযমান কমাি
উপাদান িংখ্যা
! হ ফযাক্টত্ররয়া অপাক্ষরির।
🎯 n msL¨K wewfbœ wRwbm n‡Z cÖwZevi r msL¨K wRwbm wb‡q hZ cÖKvi web¨vm MVb Kiv hvq, (†hLv‡b n I r †hvM‡evaK
Ges rn 
r
n
P Gi gvb A_©vr n msL¨K wewfbœ wRwbm n‡Z cÖwZevi r wRwbm msL¨K wb‡q hZ cÖKvi web¨vm MVb Kiv hvq
n msL¨K wewfbœ wRwbm Øviv r msL¨K ¯’vb hZfv‡e c~iY Kiv hvq ZvB wb‡Y©q web¨vm msL¨vi mgvb|
 !rn
!n
Pr
n


🎯 me¸‡jv wRwbm wfbœ GKB bq, Giƒc n msL¨K wewfbœ wRwb‡mi web¨vm
wRwb‡mi †gvU msL¨v n | G‡`i g‡a¨ r msL¨K wRwbm GK RvZxq, s msL¨K wRwbm Ab¨ GK RvZxq, t msL¨K wRwbm
Ab¨ Avi GK RvZxq,....., evKx¸‡jv wfbœ wfbœ| G‡`i‡K hZ cÖKv‡i mvRv‡bv hvq Zvi msL¨v
myZivs wb‡Y©q web¨vm msL¨v
......t!s!r
!n

🎯 n msL¨K wRwbm †_‡K r msL¨K wRwb‡mi web¨vm | hLb GKB e¯‘ r msL¨K evi cybive„Ë _v‡K|
n msL¨K wRwbm n‡Z cÖwZev‡i r msL¨K wRwb‡mi wb‡q web¨¯’ Ki‡Z n‡e, hLb GKB e¯‘ r msL¨K evi cybive„Ë n‡Z
cv‡i|

77. 📚  www.facebook.com/tanbir.ebooks
👦 www.facebook.com/tanbir.cox 👆 🎯www.tanbircox.blogspot.com
n msL¨K wRwbm n‡Z cÖwZev‡i r msL¨K wRwbm wb‡q G‡`i‡K hZfv‡e mvRv‡bv hv‡e, n msL¨K wRwbm n‡Z r msL¨K
wRwbm wb‡q r msL¨K duvKv ¯’v‡b G‡`i‡K ZZfv‡e emv‡bv hv‡e|
r msL¨K ¯’v‡b n msL¨K wRwbm r
n fv‡e emv‡bv hvq|
myZivs wb‡Y©q web¨vm msL¨v r
n
🎯 cÖ_g n msL¨K we‡Rvo msL¨vi ¸Ydj
!n
!n
n
2
2
🎯 েেগুকো শভন্ন শভন্ন শজ্শনস যথকে সিগুকো িা শভন্ন শভন্ন অক্ষর শনকয় গশিে এেশি িকের
সিগুকো অক্ষর শনকয় সাজ্াকে িেকে
n
P
n
িা n!
🎯 n msL¨K wewfbœ wRwbm n‡Z cÖwZevi r msL¨K wRwbm wb‡q hZ cÖKvi mgv‡ek cvIqv
hvq, Zv‡`i msL¨v (†hLv‡b n I r †hvM‡evaK Ges rn  )
wb‡Y©q mgv‡ek msL¨v,
 !rn!r
!n
Cr
n


🎯 n msL¨K wewfbœ wRwb‡mi cÖwZev‡i r msL¨K wRwbm wb‡q MwVZ mgv‡ek, n msL¨K
wewfbœ wRwbm †_‡K cÖwZev‡i rn  msL¨K wRwbm wb‡q MwVZ mgv‡ek msL¨vi mgvb|
rn
n
r
n
CC 
n msL¨K wewfbœ wRwb‡mi cÖwZev‡i r msL¨K wRwbm wb‡q MwVZ mgv‡ek msL¨v r
n
C
myZivs n msL¨K wewfbœ wRwb‡mi cÖwZev‡i rn  msL¨K wRwbm wb‡q MwVZ mgv‡ek rn
n
C 
🎯 r
n
r
n
r
n
CCC 1
1

 
🎯 r
n
r
n
r
n
CCC 2
1
11 



🎯 r
n
r
n
r
n
CCC  

1
11

78. 📚  www.facebook.com/tanbir.ebooks
👦 www.facebook.com/tanbir.cox 👆 🎯www.tanbircox.blogspot.com
ক ান িনার িম্ভাবযতার গাত্রণত্রত পত্ররমাপ =
অথুাৎ িম্ভাবযতা =
ক ান িনা A িার িম্ভাবযতা P(A) হক্ষ 0≤P(A) ≤1 অথুাৎ A িার িম্ভাবযতা িূক্ষনযর কচক্ষয় ম
নয় এবং এ অক্ষপো অত্রর্ নয় ।
ত্রনত্রিত িনার িম্ভাবযতা 1
অিম্ভব িনার িম্ভাবযতা 0
ক ান িনা A িার িম্ভাবযতা P(A) এবং না িার িম্ভাবযতা P(A0) হক্ষ , P(A)+P(A0)=1 অথুাৎ
ক ান িনা িা এবং না িার িম্ভাবযতার িমত্রষ্ট 1
িম্ভাবযতার িংক্ষোগিূি :
P ( A অথবা B) অথুাৎ P(A⋃B) = P(A)+P(B)
েত্রদ A ও B দুত্রি অবজুনিী িনা হয় তক্ষব, P(A⋃B) = P(A)+P(B)-P(A⋂B)
বজুনিী িনার কেক্ষি : দুইত্রি বজুনিী িনার কেক্ষ ান এ ত্রি িার িম্ভাবযতা তাক্ষদর
পৃথ ভাক্ষব িার িম্ভাবযতার িমত্রষ্টর িমান । েত্রদ A ও B দুত্রি বজুনিী িনা হয় তক্ষব
অবজুনিী িনার কেক্ষি : দুইত্রি অবজুনিী িনার কেক্ষ ান এ ত্রি িার িম্ভাবযতা তাক্ষদর
পৃথ ভাক্ষব িার িম্ভাবযতার কোগফ কথক্ষ তাক্ষদর এ িাক্ষথ িার িম্ভাবযতার ত্রবক্ষয়াগফক্ষ র
িমান ।
িম্ভাবযতার গুণন িূি : ত্রবত্রভন্ন স্বার্ীন িনা এ ক্ষি িার িম্ভাবযতা তাক্ষদর পৃথ ভাক্ষব িার
িম্ভাবযতার গুণফক্ষ র িমান ।
েত্রদ A ও B দুত্রি স্বার্ীন িনা হয় তক্ষব, P(A⋂B) = P(A).P(B)
িতুার্ীন িম্ভাবযতা : েত্রদ A ও B পরস্পর বজুনিী দুত্রি িনা হয় এবং P(B) > 0 হয় তক্ষব B
িার িতুার্ীক্ষন A িার িম্ভাবযতা,
P(A/B) = P(A⋂B) / P(B)
অনুরূপভাক্ষব, েত্রদ হয় P(A) > 0 তক্ষব A িার িতুার্ীক্ষন B িার িম্ভাবযতা,
P(B/A) = P(A⋂B) / P(A)

79. 📚  www.facebook.com/tanbir.ebooks
👦 www.facebook.com/tanbir.cox 👆 🎯www.tanbircox.blogspot.com
বাস্তব বা ত্রচন্তা জগক্ষতর িু-িংজ্ঞাত্রয়ত বস্তুর িমাক্ষবি বা িংগ্রহক্ষ কিি বক্ষ । কেমন, বাং া, ইংক্ষরত্রজ ও
গত্রণত ত্রবষক্ষয় ত্রতনত্রি পাঠযবইক্ষয়র কিি। প্রথম দিত্রি ত্রবক্ষজাড় স্বাভাত্রব িংখ্যার কিি, পূণুিংখ্যার কিি,
বাস্তব িংখ্যার কিি ইতযাত্রদ।
কিিক্ষ িার্ারণত ইংক্ষরত্রজ বণুমা ার বড় হাক্ষতর অের A,B,C,..........X ,Y,Z িারা প্র াি রা হয়।
কেমন, 2, 4, 6 িংখ্যা ত্রতনত্রির কিি A = {2, 4, 6}
কিক্ষির প্রক্ষতয বস্তু বা িদিযক্ষ কিক্ষির উপাদান (element) ব া হয়। কেমন, B = {a, b} হক্ষ , B
কিক্ষির উপাদান a এবং b; উপাদান প্র াক্ষির ত্রচে ‘∈’.
a ∈ B এবং পড়া হয় a, B এর িদিয (a belongs to B)
b ∈ B এবং পড়া হয় b, B এর িদিয (b belongs to B)
উপক্ষরর B কিক্ষি c উপাদান কনই।
c Bএবং পড়া হয় c, B এর িদিয নয় (c does not belong to B).
কিি প্র াক্ষির পদ্ধত্রত (Method of describing Sets) :
কিিক্ষ প্রর্ানত দুই পদ্ধত্রতক্ষত প্র াি রা হয়। েথা : (১) তাত্র া পদ্ধত্রত (Roster Method বা
Tabular Method) এবং (২) কিি গঠন পদ্ধত্রত (Set Builder Method)
(১) তাত্র া পদ্ধত্রত : এ পদ্ধত্রতক্ষত কিক্ষির ি উপাদান িুত্রনত্রদুষ্টভাক্ষব উক্ষ খ্ ক্ষর ত্রিতীয় বন্ধনী { } এর
মক্ষর্য আবদ্ধ রা হয় এবং এ াত্রর্ উপাদান থা ক্ষ ’ মা’ বযবহার ক্ষর উপাদানগুক্ষ াক্ষ আ াদা রা
হয়।কেমন, A = {a, b}, B ={2, 4, 6}, C={ত্রন য়, ত্রতিা, শুভ্রা} ইতযাত্রদ।
(২) কিি গঠন পদ্ধত্রত : এ পদ্ধত্রতক্ষত কিক্ষির ি উপাদান িুত্রনত্রদুষ্টভাক্ষব উক্ষ খ্ না ক্ষর উপাদান
ত্রনর্ুারক্ষণর জনয িার্ারণ র্ক্ষমুর উক্ষল্লখ্ থাক্ষ । কেমন : A = {x : x স্বাভাত্রব ত্রবক্ষজাড় িংখ্যা}, B = {x : x
নবম কেত্রণর প্রথম পাাঁচজন ত্রিোথুী} ইতযাত্রদ।
এখ্াক্ষন, ': ' িারা ‘এরূপ কেন’ বা িংক্ষেক্ষপ ‘কেন’ (such that) কবাঝায়। কেক্ষহতু এ পদ্ধত্রতক্ষত কিক্ষির
উপাদান ত্রনর্ুারক্ষণর জনয িতু বা ত্রনয়ম (Rule) কদওয়া থাক্ষ , এ জনয এ পদ্ধত্রতক্ষ Rule Method ও ব া
হয়।
িমান কিি : কেক্ষ ান কিি A=B হক্ষব েত্রদ A কিক্ষির ি িদিয B কিক্ষির িদিয হয় এবং B কিক্ষির ি
িদিয A কিক্ষির িদিয হয় । অথুাৎ,
A=B হক্ষব েত্রদ এবং ক ব েত্রদ হক্ষ x ∈ B হয় এবং x ∈ B হক্ষ x ∈ A হয় ।
ফাাঁ া কিি/ িূণয কিি : কে কিক্ষির ক ান িদিয কনই তাক্ষ ফাাঁ া বা িূণয (Empty) কিি ব া হয় । িূণয কিিক্ষ
িংক্ষ ত িারা প্র াি রা হয় ।
উপক্ষিি : েত্রদ A কিক্ষির প্রত্রতত্রি উপাদান B কিক্ষিরও উপাদান হয় তক্ষব A ক কিক্ষির B উপক্ষিি (Subset)
ব া হয় । এবং A ⊂ B ত্র ক্ষখ্ তা প্র াি রা হয় । উপক্ষিি কবাঝাক্ষত ⊆ ত্রচেও বযবহার রা হয় । A ⊆ B হয়
েত্রদ ও ক ব েত্রদ x ∈ A হক্ষ x ∈ B হয় । ক ান কিক্ষির িদিয িংখ্যা n হক্ষ ঐ কিক্ষির জনয 2n
িংখ্য
উপক্ষিি পাওয়া োক্ষব ।

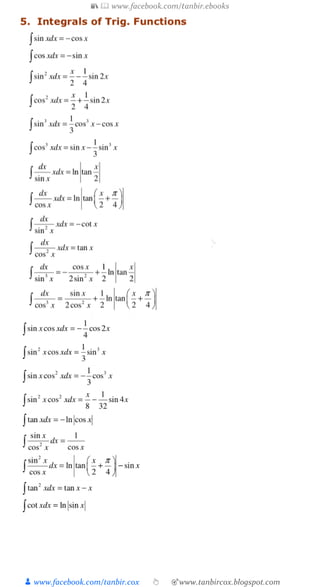
80. 📚  www.facebook.com/tanbir.ebooks
👦 www.facebook.com/tanbir.cox 👆 🎯www.tanbircox.blogspot.com
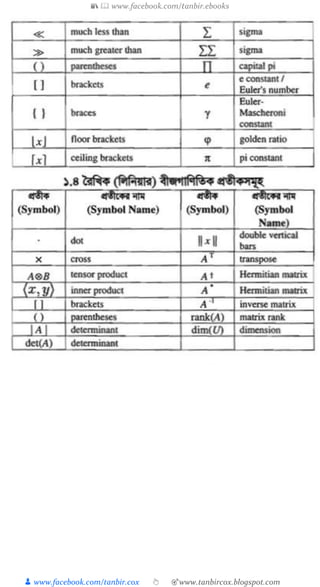
প্র ৃ ত উপক্ষিি : কিি A ক B এর প্র ৃ ত উপক্ষিি (Proper Subset) ব া হয় েত্রদ A ⊂ B এবং A ≠ B হয়
। A, B এর প্র ৃ ত উপক্ষিি কবাঝাক্ষত A ⊊ B ক খ্া হয় । ক ান কিক্ষির িদিয িংখ্যা n হক্ষ ঐ কিক্ষির জনয
(2n
-1) িংখ্য প্র ৃ ত উপক্ষিি পাওয়া োক্ষব ।
িত্রক্ত কিি : ক ান কিক্ষির উপক্ষিিিমূক্ষহর কিিক্ষ ঐ কিক্ষির িত্রক্ত কিি (Power set) বক্ষ । ক ান কিি A এর
পাওয়ার কিিক্ষ P(A) িারা প্র াি রা হয় ।
িাত্রবু কিি : আক্ষ াচনার্ীন ি কিিক্ষ তথা তাক্ষদর উপাদানিমূহক্ষ এ ত্রি ত্রবক্ষিষ কিক্ষির অন্তভূ ুক্ত
ত্রবক্ষবচনা রা হয় । কিই ত্রবক্ষিষ কিিক্ষ ঐ আক্ষ াচনার িাত্রবু কিি (Universal Set) ব া হয় এবং িার্ারণত
⋃ প্রতীক্ষ র িাহাক্ষেয প্র াি রা হয় ।
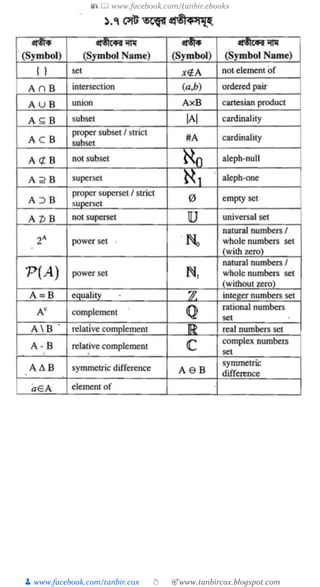
বযবত্রর্ : a ও b বাস্তব িংখ্যা এবং a<b হক্ষ এর চারত্রি ত্রবক্ষিষ র্রক্ষনর উপক্ষিিক্ষ a ও b প্রান্তত্রবত্রিষ্ট বযবত্রর্
(Interval) ব া হয় । দ্রষ্টবয, ি বাস্তব িংখ্যার কিিক্ষ R িারা িূত্রচত রা হয় ।
a কথক্ষ b পেুন্ত কখ্া া (Open) বযবত্রর্ : ]a,b[ = (a,b) = {x∣x ∈ R এবং a<x<b}
a কথক্ষ b পেুন্ত বদ্ধ (Closed) বযবত্রর্ : [a,b] = {x∣x ∈ R এবং a≤x≤b}
a কথক্ষ b পেুন্ত কখ্া া-বদ্ধ বযবত্রর্ : ]a,b] = (a,b] = {x∣x ∈ R এবং a<x≤b}
a কথক্ষ b পেুন্ত বদ্ধ-কখ্া া বযবত্রর্ : [a,b[ = [a,b) = {x∣x ∈ R এবং a≤x<b}
িংক্ষোগ কিি : দুত্রি কিি A এবং B এর ি উপাদান ত্রনক্ষয় (ক ান উপাদাক্ষনর পুনরাবৃত্রত্ত না ক্ষর) গত্রঠত
কিিক্ষ A এবং B এর িংক্ষোগ কিি ব া হয় । ো A⋃B প্রতীক্ষ র মার্যক্ষম প্র াি রা হয় । অথুাৎ,
A⋃B = {x ∣ x ∈ অথবা x ∈ b}
দ্রষ্টবয, x ∉ A⋃B হয় েত্রদ ও ক ব েত্রদ x ∉ A এবং X ∉ B হয় ।
িংজ্ঞা কথক্ষ এিা স্পষ্ট কে, i. A⋃B = B⋃A [ত্রবত্রনময় ত্রবত্রর্]
ii. A ⊆ A⋃B এবং B ⊆ A⋃B
কেদ কিি : দুত্রি কিি A এবং B এর ি িার্ারণ (Common) উপাদান ত্রনক্ষয় গত্রঠত কিিক্ষ A এবং B এর
কেদ কিি ব া হয় । ো A⋂B ত্র ক্ষখ্ প্র াি রা হয় । অথুাৎ
A⋂B = {x ∣ x ∈ A এবং x ∈ B}
দ্রষ্টবয, x ∉ A⋂B হয় েত্রদ ও ক ব েত্রদ x ∉ A অথবা x ∉ B
িংজ্ঞা কথক্ষ এিা স্পষ্ট কে, i. AB = BA [ত্রবত্রনময় ত্রবত্রর্]
ii. A⋂B ⊂ A এবং A⋂B ⊂ B
ত্রনক্ষেদ কিি : দুত্রি কিি A এবং B ত্রনক্ষেদ কিি বা িংক্ষেক্ষপ ত্রনক্ষেদ ব া হয় েত্রদ A এবং B এর মক্ষর্য ক ান
িার্ারণ উপাদান ত্রবদযমান না থাক্ষ । অথুাৎ, A⋂B = ϕ েত্রদ হয় ।
অন্তর কিি : A এবং B দুত্রি কিি হক্ষ , কে িমস্ত উপাদান A কিক্ষি আক্ষে ত্র ন্তু B কিক্ষি কনই, এরূপ উপাদান
ত্রনক্ষয় গত্রঠত কিিক্ষ A এবং B এর অন্তর কিি (Differecne Set) বক্ষ । A এবং B এর অন্তর কিিক্ষ A-B
বা AB ত্রনক্ষয় প্র াি রা হয় । এ ইভাক্ষব, B কিক্ষি আক্ষে ত্র ন্তু A কিক্ষি কনই এরূপ উপাদান ত্রনক্ষয় গত্রঠত
কিিক্ষ B এবং A এর অন্তর কিি বক্ষ । B এবং A এর অন্তর কিিক্ষ B-A বা BA ত্র ক্ষখ্ প্র াি রা হয় ।
A-B = AB = {X ∣ X ∈ A এবং X ∉ B}
B-A = BA = {X ∣ X ∈ B এবং X ∉ A}
দ্রষ্টবয : i. A-B ⊂ A
ii. B-A ⊂ B
পূর কিি : ক ান কিক্ষির উপাদানগুক্ষ াক্ষ বাদ ত্রদক্ষয় িাত্রবু কিক্ষির অনযানয িমস্ত উপাদান ত্রনক্ষয় গত্রঠত কিিক্ষ
উক্ত কিক্ষির পূর কিি বক্ষ । A ক ান কিি হক্ষ A এর পূর (Complement) কিিক্ষ A′ প্রতী িারা
প্র াি রা হয় । অথুাৎ,
A′ = U-A = {X ∣ X ∈ U এবং X ∉ A}
ক্রমক্ষজাড় : দুত্রি িংখ্যার ক্রমক্ষজাক্ষড় (Ordered Pair) এ ত্রি িংখ্যাক্ষ প্রথম এবং অপরত্রিক্ষ ত্রিতীয় উপাদান
র্রা হয় । (a,b) িারা এ ত্রি ক্রমক্ষজাড় ত্রনক্ষদুি রা হয় োর প্রথম পদ a এবং ত্রিতীয় পদ b । ক্রমক্ষজাড় (a,b)
ও (c,d) িমান হয় অথুাৎ, (a,b) = (c,d) হয় েত্রদ ও ক ব েত্রদ a=c এবং b=d হয় ।

81. 📚  www.facebook.com/tanbir.ebooks
👦 www.facebook.com/tanbir.cox 👆 🎯www.tanbircox.blogspot.com
াক্ষতুিীয় গুণজ কিি : েত্রদ A এবং B দুত্রি কিি হয়, তক্ষব A এর উপাদানগুক্ষ াক্ষ প্রথম পদ ও B এর
উপাদানগুক্ষ াক্ষ ত্রিতীয় পদ র্ক্ষর গত্রঠত ক্রমক্ষজাক্ষড়র কিিক্ষ A এবং B এর াক্ষতুিীয় গুণজ (Cartesian
Product) কিি বক্ষ । ো A×B প্রতী িারা প্র াি রা হয় । অথুাৎ,
A×B = {(x,y) ∣ x ∈ A এবং y ∈ B}
A×B = {(x,y) ∣ x ∈ B এবং y ∈ A}
এবং িার্ারণভাক্ষব, A×B ≠ B×A
দ্রষ্টবয, A কিক্ষি p িংখ্য বস্তু এবং B কিক্ষি q িংখ্য বস্তু থা ক্ষ A×B কিক্ষি pq িংখ্য বস্তু থা ক্ষব ।
কিক্ষির িংক্ষোগ ত্রবত্রর্ (Associative Law) : A,B,C কেক্ষ ান ত্রতনত্রি কিি হক্ষ ,
(A⋃B)⋃C = A⋃(B⋃C)
(A⋂B)⋂C = A⋂(B⋂C)
কিক্ষির বণ্টন ত্রবত্রর্ (Distributive Law) : A,B,C কেক্ষ ান ত্রতনত্রি কিি হক্ষ ,
A⋃(B⋂C) = (A⋃B)⋂(A⋃C)
A⋂(B⋃C) = (A⋂B)⋃(A⋂C)
অক্ষভদ ত্রবত্রর্ (Identity Law) : A কেক্ষ ান কিি এবং U িাত্রবু কিি হক্ষ ,
A⋃ϕ = A
A⋂U = A
A⋃U = U
A⋂ϕ = ϕ
পূর ত্রবত্রর্ (Complement Law) : U িাত্রবু কিি, A কেক্ষ ান এ ত্রি কিি এবং ϕ ফাাঁ া কিি এবং U′, A′
এবং ϕ′ েথাক্রক্ষম তাক্ষদর পূর কিি হক্ষ ,
A⋃A′ = U
A⋂A′ = ϕ
(A′)′ = A
U′ = ϕ
ϕ′ = U
দয মরগাক্ষনর ত্রবত্রর্ (De Morgan’s Law) : A,B কেক্ষ ান দুইত্রি কিি এবং A′ ও B′ তাক্ষদর পূর কিি হক্ষ ,
(A⋃B)′ = A′⋂B′
(A⋂B)′ = A′⋃B′
A িান্ত (finite) কিি হক্ষ , A এর উপাদান িংখ্যা আমরা n(A) ত্রদক্ষয় প্র াি ত্রর ।
A এবং B দুইত্রি িান্ত কিি ফক্ষ A⋃B ও এ ত্রি িাই কিি । কিক্ষেক্ষি,
n(A⋃B) = n(A)+n(B)-N(A⋂B)
n((A⋃B)′) = n(S)-n(A⋃B) [A এবং B উভক্ষয় S এর উপক্ষিি হক্ষ ]
= n(S)-n(A)-n(B)+n(A⋂B)
A,B,C িাই কিি ফক্ষ ,
n(A⋃B⋃C) = n(A)+n(B)+n(C)-n(A⋂B)-n(B⋂C)-n(C⋂A)+n(A⋂B⋂C)

82. 📚  www.facebook.com/tanbir.ebooks
👦 www.facebook.com/tanbir.cox 👆 🎯www.tanbircox.blogspot.com

83. 📚  www.facebook.com/tanbir.ebooks
👦 www.facebook.com/tanbir.cox 👆 🎯www.tanbircox.blogspot.com

84. 📚  www.facebook.com/tanbir.ebooks
👦 www.facebook.com/tanbir.cox 👆 🎯www.tanbircox.blogspot.com

85. 📚  www.facebook.com/tanbir.ebooks
👦 www.facebook.com/tanbir.cox 👆 🎯www.tanbircox.blogspot.com

86. 📚  www.facebook.com/tanbir.ebooks
👦 www.facebook.com/tanbir.cox 👆 🎯www.tanbircox.blogspot.com

87. 📚  www.facebook.com/tanbir.ebooks
👦 www.facebook.com/tanbir.cox 👆 🎯www.tanbircox.blogspot.com

88. 📚  www.facebook.com/tanbir.ebooks
👦 www.facebook.com/tanbir.cox 👆 🎯www.tanbircox.blogspot.com
(Viber,Whatsapp & imo Available)
tanbir.cox
www.facebook.com/tanbir.cox

89. 📚  www.facebook.com/tanbir.ebooks
👦 www.facebook.com/tanbir.cox 👆 🎯www.tanbircox.blogspot.com
অেবা, এখাকন👆তিক করুন অেবা, এখাকন👆তিক করুন অেবা, এখাকন👆তিক করুন
অনলাইনন পড়নে বা লাইভ প্রিপ্রভউ 🕮 দেখনেেঃ এখানন 👆প্রিক করুন
এখানন👆প্রিক করুন , অথবা এখানন 👆প্রিক করুন , অথবা এখানন 👆প্রিক করুন
এই প্রিপ্রভপ্রি গুনলা সম্পনকে দকান প্রকছু বুঝনে সমস্যা হনল অথবা আন া প্রবস্তাপ্র ে েথয জানা জন্য আমা সানথ ...
👨 দেসবুকঃ www.facebook.com/tanbir.cox 🖄 ই-দমই ঃ tanbir.cox@gamil.com
এ মাধ্যনম দ াগান াগ ক নে পান ন ...

90. 📚  www.facebook.com/tanbir.ebooks
👦 www.facebook.com/tanbir.cox 👆 🎯www.tanbircox.blogspot.com
📚 💻 E-Educational Disc 📀 A-Z Educational eBooks & Software (প্রক্ষয়াজনীয় ত্রিোমূ
বাং া বই ও িফিওয়ার)
🎬 E-Educational Disc 📀 Spoken English & English Grammar Tutorial with Bangla( এইচত্রড
এত্রনক্ষমিন ত্রনভুর বাং া ত্রিক্ষিাত্ররয়া )
📚 E-education Disc 📀 3D Visual eBooks with full HD Picture (স্টু ক্ষডন্টক্ষদর জনয মাত্রিত্রমত্রডয়া
ত্রনভুর এইচত্রড ত্রপ চার বই ও িফিওয়যার)
📀 বাং াক্ষদক্ষির ত্রবখ্যত ক খ্ ক্ষদর জনত্রপ্রয় বাং া গল্প ও উপনযাি িমগ্র [৩০০০+ বাং া ই-বু াক্ষ িন]
+বাং া অনুবাদ ৃ ত বই +িব িমগ্র াক্ষ িন
📀 Genuine -Windows Xp Sp3 & Windows 7, 8.1, 10 Pro & Ultimate 64 &32 bit ও
Driver Pack Solution 16 এর DVD+৩০০ ত্রি বাং া বই

91. 📚  www.facebook.com/tanbir.ebooks
👦 www.facebook.com/tanbir.cox 👆 🎯www.tanbircox.blogspot.com
📀 100% Computer Security & Speed up [আপনার ত্রম্পউিারক্ষ রাখ্ুন ১০০% ভাইরাি মুক্ত ও বৃত্রদ্ধ
রুন আপনার ত্রম্পউিাক্ষরর গত্রত ]
📀 Office & Documents Software Collection DVD [আপনার আত্রফত্রিয়া োবতীয় াক্ষজর জনয
দর াত্রর িব িফিওয়যার ]
📀 Design , Graphics & Photo Editing DVD[ [হক্ষয় োন কিরা ত্রডজাইনার ]প্রক্ষয়াজনীয় ফু ভািুন
িফিওয়যার , ত্রভত্রড়ও ত্রিউক্ষিাত্ররয়া ও বাং া ]
📀 Internet & Web programming DVD[প্রক্ষয়াজনীয় ফু ভািুন িফিওয়যার , ত্রভত্রড়ও ত্রিউক্ষিাত্ররয়া ও
বাং া বই ]
📀 Mobile Utility soft & Application DVD [কমাবাই জনয (1000+) বাং া ত্রিেণীয় অযাত্রিক্ষ িান ও
৩০০+ কমাবাই ভািুন বাং া বই ]
📀Multimedia & Windows Style[ ত্রম্পউিার এর জনয দর াত্রর িব মাত্রিত্রমত্রডয়া িফিওয়যার ও উইক্ষন্ডাজ
ক িু্র কদখ্াক্ষনার জনয িব িফিওয়যার ]
📀 A-Z Bangla & English Complete Video Tutorial (200 ত্রজত্রব িম্পূণু ত্রিক্ষিাত্ররয়া , ৫০০০ ত্রভত্রডও
যািাগত্রর আ াক্ষর িাজাক্ষনা)