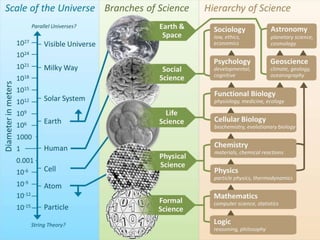
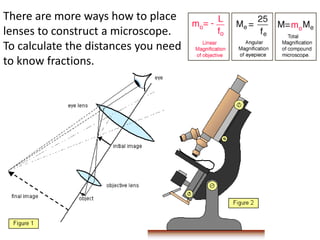
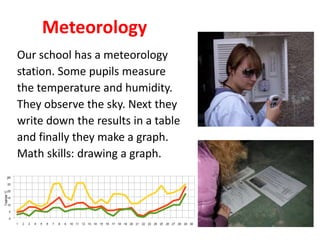
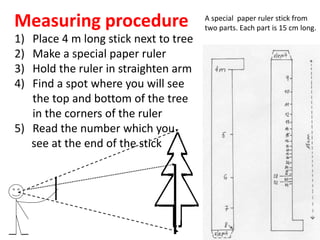
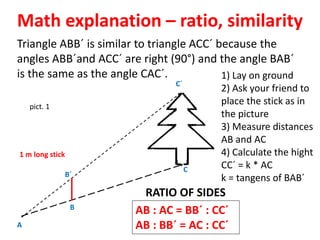
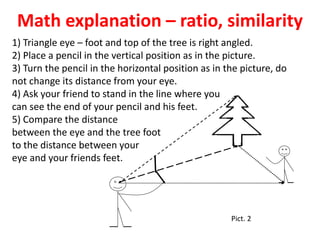
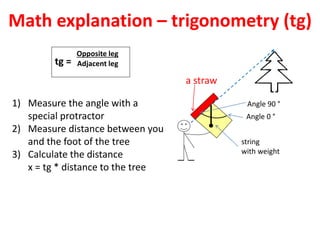
1) Mathematics is used extensively in science for measurements, calculations, and showing relationships between scientific properties. Arithmetic, algebra, and advanced mathematics like calculus are applied in areas like physics, chemistry, and astronomy. 2) Specific mathematical concepts are used for different scientific domains. For example, fractions and decimals are used in chemistry for compositions, graphs are made in meteorology, and trigonometry is applied to measure tree heights. 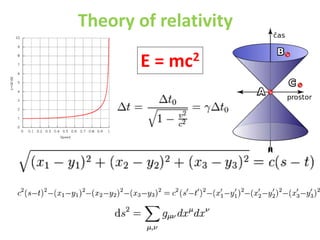3) Advanced mathematics is necessary for more complex theories and equations, like relativity or quantum mechanics. Overall, mathematics provides the means to make quantitive analyses and predictions in scientific disciplines.

1. Math in Science
1) Research – Science disciplines
- Definitions and examples
- Math in Science
2) Primary Math in Science
Teaching: An effective key to self-learning
This project is funded by European Union.

2. This teacher is thinking about Math in Science.

3. Míša, Klára, Susan, and Verča
are ready for the lesson. 

5. Maths in Physical Science
Mathematics is used in Physical Science very often,
for example arithmetic, algebra and advanced
mathematics may be used:
• to calculate the measurements of objects and
their characteristics
• to show the relationship between different
functions and properties.
• to establish values
• to solve simple equations or formulae
• to converse units
• in classical or everyday Physics, normal values are
used to solve equations.

6. Fields of Math used in Science
Mathematics is used in Physical Science for
measurements and to show relationships.
• Arithmetic consists of simple operations with
numbers and values.
• Algebra is used to show relationships before
the measured numbers are used for
calculations.
• Higher math is used for complex relationships
between properties.

7. Arithmetic conventions
In using Arithmetic, we can add, subtract,
multiply and divide numbers. We also use
fractions and decimals.
• Addition and subtraction
• Multiplication and division
• Order of mathematical operations
• Use of parentheses
• Fractions and decimals

8. Relationships in Algebra
Algebra uses letters to denote a relationship between
characteristics. Usually, they are just abbreviations for
the characteristic. For example, energy is denoted
by E and velocity by v.
Newton came up with the relationship between force,
mass and acceleration. His equation says that force
equals the mass of an object times its acceleration. To
avoid writing out this sentence, we use the
symbols F for force, m for mass and a for acceleration.
Thus, the equation can be written: F = ma.
This allows us to substitute values for two items and
get a value for the third.

9. Advanced mathematics
• Calculus, differential equations and other
advanced mathematics are used in advanced
Physical Science calculations and equations.
• One example of where and why advanced
mathematics must be used can be seen in the
simple gravity equations. F = m*g is the equation
for the force of gravity. But that equation is only an
approximation for items falling close to Earth. The
actual equation is related to the masses of the
bodies.

10. Theory of relativity
E = mc2

11. Consclusion: Importance of equations,
Algebra, Arithmetic, Calculus
You can study the facts of science with little or no
math. However, in many areas of science (Physics,
Astronomy, and Chemistry) equations are used to
make calculations. In such cases, you need some
knowledge or Algebra and Arithmetic to work with
the equations and make the calculations.
Advanced science subjects may require knowledge
of advanced math, such as Calculus. Even for
students of Psychology is important knowledge of
Math as they must take a statistics class.
Biopsychology is 100 per cent science.

12. Math topics used in Science
- Units (Physics, Chemistry)
- Stars (Physics – Astronomy)
- Temperature (Physics)
- Movement (Physics)
- Maps (Geography)
- Animals and Humans (Biology)
- Climate Change (Geography, Ecology)
- Density (Chemistry)
- Gravity (Physics, Astronomy)
- Time (Physics)
- Expansion due to Heat (Physics, Chemistry)
- Family (Social studies, Budget)

13. Chemistry – Composition of food
The majority of the food we eat is composed by nutrients:
proteins, fats, mineral salts, and vitamins. During our visit
in Desio in Italy we made an experiment to prove what is in
carrot. Math skills: writing data into a table.

14. Chemistry – Composition of food
First we cut and pressed carrot. We
measured the liquid. Next we
added some substances to prove
what nutrients a carrot consists:
water, protein, fat, sugar, and fiber.

15. Meteorology
Our school has a meteorology
station. Some pupils measure
the temperature and humidity.
They observe the sky. Next they
write down the results in a table
and finally they make a graph.
Math skills: drawing a graph.

16. Paedology and geology
We prepared a map of our school
playground. Then we picked places and
dug a hole. We collected samples from
different depths. We studied those
samples, measured pH factor and put
the results in a table. We used GPS to
put our holes in the map. Math skills:
using coordinates and tables.

18. Botany
Botany is also interested in the growth of plants.
We learnt how to measure the width and height
of trees. Of course, special electronic gadgets
were developed but we used simpler methods
which are based on knowledge of PI constant
and similarity or triangles.

19. Botany facts: Trees grow more or less evenly. Most trees increase
their circumference by 2.5 cm per year. This means that a tree with
circumference 2.5 m is about 100 years old if it has enough space.
The circumference of a tree is measured in the height of 1.30 m.
This method can not be used for trees which are very young nor
very old, so it is only approximate. This method can not be applied
to poplars as they grow far faster than other trees nor trees growing
in the high mountains.
Measuring procedure - age of a tree
1) Measure the circumference of a tree
2) You can measure the diameter and
calculate it (c = PI * diameter)
3) Find out the age of the tree (c : 2.5)

20. Measuring procedure
1) Place 4 m long stick next to tree
2) Make a special paper ruler
3) Hold the ruler in straighten arm
4) Find a spot where you will see
the top and bottom of the tree
in the corners of the ruler
5) Read the number which you
see at the end of the stick
A special paper ruler stick from
two parts. Each part is 15 cm long.

21. Math explanation – ratio, similarity
1 m long stick
pict. 1
A
B
C
C´
B´
Triangle ABB´ is similar to triangle ACC´ because the
angles ABB´and ACC´ are right (90°) and the angle BAB´
is the same as the angle CAC´.
AB : AC = BB´ : CC´
AB : BB´ = AC : CC´
RATIO OF SIDES
1) Lay on ground
2) Ask your friend to
place the stick as in
the picture
3) Measure distances
AB and AC
4) Calculate the hight
CC´ = k * AC
k = tangens of BAB´

22. Math explanation – ratio, similarity
Pict. 2
1) Triangle eye – foot and top of the tree is right angled.
2) Place a pencil in the vertical position as in the picture.
3) Turn the pencil in the horizontal position as in the picture, do
not change its distance from your eye.
4) Ask your friend to stand in the line where you
can see the end of your pencil and his feet.
5) Compare the distance
between the eye and the tree foot
to the distance between your
eye and your friends feet.

23. Opposite leg
tg = Adjacent leg
Math explanation – trigonometry (tg)
1) Measure the angle with a
special protractor
2) Measure distance between you
and the foot of the tree
3) Calculate the distance
x = tg * distance to the tree
a straw
Angle 90 °
Angle 0 °
string
with weight

24. Law of the lever: M1a = M2b
Levers are used to lift heavy weights with the least amount of
effort. In the photos the weight on the left hand side is been
lifted by the person because of the lever. The longer the 'rod'
the easier it is to lift the weight. Under normal circumstances
the person would not be able to lift the weight at all.
The fulcrum is the place where the rod pivots (or rotates).

25. In this case, the power into the lever equals the power
out, and the ratio of output to input force is given by
the ratio of the distances from the fulcrum to the points
of application of these forces.

26. A microscope – lenses, focal length
A microscope is an instrument that uses a lens or a series of
lenses to magnify small objects. When you look through a
simple microscope, you are looking through a biconvex lens
made of glass. Light from the object passes through the lens
and is bent (refracted) towards your eye, so it seems as
though it comes from a much bigger object.

27. There are more ways how to place
lenses to construct a microscope.
To calculate the distances you need
to know fractions.

28. Fractals
A fractal is a natural phenomenon or a mathematical
set that exhibits a repeating pattern that displays at every
scale. It is also known as expanding symmetry or
evolving symmetry. On the left, frost crystals occurring
naturally on cold glass form fractal patterns. On the right,
we constructed a fractal triangle.

29. Computers and robots
There is no doubt that advanced math is needed to
construct computers and robots and to write programs
which help normal people to communicate with them.

30. Sources
• https://en.wikipedia.org/wiki/Branches_of_science
• http://www.school-for-
champions.com/science/math.htm#.Vrh9aBjhDcs
• https://www.shodor.org/unchem/math/
• http://science.howstuffworks.com/math-
concepts/fractals.htm
• http://www.ncpublicschools.org/docs/accountability/c
ommon-exams/released-
forms/highschool/science/physics/formula-sheet.pdf
• https://en.wikipedia.org/wiki/Fractal#/media/File:Frost
_patterns_2.jpg
• https://en.wikipedia.org/wiki/Focal_length
• https://en.wikipedia.org/wiki/Theory_of_relativity
• Other pictures and drawings are from our teacher Mrs.
Buroňová