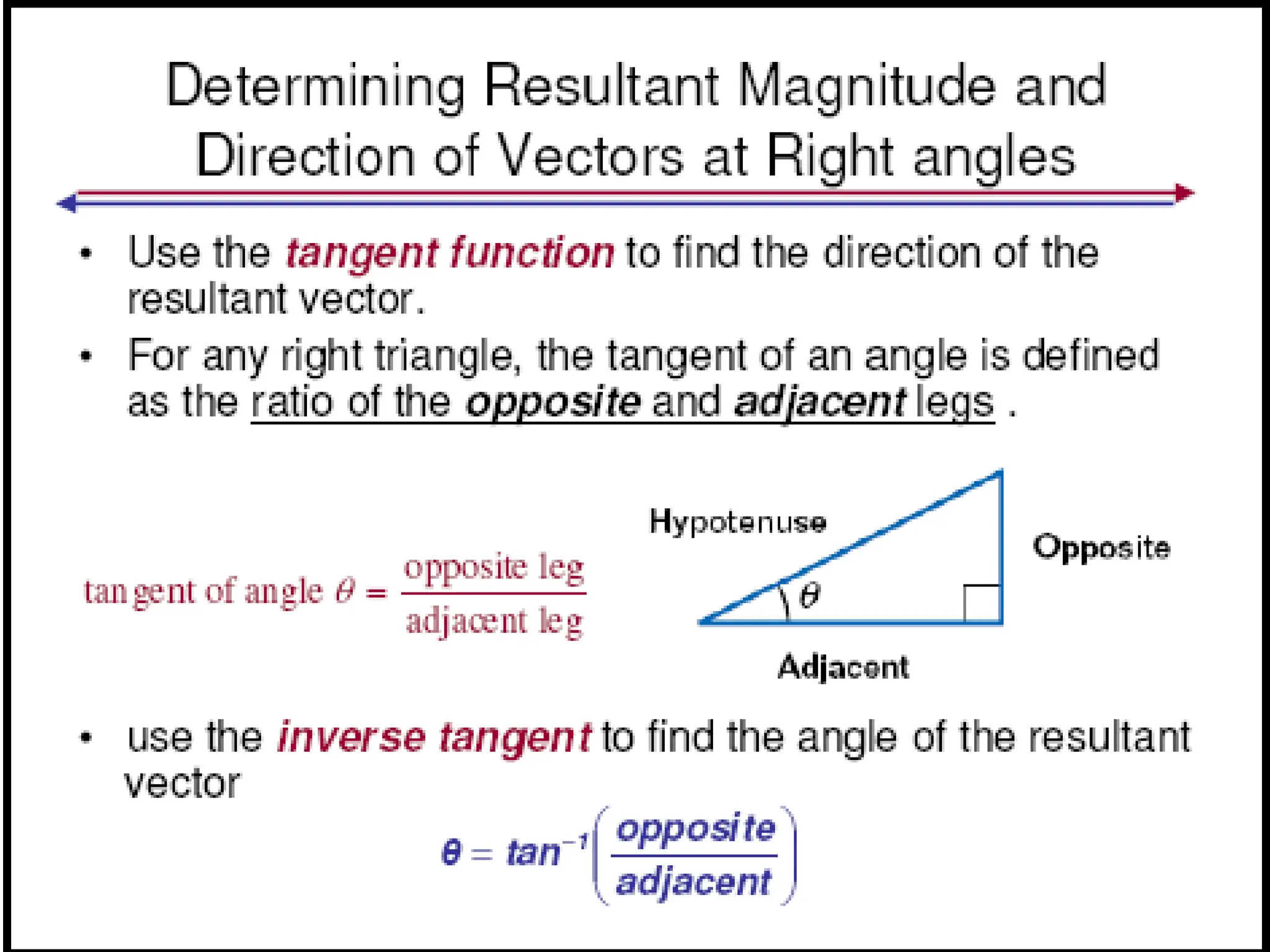
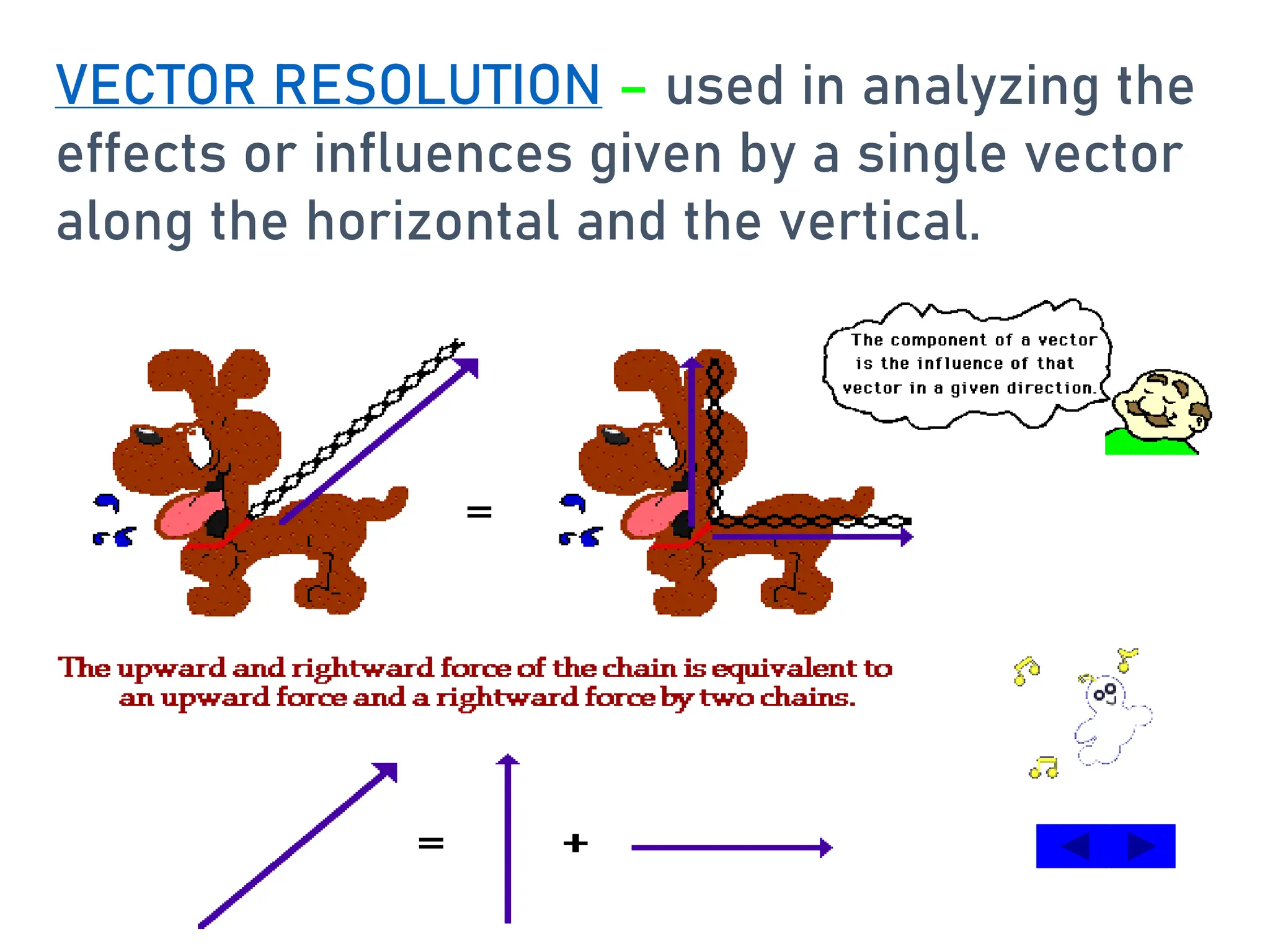
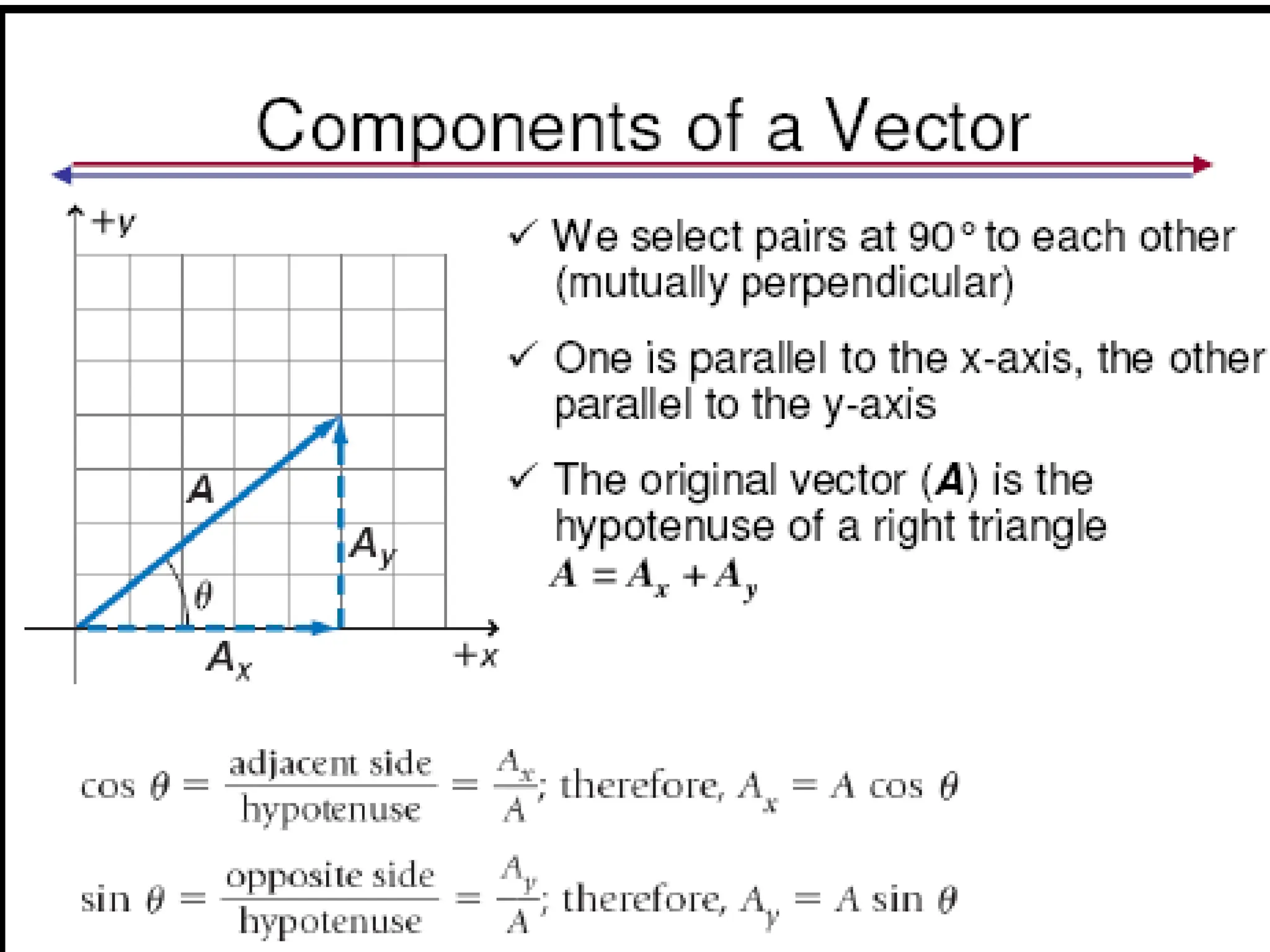
The document outlines methods for vector addition, including cases for both right and non-right angles using the Pythagorean theorem and trigonometric functions. It discusses vector resolution, breaking down vectors into their x and y components, and the significance of these components in terms of direction and effects. Additionally, it includes practice problems and applications involving real-life scenarios for better understanding of vector resolution.

1. Vector
Resolution

2. ANALYTICAL METHOD
OF VECTOR ADDITION
CASE 1: Adding two vectors forming a right
angle (ф = 900)
Use: Pythagorean Theorem – for RMAGNITUDE
Tangent Function – for θ, RDIRECTION,

7. CASE 2: Adding two vectors forming a non-
right angle (ф < or > 900)
USE: Cosine Law - for RMAGNITUDE
Sine Law - for θ, RDIRECTION,
CASE 3: Adding two or more vectors acting
at different angles
USE: Component Method - for RMAGNITUDE
Tangent Function - for θ, RDIRECTION,
ANALYTICAL VECTOR ADDITION

8. VECTOR SUBTRACTION
Vector Subtraction may be indicated as:
d1 – d2 = dR or d1 + ( -d2 ) = dR
+ = + =
d1 d2 d2
d1
d1
d2
dR
•The negative of any vector is a vector of the
same magnitude but points in the opposite
direction.

9. VECTOR RESOLUTION – used in analyzing the
effects or influences given by a single vector
along the horizontal and the vertical.

11. Vector Resolution – is the process of
breaking down a single vector into its two
components (effects or influence given)
along the x- and the y-axis.
• To resolve a vector is NOT to add nor to
subtract a vector.
• The components of the vector, x- & y-
components, are not vector quantities but are
merely scalar. Although they carry + or –
signs, they just show the direction of the
effectivity of given vector along the horizontal
and vertical respects.

12. • The components of a vector are symbolized
and drawn with broken lines with arrowheads
to show the direction of the effect given by a
vector along the horizontal and vertical.
• The x- & y-components of a vector are
indicated as the x- and y-subscript of a given
vector.
• By +x-component means the horizontal effect
of the vector is to the right (or →). By –x, it is
the otherwise.
• By +y-component means the vertical effect of
the vector is upward (or ↑) and by –y
component is the the otherwise.

13. The components of a single vector are:
a. x-component of a vector -i.e., it is the
horizontal effect or horizontal
influence given by a vector in terms
of displacement, velocity or force, etc.
b. y-component of a vector – it is the
vertical effect or influence given by a
vector.

14. How do you resolve a vector analytically?
1. Sketch the vector appropriately and resolve
using triangulation method wherein the angle
given is included in the triangle.
2. The x-component of the vector is the
projection of the vector along the x-axis, i.e., in
either to the left or to the right of the x-axis as
appropriate.
3. The y-component of the vector is the
projection of the vector along the y-axis, i.e., at
either up or down of the y-axis as appropriate.
4. Label your vector components
correspondingly.

16. Applying trigonometric functions in
determining the x- comp of a vector.
1. For the x-comp of a given vector (let stand
for any given vector):
• If the angle is taken from the:
❑ horizontal: Ax = ACosα
❑ Vertical : Ax = ASinα
A




17. 2. For the y-comp of a given vector (let stand
for any given vector):
• If the angle is taken from the:
❑ horizontal: Ay = ASinα
❑ Vertical : Ay = ACosα


A

Applying trigonometric functions in
determining the y-comp of a vector.

19. What is the effect of the
angle that the vector makes
with the horizontal (or vertical)
in terms of its horizontal &
vertical effects respectively?
The Angle of Vector vs. its horizontal &
vertical effects

20. Practice drills:
•Show the components of the following vectors by
naming the vector first, showing complete sketch
for the triangulation method and then solve for
the components analytically. Give meanings for
the components derived. (5min)
1. 100km, 400 West of North
2.75km/h, 560 East of South
3.120N, 370 from the
horizontal

21. Vector Resolution Problems:
•A wind with a velocity of 60 kph
blows in the direction of 420 North of
East of NCR. How much blow of this
wind can be felt by people in the
CAMANAVA area and those in the
Quezon City area?
•When is the wind blow considered to
be a weather
disturbance/depression?

22. Vector Resolution Problems:
2. A hunter climbs a mountain
with a slope tilted 300 from the
horizontal. If the total vertical
ascent is 3km, how far must
the climber walk along the
slope to reach the mountain
top?

23. Vector Resolution Problem:
3. A car weighing 3000lbs is on
a hill that makes an angle of
200 with the horizontal. Find
the components of the car’s
weight parallel and
perpendicular to the road.
Explain the effects given by
the car’s weight as it lies on
the sloped hill.

24. Vector Resolution Problems:
4.A woman pushes a lawn
mower with a force of 20lb.
If the handle of the lawn
mower is 400 above the
horizontal, how much
downward force is being
exerted on the ground?

25. Vector Resolution Problem:
5. An airplane whose airspeed
is 120 kph has just taken off
from a runway. A car driving
at 100kph on the runway is
able to remain just below the
airplane. At what angle is the
airplane climbing?