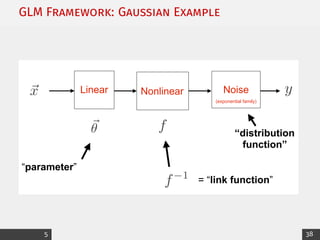
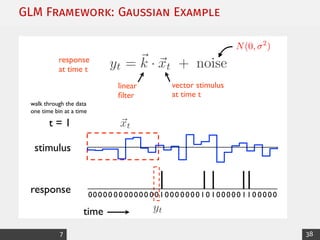
This document provides an overview of generalized linear models (GLMs) and maximum likelihood estimation (MLE). It discusses the exponential family distribution framework for GLMs, which allows the use of the same tools of inference across different distributions. It presents examples of link functions and canonical forms for the Gaussian and Poisson distributions. The document also covers likelihood theory and how to calculate parameter estimates and their uncertainty through taking derivatives of the log-likelihood function. It introduces MLE as a method for finding the parameter values that maximize the likelihood of observing the data. Computational estimation of GLMs is performed through an iterative least squares method using weights from the distributions' Fisher information.

1. Week 2
Generalized Linear Models
Applied Statistical Analysis II
Jeffrey Ziegler, PhD
Assistant Professor in Political Science & Data Science
Trinity College Dublin
Spring 2023

2. Road map for today
Generalized Linear Models (GLMs)
I Why do we need to think like this?
I What type of distributions can we use?
I Getting our parameters and estimates
Next time: Maximum Likelihood Estimation (MLE)
By next week, please...
I Begin working on problem set #1
I Read assigned chapters
This has "been done already", but I want y’all to understand
what’s going on, especially w.r.t. to theory & programming
1 38

3. What are GLMs, why does they matter?
Remember from last week, we want to use same tools of
inference and probability for non-continuous outcomes
So, we need a framework for estimating parametric models:
yi ∼ f(θ, xi)
where:
θ is a vector of parameters
xi is a vector of exogenous characteristics ofith observation
Specific functional form, f, provides an almost unlimited
choice of specific models
I As we will see today, not quite
2 38

4. What do we need to make this work?
For a given outcome, we need to select a distribution (we’ll
narrow down set) and select correct
1. parameter, and
2. estimate
We’ll also want measure of uncertainty (variance)
3 38

5. GLM Framework: Gaussian Example
2. Generalized Linear Model
Linear
Examples: 1. Gaussian
2. Poisson
Noise
(exponential family)
Nonlinear
y = f(~
✓ · ~
x) + ✏
11
4 38

6. GLM Framework: Gaussian Example
2. Generalized Linear Model
Linear Noise
(exponential family)
Nonlinear
Terminology:
“distribution
function”
“parameter”
= “link function”
12
5 38

7. GLM Framework: Gaussian Example
0
0 1
0 0
0 1 0
0 0 0 0 0 1 0
1
01
0 0 0 00
0 0 0 0
0 0 0
0 0
0
0 0
0 0
stimulus
response
From s ike counts to spike trains:
linear
filter
vector stimulus
at time t
time
response
at time t
first idea: linear-Gaussian model!
yt = ~
k · ~
xt + ✏t
yt = ~
k · ~
xt + noise
N(0, 2
)
13
6 38

8. GLM Framework: Gaussian Example
~
xt
yt
0
0 1
0 0
0 1 0
0 0 0 0 0 1 0
1
01
0 0 0 00
0 0 0 0
0 0 0
0 0
0
0 0
0 0
stimulus
response
linear
filter
vector stimulus
at time t
yt = ~
k · ~
xt + noise
time
response
at time t
t = 1
walk through the data
one time bin at a time
N(0, 2
)
14
7 38

9. GLM Framework: Gaussian Example
~
xt
yt
0
0 1
0 0
0 1 0
0 0 0 0 0 1 0
1
01
0 0 0 00
0 0 0 0
0 0 0
0 0
0
0 0
0 0
linear
filter
vector stimulus
at time t
yt = ~
k · ~
xt + noise
time
response
at time t
t = 2
walk through the data
one time bin at a time
stimulus
response
N(0, 2
)
15
8 38

10. GLM Framework: Gaussian Example
~
xt
yt
0
0 1
0 0
0 1 0
0 0 0 0 0 1 0
1
01
0 0 0 00
0 0 0 0
0 0 0
0 0
0
0 0
0 0
linear
filter
vector stimulus
at time t
yt = ~
k · ~
xt + noise
time
response
at time t
t = 3
walk through the data
one time bin at a time
stimulus
response
N(0, 2
)
16
9 38

11. More familiar maybe in matrix version
Build up to following matrix version:
0
…
Y X~
k
= + noise
=
time
design matrix
…
~
k
1
0
10 38

12. More familiar maybe in matrix version
Build up to following matrix version:
0
1
0
…
Y X~
k
= + noise
=
time
k̂ = (XT
X) 1
XT
Y
stimulus
covariance
spike-triggered avg
(STA)
(maximum likelihood estimate for
“Linear-Gaussian” GLM)
least squares solution:
…
~
k
21
11 38

13. Towards a likelihood function
12 38

14. Towards a likelihood function
Formal treatment: scalar version
model:
N(0, 2
)
yt = ~
k · ~
xt + ✏t
equivalent to writing: yt|~
xt,~
k ⇠ N(~
xt · ~
k, 2
)
p(yt|~
xt,~
k) = 1
p
2⇡ 2
e
(yt ~
xt·~
k)2
2 2
or
p(Y |X,~
k) =
T
Y
t=1
p(yt|~
xt,~
k)
For entire dataset:
(independence
across time
bins)
= (2⇡ 2
)
T
2 exp(
PT
t=1
(yt ~
xt·~
k)2
2 2 )
Guassian noise
with variance 2
log P(Y |X,~
k) =
PT
t=1
(yt ~
xt·~
k)2
2 2 + const log-likelihood
22
13 38

15. Towards a likelihood function
Formal treatment: vector version
0
…
Y X~
k
=
…
~
k
=
time
+ ~
✏
N(0, 2
I)
…
+
iid Gaussian
noise vector
✏1
✏2
✏3
equivalent to writing:
or
Y |X,~
k ⇠ N(X~
k, 2
I)
P(Y |X,~
k) = 1
|2⇡ 2I|
T
2
exp
⇣
1
2 2 (Y X~
k)>
(Y X~
k)
⌘
Take log,
differentiate and
set to zero.
1
0
23
14 38

16. Towards a likelihood function
15 38

17. Towards a likelihood function
0
…
…
~
k
≈
time
probability of
spike at bin t
Bernoulli GLM: pt = f(~
xt · ~
k)
(coin flipping model,
y = 0 or 1)
p(yt = 1|~
xt) = pt
nonlinearity
Equivalent ways of writing: yt|~
xt,~
k ⇠ Ber(f(~
xt · ~
k))
p(yt|~
xt,~
k) = f(~
xt · ~
k)yt
⇣
1 f(~
xt · ~
k)
⌘1 yt
or
But noise is not Gaussian!
log-likelihood: L =
PT
t=1
⇣
yt log f(~
xt · ~
k) + (1 yt) log(1 f(~
xt · ~
k))
⌘
f( )
1
0
16 38

18. GLM Framework: Logit too!
Logistic regression
Logistic regression: f(x) =
1
1 + e x
logistic function
• so logistic regression is a special case of a Bernoulli GLM
0
…
…
~
k
≈
time
probability of
spike at bin t
Bernoulli GLM: pt = f(~
xt · ~
k)
(coin flipping model,
y = 0 or 1)
p(yt = 1|~
xt) = pt
nonlinearity
f( )
1
0
25
17 38

19. Where to start? Exponential Family Intro
We need to narrow down set of functions
I Set we use is called ’exponential family form’ (EFF), which we
can characterise in ’canonical form’
Nice properties:
I All have "their moments"
We should be able to characterise (1) center and (2) spread of
data generating distribution based on data
More specifically, by putting PDFs and PMFs into EFF, we are
able to isolate subfunctions that produce a small # of statistics
that succinctly summarize large data using a common notation
Exceptions: Student t’s or uniform distributions can’t transform
into EFF, they’re dependent on bounds (sometimes Weibull)
I Allows us to use log-likelihood functions in replace of
likelihood function because they have same mode (maximum
of function) for θ
18 38

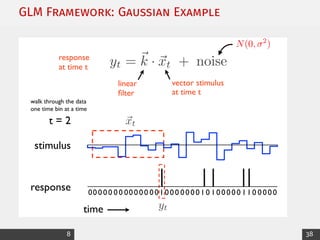
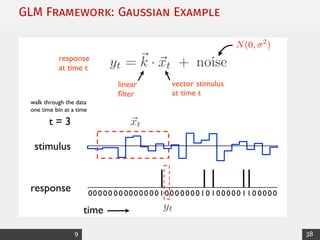
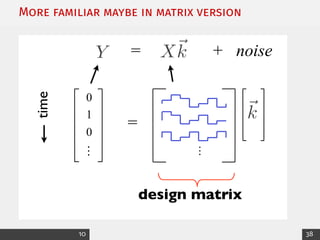
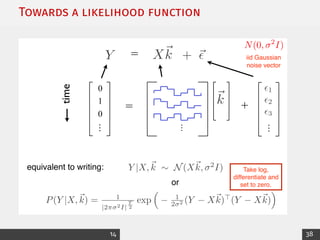
20. Exponential Family: Canonical Form
The general expression is
f(y|θ) = exp[yθ − b(θ) + c(y)]
where
yθ multiplicative term have both y and θ
b(θ) ’normalising constant’
We want to isolate and derive b(θ)!
19 38

21. Next, construct joint distribution
This is important, we need this for likelihood function
f(y|θ) = exp
" n
X
yiθ − nb(θ) +
n
X
c(yi)
#
20 38

22. Example: Poisson
f(y|µ) =
e−µµy
y!
= e−µ
µy
(y!)−1
(1)
Let’s take log of expression, place it within an exp[]
= exp [−µ + ylog(µ) − log(y!)]
= exp [ylog(µ) − µ − log(y!)]
(2)
where
yθ ylog(µ)
b(θ) µ
c(y) log(y!)
21 38

23. Example: Poisson
yθ ylog(µ)
b(θ) µ
c(y) log(y!)
In canonical form, θ = log(µ) = canonical link
Parameterized form of b(θ) by θ is done by taking inverse of
canonical link whereby b(θ) = exp(θ) = µ
22 38

24. Likelihood Theory
Awesome, we have a way to calculate our parameters of
interest, now what?
How do we calculate our estimates?
For sufficiently large samples, likelihood surface is unimodal
in k dimensions for exponential forms
I Process is equivalent to finding a k-dimensional mode
I We want a posterior distribution of unknown k-dimensional θ
coefficient vectors given observed data, f(θ|X)
23 38

25. Likelihood Theory
f(θ|X) = f(X|θ)
p(θ)
p(X)
where
f(X|θ) represents the joint PDF
p(θ) is posterior produced by Bayes rule
p(X) is unconditional probabilities
Determines the most likely values of a θ vector
24 38

26. Likelihood Theory
We can regard f(X|θ) as a function for θ given observed data,
where p(X) = 1 since we observed data
We then stipulate a prior distribution of θ to allow for a
direct comparison of observed data versus prior
Gives us our likelihood function, L(θ|X) = f(X|θ), where we
want to find value of θ that maximises likelihood function
25 38

27. Likelihood Theory
If θ̂ is estimate of θ that maximizes the likelihood function,
then L(θ̂|X) ≥ L(θ|X)∀θ ∈ Θ
To get expected value of y, E[y], we first need to differentiate
b(θ) with respect to θ whereby ∂
∂θ b(θ) = E[y]
We can follow these steps:
1. Take ∂
∂θ b(θ)
2. Insert canonical link function for θ
3. Obtain θ̂
26 38

28. Likelihood Theory
To get uncertainty estimate of θ̂ (its variance), we can take
the second derivative of b(θ) with respect to θ such that
∂2
∂θ2 b(θ) = E[(y − E[y])2]
We can then re-write the variance as1
1
a2(ψ)
var[y] → var[y] = a(ψ)
∂2
∂θ2
b(θ)
1
It’s useful to re-write canonical form to include a scale parameter, a(ψ). When a(ψ) = 1, then ∂2
∂θ2 b(θ) is
unaltered, (y|θ) = exp[
yθ−b(θ)
a(ψ)
+ c(y, ψ).
27 38

29. Likelihood Theory Ex: Poisson
We will also use canonical equation that includes a scale
parameter for Poisson
We know that inverse of canonical link gives us
b(θ) = exp[θ] = µ, which we will insert in
exp [ylog(µ) − µ − log(y!)] (3)
a(ψ)
∂2
∂θ2
b(θ) = 1
∂2
∂θ2
expθ|θ= log(µ)
= exp(log(µ))
θ̂ = µ
(4)
28 38

30. Notation side note: ∝ versus =
As Fisher defines it, likelihood is proportional to joint
density of data given parameter value(s)
I This is important in distinguishing likelihood from inverse
probability or Bayesian approaches
I However, “likelihood function” that we maximize is equal to
joint density of data
When talking about a likelihood function that will be
maximized, we’ll use L(θ|y) =
Q
f(y|θ) from now on
I But we’ll remember that proportionality means we can only
compare relative sizes of likelihoods
I Value of likelihood has no intrinsic scale and so is essentially
meaningless except in comparison to other likelihoods
29 38

31. From parameter to estimate: Link Functions
We have essentially created a dependency connecting linear
predictor and θ (via µ in our Poisson example)
We can begin by making a generalization where V = Xβ + e
such that V represents a stocastic component, X denotes
model matrix, and β are estimated coefficients
We can then denote expected value as a linear structure,
E[V] = θ = Xβ
30 38

32. From parameter to estimate: Link Functions
Let’s now imagine that expected value of stocastic
component is some function, g(µ) that is invertible
Information from explanatory variables is now expressed
only through link (Xβ) to linear predictor, θ = g(µ), which is
controlled by link function, g()
We can then extend Generalized linear model to accomodate
non-normal response functions by transforming functions
linearly
This is achieved by taking inverse of link function, which
ensures Xβ̂ maintains linearity assumption required of
standard linear models
g−1
(g(µ)) = g−1
(θ) = g−1
(Xβ) = µ = E[Y]
31 38

33. Basics of MLE: Setup
Begin with likelihood function
Function of parameters that represents probability of
witnessing observed data given value of parameter
Likelihood function : P(Y = y) =
Y
f(yi|θ) = L(yi|θ)
32 38

34. Basics of MLE: Setup
Awesome, and...? So far, we have a way to think about
I Which distributions we want to work with
I How to characterise center & spread
I Link data to those moments
I Now, we need a way to actually calculate our estimates
33 38

35. Basics of MLE: Setup
Maximum likelihood estimate (MLE) is value of parameter
that gives largest probability of observing data
I Score function u(θ) is derivative of log-likelihood function
with respect to the parameters
I Fisher information var(u(θ)) measures uncertainty of
estimate, θ̂
I To find Fisher information, take second derivative of
likelihood function
34 38

36. Basics of MLE: Computational Estimation
MLE is typically found by using Newton-Raphson method,
which is an iterative process of mode finding
I More on this next week!
We begin by estimating k-dimensional β̂ estimates by
performing an iterative least squares method with diagonal
elements of an A matrix of weights
These diagonal element are typically Fisher information of
exponential family distribution
35 38

37. Wrap-up
What is exponential family form?
What is a link function?
Why are we performing MLE?
36 38

38. Next week
Unfortunately there isn’t a closed form solution for β (except
in very special cases)
Newton-Raphson method is an iterative method that can be
used instead
Computationally convenient to solve on each iteration by
weighted least squares
37 38

39. Class business
Read required (and suggested) online materials
Problem set # 1 is up on GitHub
Next time, we’ll talk about how to actually maximise our
likelihood functions !
38 / 38