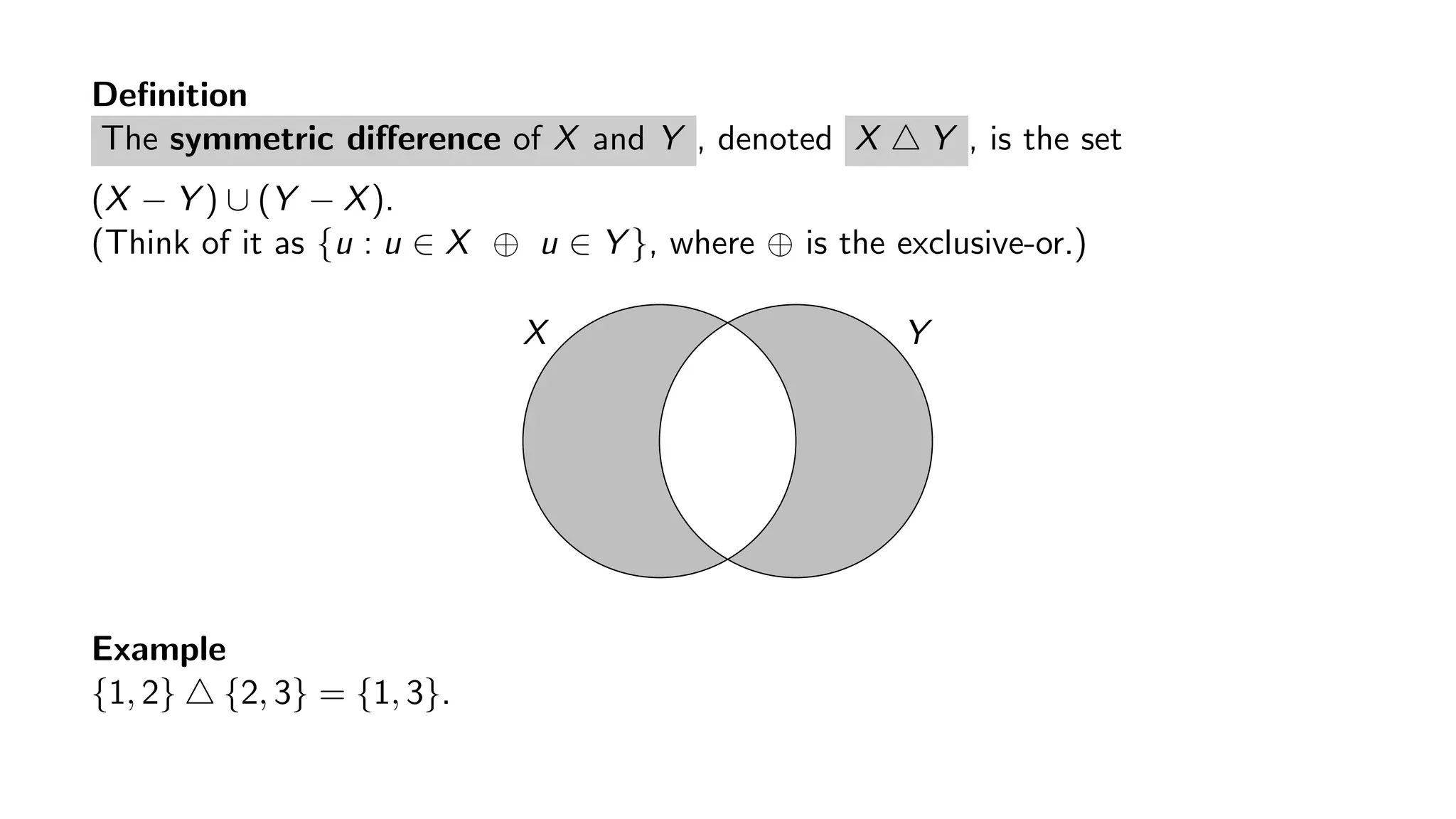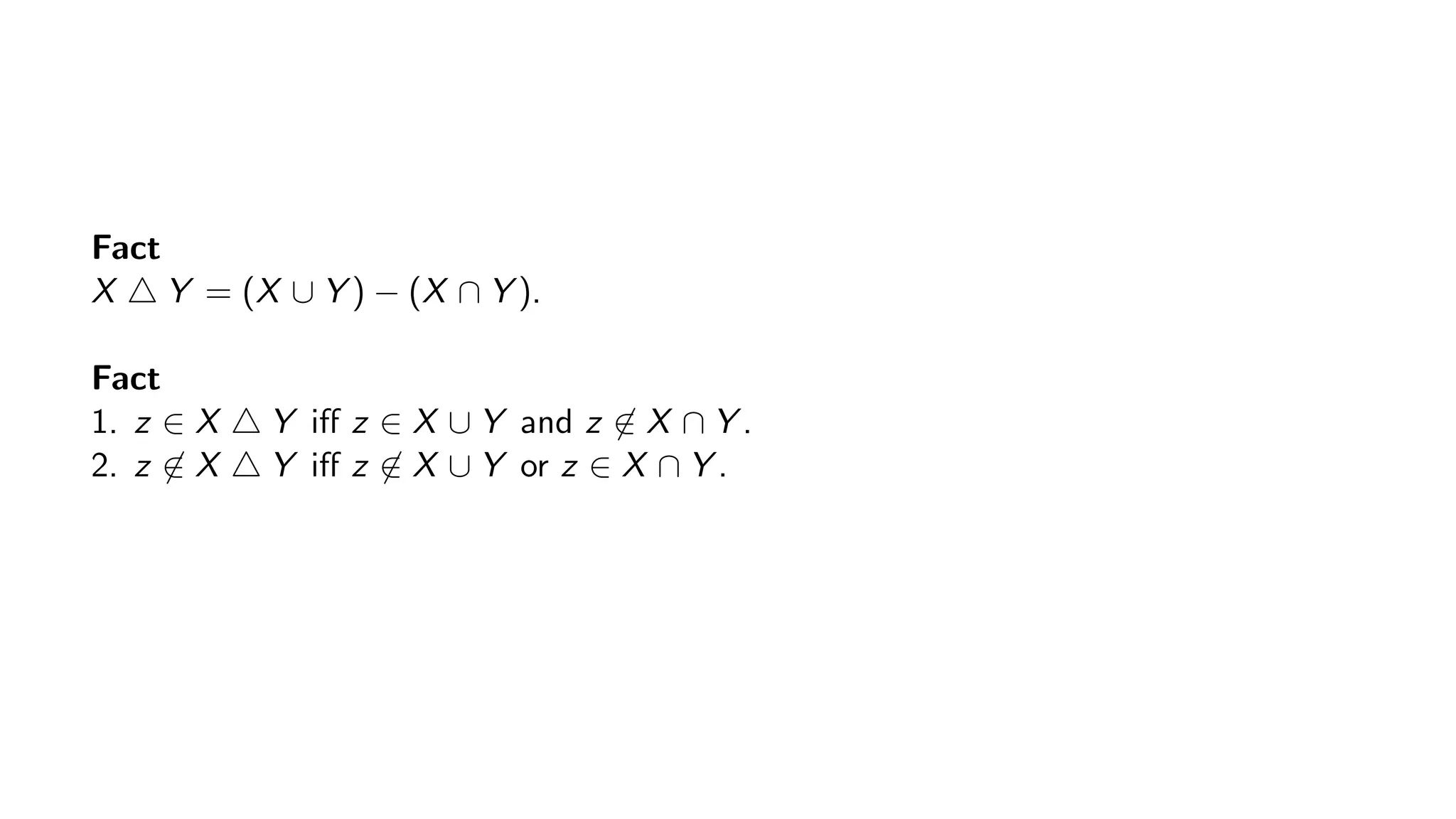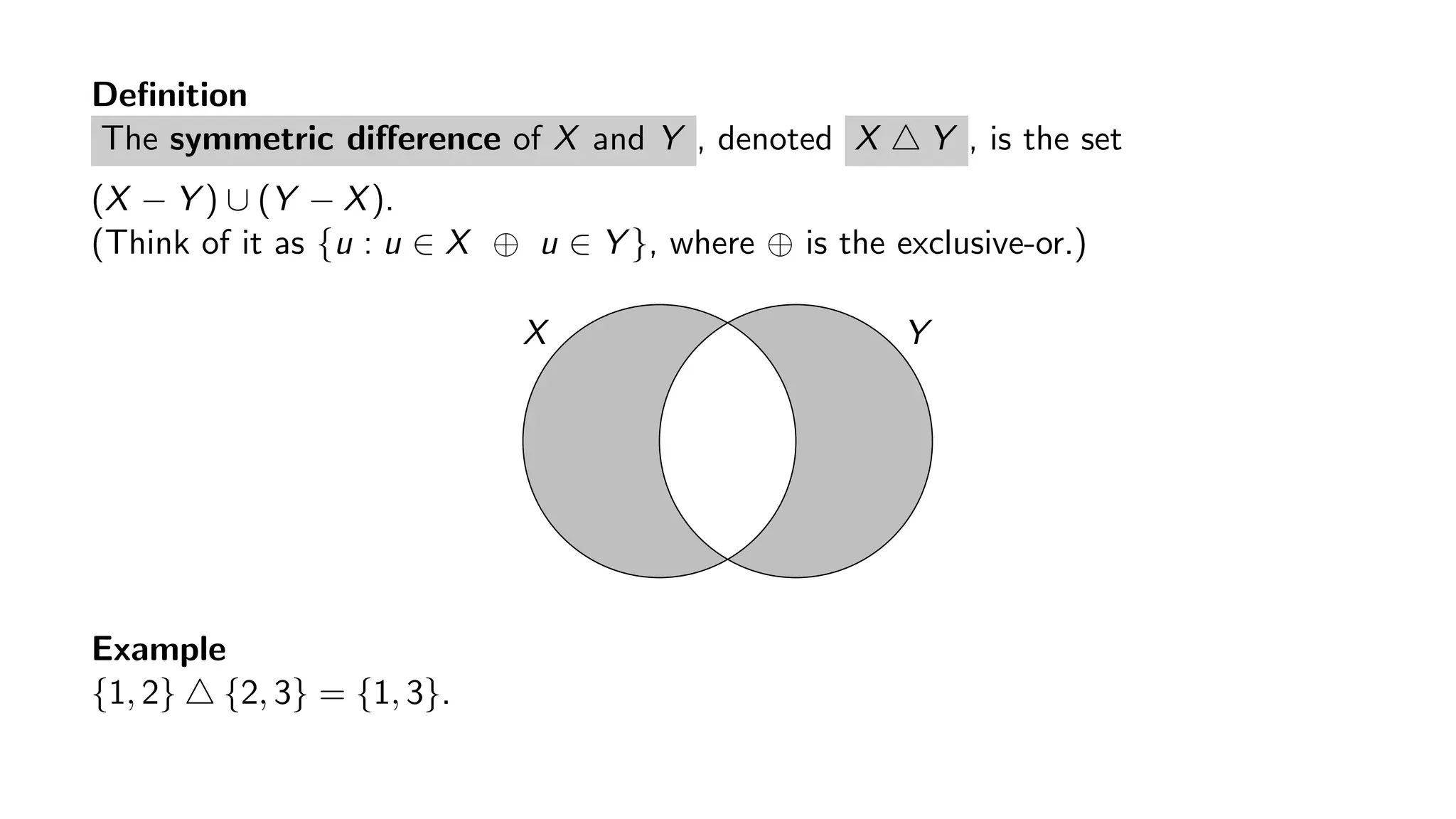
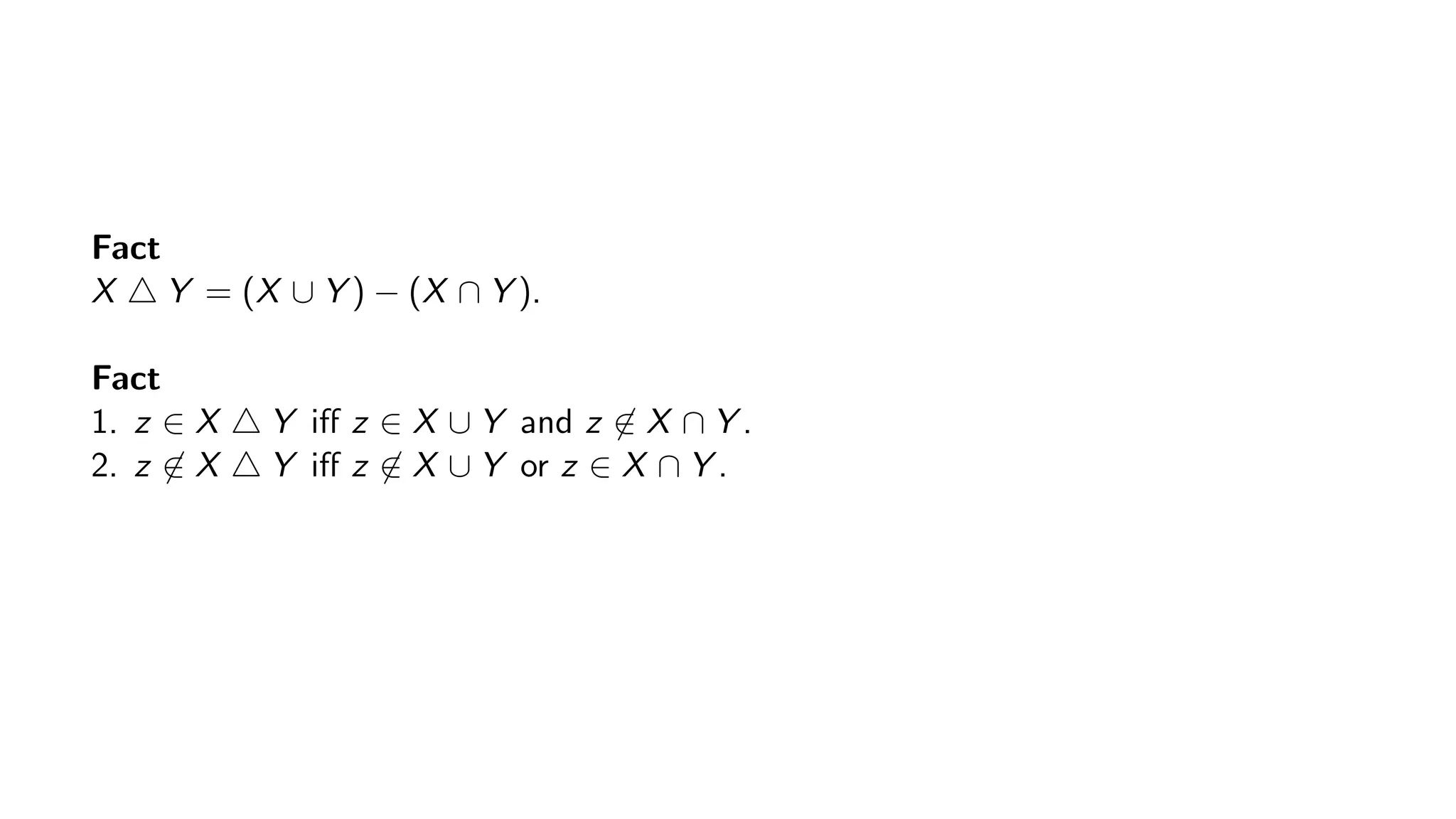
The document introduces the concept of symmetric difference in set theory, defined as the set of elements that are in either of two sets but not in their intersection. It provides a formal definition, examples, and facts relating to the symmetric difference, as well as implementation strategies using dynamic hash tables and bitwise operations. Additionally, the document includes exercises for further understanding of the symmetric difference and its properties.

1. Introduction to set theory and to methodology and philosophy of
mathematics and computer programming
Symmetric difference
An overview
by Jan Plaza
c 2017 Jan Plaza
Use under the Creative Commons Attribution 4.0 International License
Version of February 6, 2017

2. Definition
The symmetric difference of X and Y , denoted X Y , is the set
(X − Y ) ∪ (Y − X).
(Think of it as {u : u ∈ X ⊕ u ∈ Y }, where ⊕ is the exclusive-or.)
X Y
Example
{1, 2} {2, 3} = {1, 3}.

3. Fact
X Y = (X ∪ Y ) − (X ∩ Y ).
Fact
1. z ∈ X Y iff z ∈ X ∪ Y and z ∈ X ∩ Y .
2. z ∈ X Y iff z ∈ X ∪ Y or z ∈ X ∩ Y .

4. Implementation
1. As X Y = (X − Y ) ∪ (Y − X),
with sets implemented as dynamic hash tables,
symmetric difference can be defined in terms of union and set-difference.
2. As z ∈ X Y iff z ∈ X ⊕ z ∈ Y ,
with bit-array implementation of sets,
one can use the bitwise exclusive-or (xor) operation, often denoted by ^.

5. Exercise
1. X ∅=...
2. X U =...
3. X X =...
4. X Xc =...
Exercise
Complete:
1. (X ∪ Y ) − (X ∩ Y )=...
2. (X ∩ Y ) ∪ (X Y )=...
3. (X − Y ) ∪ (Y − X)=...

6. Exercise
1. X ⊆ Y iff X Y =...
2. X ⊆ Y iff X Y c =...
3. X ⊆ Y iff Xc Y =...
4. X ⊆ Y iff Xc Y c =...