Dokumen ini membahas berbagai aspek logika, termasuk pernyataan, jenis logika (deduktif dan induktif), serta metode penarikan kesimpulan seperti modus ponen, modus tolen, silogisme dan dilema. Diberikan juga penjelasan mengenai pernyataan tunggal dan majemuk, nilai kebenaran, serta kata hubung logika. Contoh-contoh aplikasi logika dalam bentuk pernyataan dan kesimpulan juga disertakan untuk ilustrasi.

1. Logika

2. Logika: Cara berpikir
• Logika tradisional
• Logika Simbolik
• Logika Induktif
• Logika Deduktif

3. Kalimat
• Pernyataan
• Bukan pernyataan

4. Pernyataan:
• Berita: Pasti nilai kebenarannya
• Nama lain: deklaratif, proposisi, statemen
• Dilambangkan dengan huruf kecil (p,q,r,s)
• Nilai kebenarannya dilambangkan B (Benar)
atau T (True) dan S (Salah) atau F (False)

5. Bukan Pernyataan:
• Pertanyaan, perintah
• Berita: Tidak pasti nilai
kebenarannya

6. Pernyataan / Bukan Pernyataan?
• Matahari terbit dari
timur
• 2 + 5 = 6
• Manusia merupakan
makhluk hidup
• 2+y=1 maka y= -1
• Tidak ada bilangan
ganjil yang habis
dibagi dua.
• Soto rasanya enak
• Kopinya terlalu manis
• Suamiku kaya
• Sebentar lagi
perkuliahan selesai
• Jakarta lebih jauh
daripada Surabaya
• 5 – x = 3
• 2x + 3y > 10
• Siapa namamu?
• Bacalah dengan
cepat!
• Jangan menggang-
gu teman!
• Kerjakan dengan
teliti!
BUKAN PERNYATAAN
PERNYATAAN

7. Macam Pernyataan
• Pernyataan Tunggal:
(Satu pernyataan)
• Pernyataan Majemuk
(Gabungan beberapa pernyataan)
• Kata hubung logika: DAN, ATAU,
JIKA … MAKA, JIKA DAN
HANYA JIKA

8. Contoh Pernyataan Tunggal
• 2 + 5 = 7
• Harimau termasuk karnivora
• Bulan merupakan sumber cahaya
• 3 – 4 = 7
• Tidak benar bahwa 2 adalah bilangan ganjil
• Ada hewan berkaki lebih dari 7
• Tidak semua bersinar disebut sebagai
sumber cahaya
• 6 : 3 > 2
• Semua bilangan prima adalah ganjil

9. Contoh Pernyataan Majemuk
Wati dan Nina pergi kuliah
Besok siang saya ke luar kota atau mengajar UT
Kamu saya lamar jika saya sudah bekerja
3 + 5 > 2 atau 3 + 5 < 10
Buku satu-satunya alat tulis dan semua makhluk
hidup bernafas
Salatiga ada di tepi pantai jika dan hanya jika 2
bilangan ganjil
Jika 5 bilangan genap maka harimau makan
rumput

10. Kalimat Terbuka
Belum diketahui kebenarannya
Terdapat variabel (peubah)
Kegiatan mengganti variabel dengan konstanta
(tetapan) tertentu = menentukan penyelesaian
Pengganti variabel berupa himpunan selesaian
Contoh:
3 + x = 8
2x = 5
6x – 2 y < 5

11. Operasi Pernyataan dan
Nilai Kebenarannya
• Dan (Konjungsi)
• Atau (Disjungsi)
• Negasi (ingkaran)
• Jika … maka (implikasi)
• …. jika dan hanya jika … (biimplikasi)

12. KONJUNGSI
• Kata hubungnya DAN

• Lambangnya
• Bernilai Benar jika seluruh pernyataan bernilai
benar

13. DISJUNGSI
• Kata hubungnya ATAU

• Lambangnya
• Bernilai Salah jika seluruh pernyataan bernilai
Salah

14. NEGASI
• INGKARAN (Mengingkari kebenaran yang ada)
p
atau
p
~
• Lambangnya
• Nilainya berlawanan

15. IMPLIKASI
• Pernyataan bersyarat
....
.... 
• Lambangnya
• Jika …. Maka …. Atau …. Jika ….
q
p
• Contoh
• Jika p Maka q Atau q Jika p
• p prasyarat q
• Bernilai Salah jika prasyarat BENAR diikuti
pernyataan bernilai Salah

16. BI-IMPLIKASI
• Pernyataan bersyarat ganda
....
.... 
• Lambangnya
• …. Jika dan hanya jika ….
q
p
• Contoh
• p jika dan hanya jika q
• p prasyarat q dan q prasyarat p
• Bernilai BENAR jika nilai kebenaran
KEDUANYA SAMA.
p
q
q
p 



17. q
p p
q
q
p 



p q p q q  p (pq)^(qp) q
p

18. Nilai Kebenarannya
Pernyataan Ganda
• Kontradiksi
• Tautologi
• Kontingensi
• Ekuivalensi

19. p ~p pv~p p^~p p~p ~pp p
p ~


20. p q ~p ~q pq ~p~q qp ~q~p

21. q
p p
q 
q
p ~
~  p
q ~
~ 
INVERS
INVERS
KONVERS
KONVERS

22. 

Pernyataan Berkuantor:
Kuantor Universal:
• Untuk semua
•Tanpa kecuali
•Jika bisa menemukan 1 saja
yang dapat menggagalkan
maka pernyataan menjadi salah
Kuantor Eksistensial
Ada.
Paling sedikit 1

23. Benarkah penarikan
kesimpulan di bawah ini?
• Jika orang Salatiga maka tahu lapangan
pancasila. Amir bukan orang Salatiga maka
ia tidak mengenal lapangan pancasila
• Jika ia mahasiswa UT maka maka rajin
membaca. Amir rajin membaca jadi ia
mahasiswa UT.
• Jika guru TK maka selalu berpakaian rapih.
Wati selalu tidak berpakaian rapih, jadi ia
bukan guru TK.
• Jika pelanggan puas ia akan datang lagi.
Anton berkunjung dan tidak datang lagi, jadi
ia tidak puas.
• Jika bayi minum ASI maka ia sehat. Upik
tidak minum ASI jadi ia tidak sehat.

24. Penarikan Kesimpulan
• Penarikan kesimpulan
dikatakan sah apabila
diperoleh suatu tautologi
• Beberapa istilah:
Premis = Pernyataan
Konklusi = Kesimpulan

25. Metode
Penarikan Kesimpulan
 Modus PONEN
 Modus TOLEN
 SILOGISME
 Dilema

26. MODUS PONEN
• Pernyataan majemuk implikasi dengan diikuti
pernyataan tunggal benar sebagai prasyarat
implikasi.
Premis 1 p  q (suatu pernyataan yang benar)
Premis 2 p (suatu pernyataan bernilai benar)
Konklusi q ( suatu pernyataan yang bernilai benar)
  q
p
q
p 

 )
(

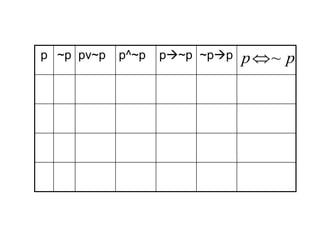
27. p q pq (pq)^p [(pq)^p]  Q
Tabel Kebenaran MODUS PONEN

28. Contoh penarikan kesimpulan
dengan MODUS PONEN
• Jika orang Salatiga maka tahu lapangan
pancasila. Amir orang Salatiga. Jadi ia tahu
lapangan pancasila
• Jika ia mahasiswa UT maka maka rajin
membaca. Amir mahasiswa UT. Amir rajin
membaca.
• Jika guru TK maka selalu berpakaian rapih.
Wati guru TK, maka Wati selalu berpakaian
rapih.
Premis 1
Premis 2
Konklusi

29. Contoh penarikan kesimpulan
dengan MODUS PONEN
Premis 1 Jika suatu bilangan habis dibagi 2
maka bilangan itu genap.
Premis 2 100 habis dibagi 2
Konklusi ………………………………..
Premis 1 Jika bulan purnama maka air laut
pasang
Premis 2 Sekarang tanggal 15 bulan
komariah
Konklusi ………………………………..

30. MODUS TOLEN
• Bentuk kontrapositip dari pernyataan pertama
Premis 1 p  q (benar)
Premis 2 ~q (benar)
Konklusi ~p (benar)
  p
q
q
p ~
~
)
( 



31. p q pq (pq)^~q [(pq)^~q]  ~p
Tabel Kebenaran MODUS TOLEN

32. Contoh penarikan kesimpulan
dengan MODUS TOLEN
• Jika naik kelas Ari dibelikan sepeda. Ari tidak
dibelikan sepeda. Jadi Ari tidak naik kelas
• Jika suatu bilangan kelipatan 6 maka
bilangan itu kelipatan 3. 100 bukan kelipatan
3. Maka100 bukan kelipatan 6.
• Jika guru TK maka selalu berpakaian rapih.
Wati tidak pernah perpakaian rapih, jadi
pastilah Wati bukan guru TK.
Premis 1
Premis 2
Konklusi

33. Contoh penarikan kesimpulan
dengan MODUS TOLEN
Premis 1 Jika suatu bilangan habis dibagi 2
maka bilangan itu genap.
Premis 2 7 tidak habis dibagi 2
Konklusi ………………………………..
Premis 1 Carnivora hewan pemakan daging
Premis 2 Sapi pemakan tumbuhan
Konklusi ………………………………..

34. SILOGISME
• Silogisme Disjungtif: Jika diberi 2 pilihan
pernyataan dengan kata hubung ATAU.
Kenyataan yang ada tidak memilih yang
salah satu, pastilah yang terjadi yang
lainnya.
• Silogisme Hipotetis: Pernyataan
kebenaran berantai.

35. SILOGISME DISJUNGTIF
• Silogisme Disjungtif: Jika diberi 2 pilihan
pernyataan dengan kata hubung ATAU.
Kenyataan yang ada tidak memilih yang
salah satu, pastilah yang terjadi yang
lainnya.
 
  q
p
q
p 

 ~

36. p q p v q (p v q)^~p (p v q)^~p]  q
Tabel Kebenaran Silogisme Disjungtif

37. Contoh penarikan kesimpulan
dengan Silogisme Disjungtif
• Hari libur saya tidur siang atau jalan-jalan.
Hari ini hari libur dan saya tidak tidur siang.
Jadi saya jalan-jalan
• Setiap kuliah ia selalu memakai baju biru
atau ungu. Kuliah hari ini ia tidak memakai
baju ungu. Pastilah ia memakai baju biru.

38. Contoh penarikan kesimpulan
dengan Silogisme Disjungtif
Premis 1 Sarapan saya roti atau nasi.
Premis 2 Pagi ini saya tidak makan roti
Konklusi ………………………………..

39. SILOGISME HIPOTESIS
• Penarikan kesimpulan kebenaran
berantai.
   
   
r
p
r
q
q
p 





40. Tabel Kebenaran Silogisme Hipotesis
p q r pq qr (pq)^(qr) pr [(pq)^(qr)]r

41. Contoh penarikan kesimpulan
dengan Silogisme Hipotesis
• Jika bayi minum ASI maka ia sehat
• Jika bayi sehat maka perkembangan
otaknya bagus
• Adi minum ASI jadi perkembangan otaknya
bagus

42. Contoh penarikan kesimpulan
dengan Silogisme Hipotesis
Premis 1 Jika suatu bilangan kelipatan 100 maka ia
adalah genap
Premis 2 Jika bilangan genap maka ia kelipatan 2
Konklusi ………………………………..

43. DILEMA
• Pernyataan disjungsi
• Kedua pernyataan menjadi penyebab
munculnya kejadian baru
• Pastilah kejadian itu benar terjadi
     
 
  r
r
q
r
p
q
p 






44. Tabel Kebenaran DILEMA
p q r pvq pr qr (pvq)^ (pr)^ (qr) [(pvq)^ (pr)^ (qr)]r

45. Contoh penarikan kesimpulan
dengan DILEMA
• Besok saya berenang atau badminton
• Jika saya berenang saya gembira
• Jika saya badminton saya gembira
• Jadi besok saya gembira

46. Contoh penarikan kesimpulan
dengan dilema
Premis 1 Air limbah kotor atau berbau
Premis 2 Jika air kotor maka tidak sehat
Premis 3 Jika air berbau maka tidak sehat
Konklusi ………………………………..