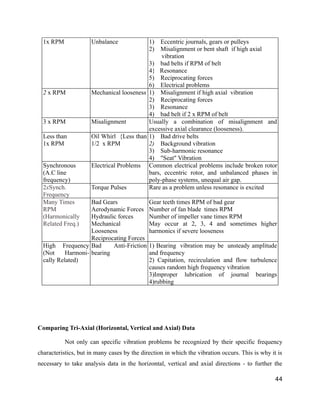
The document provides information on performing vibration analysis of machinery. It discusses defining the problem to be analyzed, determining machine details, performing a visual inspection including slow motion studies, probing studies to identify vibration in other system components, and obtaining vibration spectra at machine bearings. The goal is to identify the problem component and reduce the list of possible causes by analyzing the vibration frequencies and their relationship to machine rotational speeds.