This document discusses a semantic segmentation method for pedestrian trajectories using a combination of Mixture Model of Dynamic pedestrian Agents (MDA) and Hidden Markov Models (HMM). It focuses on enhancing trajectory classification by integrating human behavior models and evaluating its effectiveness against traditional methods. Results indicate improved segmentation accuracy on both synthetic and real datasets compared to baseline techniques.

1. Classification and segmentation of pedestrian trajectories
Toru Tamaki, Hiroshima University
Joint work with Daisuke Ogawa, Bisser Raytchev, Kazufumi Kaneda
7
Semantic segmentation
by models of human behavior
• Models of human behavior by Bayesian inference
• Hidden Markov Model (HMM)
(MDA)

2. 8
Results of semantic segmentation
based on destinations and walking speeds
(Length of arrows)(Direction of arrows)
(Colors)

3. Background 9
¡ Trajectory prediction
¡ Abnormal behavior detection ¡ Crowd behavior analysis
[Zhou+, IJCV2015] [Lee+,CVPR2017]
[Saligrama+,CVPR2012] [Solmaz+,PAMI2012]
¡ Trajectory classification

4. Related work
¡ TRAOD [Lee+, ICDE2008]
¡ Trajectory outlier detection
¡ Segmentation by MDL as preprocessing
¡ Transportation Mode [Zheng+, ACM WWW2008]
¡ Estimation of Transportation Mode (Walk, Car Bus, Bike)
from GPS data
¡ Semantic segmentation based on Transportation Mode
10
No segmentation methods
based on human behavior
(Minimum Description Length)

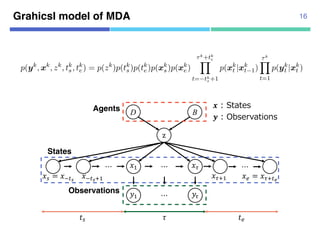
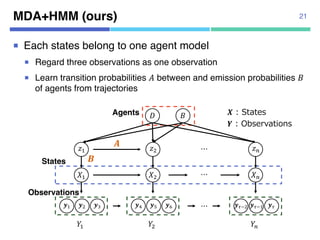
5. Proposed method (MDA+HMM)
¡ Extend classification method to semantic segmentation
by combining with Hidden Markov Model
11
Models of human behavior (or agents) Parameter estimation
Pedestrian trajectory Semantic segmentation
MDA+HMM
MDA
[Zhou+, IJCV2015]
HMM
[Baum, 1972]
[Viterbi, 1967]
!" !# !$ !% !& !' !()# !()" !(⋯
+" +# +,
-" -# -,⋯
. /Agents
Observations
0" 0# 0,⋯
States
1
2
3
4

6. MDA: Mixture model of Dynamic pedestrian-Agents
¡ Example : Input trajectories (blue) and two agent models
12
[Zhou+, IJCV2015]

7. MDA (Mixture model of Dynamic pedestrian-Agents)
¡ Initialize LDS and Gaussian distributions
13
start
goal
start goalD
D
[Zhou+, IJCV2015]
B
B
B
B
Agents have D and B respectively
• D (dynamics) : Linear dynamic system
• B (belief) : Gaussian distributions
(start, goal)

8. MDA (Mixture model of Dynamic pedestrian-Agents)
¡ Learn agents by EM algorithm
14
start
goal
goal
start D
D
[Zhou+, IJCV2015]
B
B
B
B
Agents have D and B respectively
• D (dynamics) : Linear dynamic system
• B (belief) : Gaussian distributions
(start, goal)

9. Dynamics and Beliefs
¡ belief parameter
15
! = ($, &, ', () : dynamics
* = (+,, Φ,, +., Φ.): belief
/
0
(!, *, 1) : Agent model
1 : Weights
!"
!#
missing missingobserved$%
$&
'%~)($%, Φ%)
'&~)($&, Φ&)
$%
$&
.
Kalman filter + Kalman smoother
¡ dynamics parameter
!"#$
%"
Observation !"~'(!"|%")
= ,(!"|%", .)
State
!"#$
%!"#$ + '
!"~) !" !"#$
= +(!"|%!"#$ + ., 0)
*( ⋯ *)
ervations
/ 0-
Figure 1. State space model of MDA [9]
the sequence of states x except xs and xe. Figure 1 shows the state
= {yk} MDA estimates M agents ⇥ = {(Dm, Bm, ⇡m)} by maximizing
ood;
L =
X
k
log p(yk
, xk
, zk
, tk
s , tk
e|⇥), (6)
Hereafter, x1:T denotes the sequence of states x except xs and xe. Figure 1 shows the
pace model of MDA.
.2 Learning
Given K trajectories Y = {yk} MDA estimates M agents ⇥ = {(Dm, Bm, ⇡m)} by maxim
he following log likelihood;
L =
X
k
log p(yk
, xk
, zk
, tk
s , tk
e |⇥),
where the joint probability is given by
p(yk
, xk
, zk
, tk
s , tk
e ) = p(zk
)p(tk
s )p(tk
e )p(xk
s )p(xk
e )
⌧k
+tk
eY
t= tk
s +1
p(xk
t |xk
t 1)
⌧k
Y
t=1
p(yk
t |xk
t )
with respect to parameters ⇥.
This can be rewritten by replacing hidden variables H = {hk}, hk = {zk, tk
s , tk
e } as follow
¡ Joint distribution of trajectory k
¡ Log likelihood for k trajectories
3.2 Learning
Given K trajectories Y = {yk} MDA estimates M agents ⇥ = {(Dm, Bm, ⇡m)} by ma
the following log likelihood;
L =
X
k
log p(yk
, xk
, zk
, tk
s , tk
e |⇥),
where the joint probability is given by
p(yk
, xk
, zk
, tk
s , tk
e ) = p(zk
)p(tk
s )p(tk
e )p(xk
s )p(xk
e )
⌧k
+tk
eY
t= tk
s +1
p(xk
t |xk
t 1)
⌧k
Y
t=1
p(yk
t |xk
t )
with respect to parameters ⇥.
This can be rewritten by replacing hidden variables H = {hk}, hk = {zk, tk
s , tk
e } as fo
L =
X
k
log p(yk
, xk
, hk
|⇥)
Hereafter, x1:T denotes the sequence of states x except xs and xe. Figure 1 shows
space model of MDA.
3.2 Learning
Given K trajectories Y = {yk} MDA estimates M agents ⇥ = {(Dm, Bm, ⇡m)} by ma
the following log likelihood;
L =
X
k
log p(yk
, xk
, zk
, tk
s , tk
e |⇥),
where the joint probability is given by
p(yk
, xk
, zk
, tk
s , tk
e ) = p(zk
)p(tk
s )p(tk
e )p(xk
s )p(xk
e )
⌧k
+tk
eY
t= tk
s +1
p(xk
t |xk
t 1)
⌧k
Y
t=1
p(yk
t |xk
t )
with respect to parameters ⇥.
This can be rewritten by replacing hidden variables H = {hk}, hk = {zk, tk
s , tk
e } as fo
Hidden variables

10. Grahicsl model of MDA 16
D B
z
"# = "%&'
"( ")
*( ⋯
⋯⋯
*)
"%&',( "),(
⋯
"- = "),&.
Agents
States
Observations
/0# 0-
1
2
k
s e
ere the joint probability is given by
p(yk
, xk
, zk
, tk
s , tk
e ) = p(zk
)p(tk
s )p(tk
e )p(xk
s )p(xk
e )
⌧k
+tk
eY
t= tk
s +1
p(xk
t |xk
t 1)
⌧k
Y
t=1
p(yk
t |xk
t )
th respect to parameters ⇥.
This can be rewritten by replacing hidden variables H = {hk}, hk = {zk, tk
s , tk
e } as follows
L =
X
k
log p(yk
, xk
, hk
|⇥)
e EM algorithm estimates iteratively as H is not observed.
3

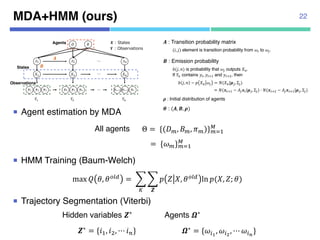
11. EM algorithm for MDA 17
¡ EM algorithm
max $ = &
'
log +(-'|/', ℎ', 2)
ℎ' = {5', 67
', 68
'}
:2∗ = arg =>?@A 2, :2
¡ E step
¡ M step
3.2.1 E step of original MDA
Q(⇥, ˆ⇥) = EX,H|Y,ˆ⇥[L]
= EH|Y,ˆ⇥[EX|Y,H,ˆ⇥[L]]
=
X
k
X
hk
k
Exk|yk,hk [log p(yk
, xk
, hk
|⇥)]
=
X
k
X
hk
k
log p(yk
, ˆxk
, hk
|⇥),
where ˆxk
= Exk|yk,hk [xk] is computed by the modified Kalman filter [9, 12
Weights k are posterior probabilities given as follows;
k
= p(hk
|yk
, ˆ⇥)
=
p(hk|ˆ⇥)p(yk|hk, ˆ⇥)
p(yk|ˆ⇥)
By further assuming the independence among hidden variables z, t , t , w
Q(⇥, ˆ⇥) = EX,H|Y,ˆ⇥[L]
= EH|Y,ˆ⇥[EX|Y,H,ˆ⇥[L]]
=
X
k
X
hk
k
Exk|yk,hk [log p(yk
, xk
, hk
|⇥)]
=
X
k
X
hk
k
log p(yk
, ˆxk
, hk
|⇥),
where ˆxk
= Exk|yk,hk [xk] is computed by the modified Kalman filter [9, 12].
Weights k are posterior probabilities given as follows;
k
= p(hk
|yk
, ˆ⇥)
=
p(hk|ˆ⇥)p(yk|hk, ˆ⇥)
p(yk|ˆ⇥)
By further assuming the independence among hidden variables z, ts, te, we have
p(hk
|ˆ⇥) = p(zk
, tk
s , tk
e|ˆ⇥) = p(zk
|ˆ⇥)p(tk
s |ˆ⇥)p(tk
e|ˆ⇥)
=
X
k
X
hk
k
log p(yk
, ˆxk
, hk
|⇥),
where ˆxk
= Exk|yk,hk [xk] is computed by the modified Kalman filter [9, 12].
Weights k are posterior probabilities given as follows;
k
= p(hk
|yk
, ˆ⇥)
=
p(hk|ˆ⇥)p(yk|hk, ˆ⇥)
p(yk|ˆ⇥)
By further assuming the independence among hidden variables z, ts, te, we have
p(hk
|ˆ⇥) = p(zk
, tk
s , tk
e |ˆ⇥) = p(zk
|ˆ⇥)p(tk
s |ˆ⇥)p(tk
e |ˆ⇥)
By removing ts, te by assuming those be uniform, we have
k
=
p(zk|ˆ⇥)p(yk|hk, ˆ⇥)
P
hk p(zk|ˆ⇥)p(yk|hk, ˆ⇥)
where likelihood p(yk|hk, ˆ⇥) is also computed by the modified Kalman filter [9, 12].
Kalman filter
3.2.1 E step of original M
Q(⇥
where ˆxk
= Exk|yk,hk [xk] i
Weights k are posterior
Weights

12. Issue of MDA 19
¡ One trajectory is represented by one agent model
¡ Cannot switch agent models in one trajectory
[Zhou+, IJCV2015]
D B
z
"# = "%&'
"( ")
*( ⋯
⋯⋯
*)
"%&',( "),(
⋯
"- = "),&.
Agents
States
Observations
/0# 0-
1
2

13. Related model : Switching Kalman Filter
¡ Can estimate agents !" in time series
¡ Transition probabilities between agent models are required
20
Observations
States
Agents z" z#$"z% z# z#&"⋯ ⋯
(" (#$"(% (# (#&"
)" )#$")% )# )#&"
⋯ ⋯
[Murphy, 1998]

14. MDA+HMM (ours)
¡ Each states belong to one agent model
¡ Regard three observations as one observation
¡ Learn transition probabilities ! between and emission probabilities "
of agents from trajectories
21
!" !# !$ !% !& !' !()# !()" !(⋯
+" +# +,
-" -# -,⋯
. /Agents
Observations
0" 0# 0,⋯
States
1
2
3
4

15. MDA+HMM (ours) 22
¡ Agent estimation by MDA
All agents Θ = {(%&, (&, )&)}&,-
.
= {/&}&,-
.
¡ HMM Training (Baum-Welch)
¡ Trajectory Segmentation (Viterbi)
0∗ = {2-, 23, ⋯ 25}
Hidden variables 0∗
6∗ = {/78
, /79
, ⋯ /7:
}
Agents 6∗
max > ?, ?@AB = C
D
C
0
E F G, ?@AB ln E(G, F; ?)
!" !# !$ !% !& !' !()# !()" !(⋯
+" +# +,
-" -# -,⋯
. /Agents
Observations
0" 0# 0,⋯
States
1
2
3
4
K : Emission probability
L : Initial distribution of agents
M : Transition probability matrix
N : (M, K, L)
(2, O) element is transition probability from /7 to /P.
Q(O, R) is probability that /P outputs G5.
If S5 contains TU, TUV- and TUV3, then
Q O, R ~ E G5 /P = X(G5|ZP, ΣP)
= X(UV- − ^PU|ZP, ΣP) _ X(UV3 − ^PUV-|ZP, ΣP)

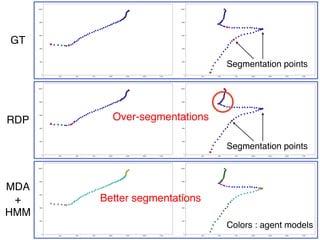
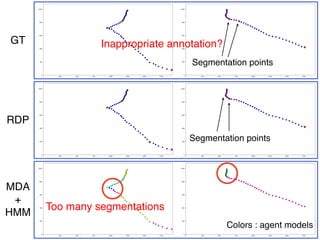
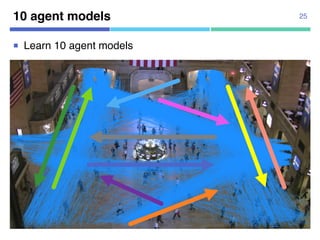
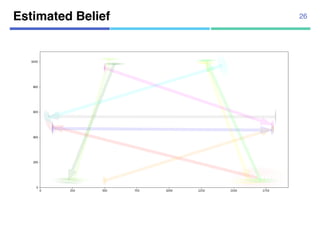
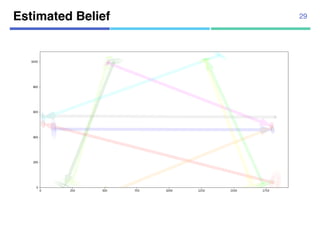
16. ¡ Real data
¡ 104 trajectories from “Pedestrian
Walking Path Dataset”
¡ Annotated segmentation points
manually
¡ 1920x1080 pixels
¡ 4-fold cross validation
Datasets
¡ Synthetic data
¡ Using 10 agent models
¡ Uniform transition probabilities
¡ 10,000 trajectories for estimation,
10,000 trajectories for test
¡ 1920x1080 pixels
23
[Yi+, CVPR2015]

17. ¡ Input trajectories
10 agent models 24

18. ¡ Learn 10 agent models
10 agent models 25

19. Estimated Belief 26

20. Estimated Belief 27

21. Estimated Belief 28

22. Estimated Belief 29

23. Visualizing MDA clustering and dynamics 30

24. Visualizing MDA clustering and dynamics 31

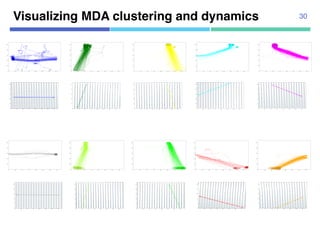
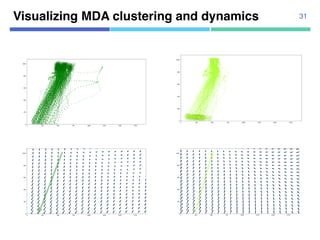
25. ¡ Real data
¡ 104 trajectories from “Pedestrian
Walking Path Dataset”
¡ Annotated segmentation points
manually
¡ 1920x1080 pixels
¡ 4-fold cross validation
Datasets
¡ Synthetic data
¡ Using 10 agent models
¡ Uniform transition probabilities
¡ 10,000 trajectories for estimation,
10,000 trajectories for test
¡ 1920x1080 pixels
32
[Yi+, CVPR2015]

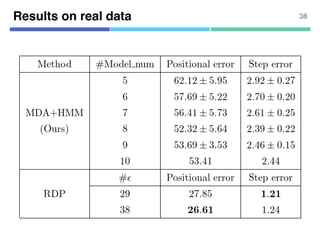
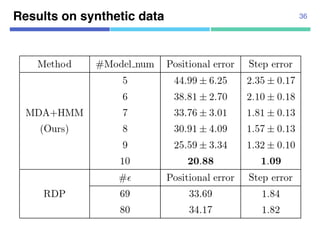
26. Baseline 33
¡ Ramer-Douglas-Peucker (RDP) algorithm
¡ Trajectory simplification with parameter !
¡ Segmentation with keeping trajectory’s shape
¡ Appropriate ! setting is required
¡ No estimation of agent models
Wikipedia, “Ramer–Douglas–Peucker algorithm”
[Ramer, 1972] [Douglas+, 1973]

27. Evaluation metrics
¡ Groundtruth
34
¡ Estimation
⋰
⋰
⋰
⋰
"" − 1
Positional error : Sum of L2 norm between Goundtruth and Estimation
Step error : Sum of absolute values of difference between Groundtruth and
Estimation are observed
: Segmentation points
Positional error
Step error

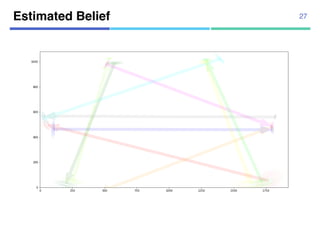
28. ¡ Real data
¡ 104 trajectories from “Pedestrian
Walking Path Dataset”
¡ Annotated segmentation points
manually
¡ 1920x1080 pixels
¡ 4-fold cross validation
Datasets
¡ Synthetic data
¡ Using 10 agent models
¡ Uniform transition probabilities
¡ 10,000 trajectories for estimation,
10,000 trajectories for test
¡ 1920x1080 pixels
35
[Yi+, CVPR2015]

29. Results on synthetic data 36

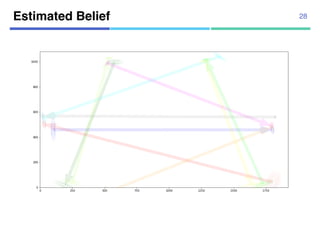
30. ¡ Real data
¡ 104 trajectories from “Pedestrian
Walking Path Dataset”
¡ Annotated segmentation points
manually
¡ 1920x1080 pixels
¡ 4-fold cross validation
Datasets
¡ Synthetic data
¡ Using 10 agent models
¡ Uniform transition probabilities
¡ 10,000 trajectories for estimation,
10,000 trajectories for test
¡ 1920x1080 pixels
37
[Yi+, CVPR2015]

31. Results on real data 38

32. 39
GT
RDP
MDA
+
HMM
Colors : agent models
Better segmentations
Over-segmentations
Segmentation points
Segmentation points

33. 40
GT
RDP
MDA
+
HMM
Too many segmentations
Inappropriate annotation?
Colors : agent models
Segmentation points
Segmentation points

34. 41

35. Conclusion 42
¡ We proposed semantic segmentation method (MDA+HMM)
by extending classification method (MDA)
¡ We validated effectiveness of proposed method by
comparing with baseline method (RDP) on synthetic and
real data
¡ We realized trajectory semantic segmentation based on
human behavior models