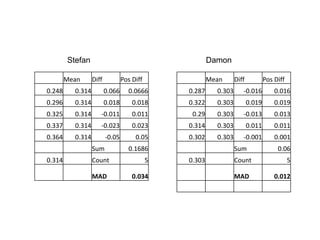
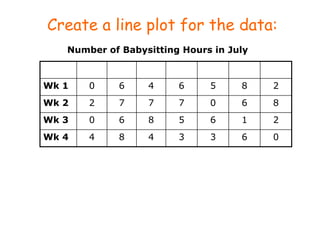
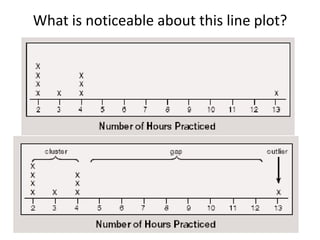
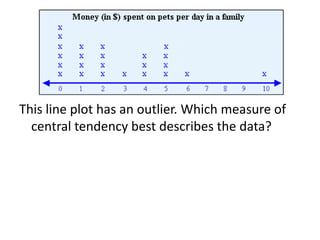
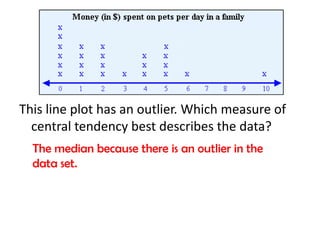
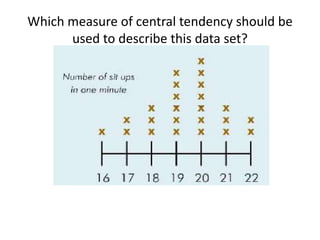
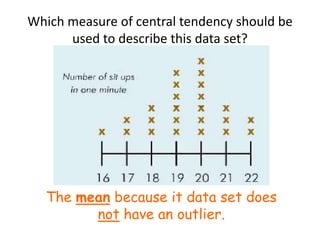
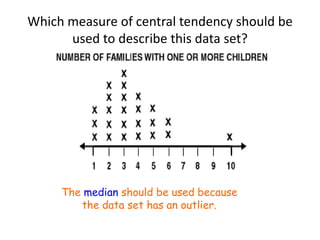
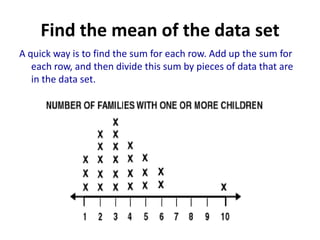
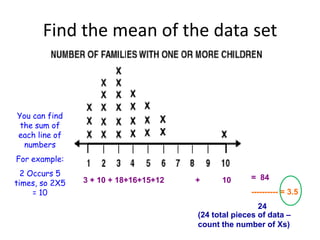
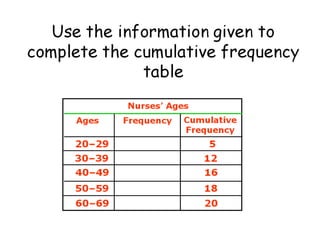
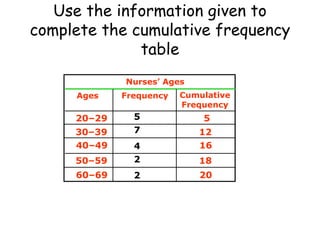
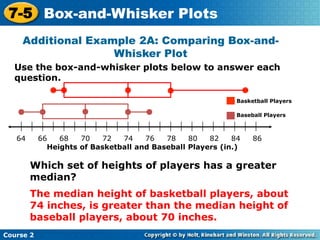
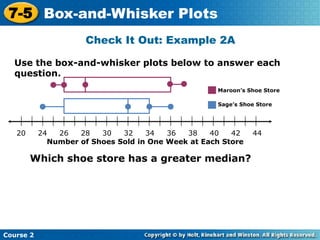
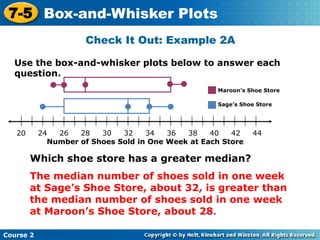
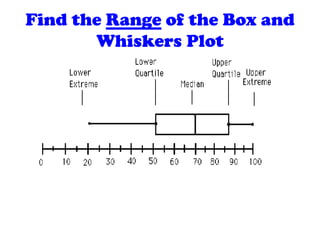
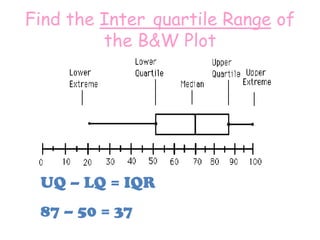
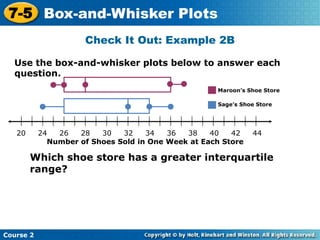
Here are the steps to find the mean of the data set: 1) List the data: 4, 6, 8, 10, 12 2) Find the sum of the data: 4 + 6 + 8 + 10 + 12 = 40 3) Count the number of data points: There are 5 data points 4) Divide the sum by the count: 40/5 = 8 Therefore, the mean of the data set is 8.

1. Unit 4 Midterm
Review

2. What is central tendency?

3. What is central tendency?
• It refers to the middle or center of the data.

4. What is the mean of a data set?

5. What is mean?
• It is called the average.
• You add up all the numbers to find a sum.
• You divide the sum by the total numbers in
the data set.

6. What is the median? How do you
find it?

7. What is the median? How do you find
it?
• It is the middle of the data.
• You put the numbers in order and eliminate
one on each side of the data until you find the
middle.

8. How do you find the median of a data set if
there are more than one number in the
middle of the data set?
2 5 6 12 15 18

9. How do you find the median of a data
set if there are more than one number
in the middle of the data set?
2 5 6 12 15 18
Find the mean of those two numbers by adding them up
and dividing by two.
6 + 12 = 18
18/2 = 9
The median would be 9

10. 1. Define mode.
2. What would it be for the
following data set?
• 1,2,2,2,3,5,6,7

11. Define mode. What would it be for
the following data set?
• The number that occurs most often in a data set.
• 1,2,2,2,3,5,6,7
• The mode would be 2, because it occurs the most often.
• Some data sets don’t have a more, while some may have
more than one.

12. Which measure of center is
affected by outliers?
• Hint: If you made a really low grade, what is
going to affected the most? (Mean or Median)

13. Which measure of central tendency is
affected by outliers?
Hint: If you made a really low grade, what is
going to affected the most? (Mean or Median)
The mean is affected by outliers. The mean of
the test scores will go down.
The median is not affected by outliers?

14. 1. Which set of data would have a higher
mean (average)?
2. Which set of data would have a higher
median?
3. Which data set had an outlier?
Data set 1: 5 5 15 20 25
Data set 2: 5 5 15 20 60

15. • 1. Which set of data would have a higher
mean (average)? - Data set 2
2. Which set of data would have a higher
median? – They both have the same median
3. Which data set had an outlier? – Data set 2

16. What affect will an extremely small
outlier have on a set of data?
Hint: For example, if you have a really low test grade, how will
this affect the mean and median for the set of data?

17. What affect will an extremely small
outlier have on a set of data?
Hint: For example, if you have a really low test grade, how will
this affect the mean and median for the set of data?
The small outlier will bring down the
mean (average).
The median will not really be affected.

18. How will really large outliers affect the
mean and median of a set of data?

19. How will really large outliers affect the
mean and median of a set of data?
• The large outlier will cause the mean
(average) to increase.
• It will not really affect the median.

20. Before
• We measured the
heights of the
cans and created
data sets.
• What happens to
the measures of
center after we After
replace the
tallest can with
the Pringles can?

21. Before
• We measured the
heights of the
cans and created
data sets.
• What happens to
the measures of
center after we After
replace the
tallest can with
the Pringles can?
• The mean increased.
• The median stayed the
same.

22. Can you name a real example of how
mode is used in the real world?

23. Can you name a real example of how
mode is used in the real world?
• Voting - the candidate with the most
votes, wins.

24. Find the Mean Absolute Deviation
(MAD) for both people. Find who is
more consistent hitter.
Batting Averages:
Stefan: .248, .296, .325, .337, .364
Damon: .287. .322, .290, .314, .302
Be sure to make a table for each baseball player.

25. Stefan Damon
Mean Diff Pos Diff Mean Diff Pos Diff
0.248 0.314 0.066 0.0666 0.287 0.303 -0.016 0.016
0.296 0.314 0.018 0.018 0.322 0.303 0.019 0.019
0.325 0.314 -0.011 0.011 0.29 0.303 -0.013 0.013
0.337 0.314 -0.023 0.023 0.314 0.303 0.011 0.011
0.364 0.314 -0.05 0.05 0.302 0.303 -0.001 0.001
Sum 0.1686 Sum 0.06
0.314 Count 5 0.303 Count 5
MAD 0.034 MAD 0.012

26. Complete the Frequency column in this cumulative
frequency table
The list shows the average high temperatures for 20 cities
on one February day.
69, 66, 65, 51, 50, 50, 44, 41, 38, 32, 32, 28, 20, 18, 12, 8,
8, 4, 2, 2
February Temperatures in 20 Cities
Hint: Count the Average Frequency Cumulative
Highs Frequency
numbers that fall
into each interval 0–19
category, and 20–39
place that total 40–59
under frequency.
60–79

27. Complete the Cumulative Frequency
column
The list shows the average high temperatures for 20 cities
on one February day. Make a cumulative frequency table of
the data.
February Temperatures in 20 Cities
Average Frequency Cumulative
Step 3: Find the Highs Frequency
cumulative frequency 0–19 7 7
for each row by adding
all the frequency values 20–39 5 12
that are above or in 40–59 5 17
that row.
60–79 3 20

28. A stem-and-leaf plot can be used to show how often data
values occur and how they are distributed.
Each leaf on the plot represents the right-hand digit in a
data value.
Stems represents left-hand digits.
Stems Leaves
2 4 7 9
3 0 6
Key: 2|7 means 27

29. Create a stem and leaf plot
The data shows the number of years coached by the top
15 coaches in the all-time NFL coaching victories. Make
a stem-and-leaf plot of the data.
33, 40, 29, 33, 23, 22, 20, 21, 18, 23, 17, 15, 15, 12, 17
Step 2: List the stems from least to greatest on the plot.
The stems
are the tens
Stems Leaves
digits.
1
2
3
4

30. Creating Stem and Leaf Plot
The data shows the number of years coached by the top 15 coaches in the all-
time NFL coaching victories. Make a stem-and-leaf plot of the data. Then find
the number of coaches who coached fewer than 25 years.
33, 40, 29, 33, 23, 22, 20, 21, 18, 23, 17, 15, 15, 12, 17
Step 3: List the leaves for each stem from least to greatest.
The stems The leaves
are the tens are the
Stems Leaves
digits. ones digits.
1 2 5 5 7 7 8
2 0 1 23 3 9
3 3 3
4 0

31. Would it be appropriate to make a
stem and leaf plot for the number of
text message you send Monday
through Friday?

32. Would it be appropriate to make a
stem and leaf plot for the number of
text message you send Monday
through Friday?
• No because you would be examining two
variables ( number of messages, and days of
the week).
• Stem and leaf plots are only appropriate when
you are examining one variable, such as the
number of text message, or test grades in
math.

33. Create a line plot for the data:
Number of Babysitting Hours in July
M T W Th F S Su
Wk 1 0 6 4 6 5 8 2
Wk 2 2 7 7 7 0 6 8
Wk 3 0 6 8 5 6 1 2
Wk 4 4 8 4 3 3 6 0

34. Your line plot should look like this:
Step 2: Put an X above the number on the number
line that corresponds to the number of babysitting
hours in July. X
X
X X X
X X X X X X
X X X X X X X X
X X X X X X X X X
0 1 2 3 4 5 6 7 8
The greatest number of X’s appear above the number 6.
This means that Morgan babysat most often for 6 hours.

35. Find the median of the line plot
that you just created.

37. What is noticeable about this line plot?

38. What is noticeable about this line plot?

39. This line plot has an outlier. Which measure of
central tendency best describes the data?

40. This line plot has an outlier. Which measure of
central tendency best describes the data?
The median because there is an outlier in the
data set.

41. Which measure of central tendency should be
used to describe this data set?

42. Which measure of central tendency should be
used to describe this data set?
The mean because it data set does
not have an outlier.

43. Which measure of central tendency should be
used to describe this data set?

44. Which measure of central tendency should be
used to describe this data set?
The median should be used because
the data set has an outlier.

45. Find the mean of the data set
A quick way is to find the sum for each row. Add up the sum for
each row, and then divide this sum by pieces of data that are
in the data set.

46. Find the mean of the data set
You can find
the sum of
each line of
numbers
For example:
2 Occurs 5 = 84
times, so 2X5 3 + 10 + 18+16+15+12 + 10
= 10 ---------- = 3.5
24
(24 total pieces of data –
count the number of Xs)

48. Use the information given to
complete the cumulative frequency
table
Nurses’ Ages
Ages Frequency Cumulative
Frequency
20–29 5 5
30–39 7 12
40–49 4 16
50–59 2 18
60–69 2 20

49. What is a population?

50. Population
= the entire group
• Researchers often study
a part of the population,
called a sample.

51. What is a sample?

52. Sample is a small group
of the total population

53. What is a random sample?

54. •For a random sample,
members of the population are
chosen at random. This gives
every member of the
population an equal chance of
being chosen.

55. What is a convenience sample?

56. CONVENIENCE SAMPLE
• A convenience sample is based
on members of the population
that are conveniently available,
such as 30 elk in a wildlife
preservation area.

57. •A biased sample does not
fairly represent the
population.
• A study of 50 elk belonging to a breeder
could be biased because the breeder’s elk
might be less likely to have Mad Elk
Disease than elk in the wild.

58. Which would be better to have, a
random sample or a convenience
sample?

59. Which would be better to have, a
random sample or a convenience
sample?
A random sample is more likely
to be representative of a
population than a convenience
sample is.

61. Min - 22
LQ - 24
Med - 31
UQ - 38
Max - 42

62. Box-and-Whisker Plots
Data from the previous question
(min, LQ, med, UQ, max)
42 22 31 27 24 38 35
Step 1: Order the data from least to greatest. Then find the
least and greatest values, the median, and the lower
and upper quartiles.
The least value.
22 24 27 31 35 38 42
The greatest value.
22 24 27 31 35 38 42 The median.
The upper and lower
22 24 27 31 35 38 42
quartiles.
Course 2

63. Create a box and whiskers from
the 5 number summary you just
found.

64. 7-5 Box-and-Whisker Plots
Above the number line, plot a point for each
value in Step 1.
Step 3: Draw a box from the lower to the upper quartile.
Inside the box, draw a vertical line through the median.
Then draw the “whiskers” from the box to the least
and greatest values.
20 22 24 26 28 30 32 34 36 38 40 42
Course 2

65. 7-5 Box-and-Whisker Plots
Additional Example 2A: Comparing Box-and-
Whisker Plot
Use the box-and-whisker plots below to answer each
question.
Basketball Players
Baseball Players
64 66 68 70 72 74 76 78 80 82 84 86
t Heights of Basketball and Baseball Players (in.)
Which set of heights of players has a greater
median?
Course 2

66. 7-5 Box-and-Whisker Plots
Additional Example 2A: Comparing Box-and-
Whisker Plot
Use the box-and-whisker plots below to answer each
question.
Basketball Players
Baseball Players
64 66 68 70 72 74 76 78 80 82 84 86
t Heights of Basketball and Baseball Players (in.)
Which set of heights of players has a greater
median?
The median height of basketball players, about
74 inches, is greater than the median height of
baseball players, about 70 inches.
Course 2

67. 7-5 Box-and-Whisker Plots
Check It Out: Example 2A
Use the box-and-whisker plots below to answer each
question.
Maroon’s Shoe Store
Sage’s Shoe Store
20 24 26 28 30 32 34 36 38 40 42 44
t Number of Shoes Sold in One Week at Each Store
Which shoe store has a greater median?
Course 2

68. 7-5 Box-and-Whisker Plots
Check It Out: Example 2A
Use the box-and-whisker plots below to answer each
question.
Maroon’s Shoe Store
Sage’s Shoe Store
20 24 26 28 30 32 34 36 38 40 42 44
t Number of Shoes Sold in One Week at Each Store
Which shoe store has a greater median?
The median number of shoes sold in one week
at Sage’s Shoe Store, about 32, is greater than
the median number of shoes sold in one week
at Maroon’s Shoe Store, about 28.
Course 2

69. Find the Range of the Box and
Whiskers Plot

70. Find the Range of the Box and
Whiskers Plot
Max – min = range
100 – 20 = 80

71. Find the Inter quartile Range of
the B&W Plot

72. Find the Inter quartile Range of
the B&W Plot
UQ – LQ = IQR
87 – 50 = 37

73. What is the range of the box known
as?

74. What is the range of the box known
as?
• Interquartile range

75. 7-5 Box-and-Whisker Plots
Check It Out: Example 2B
Use the box-and-whisker plots below to answer each
question.
Maroon’s Shoe Store
Sage’s Shoe Store
20 24 26 28 30 32 34 36 38 40 42 44
t Number of Shoes Sold in One Week at Each Store
Which shoe store has a greater interquartile
range?
Course 2

76. 7-5 Box-and-Whisker Plots
Check It Out: Example 2B
Use the box-and-whisker plots below to answer each
question.
Maroon’s Shoe Store
Sage’s Shoe Store
20 24 26 28 30 32 34 36 38 40 42 44
t Number of Shoes Sold in One Week at Each Store
Which shoe store has a greater interquartile
range?
Maroon’s shoe store has a longer box, so it has
a greater interquartile range.
Course 2

77. I would like to create a graph to show
the number of cancer cases world
wide from 1950 to 2011. What kind of
graph would be best?

78. I would like to create a graph to show
the number of cancer cases world
wide from 1950 to 2011. What kind of
graph would be best?
• Line graph because it shows change over time

79. What kind of graphs should I use if
percents or populations are involved?

80. What kind of graphs should I use if
percents or populations are involved?
• Circle graph

81. If I want to create a display to show the
number of cell phone messages sent from
Monday – Friday, what kind of graph would
be best?

82. If I want to create a display to show the
number of cell phone messages sent from
Monday – Friday, what kind of graph would
be best?
• Line Graph – it shows change over time

83. If I wanted to create a display to show test
scores in math, SS, science, and LA, what kind
of graph would be best?

84. If I wanted to create a display to show test
scores in math, SS, science, and LA, what kind
of graph would be best?
• Bar Graph – each set of data (subject) is not
related to the other

85. I want to create a display to show the
classes grade on the final exam. What
kind of graphs would be the best?

86. I want to create a display to show the
classes grade on the final exam. What
kind of graphs would be the best?
• Stem and Leaf
• Line Plot
• or histogram