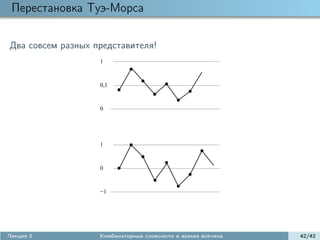
Документ представляет собой лекцию об комбинаторных сложностях бесконечных слов, рассматривающую определения, свойства и сложности различных типов бесконечных слов. Основное внимание уделяется функциям сложности, периодическим и непериодическим словам, а также значениям арифметической сложности, включая теоремы о линейной сложности. Приведены примеры и вопросы о сложности слов туэ-морса, дракона и штурма.

1. Комбинаторные сложностные характеристики
бесконечных слов
Анна (Эдуардовна) Фрид
ИМ им. С. Л. Соболева СО РАН, Новосибирск
anna.e.frid@gmail.com
Лекция 5, 16.10.2011
Лекция 5 Комбинаторные сложности и всякая всячина 1/42

2. Комбинаторная сложность
Определение
Комбинаторной сложностью бесконечного слова w называется
функция pw (n), равная числу его подслов длины n.
Лекция 5 Комбинаторные сложности и всякая всячина 2/42

3. Комбинаторная сложность
Определение
Комбинаторной сложностью бесконечного слова w называется
функция pw (n), равная числу его подслов длины n.
Example
В слове Туэ-Морса
0110 1001 1001 0110 1001 0110 0110 1001 · · ·
не встречаются слова 000 и 111, поэтому pTM (3) = 6.
Лекция 5 Комбинаторные сложности и всякая всячина 2/42

4. Свойства функции сложности
Напомним, что слово (со временем) периодическое, если имеет вид
uvvvvvv · · · .
Лекция 5 Комбинаторные сложности и всякая всячина 3/42

5. Свойства функции сложности
Напомним, что слово (со временем) периодическое, если имеет вид
uvvvvvv · · · .
Для любого бесконечного слова над алфавитом мощности q
1 ≤ pw (n) ≤ q n ;
Лекция 5 Комбинаторные сложности и всякая всячина 3/42

6. Свойства функции сложности
Напомним, что слово (со временем) периодическое, если имеет вид
uvvvvvv · · · .
Для любого бесконечного слова над алфавитом мощности q
1 ≤ pw (n) ≤ q n ;
Функция pw (n) не убывает;
Лекция 5 Комбинаторные сложности и всякая всячина 3/42

7. Свойства функции сложности
Напомним, что слово (со временем) периодическое, если имеет вид
uvvvvvv · · · .
Для любого бесконечного слова над алфавитом мощности q
1 ≤ pw (n) ≤ q n ;
Функция pw (n) не убывает;
Функция pw (n) ограничена тогда и только тогда, когда слово w со
временем периодично.
Лекция 5 Комбинаторные сложности и всякая всячина 3/42

8. Свойства функции сложности (продолжение)
Минимальная сложность непериодических слов равна n + 1 (слова
Штурма).
Лекция 5 Комбинаторные сложности и всякая всячина 4/42

9. Свойства функции сложности (продолжение)
Минимальная сложность непериодических слов равна n + 1 (слова
Штурма).
Сложность автоматных слов растет линейно.
Лекция 5 Комбинаторные сложности и всякая всячина 4/42

10. Свойства функции сложности (продолжение)
Минимальная сложность непериодических слов равна n + 1 (слова
Штурма).
Сложность автоматных слов растет линейно.
Сложность неподвижных точек морфизмов растет как O(n2 ),
O(n log n), O(n log log n), O(n) или O(1) [Pansiot 1984].
Лекция 5 Комбинаторные сложности и всякая всячина 4/42

11. Свойства функции сложности (продолжение)
Минимальная сложность непериодических слов равна n + 1 (слова
Штурма).
Сложность автоматных слов растет линейно.
Сложность неподвижных точек морфизмов растет как O(n2 ),
O(n log n), O(n log log n), O(n) или O(1) [Pansiot 1984].
Сложность морфических слов растет как O(n1+1/k ) для
некоторого k или как O(n log n) (или медленнее) [Devyatov, 2008:
доказательство опубликовано частично].
Лекция 5 Комбинаторные сложности и всякая всячина 4/42

12. Свойства функции сложности (продолжение)
Минимальная сложность непериодических слов равна n + 1 (слова
Штурма).
Сложность автоматных слов растет линейно.
Сложность неподвижных точек морфизмов растет как O(n2 ),
O(n log n), O(n log log n), O(n) или O(1) [Pansiot 1984].
Сложность морфических слов растет как O(n1+1/k ) для
некоторого k или как O(n log n) (или медленнее) [Devyatov, 2008:
доказательство опубликовано частично].
Если сложность слова растет линейно, то ее первые разности
ограничены [Cassaigne, 1996].
Лекция 5 Комбинаторные сложности и всякая всячина 4/42

13. Метод специальных слов
Рассмотрим продолжаемый факторный язык F например, язык
подслов бесконечного слова.
Продолжаемый: ∀u ∈ F ∃a, b ∈ Σ : aub ∈ F .
Факторный: замкнутый относительно взятия подслова.
Лекция 5 Комбинаторные сложности и всякая всячина 5/42

14. Метод специальных слов
Рассмотрим продолжаемый факторный язык F например, язык
подслов бесконечного слова.
Продолжаемый: ∀u ∈ F ∃a, b ∈ Σ : aub ∈ F .
Факторный: замкнутый относительно взятия подслова.
Обозначим через l(u) (r (u)) множество символов, которыми слово u
может быть продолжено влево (вправо), и назовем специальным влево
(вправо) слово, у которого l(u) = 1 (r (u) = 1).
Лекция 5 Комбинаторные сложности и всякая всячина 5/42

15. Метод специальных слов
Обозначим через F (n) множество всех слов языка F длины n, а через
L(n) множество его специальных слов длины n.
Лекция 5 Комбинаторные сложности и всякая всячина 6/42

16. Метод специальных слов
Обозначим через F (n) множество всех слов языка F длины n, а через
L(n) множество его специальных слов длины n.
Тогда первые разности комбинаторной сложности:
p (n) = p(n + 1) − p(n) = (l(u) − 1) = (l(u) − 1).
u∈F (n) u∈L(n)
p (n) = p(n + 1) − p(n) = (r (u) − 1) = (r (u) − 1).
u∈F (n) u∈R(n)
Лекция 5 Комбинаторные сложности и всякая всячина 6/42

17. Биспециальные слова
Слово биспециально, если оно специально справа и слева. Множество
B(n).
Лекция 5 Комбинаторные сложности и всякая всячина 7/42

18. Биспециальные слова
Слово биспециально, если оно специально справа и слева. Множество
B(n).
Степень биспециальности:
b(v ) = #{(a, b)|a, b ∈ Σ, avb ∈ F } − l(v ) − r (v ) + 1
Лекция 5 Комбинаторные сложности и всякая всячина 7/42

19. Биспециальные слова
Слово биспециально, если оно специально справа и слева. Множество
B(n).
Степень биспециальности:
b(v ) = #{(a, b)|a, b ∈ Σ, avb ∈ F } − l(v ) − r (v ) + 1
p(n + 2) − 2p(n + 1) + p(n) = p (n) = b(v ) = b(v ).
v ∈F (n) v ∈B(n)
Лекция 5 Комбинаторные сложности и всякая всячина 7/42

20. Граф биспециальности
1 1
2 2
L(v) R(v)
l(v)
r(v)
Лекция 5 Комбинаторные сложности и всякая всячина 8/42

21. Граф биспециальности
1 1
2 2
L(v) R(v)
l(v)
r(v)
История: Cassaigne 1994,1997; Августинович 1994 (Туэ-Морс),
Августинович-Фрид 1998.
Лекция 5 Комбинаторные сложности и всякая всячина 8/42

22. Линейная сложность
Характеризации бесконечных слов с линейной комбинаторной
сложностью нет.
S-adic conjecture
Бесконечное слово имеет линейную комбинаторную сложность тогда и
только тогда, когда каким-то образом задается морфизмами.
Лекция 5 Комбинаторные сложности и всякая всячина 9/42

23. Линейная сложность
Характеризации бесконечных слов с линейной комбинаторной
сложностью нет.
S-adic conjecture
Бесконечное слово имеет линейную комбинаторную сложность тогда и
только тогда, когда каким-то образом задается морфизмами.
S. Ferenczi продвинулся дальше всех
Лекция 5 Комбинаторные сложности и всякая всячина 9/42

24. Арифметическая сложность
Арифметическим замыканием бесконечного слова w = w0 w1 · · · wn · · ·
называется множество
Aw = {wk wk+d wk+2d · · · wk+(n−1)d |k ≥ 0, d > 0}.
Лекция 5 Комбинаторные сложности и всякая всячина 10/42

25. Арифметическая сложность
Арифметическим замыканием бесконечного слова w = w0 w1 · · · wn · · ·
называется множество
Aw = {wk wk+d wk+2d · · · wk+(n−1)d |k ≥ 0, d > 0}.
Арифметическая сложность aw (n) определяется как
aw (n) = #(Aw ∩ Σn ).
Avgustinovich, Fon-Der-Flaass, Frid 2000 (2003).
Лекция 5 Комбинаторные сложности и всякая всячина 10/42

26. Свойства арифметической сложности
Для любого бесконечного слова над алфавитом мощности q
pw (n) ≤ aw (n) ≤ q n ;
Лекция 5 Комбинаторные сложности и всякая всячина 11/42

27. Свойства арифметической сложности
Для любого бесконечного слова над алфавитом мощности q
pw (n) ≤ aw (n) ≤ q n ;
Функция aw (n) не убывает;
Лекция 5 Комбинаторные сложности и всякая всячина 11/42

28. Свойства арифметической сложности
Для любого бесконечного слова над алфавитом мощности q
pw (n) ≤ aw (n) ≤ q n ;
Функция aw (n) не убывает;
Функция aw (n) ограничена тогда и только тогда, когда слово w со
временем периодично.
Лекция 5 Комбинаторные сложности и всякая всячина 11/42

29. Свойства арифметической сложности
Для любого бесконечного слова над алфавитом мощности q
pw (n) ≤ aw (n) ≤ q n ;
Функция aw (n) не убывает;
Функция aw (n) ограничена тогда и только тогда, когда слово w со
временем периодично.
Theorem (Ван-дер-Варден)
∀w ∀n ∃a ∈ Σ | an ∈ Aw .
Лекция 5 Комбинаторные сложности и всякая всячина 11/42

30. Естественные вопросы
Какова арифметическая сложность слова Туэ-Морса?
Лекция 5 Комбинаторные сложности и всякая всячина 12/42

31. Естественные вопросы
Какова арифметическая сложность слова Туэ-Морса?
Слова дракона?
Лекция 5 Комбинаторные сложности и всякая всячина 12/42

32. Естественные вопросы
Какова арифметическая сложность слова Туэ-Морса?
Слова дракона?
Слов Штурма?
Лекция 5 Комбинаторные сложности и всякая всячина 12/42

33. Естественные вопросы
Какова арифметическая сложность слова Туэ-Морса?
Слова дракона?
Слов Штурма?
Когда сложность минимальна?
Лекция 5 Комбинаторные сложности и всякая всячина 12/42

34. Естественные вопросы
Какова арифметическая сложность слова Туэ-Морса?
Слова дракона?
Слов Штурма?
Когда сложность минимальна?
Когда сложность линейна?
Лекция 5 Комбинаторные сложности и всякая всячина 12/42

35. Естественные вопросы
Какова арифметическая сложность слова Туэ-Морса?
Слова дракона?
Слов Штурма?
Когда сложность минимальна?
Когда сложность линейна?
Какой она вообще может быть?
Лекция 5 Комбинаторные сложности и всякая всячина 12/42

36. Арифметическая сложность некоторых слов
Theorem (AFF)
Арифметическая сложность слова Туэ-Морса равна 2n .
Лекция 5 Комбинаторные сложности и всякая всячина 13/42

37. Арифметическая сложность некоторых слов
Theorem (AFF)
Арифметическая сложность слова Туэ-Морса равна 2n .
Доказательство: a, b ∈ ATM одинаковой длины =⇒ a ⊕ b ∈ ATM .
Лекция 5 Комбинаторные сложности и всякая всячина 13/42

38. Арифметическая сложность некоторых слов
Theorem (AFF)
Арифметическая сложность слова Туэ-Морса равна 2n .
Доказательство: a, b ∈ ATM одинаковой длины =⇒ a ⊕ b ∈ ATM .
Theorem (AFF)
Арифметическая сложность слова дракона равна 8n начиная с n = 14.
Лекция 5 Комбинаторные сложности и всякая всячина 13/42

39. Слово дракона (paperfolding word)
w = w1 w2 w3 · · · ∈ {1, −1}ω
P = 1 −1
w (0) =
w (1) = 1 -1 1 -1 1 -1 1 -1
w (2) = 1 1 -1 1 -1 -1 1 1 -1 1 -1 -1
w (3) = 1 1 -1 1 1 -1 -1 1 1 -1 -1 1 -1 -1
w = 1 1 -1 1 1 -1 -1 1 1 1 -1 -1 1 -1 -1
Это код кривой дракона: 1 налево, -1 направо (или наоборот).
Лекция 5 Комбинаторные сложности и всякая всячина 14/42

40. Арифметическая сложность слов Штурма
y
y=β x+γ
1−α
α
1 x
0 0 0 0 1 0 1
Это из предыдущей лекции: Cassaigne, F., 2007. O(n3 ).
Лекция 5 Комбинаторные сложности и всякая всячина 15/42

41. Минимальная арифметическая сложность
Avgustinovich, Cassaigne, Frid, 2006: минимальная арифметическая
сложность из равномерно рекуррентных слов у следующих слов
Т¨плица:
e
P0,k = 0 · · · 0
k
P1,k = 1 · · · 1
k
(Здесь k просто!)
k = 3:
w (0) =
w (1) = 0 0 0 0 0 0 0 -0 0 0
w (1) = 0 0 1 0 0 1 0 0 0 -0 1 0 0 1
w = 001001000 001001000 001001001 001001000 · · · = P0,3 ·P1,3 ·P0,3 · · · .
Лекция 5 Комбинаторные сложности и всякая всячина 16/42

42. Линейная арифметическая сложность
Theorem (Frid, 2005)
Арифметическая сложность равномерно рекуррентного слова линейна
тогда и только тогда, когда его множество подслов такое же, как у
слов Теплица, порожденных периодичной (возможно, с предпериодом)
последовательностью p-регулярных шаблонов Теплица, где p просто.
p-регулярный шаблон:
T = a1 a2 · · · ap−1 ap+1 · · · a2p−1 · · · a(k−1)p+1 · · · akp−1 .
Лекция 5 Комбинаторные сложности и всякая всячина 17/42

43. Промежуточная арифметическая сложность
Theorem (Salimov, 2009)
Существуют бесконечные слова с арифметической сложностью,
растущей быстрее, чем любой полином, но медленнее, чем αn для
любого α > 1.
Лекция 5 Комбинаторные сложности и всякая всячина 18/42

44. Промежуточная арифметическая сложность
Theorem (Salimov, 2009)
Существуют бесконечные слова с арифметической сложностью,
растущей быстрее, чем любой полином, но медленнее, чем αn для
любого α > 1.
Ср. с
Theorem (Cassaigne, 2002)
Существуют бесконечные слова с комбинаторной сложностью,
растущей быстрее, чем любой полином, но медленнее, чем αn для
любого α > 1.
Лекция 5 Комбинаторные сложности и всякая всячина 18/42

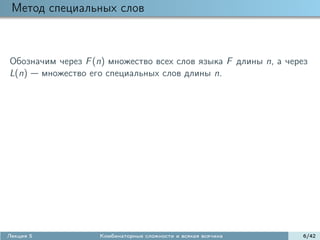
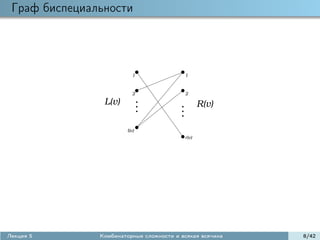
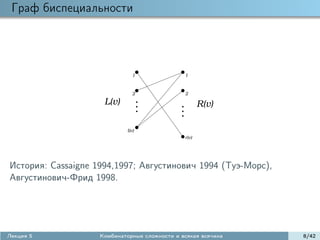
45. Сложность Камаэ
T = {0, m1 , . . . , mk−1 }: k-окно.
Для слова u = u0 u1 · · · un · · · :
un+T = un un+m1 · · · un+mk−1 T -подслово;
pu (T ) = {un+T |n = 0, 1, . . .} T -сложность слова u;
∗
max pu (T ) = pu (n) максимальная шаблонная сложность или
|T |=k
сложность Камаэ слова u.
[Kamae, Zamboni, 2002]
01001010100101 · · · T = (0, 2, 5)
Лекция 5 Комбинаторные сложности и всякая всячина 19/42

46. Сложность Камаэ
T = {0, m1 , . . . , mk−1 }: k-окно.
Для слова u = u0 u1 · · · un · · · :
un+T = un un+m1 · · · un+mk−1 T -подслово;
pu (T ) = {un+T |n = 0, 1, . . .} T -сложность слова u;
∗
max pu (T ) = pu (n) максимальная шаблонная сложность или
|T |=k
сложность Камаэ слова u.
[Kamae, Zamboni, 2002]
01001010100101 · · · T = (0, 2, 5)
Лекция 5 Комбинаторные сложности и всякая всячина 20/42

47. Сложность Камаэ
T = {0, m1 , . . . , mk−1 }: k-окно.
Для слова u = u0 u1 · · · un · · · :
un+T = un un+m1 · · · un+mk−1 T -подслово;
pu (T ) = {un+T |n = 0, 1, . . .} T -сложность слова u;
∗
max pu (T ) = pu (n) максимальная шаблонная сложность или
|T |=k
сложность Камаэ слова u.
[Kamae, Zamboni, 2002]
01001010100101 · · · T = (0, 2, 5)
Лекция 5 Комбинаторные сложности и всякая всячина 21/42

48. Сложность Камаэ
T = {0, m1 , . . . , mk−1 }: k-окно.
Для слова u = u0 u1 · · · un · · · :
un+T = un un+m1 · · · un+mk−1 T -подслово;
pu (T ) = {un+T |n = 0, 1, . . .} T -сложность слова u;
∗
max pu (T ) = pu (n) максимальная шаблонная сложность или
|T |=k
сложность Камаэ слова u.
[Kamae, Zamboni, 2002]
01001010100101 · · · T = (0, 2, 5)
Лекция 5 Комбинаторные сложности и всякая всячина 22/42

49. Сложность Камаэ
T = {0, m1 , . . . , mk−1 }: k-окно.
Для слова u = u0 u1 · · · un · · · :
un+T = un un+m1 · · · un+mk−1 T -подслово;
pu (T ) = {un+T |n = 0, 1, . . .} T -сложность слова u;
∗
max pu (T ) = pu (n) максимальная шаблонная сложность или
|T |=k
сложность Камаэ слова u.
[Kamae, Zamboni, 2002]
01001010100101 · · · T = (0, 2, 5)
Лекция 5 Комбинаторные сложности и всякая всячина 23/42

50. Сложность Камаэ
T = {0, m1 , . . . , mk−1 }: k-окно.
Для слова u = u0 u1 · · · un · · · :
un+T = un un+m1 · · · un+mk−1 T -подслово;
pu (T ) = {un+T |n = 0, 1, . . .} T -сложность слова u;
∗
max pu (T ) = pu (n) максимальная шаблонная сложность или
|T |=k
сложность Камаэ слова u.
[Kamae, Zamboni, 2002]
01001010100101 · · · T = (0, 2, 5)
Лекция 5 Комбинаторные сложности и всякая всячина 24/42

51. Сложность Камаэ
T = {0, m1 , . . . , mk−1 }: k-окно.
Для слова u = u0 u1 · · · un · · · :
un+T = un un+m1 · · · un+mk−1 T -подслово;
pu (T ) = {un+T |n = 0, 1, . . .} T -сложность слова u;
∗
max pu (T ) = pu (n) максимальная шаблонная сложность или
|T |=k
сложность Камаэ слова u.
[Kamae, Zamboni, 2002]
01001010100101 · · · T = (0, 2, 5)
Лекция 5 Комбинаторные сложности и всякая всячина 25/42

52. Сложность Камаэ
T = {0, m1 , . . . , mk−1 }: k-окно.
Для слова u = u0 u1 · · · un · · · :
un+T = un un+m1 · · · un+mk−1 T -подслово;
pu (T ) = {un+T |n = 0, 1, . . .} T -сложность слова u;
∗
max pu (T ) = pu (n) максимальная шаблонная сложность или
|T |=k
сложность Камаэ слова u.
[Kamae, Zamboni, 2002]
01001010100101 · · · T = (0, 2, 5)
Лекция 5 Комбинаторные сложности и всякая всячина 26/42

53. Сложность Камаэ
T = {0, m1 , . . . , mk−1 }: k-окно.
Для слова u = u0 u1 · · · un · · · :
un+T = un un+m1 · · · un+mk−1 T -подслово;
pu (T ) = {un+T |n = 0, 1, . . .} T -сложность слова u;
∗
max pu (T ) = pu (n) максимальная шаблонная сложность или
|T |=k
сложность Камаэ слова u.
[Kamae, Zamboni, 2002]
01001010100101 · · · T = (0, 2, 5)
Лекция 5 Комбинаторные сложности и всякая всячина 27/42

54. Сложность Камаэ
T = {0, m1 , . . . , mk−1 }: k-окно.
Для слова u = u0 u1 · · · un · · · :
un+T = un un+m1 · · · un+mk−1 T -подслово;
pu (T ) = {un+T |n = 0, 1, . . .} T -сложность слова u;
∗
max pu (T ) = pu (n) максимальная шаблонная сложность или
|T |=k
сложность Камаэ слова u.
[Kamae, Zamboni, 2002]
01001010100101 · · · T = (0, 2, 5)
Лекция 5 Комбинаторные сложности и всякая всячина 28/42

55. Низкая сложность Камаэ
Theorem (Kamae, Zamboni, 2002)
Бесконечное слово w не периодично тогда и только тогда, когда
∗
pw (n) ≥ 2n для всех достаточно больших n.
Лекция 5 Комбинаторные сложности и всякая всячина 29/42

56. Низкая сложность Камаэ
Theorem (Kamae, Zamboni, 2002)
Бесконечное слово w не периодично тогда и только тогда, когда
∗
pw (n) ≥ 2n для всех достаточно больших n.
Слова со сложностью 2n: все слова Штурма, простые слова Теплица...
и другие.
Лекция 5 Комбинаторные сложности и всякая всячина 29/42

57. Низкая сложность Камаэ
Theorem (Kamae, Zamboni, 2002)
Бесконечное слово w не периодично тогда и только тогда, когда
∗
pw (n) ≥ 2n для всех достаточно больших n.
Слова со сложностью 2n: все слова Штурма, простые слова Теплица...
и другие.
Theorem (KZ 2002)
Сложность Камаэ слова Туэ-Морса равна 2n .
Лекция 5 Комбинаторные сложности и всякая всячина 29/42

58. Низкая сложность Камаэ
Theorem (Kamae, Zamboni, 2002)
Бесконечное слово w не периодично тогда и только тогда, когда
∗
pw (n) ≥ 2n для всех достаточно больших n.
Слова со сложностью 2n: все слова Штурма, простые слова Теплица...
и другие.
Theorem (KZ 2002)
Сложность Камаэ слова Туэ-Морса равна 2n .
Kamae, Salimov недавно разобрались со сложностью Камаэ
неподвижных точек бинарных однородных морфизмов.
Лекция 5 Комбинаторные сложности и всякая всячина 29/42

59. Перестановки и слова
Пусть a = a0 , a1 , a2 , . . . и b = b0 , b1 , b2 , . . . две последовательности
действительных чисел, и
a ∼ b : ai < aj ⇐⇒ bi < bj
(Конечная или бесконечная) перестановка это класс эквивалентност
α = a = b.
Последовательности a и b представители перестановки α.
Пример: −100, 200, 197 = 90, 100, 98 = 1, 3, 2
Можно писать просто α = 1 3 2, но лучше различать перестановки и
их представители.
Лекция 5 Комбинаторные сложности и всякая всячина 30/42

60. Перестановки, порожденные словами
wTM = 0110100110010110 · · · слово Туэ-Морса
Рассмотрим последователь-
ность aTM сдвигов:
0, 01101001 · · · ,
1
0, 11010010 · · · ,
0, 10100110 · · · ,
0,1
0, 01001100 · · · ,
0, 10011001 · · · ,
0
0, 00110010 · · · , и т.д.
αTM = aTM
Естественно рассматривать перестановки, порожденные бинарными
словами.
Лекция 5 Комбинаторные сложности и всякая всячина 31/42

61. Подперестановки или факторы
По аналогии с подсловами:
011010011001 · · ·
Лекция 5 Комбинаторные сложности и всякая всячина 32/42

62. Подперестановки или факторы
По аналогии с подсловами:
011010011001 · · ·
Лекция 5 Комбинаторные сложности и всякая всячина 33/42

63. Перестановочная сложность
Definition
Перестановочной сложностью tw (n) непериодического бесконечного
слова w называется число подперестановок заданной длины n
порожденной им бесконечной перестановки.
Лекция 5 Комбинаторные сложности и всякая всячина 34/42

64. Свойства перестановочной сложности
Все нижеследующее верно только для бинарных слов!
Лекция 5 Комбинаторные сложности и всякая всячина 35/42

65. Свойства перестановочной сложности
Все нижеследующее верно только для бинарных слов!
tw (n) ≥ pw (n − 1).
Лекция 5 Комбинаторные сложности и всякая всячина 35/42

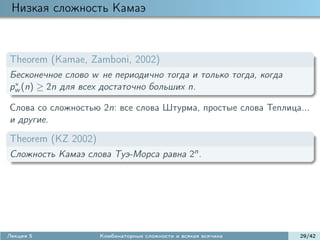
66. Свойства перестановочной сложности
Наибольшая перестановочная сложность бесконечного бинарного
слова равна
n−1
t(n) = ψ(t) · 2n−1−t ,
t=1
где ψ(t) = d|t µ(t/d) · 2d число различных примитивных слов
длины t.
t(n + 1) = 2n (n − α + O(n2−n/2 ); α = 1.3827 · · ·
[Макаров, 2005]
Лекция 5 Комбинаторные сложности и всякая всячина 36/42

67. Свойства перестановочной сложности
Перестановочная сложность слов Штурма равна n, и это
минимум для перестановочной сложности слов.
[Макаров, 2006]
Лекция 5 Комбинаторные сложности и всякая всячина 37/42

68. Свойства перестановочной сложности
Перестановочная сложность слов Штурма равна n, и это
минимум для перестановочной сложности слов.
[Макаров, 2006]
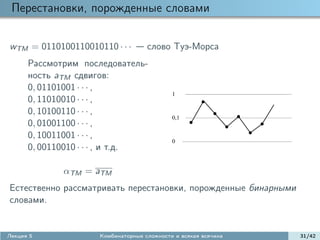
Перестановочная сложность слова Туэ-Морса нашел S. Widmer
(2011); Валюженич успел обобщить.
Лекция 5 Комбинаторные сложности и всякая всячина 37/42

69. Первый дополнительный слайд с красивой картинкой
[Fon-Der-Flaass, Frid, 2005]
Лекция 5 Комбинаторные сложности и всякая всячина 38/42

70. Второй дополнительный слайд с красивой картинкой
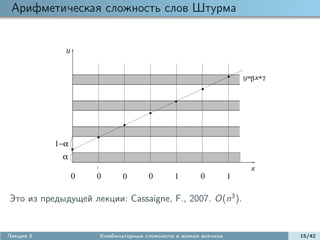
Перестановки Штурма
Фиксируем x, y > 0 и пола-
гаем
ai + x при wi = 0,
ai+1 =
ai − y при wi = 1.
0 1 0 1 0 0 1 0 1 0 1 0
Частный случай:
x = σ, y = 1 − σ
[Макаров, 2006]: это в точности перестановки, порожденные словами
Штурма.
Лекция 5 Комбинаторные сложности и всякая всячина 39/42

71. Низкая сложность Камаэ
Theorem (Avgustinovich, F., Kamae, Salimov, 2011)
Бесконечная перестановка w непериодична тогда и только тогда, когда
∗
pw (n) ≥ n для всех достаточно больших n.
Лекция 5 Комбинаторные сложности и всякая всячина 40/42

72. Низкая сложность Камаэ
Theorem (Avgustinovich, F., Kamae, Salimov, 2011)
Бесконечная перестановка w непериодична тогда и только тогда, когда
∗
pw (n) ≥ n для всех достаточно больших n.
Несомненно, это аналог
Theorem (Kamae, Zamboni, 2002)
Бесконечное слово w не периодично тогда и только тогда, когда
∗
pw (n) ≥ 2n для всех достаточно больших n.
Лекция 5 Комбинаторные сложности и всякая всячина 40/42

73. Низкая сложность Камаэ
Theorem (Avgustinovich, F., Kamae, Salimov, 2011)
Бесконечная перестановка w непериодична тогда и только тогда, когда
∗
pw (n) ≥ n для всех достаточно больших n.
Несомненно, это аналог
Theorem (Kamae, Zamboni, 2002)
Бесконечное слово w не периодично тогда и только тогда, когда
∗
pw (n) ≥ 2n для всех достаточно больших n.
НО! Перестановки со сложностью ровно n это в точности
перестановки Штурма.
Лекция 5 Комбинаторные сложности и всякая всячина 40/42

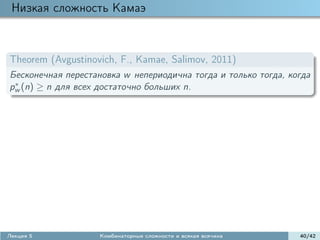
74. Третий красивый слайд
Определим морфизм ϕ : [−1, 1] → [−1, 1]2 :
1 1
2 x, 2x − 1, if x > 0;
ϕ(x) = 1 1
2 x, 2x + 1, if x ≤ 0
1 1 1 3 1 3 1 7 3 5 1 7 3 5
,− , ,− ,− , , ,− ,− , ,− , , ,− ,...
0, 1,
2 2 4 4 4 4 8 8 8 8 8 8 8 8
[Makarov, 2009]
1
0
−1
Лекция 5 Комбинаторные сложности и всякая всячина 41/42

75. Перестановка Туэ-Морса
Два совсем разных представителя!
1
0,1
0
1
0
−1
Лекция 5 Комбинаторные сложности и всякая всячина 42/42