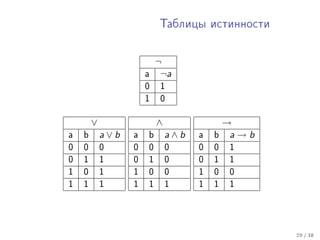
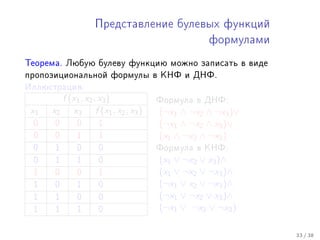
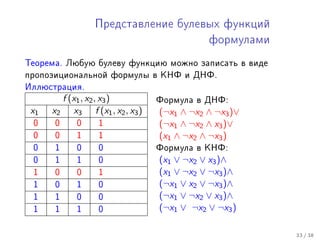
Tài liệu trình bày các khái niệm về độ lớn hàm số, bao gồm các nhóm hàm như poly, exp, và log. Nó giải thích sự so sánh giữa các hàm bằng các ký hiệu o, ω, θ để xác định sự tăng trưởng của chúng. Các định nghĩa và ví dụ được đưa ra để minh họa các quy tắc và mối quan hệ giữa các loại hàm trong toán học.

1. ËÈÊÁÅÇ
Ëåêöèÿ 1: Ìàøèíû Òüþðèíãà. Îñíîâû òåîðèè
âû÷èñëèìîñòè. Áóëåâû ôóíêöèè è
ïðîïîçèöèîíàëüíûå ôîðìóëû
Äìèòðèé Èöûêñîí
ÏÎÌÈ ÐÀÍ
21 ñåíòÿáðÿ 2008
1 / 38

2. Ïëàí
• O -ñèìâîëèêà è àññèìïòîòè÷åñêèå êëàññû ôóíêöèé
• Ìàøèíû Òüþðèíãà
• Ýëåìåíòû òåîðèè âû÷èñëèìîñòè: ðàçðåøèìûå è
ïåðå÷èñëèìûå ÿçûêè
• Áóëåâû ôóíêöèè è ïðîïîçèöèîíàëüíûå ôîðìóëû
2 / 38

3. Ëèòåðàòóðà
1 Í. Ê. Âåðåùàãèí, À. Øåíü. Âû÷èñëèìûå ôóíêöèè.
2 Ò. Êîðìåí, ×. Ëåéçåðñîí, Ð. Ðèâåñò. Àëãîðèòìû.
Ïîñòðîåíèå è àíàëèç.
3 / 38

4. O , o , Ω, Θ
Îáîçíà÷åíèÿ
Ôóíêöèè f , g : N → R+
• f (n) = O(g (n)), åñëè ∃c > 0∃n0 ∀n > n0 , f (n) < cg (n);
• f (n) = o(g (n)), åñëè lim f (n) = 0;
n→∞ g (n)
• f (n) = Ω(g (n)), åñëè ∃c > 0∃n0 ∀n > n0 , f (n) > cg (n);
• f (n) = Θ(g (n)), åñëè
∃c1 , c2 > 0∃n0 ∀n > n0 , c1 g (n) < f (n) < c2 g (n);
f (n) = O(g (n))
f (n) = Θ(g (n)) ⇐⇒
g (n) = O(f (n))
4 / 38

5. Ïîëåçíî çíàòü
• f (n), g (n) ìíîãî÷ëåíû, deg f = deg g =⇒ f = Θ(g );
• f (n), g (n) ìíîãî÷ëåíû, deg f deg g =⇒ f = o(g );
• log2 n = o(nk );
• log2 n = Θ(loga n) = Θ( êîëè÷åñòâî öèôð â ÷èñëå n);
• nk = o(2n );
• nk = o(nlog n );
• O(1) ýòî êîíñòàíòà;
• o(1) ýòî áåñêîíå÷íî ìàëàÿ ôóíêöèÿ.
5 / 38

6. Êëàññû ôóíêöèé
• poly êëàññ ôóíêöèé íå áîëåå, ÷åì ïîëèíîìèàëüíîãî
ðîñòà.
• f ∈ poly , åñëè ñóùåñòâóåò k ∈ N, ÷òî f = O(nk ).
• Êëàññ poly çàìêíóò îòíîñèòåëüíî ñóììû, ïðîèçâåäåíèÿ è
êîìïîçèöèè ôóíêöèé.
• exp êëàññ ôóíêöèé íå áîëåå, ÷åì ýêñïîíåíöèàëüíîãî
ðîñòà.
• f ∈ exp , åñëè ñóùåñòâóåò g ∈ poly , ÷òî f = O(2g (n) ).
• Êëàññ exp çàìêíóò îíîñèòåëüíî ñóììû, ïðîèçâåäåíèÿ è
êîìïîçèöèåé ñ ýëåìåíòàìè êëàññà poly .
• log êëàññ ôóíêöèé íå áîëåå, ÷åì ëîãàðèôìè÷åñêîãî
ðîñòà.
• f ∈ log , åñëè f = O(logn).
6 / 38

7. Êëàññû ôóíêöèé
• poly êëàññ ôóíêöèé íå áîëåå, ÷åì ïîëèíîìèàëüíîãî
ðîñòà.
• f ∈ poly , åñëè ñóùåñòâóåò k ∈ N, ÷òî f = O(nk ).
• Êëàññ poly çàìêíóò îòíîñèòåëüíî ñóììû, ïðîèçâåäåíèÿ è
êîìïîçèöèè ôóíêöèé.
• exp êëàññ ôóíêöèé íå áîëåå, ÷åì ýêñïîíåíöèàëüíîãî
ðîñòà.
• f ∈ exp , åñëè ñóùåñòâóåò g ∈ poly , ÷òî f = O(2g (n) ).
• Êëàññ exp çàìêíóò îíîñèòåëüíî ñóììû, ïðîèçâåäåíèÿ è
êîìïîçèöèåé ñ ýëåìåíòàìè êëàññà poly .
• log êëàññ ôóíêöèé íå áîëåå, ÷åì ëîãàðèôìè÷åñêîãî
ðîñòà.
• f ∈ log , åñëè f = O(logn).
6 / 38

8. Êëàññû ôóíêöèé
• poly êëàññ ôóíêöèé íå áîëåå, ÷åì ïîëèíîìèàëüíîãî
ðîñòà.
• f ∈ poly , åñëè ñóùåñòâóåò k ∈ N, ÷òî f = O(nk ).
• Êëàññ poly çàìêíóò îòíîñèòåëüíî ñóììû, ïðîèçâåäåíèÿ è
êîìïîçèöèè ôóíêöèé.
• exp êëàññ ôóíêöèé íå áîëåå, ÷åì ýêñïîíåíöèàëüíîãî
ðîñòà.
• f ∈ exp , åñëè ñóùåñòâóåò g ∈ poly , ÷òî f = O(2g (n) ).
• Êëàññ exp çàìêíóò îíîñèòåëüíî ñóììû, ïðîèçâåäåíèÿ è
êîìïîçèöèåé ñ ýëåìåíòàìè êëàññà poly .
• log êëàññ ôóíêöèé íå áîëåå, ÷åì ëîãàðèôìè÷åñêîãî
ðîñòà.
• f ∈ log , åñëè f = O(logn).
6 / 38

9. Êëàññû ôóíêöèé
• poly êëàññ ôóíêöèé íå áîëåå, ÷åì ïîëèíîìèàëüíîãî
ðîñòà.
• f ∈ poly , åñëè ñóùåñòâóåò k ∈ N, ÷òî f = O(nk ).
• Êëàññ poly çàìêíóò îòíîñèòåëüíî ñóììû, ïðîèçâåäåíèÿ è
êîìïîçèöèè ôóíêöèé.
• exp êëàññ ôóíêöèé íå áîëåå, ÷åì ýêñïîíåíöèàëüíîãî
ðîñòà.
• f ∈ exp , åñëè ñóùåñòâóåò g ∈ poly , ÷òî f = O(2g (n) ).
• Êëàññ exp çàìêíóò îíîñèòåëüíî ñóììû, ïðîèçâåäåíèÿ è
êîìïîçèöèåé ñ ýëåìåíòàìè êëàññà poly .
• log êëàññ ôóíêöèé íå áîëåå, ÷åì ëîãàðèôìè÷åñêîãî
ðîñòà.
• f ∈ log , åñëè f = O(logn).
6 / 38

10. Êëàññû ôóíêöèé
• poly êëàññ ôóíêöèé íå áîëåå, ÷åì ïîëèíîìèàëüíîãî
ðîñòà.
• f ∈ poly , åñëè ñóùåñòâóåò k ∈ N, ÷òî f = O(nk ).
• Êëàññ poly çàìêíóò îòíîñèòåëüíî ñóììû, ïðîèçâåäåíèÿ è
êîìïîçèöèè ôóíêöèé.
• exp êëàññ ôóíêöèé íå áîëåå, ÷åì ýêñïîíåíöèàëüíîãî
ðîñòà.
• f ∈ exp , åñëè ñóùåñòâóåò g ∈ poly , ÷òî f = O(2g (n) ).
• Êëàññ exp çàìêíóò îíîñèòåëüíî ñóììû, ïðîèçâåäåíèÿ è
êîìïîçèöèåé ñ ýëåìåíòàìè êëàññà poly .
• log êëàññ ôóíêöèé íå áîëåå, ÷åì ëîãàðèôìè÷åñêîãî
ðîñòà.
• f ∈ log , åñëè f = O(logn).
6 / 38

11. Êëàññû ôóíêöèé
• poly êëàññ ôóíêöèé íå áîëåå, ÷åì ïîëèíîìèàëüíîãî
ðîñòà.
• f ∈ poly , åñëè ñóùåñòâóåò k ∈ N, ÷òî f = O(nk ).
• Êëàññ poly çàìêíóò îòíîñèòåëüíî ñóììû, ïðîèçâåäåíèÿ è
êîìïîçèöèè ôóíêöèé.
• exp êëàññ ôóíêöèé íå áîëåå, ÷åì ýêñïîíåíöèàëüíîãî
ðîñòà.
• f ∈ exp , åñëè ñóùåñòâóåò g ∈ poly , ÷òî f = O(2g (n) ).
• Êëàññ exp çàìêíóò îíîñèòåëüíî ñóììû, ïðîèçâåäåíèÿ è
êîìïîçèöèåé ñ ýëåìåíòàìè êëàññà poly .
• log êëàññ ôóíêöèé íå áîëåå, ÷åì ëîãàðèôìè÷åñêîãî
ðîñòà.
• f ∈ log , åñëè f = O(logn).
6 / 38

12. Êëàññû ôóíêöèé
• poly êëàññ ôóíêöèé íå áîëåå, ÷åì ïîëèíîìèàëüíîãî
ðîñòà.
• f ∈ poly , åñëè ñóùåñòâóåò k ∈ N, ÷òî f = O(nk ).
• Êëàññ poly çàìêíóò îòíîñèòåëüíî ñóììû, ïðîèçâåäåíèÿ è
êîìïîçèöèè ôóíêöèé.
• exp êëàññ ôóíêöèé íå áîëåå, ÷åì ýêñïîíåíöèàëüíîãî
ðîñòà.
• f ∈ exp , åñëè ñóùåñòâóåò g ∈ poly , ÷òî f = O(2g (n) ).
• Êëàññ exp çàìêíóò îíîñèòåëüíî ñóììû, ïðîèçâåäåíèÿ è
êîìïîçèöèåé ñ ýëåìåíòàìè êëàññà poly .
• log êëàññ ôóíêöèé íå áîëåå, ÷åì ëîãàðèôìè÷åñêîãî
ðîñòà.
• f ∈ log , åñëè f = O(logn).
6 / 38

13. Êëàññû ôóíêöèé
• poly êëàññ ôóíêöèé íå áîëåå, ÷åì ïîëèíîìèàëüíîãî
ðîñòà.
• f ∈ poly , åñëè ñóùåñòâóåò k ∈ N, ÷òî f = O(nk ).
• Êëàññ poly çàìêíóò îòíîñèòåëüíî ñóììû, ïðîèçâåäåíèÿ è
êîìïîçèöèè ôóíêöèé.
• exp êëàññ ôóíêöèé íå áîëåå, ÷åì ýêñïîíåíöèàëüíîãî
ðîñòà.
• f ∈ exp , åñëè ñóùåñòâóåò g ∈ poly , ÷òî f = O(2g (n) ).
• Êëàññ exp çàìêíóò îíîñèòåëüíî ñóììû, ïðîèçâåäåíèÿ è
êîìïîçèöèåé ñ ýëåìåíòàìè êëàññà poly .
• log êëàññ ôóíêöèé íå áîëåå, ÷åì ëîãàðèôìè÷åñêîãî
ðîñòà.
• f ∈ log , åñëè f = O(logn).
6 / 38

14. Ìîäåëè âû÷èñëåíèé
Çà÷åì îíè íóæíû?
• Ìàòåìàòè÷åñêîå îïðåäåëåíèå ïîíÿòèÿ àëãîðèòì;
• Ñòðîãîå îïðåäåëåíèå ñëîæíîñòè àëãîðèòìà;
• Âîçìîæíîñòü ÷òî-òî äîêàçûâàòü ïðî âñå àëãîðèòìû.
Äîêàçûâàòü íåâîçìîæíîñòü àëãîðèòìà.
Êàêèå Âû çíàåòå ìîäåëè âû÷èñëåíèÿ?
λ-èñ÷èñëåíèå, ìàøèíà Òüþðèíãà, ÐÀÌ-ìàøèíà, ìàøèíà Ïîñòà,
íîðìàëüíûå àëãîðèòìû Ìàðêîâà...
Ïî÷òè ëþáîé ÿçûê ïðîãðàììèðîâàíèÿ ìîæåò âûñòóïàòü â ðîëè
ìîäåëè âû÷èñëåíèÿ, åñëè åñòü âîçìîæíîñòü èñïîëüçîâàòü
íåîãðàíè÷åííîå êîëè÷åñòâî ïàìÿòè.
7 / 38

15. Ìîäåëè âû÷èñëåíèé
Çà÷åì îíè íóæíû?
• Ìàòåìàòè÷åñêîå îïðåäåëåíèå ïîíÿòèÿ àëãîðèòì;
• Ñòðîãîå îïðåäåëåíèå ñëîæíîñòè àëãîðèòìà;
• Âîçìîæíîñòü ÷òî-òî äîêàçûâàòü ïðî âñå àëãîðèòìû.
Äîêàçûâàòü íåâîçìîæíîñòü àëãîðèòìà.
Êàêèå Âû çíàåòå ìîäåëè âû÷èñëåíèÿ?
λ-èñ÷èñëåíèå, ìàøèíà Òüþðèíãà, ÐÀÌ-ìàøèíà, ìàøèíà Ïîñòà,
íîðìàëüíûå àëãîðèòìû Ìàðêîâà...
Ïî÷òè ëþáîé ÿçûê ïðîãðàììèðîâàíèÿ ìîæåò âûñòóïàòü â ðîëè
ìîäåëè âû÷èñëåíèÿ, åñëè åñòü âîçìîæíîñòü èñïîëüçîâàòü
íåîãðàíè÷åííîå êîëè÷åñòâî ïàìÿòè.
7 / 38

16. Îñíîâíûå îïðåäåëåíèÿ
Àëôàâèò
Àëôàâèò ýòî íåêîòîðîå êîíå÷íîå ìíîæåñòâî ñèìâîëîâ.
Ñòàíäàðòíîå îáîçíà÷åíèå: Σ.
Ñëîâà â àëôàâèòå
Ñëîâî ýòî êîíå÷íàÿ ïîñëåäîâàòåëüíîñòü ñèìâîëîâ. Åñëè Σ
àëôàâèò, òî Σ∗ ìíîæåñòâî âñåõ ñëîâ â àëôàâèòå.
Íàïðèìåð: Σ = {a, b}, òî Σ∗ = {λ, a, b, aa, ab, ba, bb, aaa, . . . },
ãäå λ ïóñòîå ñëîâî.
8 / 38

17. ßçûêè è ôóíêöèè
ßçûê
ßçûêîì íàä àëôàâèòîì Σ íàçûâàåòñÿ ïîäìíîæåñòâî Σ∗ .
Ïðèìåðû ÿçûêîâ
ßçûê ïðîñòûõ ÷èñåë, ÿçûê ÷åòíûõ ÷èñåë, ÿçûê äâóäîëüíûõ
ãðàôîâ, ÿçûê âûïîëíèìûõ ôîðìóë â ÊÍÔ è ò.ä.
Ñîãëàøåíèå
Ñ÷èòàåì, ÷òî ëþáîé àëãîðèòì ëèáî ïðîâåðÿåò ïðèíàäëåæíîñòü
âõîäíîãî ñëîâà íåêîòîðîìó ÿçûêó, ëèáî âû÷èñëÿåò çíà÷åíèå
ôóíêöèè Σ∗ → Σ∗ .
9 / 38

18. Ìàøèíà Òüþðèíãà
• Áåñêîíå÷íàÿ â îäíó ñòîðîíó ëåíòà, ðàçäåëåííàÿ íà ÿ÷åéêè.
 ñàìîé ëåâîé ÿ÷åéêå íàïèñàí ñèìâîë .
• Q êîíå÷íîå ìíîæåñòâî ñîñòîÿíèé. q0 ∈ Q íà÷àëüíîå
ñîñòîÿíèå. qf ∈ Q êîíå÷íîå ñîñòîÿíèå.
• Σ àëôàâèò ñèìâîëîâ, êîòîðûå ìîãóò áûòü çàïèñàíû íà
ëåíòå. , ”_” ∈ Σ.
• Ãîëîâêà ìàøèíû óêàçûâàåò íà îäíó èç ÿ÷ååê ëåíòû
• Ïðàâèëî ïåðåõîäà: δ : Σ × Q → Σ × Q × {→, ←, •}
• Ñîãëàñíî ïðàâèëó ïåðåõîäà ìàøèíà ïî ñèìâîëó, íà
êîòîðûé óêàçûâàåò ãîëîâêà, è ïî òåêóùåìó ñîñòîÿíèþ,
ïèøåò íà ýòî ìåñòî íîâûé ñèìâîë, ïåðåõîäèò â íîâîå
ñîñòîÿíèå è, âîçìîæíî, ñäâèãàåò ãîëîâêó íà 1 ñèìâîë
âëåâî èëè âïðàâî.
• Íà÷èíàåò ðàáîòó â ñîñòîÿíèè q0 , ãîëîâêà óêàçûâàåò íà
ïåðâûé ñèìâîë. Çàêàí÷èâàåò â ñîñòîÿíèè qf .
10 / 38

19. Ïðèìåð
Çàìåíèòü ÷èñëî â äâîè÷íîé ñèñòåìå ñ÷èñëåíèÿ íà åãî
îñòàòîê ïðè äåëåíèè íà 2.
• (q0 , 0 ) → (q0 , 0 , →);
1 1
• (q0 , _) → (q1 , _, ←);
• (q1 , 0) → (q2 , _, ←);
• (q1 , 1) → (q3 , _, ←);
• ( q2 , 0 ) → ( q2 , _, ←);
q3 1 q3
• ( q2 , ) → ( q2 , , →);
q3 q3
• (q2 , _) → (qf , 0, •);
• (q3 , _) → (qf , 1, •).
11 / 38

20. Ïðèìåð
Äåëèòñÿ ëè ÷èñëî â 2-îé ñèñòåìå ñ÷èñëåíèÿ íà 3?
• (q0 , 0) → (q0 , 0, →);
• (q0 , 1) → (q1 , 1, →);
• (q1 , 0) → (q2 , 0, →);
• (q1 , 1) → (q0 , 1, →);
• (q2 , 0) → (q1 , 0, →);
• (q2 , 1) → (q2 , 1, →);
• (q0 , _) → (qyes , _, •);
• (q1 , _) → (qno , _, •);
• (q2 , _) → (qno , _, •).
12 / 38

21. Ìàøèíà Òüþðèíãà
Âõîä ìàøèíû Òüþðèíãà òî, ÷òî çàïèñàíî íà ëåíòå. Çà
âõîäîì ñëåäóåò áåñêîíå÷íîå ÷èñëî ïðîáåëîâ.
Âûõîä ìàøèíû Òüþðèíãà òî, ÷òî çàïèñàíî íà ëåíòå ïîñëå
òîãî, êàê ìàøèíà ïðèøëà â êîíå÷íîå ñîñòîÿíèå.
Åñëè ìàøèíà Òüþðèíãà ïðîâåðÿåò ïðèíàäëåæíîñòü ÿçûêó, òî
óäîáíî èìåòü äâà êîíå÷íûõ ñîñòîÿíèÿ: qyes è qno .
Ìàøèíà Òüþðèíãà ìîæåò:
• çàêîí÷èòü ðàáîòó;
• ðàáîòàòü áåñêîíå÷íî.
13 / 38

22. Ñëîæíîñòíûå ïàðàìåòðû
Âðåìÿ
• Âðåìåíåì ðàáîòû ìàøèíû Òüþðèíãà íà âõîäå x íàçûâàåì
êîëè÷åñòâî øàãîâ, êîòîðîå ìàøèíà äåëàåò, ÷òîáû ïðèéòè â
êîíå÷íîå ñîñòîÿíèå.
• Âðåìåííîé ñëîæíîñòüþ ìàøèíû Òüþðèíãà íàçûâàåì
ìàêñèìóì ïî âñåì âõîäàì äëèíû n âðåìåíè ðàáîòû
ìàøèíû íà ýòèõ âõîäàõ.
Ïàìÿòü
• Ñëîæíîñòüþ ïî ïàìÿòè ðàáîòû ìàøèíû Òüþðèíãà íà
âõîäå x íàçûâàåì êîëè÷åñòâî ÿ÷ååê, â êîòîðûõ ïîáûâàëà
ãîëîâêà ìàøèíû.
• Åìêîñòíîé ñëîæíîñòüþ ìàøèíû Òüþðèíãà íàçûâàåì
ìàêñèìóì ïî âñåì âõîäàì äëèíû n ñëîæíîñòè ïî ïàìÿòè
ðàáîòû ìàøèíû íà ýòèõ âõîäàõ.
14 / 38

23. Ìíîãîëåíòî÷íàÿ ìàøèíà Òüþðèíãà
Åñòü k ëåíò, ãîëîâêà åñòü íà êàæäîé ëåíòå.
Ïðàâèëî ïåðåõîäà: δ : Σk × Q → Σk × Q × {→, ←, •}k
Ôàêò
Ïî ëþáîé ìíîãîëåíòî÷íîé ìàøèíå Òüþðèíãà ìîæíî ïîñòðîèòü
îäíîëåíòî÷íóþ ìàøèíó Òüþðèíãà, âû÷èñëÿþùóþ òó æå
ôóíêöèþ. Ïðè÷åì ñëîæíîñòíûå õàðàêòåðèñòèêè ýòîé ìàøèíû
áóäóò ëèøü â ïîëèíîì ðàç õóæå.
Çàìå÷àíèå
Èíîãäà óäîáíî ñ÷èòàòü, ÷òî ìàøèíà ñíàáæåíà ñïåöèàëüíîé
âõîäíîé ëåíòîé, äîñòóïíîé òîëüêî äëÿ ÷òåíèÿ è âûõîäíîé
ëåíòîé, äîñòóïíîé äëÿ çàïèñè, íî áåç èñïðàâëåíèé.
15 / 38

24. Íåäåòåðìèíèðîâàííàÿ ìàøèíà Òüþðèíãà
• Ïðàâèëà ïåðåõîäà íåîäíîçíà÷íû. Âîçìîæíî, ÷òî
ñóùåñòâóåò íåñêîëüêî ïðàâèë äëÿ îäíîé ïàðû (ñèìâîë,
ñîñòîÿíèå);
• ÍÌÒ ïðèíèìàåò ñëîâî x, åñëè ñóùåñòâóåò
ïîñëåäîâàòåëüíîñòü ëåãàëüíûõ øàãîâ, ïðèâîäÿùèõ â
ñîñòîÿíèå qyes ;
• Îïðåäåëåíèå íå ñèììåòðè÷íî îòíîñèòåëüíî îòâåòîâ yes è
no ;
• Ìîæíî ñ÷èòàòü, ÷òî ìàøèíà ñíàáæåíà äîïîëíèòåëüíîé
ëåíòîé, äîñòóïíîé òîëüêî äëÿ ÷òåíèÿ ñëåâà íàïðàâî. Íà
ýòîé ëåíòå çàïèñàíà ïîäñêàçêà (êàêîå èç ïðàâèë ñåé÷àñ
ïðèìåíÿòü). Ìàøèíà ïðèíèìàåò x, åñëè ñóùåñòâóåò
ïîäñêàçêà, ñ êîòîðîé îíà ïîïàäåò â ñîñòîÿíèå qyes ;
• Ìîæíî äîêàçàòü, ÷òî åñëè íåêîòîðàÿ ÍÌÒ ïðîâåðÿåò
ïðèíàäëåæíîñòü ÿçûêó L, òî ñóùåñòâóåò è
äåòåðìèíèðîâàííàÿ ÌÒ, ïðîâåðÿþùàÿ ïðèíàäëåæíîñòü
ÿçûêó L. 16 / 38

25. Íåäåòåðìèíèðîâàííàÿ ìàøèíà Òüþðèíãà
• Ïðàâèëà ïåðåõîäà íåîäíîçíà÷íû. Âîçìîæíî, ÷òî
ñóùåñòâóåò íåñêîëüêî ïðàâèë äëÿ îäíîé ïàðû (ñèìâîë,
ñîñòîÿíèå);
• ÍÌÒ ïðèíèìàåò ñëîâî x, åñëè ñóùåñòâóåò
ïîñëåäîâàòåëüíîñòü ëåãàëüíûõ øàãîâ, ïðèâîäÿùèõ â
ñîñòîÿíèå qyes ;
• Îïðåäåëåíèå íå ñèììåòðè÷íî îòíîñèòåëüíî îòâåòîâ yes è
no ;
• Ìîæíî ñ÷èòàòü, ÷òî ìàøèíà ñíàáæåíà äîïîëíèòåëüíîé
ëåíòîé, äîñòóïíîé òîëüêî äëÿ ÷òåíèÿ ñëåâà íàïðàâî. Íà
ýòîé ëåíòå çàïèñàíà ïîäñêàçêà (êàêîå èç ïðàâèë ñåé÷àñ
ïðèìåíÿòü). Ìàøèíà ïðèíèìàåò x, åñëè ñóùåñòâóåò
ïîäñêàçêà, ñ êîòîðîé îíà ïîïàäåò â ñîñòîÿíèå qyes ;
• Ìîæíî äîêàçàòü, ÷òî åñëè íåêîòîðàÿ ÍÌÒ ïðîâåðÿåò
ïðèíàäëåæíîñòü ÿçûêó L, òî ñóùåñòâóåò è
äåòåðìèíèðîâàííàÿ ÌÒ, ïðîâåðÿþùàÿ ïðèíàäëåæíîñòü
ÿçûêó L. 16 / 38

26. Íåäåòåðìèíèðîâàííàÿ ìàøèíà Òüþðèíãà
• Ïðàâèëà ïåðåõîäà íåîäíîçíà÷íû. Âîçìîæíî, ÷òî
ñóùåñòâóåò íåñêîëüêî ïðàâèë äëÿ îäíîé ïàðû (ñèìâîë,
ñîñòîÿíèå);
• ÍÌÒ ïðèíèìàåò ñëîâî x, åñëè ñóùåñòâóåò
ïîñëåäîâàòåëüíîñòü ëåãàëüíûõ øàãîâ, ïðèâîäÿùèõ â
ñîñòîÿíèå qyes ;
• Îïðåäåëåíèå íå ñèììåòðè÷íî îòíîñèòåëüíî îòâåòîâ yes è
no ;
• Ìîæíî ñ÷èòàòü, ÷òî ìàøèíà ñíàáæåíà äîïîëíèòåëüíîé
ëåíòîé, äîñòóïíîé òîëüêî äëÿ ÷òåíèÿ ñëåâà íàïðàâî. Íà
ýòîé ëåíòå çàïèñàíà ïîäñêàçêà (êàêîå èç ïðàâèë ñåé÷àñ
ïðèìåíÿòü). Ìàøèíà ïðèíèìàåò x, åñëè ñóùåñòâóåò
ïîäñêàçêà, ñ êîòîðîé îíà ïîïàäåò â ñîñòîÿíèå qyes ;
• Ìîæíî äîêàçàòü, ÷òî åñëè íåêîòîðàÿ ÍÌÒ ïðîâåðÿåò
ïðèíàäëåæíîñòü ÿçûêó L, òî ñóùåñòâóåò è
äåòåðìèíèðîâàííàÿ ÌÒ, ïðîâåðÿþùàÿ ïðèíàäëåæíîñòü
ÿçûêó L. 16 / 38

27. Íåäåòåðìèíèðîâàííàÿ ìàøèíà Òüþðèíãà
• Ïðàâèëà ïåðåõîäà íåîäíîçíà÷íû. Âîçìîæíî, ÷òî
ñóùåñòâóåò íåñêîëüêî ïðàâèë äëÿ îäíîé ïàðû (ñèìâîë,
ñîñòîÿíèå);
• ÍÌÒ ïðèíèìàåò ñëîâî x, åñëè ñóùåñòâóåò
ïîñëåäîâàòåëüíîñòü ëåãàëüíûõ øàãîâ, ïðèâîäÿùèõ â
ñîñòîÿíèå qyes ;
• Îïðåäåëåíèå íå ñèììåòðè÷íî îòíîñèòåëüíî îòâåòîâ yes è
no ;
• Ìîæíî ñ÷èòàòü, ÷òî ìàøèíà ñíàáæåíà äîïîëíèòåëüíîé
ëåíòîé, äîñòóïíîé òîëüêî äëÿ ÷òåíèÿ ñëåâà íàïðàâî. Íà
ýòîé ëåíòå çàïèñàíà ïîäñêàçêà (êàêîå èç ïðàâèë ñåé÷àñ
ïðèìåíÿòü). Ìàøèíà ïðèíèìàåò x, åñëè ñóùåñòâóåò
ïîäñêàçêà, ñ êîòîðîé îíà ïîïàäåò â ñîñòîÿíèå qyes ;
• Ìîæíî äîêàçàòü, ÷òî åñëè íåêîòîðàÿ ÍÌÒ ïðîâåðÿåò
ïðèíàäëåæíîñòü ÿçûêó L, òî ñóùåñòâóåò è
äåòåðìèíèðîâàííàÿ ÌÒ, ïðîâåðÿþùàÿ ïðèíàäëåæíîñòü
ÿçûêó L. 16 / 38

28. Íåäåòåðìèíèðîâàííàÿ ìàøèíà Òüþðèíãà
• Ïðàâèëà ïåðåõîäà íåîäíîçíà÷íû. Âîçìîæíî, ÷òî
ñóùåñòâóåò íåñêîëüêî ïðàâèë äëÿ îäíîé ïàðû (ñèìâîë,
ñîñòîÿíèå);
• ÍÌÒ ïðèíèìàåò ñëîâî x, åñëè ñóùåñòâóåò
ïîñëåäîâàòåëüíîñòü ëåãàëüíûõ øàãîâ, ïðèâîäÿùèõ â
ñîñòîÿíèå qyes ;
• Îïðåäåëåíèå íå ñèììåòðè÷íî îòíîñèòåëüíî îòâåòîâ yes è
no ;
• Ìîæíî ñ÷èòàòü, ÷òî ìàøèíà ñíàáæåíà äîïîëíèòåëüíîé
ëåíòîé, äîñòóïíîé òîëüêî äëÿ ÷òåíèÿ ñëåâà íàïðàâî. Íà
ýòîé ëåíòå çàïèñàíà ïîäñêàçêà (êàêîå èç ïðàâèë ñåé÷àñ
ïðèìåíÿòü). Ìàøèíà ïðèíèìàåò x, åñëè ñóùåñòâóåò
ïîäñêàçêà, ñ êîòîðîé îíà ïîïàäåò â ñîñòîÿíèå qyes ;
• Ìîæíî äîêàçàòü, ÷òî åñëè íåêîòîðàÿ ÍÌÒ ïðîâåðÿåò
ïðèíàäëåæíîñòü ÿçûêó L, òî ñóùåñòâóåò è
äåòåðìèíèðîâàííàÿ ÌÒ, ïðîâåðÿþùàÿ ïðèíàäëåæíîñòü
ÿçûêó L. 16 / 38

29. Ñëîæíîñòíûå ïàðàìåòðû ÍÌÒ
Âðåìÿ è ïàìÿòü ÍÌÒ ñ÷èòàþòñÿ, êàê ìàêñèìóì ïî âñåì
âàðèàíòàì ïðèìåíåíèÿ ïðàâèëà äî ïðèõîäà â êîíå÷íîå
ñîñòîÿíèå. Åñëè ìàøèíà íå îñòàíàâëèâàåòñÿ ïðè êàêîì-òî
âûáîðå ïðàâèë, òî âðåìÿ ðàáîòû ñ÷èòàåòñÿ áåñêîíå÷íûì.
17 / 38

30. Òåçèñ ×åð÷à-Òüþðèíãà
Ëþáîé àëãîðèòì ìîæíî ðåàëèçîâàòü â âèäå ìàøèíû Òüþðèíãà.
18 / 38

31. Ýëåìåíòû òåîðèè âû÷èñëèìîñòè
• Ìàøèíó Òüþðèíãà ìîæíî çàïèñàòü: àëôàâèò, ñîñòîÿíèÿ,
ïðàâèëà... Êàæäîé ÌÒ ñîîòâåòñòâóåò ñòðî÷êà â íåêîòîðîì
àëôàâèòå.
• Ìàøèí Òüþðèíãà ñ÷åòíîå ÷èñëî.
• Óíèâåðñàëüíàÿ ìàøèíà Òüþðèíãà. Ñóùåñòâóåò òàêàÿ
ìàøèíà Òüþðèíãà U, êîòîðàÿ ïî çàïèñè ìàøèíû
Òüþðèíãà M è âõîäó x ìîäåëèðóåò ïîâåäåíèå ìàøèíû M
íà âõîäå x. Ïðè ýòîì ñëîæíîñòíûå ïàðàìåòðû ìàøèíû U
íå áîëåå, ÷åì â ïîëèíîì îò çàïèñè M è |x| õóæå.
19 / 38

32. Ýëåìåíòû òåîðèè âû÷èñëèìîñòè
• Ìàøèíó Òüþðèíãà ìîæíî çàïèñàòü: àëôàâèò, ñîñòîÿíèÿ,
ïðàâèëà... Êàæäîé ÌÒ ñîîòâåòñòâóåò ñòðî÷êà â íåêîòîðîì
àëôàâèòå.
• Ìàøèí Òüþðèíãà ñ÷åòíîå ÷èñëî.
• Óíèâåðñàëüíàÿ ìàøèíà Òüþðèíãà. Ñóùåñòâóåò òàêàÿ
ìàøèíà Òüþðèíãà U, êîòîðàÿ ïî çàïèñè ìàøèíû
Òüþðèíãà M è âõîäó x ìîäåëèðóåò ïîâåäåíèå ìàøèíû M
íà âõîäå x. Ïðè ýòîì ñëîæíîñòíûå ïàðàìåòðû ìàøèíû U
íå áîëåå, ÷åì â ïîëèíîì îò çàïèñè M è |x| õóæå.
19 / 38

33. Ýëåìåíòû òåîðèè âû÷èñëèìîñòè
• Ìàøèíó Òüþðèíãà ìîæíî çàïèñàòü: àëôàâèò, ñîñòîÿíèÿ,
ïðàâèëà... Êàæäîé ÌÒ ñîîòâåòñòâóåò ñòðî÷êà â íåêîòîðîì
àëôàâèòå.
• Ìàøèí Òüþðèíãà ñ÷åòíîå ÷èñëî.
• Óíèâåðñàëüíàÿ ìàøèíà Òüþðèíãà. Ñóùåñòâóåò òàêàÿ
ìàøèíà Òüþðèíãà U, êîòîðàÿ ïî çàïèñè ìàøèíû
Òüþðèíãà M è âõîäó x ìîäåëèðóåò ïîâåäåíèå ìàøèíû M
íà âõîäå x. Ïðè ýòîì ñëîæíîñòíûå ïàðàìåòðû ìàøèíû U
íå áîëåå, ÷åì â ïîëèíîì îò çàïèñè M è |x| õóæå.
19 / 38

34. Ðàçðåøèìûå è ïåðå÷èñëèìûå ÿçûêè
Σ àëôàâèò, L ⊂ Σ∗ ÿçûê.
ßçûê L íàçûâàåòñÿ àëãîðèòìè÷åñêè ðàçðåøèìûì, åñëè
ñóùåñòâóåò òàêàÿ ìàøèíà Òüþðèíãà M, ÷òî
x ∈ L ⇐⇒ M(x) îñòàíàâëèâàåòñÿ â ñîñòîÿíèè qyes
x ∈ L ⇐⇒ M(x) îñòàíàâëèâàåòñÿ â ñîñòîÿíèè qno
ßçûê L íàçûâàåòñÿ ïåðå÷èñëèìûì, åñëè ñóùåñòâóåò òàêàÿ
ìàøèíà Òüþðèíãà M, ÷òî
x ∈ L ⇐⇒ M(x) îñòàíàâëèâàåòñÿ â ñîñòîÿíèè qyes
x ∈ L ⇐⇒ M(x) íå îñòàíàâëèâàåòñÿ
20 / 38

35. Ðàçðåøèìûå è ïåðå÷èñëèìûå ÿçûêè
Σ àëôàâèò, L ⊂ Σ∗ ÿçûê.
ßçûê L íàçûâàåòñÿ àëãîðèòìè÷åñêè ðàçðåøèìûì, åñëè
ñóùåñòâóåò òàêàÿ ìàøèíà Òüþðèíãà M, ÷òî
x ∈ L ⇐⇒ M(x) îñòàíàâëèâàåòñÿ â ñîñòîÿíèè qyes
x ∈ L ⇐⇒ M(x) îñòàíàâëèâàåòñÿ â ñîñòîÿíèè qno
ßçûê L íàçûâàåòñÿ ïåðå÷èñëèìûì, åñëè ñóùåñòâóåò òàêàÿ
ìàøèíà Òüþðèíãà M, ÷òî
x ∈ L ⇐⇒ M(x) îñòàíàâëèâàåòñÿ â ñîñòîÿíèè qyes
x ∈ L ⇐⇒ M(x) íå îñòàíàâëèâàåòñÿ
20 / 38

36. Ïðîñòåéøèå ñâîéñòâà
Ëåììà 1
Ëþáîé ðàçðåøèìûé ÿçûê ÿâëÿåòñÿ ïåðå÷èñëèìûì.
Äîñòàòî÷íî ñîñòîÿíèå qno çàìåíèòü íà q∞ è äîáàâèòü ïðàâèëà
(q∞ , ∗) → (q∞ , ∗, →)
Ëåììà 2
ßçûê L ïåðå÷èñëèì ⇐⇒ ñóùåñòâóåò ÌÒ M , êîòîðàÿ,
ðàáîòàÿ íà ïóñòîì âõîäå, ðàíî èëè ïîçäíî íàïå÷àòàåò ëþáîé
ýëåìåíò ÿçûêà L áåç ïîâòîðåíèé. (Ìàøèíà M ìîæåò ðàáîòàòü
áåñêîíå÷íî äîëãî).
⇐ Ìàøèíà M áóäåò æäàòü, ïîêà M íàïå÷àòàåò ñëîâî x.
⇒ M ìîäåëèðóåò M : 1 øàã íà ïåðâîì âõîäå, 2 øàãà íà
ïåðâîì, 2 øàãà íà âòîðîì, 3 øàãà íà ïåðâîì, âòîðîì, òðåòüåì,
4 øàãà...
21 / 38

37. Ïðîñòåéøèå ñâîéñòâà
Ëåììà 1
Ëþáîé ðàçðåøèìûé ÿçûê ÿâëÿåòñÿ ïåðå÷èñëèìûì.
Äîñòàòî÷íî ñîñòîÿíèå qno çàìåíèòü íà q∞ è äîáàâèòü ïðàâèëà
(q∞ , ∗) → (q∞ , ∗, →)
Ëåììà 2
ßçûê L ïåðå÷èñëèì ⇐⇒ ñóùåñòâóåò ÌÒ M , êîòîðàÿ,
ðàáîòàÿ íà ïóñòîì âõîäå, ðàíî èëè ïîçäíî íàïå÷àòàåò ëþáîé
ýëåìåíò ÿçûêà L áåç ïîâòîðåíèé. (Ìàøèíà M ìîæåò ðàáîòàòü
áåñêîíå÷íî äîëãî).
⇐ Ìàøèíà M áóäåò æäàòü, ïîêà M íàïå÷àòàåò ñëîâî x.
⇒ M ìîäåëèðóåò M : 1 øàã íà ïåðâîì âõîäå, 2 øàãà íà
ïåðâîì, 2 øàãà íà âòîðîì, 3 øàãà íà ïåðâîì, âòîðîì, òðåòüåì,
4 øàãà...
21 / 38

38. Ïðîñòåéøèå ñâîéñòâà
Ëåììà 1
Ëþáîé ðàçðåøèìûé ÿçûê ÿâëÿåòñÿ ïåðå÷èñëèìûì.
Äîñòàòî÷íî ñîñòîÿíèå qno çàìåíèòü íà q∞ è äîáàâèòü ïðàâèëà
(q∞ , ∗) → (q∞ , ∗, →)
Ëåììà 2
ßçûê L ïåðå÷èñëèì ⇐⇒ ñóùåñòâóåò ÌÒ M , êîòîðàÿ,
ðàáîòàÿ íà ïóñòîì âõîäå, ðàíî èëè ïîçäíî íàïå÷àòàåò ëþáîé
ýëåìåíò ÿçûêà L áåç ïîâòîðåíèé. (Ìàøèíà M ìîæåò ðàáîòàòü
áåñêîíå÷íî äîëãî).
⇐ Ìàøèíà M áóäåò æäàòü, ïîêà M íàïå÷àòàåò ñëîâî x.
⇒ M ìîäåëèðóåò M : 1 øàã íà ïåðâîì âõîäå, 2 øàãà íà
ïåðâîì, 2 øàãà íà âòîðîì, 3 øàãà íà ïåðâîì, âòîðîì, òðåòüåì,
4 øàãà...
21 / 38

39. Ïðîñòåéøèå ñâîéñòâà
Ëåììà 1
Ëþáîé ðàçðåøèìûé ÿçûê ÿâëÿåòñÿ ïåðå÷èñëèìûì.
Äîñòàòî÷íî ñîñòîÿíèå qno çàìåíèòü íà q∞ è äîáàâèòü ïðàâèëà
(q∞ , ∗) → (q∞ , ∗, →)
Ëåììà 2
ßçûê L ïåðå÷èñëèì ⇐⇒ ñóùåñòâóåò ÌÒ M , êîòîðàÿ,
ðàáîòàÿ íà ïóñòîì âõîäå, ðàíî èëè ïîçäíî íàïå÷àòàåò ëþáîé
ýëåìåíò ÿçûêà L áåç ïîâòîðåíèé. (Ìàøèíà M ìîæåò ðàáîòàòü
áåñêîíå÷íî äîëãî).
⇐ Ìàøèíà M áóäåò æäàòü, ïîêà M íàïå÷àòàåò ñëîâî x.
⇒ M ìîäåëèðóåò M : 1 øàã íà ïåðâîì âõîäå, 2 øàãà íà
ïåðâîì, 2 øàãà íà âòîðîì, 3 øàãà íà ïåðâîì, âòîðîì, òðåòüåì,
4 øàãà...
21 / 38

40. Ïðîñòåéøèå ñâîéñòâà
Ëåììà 3
Åñëè ÿçûê L è åãî äîïîëíåíèå L = Σ∗ L ïåðå÷èñëèìû, òî L
àëãîðèòìè÷åñêè ðàçðåøèì.
Ïàðàëëåëüíî çàïóñêàåì àëãîðèòì äëÿ L è L, îäèí èç íèõ
äîëæåí îñòàíîâèòüñÿ.
22 / 38

41. Ïðîñòåéøèå ñâîéñòâà
Ëåììà 3
Åñëè ÿçûê L è åãî äîïîëíåíèå L = Σ∗ L ïåðå÷èñëèìû, òî L
àëãîðèòìè÷åñêè ðàçðåøèì.
Ïàðàëëåëüíî çàïóñêàåì àëãîðèòì äëÿ L è L, îäèí èç íèõ
äîëæåí îñòàíîâèòüñÿ.
22 / 38

42. Âîïðîñû
Ñóùåñòâóþò ëè íåïåðå÷èñëèìûå ÿçûêè?
Ñóùåñòâóþò, òàê êàê ìàøèí Òüþðèíãà ñ÷åòíî, à ÿçûêîâ
êîíòèíóóì.
Íåêîíñòðóêòèâíîå äîêàçàòåëüñòâî
Ñóùåñòâóþò ëè àëãîðèòìè÷åñêè íåðàçðåøèìûå, íî
ïåðå÷èñëèìûå ÿçûêè?
Äà.
23 / 38

43. Âîïðîñû
Ñóùåñòâóþò ëè íåïåðå÷èñëèìûå ÿçûêè?
Ñóùåñòâóþò, òàê êàê ìàøèí Òüþðèíãà ñ÷åòíî, à ÿçûêîâ
êîíòèíóóì.
Íåêîíñòðóêòèâíîå äîêàçàòåëüñòâî
Ñóùåñòâóþò ëè àëãîðèòìè÷åñêè íåðàçðåøèìûå, íî
ïåðå÷èñëèìûå ÿçûêè?
Äà.
23 / 38

44. Âîïðîñû
Ñóùåñòâóþò ëè íåïåðå÷èñëèìûå ÿçûêè?
Ñóùåñòâóþò, òàê êàê ìàøèí Òüþðèíãà ñ÷åòíî, à ÿçûêîâ
êîíòèíóóì.
Íåêîíñòðóêòèâíîå äîêàçàòåëüñòâî
Ñóùåñòâóþò ëè àëãîðèòìè÷åñêè íåðàçðåøèìûå, íî
ïåðå÷èñëèìûå ÿçûêè?
Äà.
23 / 38

45. Ïðèìåð íåïåðå÷èñëèìîãî ÿçûêà
• Âñå çàïèñè ìàøèí Òüþðèíãà ìîæíî ïåðåíóìåðîâàòü ñ
ïîìîùüþ àëãîðèòìà.
• Çàïèñü n îáîçíà÷àåò ÌÒ ñ íîìåðîì n.
• Ðàññìîòðèì ÿçûê
L = {n| n íå îñòàíàâëèâàåòñÿ íà âõîäå n}
• Ïóñòü L ïåðå÷èñëèì àëãîðèòìîì ñ íîìåðîì k.
• Åñëè k ∈ L, òî k íå îñòàíàâëèâàåòñÿ íà k =⇒ k
íå ïåðå÷èñëÿåò L.
• Åñëè k ∈ L, òî k îñòàíàâëèâàåòñÿ íà k =⇒ k íå
ïåðå÷èñëÿåò L.
• Ïðîòèâîðå÷èå. Çíà÷èò L íå ïåðå÷èñëÿåòñÿ íèêàêèì
àëãîðèòìîì.
• L àëãîðèòìè÷åñêè íåðàçðåøèì.
24 / 38

46. Ïðèìåð íåïåðå÷èñëèìîãî ÿçûêà
• Âñå çàïèñè ìàøèí Òüþðèíãà ìîæíî ïåðåíóìåðîâàòü ñ
ïîìîùüþ àëãîðèòìà.
• Çàïèñü n îáîçíà÷àåò ÌÒ ñ íîìåðîì n.
• Ðàññìîòðèì ÿçûê
L = {n| n íå îñòàíàâëèâàåòñÿ íà âõîäå n}
• Ïóñòü L ïåðå÷èñëèì àëãîðèòìîì ñ íîìåðîì k.
• Åñëè k ∈ L, òî k íå îñòàíàâëèâàåòñÿ íà k =⇒ k
íå ïåðå÷èñëÿåò L.
• Åñëè k ∈ L, òî k îñòàíàâëèâàåòñÿ íà k =⇒ k íå
ïåðå÷èñëÿåò L.
• Ïðîòèâîðå÷èå. Çíà÷èò L íå ïåðå÷èñëÿåòñÿ íèêàêèì
àëãîðèòìîì.
• L àëãîðèòìè÷åñêè íåðàçðåøèì.
24 / 38

47. Ïðèìåð íåïåðå÷èñëèìîãî ÿçûêà
• Âñå çàïèñè ìàøèí Òüþðèíãà ìîæíî ïåðåíóìåðîâàòü ñ
ïîìîùüþ àëãîðèòìà.
• Çàïèñü n îáîçíà÷àåò ÌÒ ñ íîìåðîì n.
• Ðàññìîòðèì ÿçûê
L = {n| n íå îñòàíàâëèâàåòñÿ íà âõîäå n}
• Ïóñòü L ïåðå÷èñëèì àëãîðèòìîì ñ íîìåðîì k.
• Åñëè k ∈ L, òî k íå îñòàíàâëèâàåòñÿ íà k =⇒ k
íå ïåðå÷èñëÿåò L.
• Åñëè k ∈ L, òî k îñòàíàâëèâàåòñÿ íà k =⇒ k íå
ïåðå÷èñëÿåò L.
• Ïðîòèâîðå÷èå. Çíà÷èò L íå ïåðå÷èñëÿåòñÿ íèêàêèì
àëãîðèòìîì.
• L àëãîðèòìè÷åñêè íåðàçðåøèì.
24 / 38

48. Ïðèìåð íåïåðå÷èñëèìîãî ÿçûêà
• Âñå çàïèñè ìàøèí Òüþðèíãà ìîæíî ïåðåíóìåðîâàòü ñ
ïîìîùüþ àëãîðèòìà.
• Çàïèñü n îáîçíà÷àåò ÌÒ ñ íîìåðîì n.
• Ðàññìîòðèì ÿçûê
L = {n| n íå îñòàíàâëèâàåòñÿ íà âõîäå n}
• Ïóñòü L ïåðå÷èñëèì àëãîðèòìîì ñ íîìåðîì k.
• Åñëè k ∈ L, òî k íå îñòàíàâëèâàåòñÿ íà k =⇒ k
íå ïåðå÷èñëÿåò L.
• Åñëè k ∈ L, òî k îñòàíàâëèâàåòñÿ íà k =⇒ k íå
ïåðå÷èñëÿåò L.
• Ïðîòèâîðå÷èå. Çíà÷èò L íå ïåðå÷èñëÿåòñÿ íèêàêèì
àëãîðèòìîì.
• L àëãîðèòìè÷åñêè íåðàçðåøèì.
24 / 38

49. Ïðèìåð íåïåðå÷èñëèìîãî ÿçûêà
• Âñå çàïèñè ìàøèí Òüþðèíãà ìîæíî ïåðåíóìåðîâàòü ñ
ïîìîùüþ àëãîðèòìà.
• Çàïèñü n îáîçíà÷àåò ÌÒ ñ íîìåðîì n.
• Ðàññìîòðèì ÿçûê
L = {n| n íå îñòàíàâëèâàåòñÿ íà âõîäå n}
• Ïóñòü L ïåðå÷èñëèì àëãîðèòìîì ñ íîìåðîì k.
• Åñëè k ∈ L, òî k íå îñòàíàâëèâàåòñÿ íà k =⇒ k
íå ïåðå÷èñëÿåò L.
• Åñëè k ∈ L, òî k îñòàíàâëèâàåòñÿ íà k =⇒ k íå
ïåðå÷èñëÿåò L.
• Ïðîòèâîðå÷èå. Çíà÷èò L íå ïåðå÷èñëÿåòñÿ íèêàêèì
àëãîðèòìîì.
• L àëãîðèòìè÷åñêè íåðàçðåøèì.
24 / 38

50. Ïðèìåð íåïåðå÷èñëèìîãî ÿçûêà
• Âñå çàïèñè ìàøèí Òüþðèíãà ìîæíî ïåðåíóìåðîâàòü ñ
ïîìîùüþ àëãîðèòìà.
• Çàïèñü n îáîçíà÷àåò ÌÒ ñ íîìåðîì n.
• Ðàññìîòðèì ÿçûê
L = {n| n íå îñòàíàâëèâàåòñÿ íà âõîäå n}
• Ïóñòü L ïåðå÷èñëèì àëãîðèòìîì ñ íîìåðîì k.
• Åñëè k ∈ L, òî k íå îñòàíàâëèâàåòñÿ íà k =⇒ k
íå ïåðå÷èñëÿåò L.
• Åñëè k ∈ L, òî k îñòàíàâëèâàåòñÿ íà k =⇒ k íå
ïåðå÷èñëÿåò L.
• Ïðîòèâîðå÷èå. Çíà÷èò L íå ïåðå÷èñëÿåòñÿ íèêàêèì
àëãîðèòìîì.
• L àëãîðèòìè÷åñêè íåðàçðåøèì.
24 / 38

51. Ïðèìåð íåïåðå÷èñëèìîãî ÿçûêà
• Âñå çàïèñè ìàøèí Òüþðèíãà ìîæíî ïåðåíóìåðîâàòü ñ
ïîìîùüþ àëãîðèòìà.
• Çàïèñü n îáîçíà÷àåò ÌÒ ñ íîìåðîì n.
• Ðàññìîòðèì ÿçûê
L = {n| n íå îñòàíàâëèâàåòñÿ íà âõîäå n}
• Ïóñòü L ïåðå÷èñëèì àëãîðèòìîì ñ íîìåðîì k.
• Åñëè k ∈ L, òî k íå îñòàíàâëèâàåòñÿ íà k =⇒ k
íå ïåðå÷èñëÿåò L.
• Åñëè k ∈ L, òî k îñòàíàâëèâàåòñÿ íà k =⇒ k íå
ïåðå÷èñëÿåò L.
• Ïðîòèâîðå÷èå. Çíà÷èò L íå ïåðå÷èñëÿåòñÿ íèêàêèì
àëãîðèòìîì.
• L àëãîðèòìè÷åñêè íåðàçðåøèì.
24 / 38

52. Ïðèìåð íåïåðå÷èñëèìîãî ÿçûêà
• Âñå çàïèñè ìàøèí Òüþðèíãà ìîæíî ïåðåíóìåðîâàòü ñ
ïîìîùüþ àëãîðèòìà.
• Çàïèñü n îáîçíà÷àåò ÌÒ ñ íîìåðîì n.
• Ðàññìîòðèì ÿçûê
L = {n| n íå îñòàíàâëèâàåòñÿ íà âõîäå n}
• Ïóñòü L ïåðå÷èñëèì àëãîðèòìîì ñ íîìåðîì k.
• Åñëè k ∈ L, òî k íå îñòàíàâëèâàåòñÿ íà k =⇒ k
íå ïåðå÷èñëÿåò L.
• Åñëè k ∈ L, òî k îñòàíàâëèâàåòñÿ íà k =⇒ k íå
ïåðå÷èñëÿåò L.
• Ïðîòèâîðå÷èå. Çíà÷èò L íå ïåðå÷èñëÿåòñÿ íèêàêèì
àëãîðèòìîì.
• L àëãîðèòìè÷åñêè íåðàçðåøèì.
24 / 38

53. Ïðèìåð ïåðå÷èñëèìîãî, íî íå
ðàçðåøèìîãî ÿçûêà
• L = {n| n îñòàíàâëèâàåòñÿ íà âõîäå n};
• L íåðàçðåøèì, òàê êàê èíà÷å è ÿçûê L áûë áû
ðàçðåøèìûì;
• L ïåðå÷èñëèì: ìîäåëèðóåì ìàøèíó n íà âõîäå n è
æäåì, ïîêà îíà îñòàíîâèòñÿ.
25 / 38

54. Ïðèìåð ïåðå÷èñëèìîãî, íî íå
ðàçðåøèìîãî ÿçûêà
• L = {n| n îñòàíàâëèâàåòñÿ íà âõîäå n};
• L íåðàçðåøèì, òàê êàê èíà÷å è ÿçûê L áûë áû
ðàçðåøèìûì;
• L ïåðå÷èñëèì: ìîäåëèðóåì ìàøèíó n íà âõîäå n è
æäåì, ïîêà îíà îñòàíîâèòñÿ.
25 / 38

55. Ïðèìåð ïåðå÷èñëèìîãî, íî íå
ðàçðåøèìîãî ÿçûêà
• L = {n| n îñòàíàâëèâàåòñÿ íà âõîäå n};
• L íåðàçðåøèì, òàê êàê èíà÷å è ÿçûê L áûë áû
ðàçðåøèìûì;
• L ïåðå÷èñëèì: ìîäåëèðóåì ìàøèíó n íà âõîäå n è
æäåì, ïîêà îíà îñòàíîâèòñÿ.
25 / 38

56. Êîììåíòàðèé
• Çàäà÷à îñòàíîâêè ÌÒ: ïî ÌÒ è åå âõîäó îïðåäåëèòü,
îñòàíîâèòñÿ îíà èëè íåò. Ýòà çàäà÷à àëãîðèòìè÷åñêè
íåðàçðåøèìà;
• Ìåòîä äîêàçàòåëüñòâà: äèàãîíàëèçàöèÿ;
• Âñå ðåçóëüòàòû îá àëãîðèòìè÷åñêîé íåðàçðåøèìîñòè
èñïîëüçóþò íåðàçðåøèìîñòü çàäà÷è îñòàíîâêè ÌÒ.
Âåëèêàÿ òåîðåìà Ôåðìà
Åñëè áû çàäà÷à îñòàíîâêè áûëà áû ðàçðåøèìà, òî ìîæíî áûëî
áû äîêàçàòü Âåëèêóþ òåîðåìó Ôåðìà òàê:
1 Ìàøèíà M íà ïóñòîì âõîäå ïåðåáèðàåò âñå
x, y , z, n ∈ N, n 2 è îñòàíàâëèâàåòñÿ, åñëè x n + y n = z n .
2 Óçíàåì, îñòàíàâëèâàåòñÿ ëè ìàøèíà M íà ïóñòîì âõîäå.
26 / 38

57. Êîììåíòàðèé
• Çàäà÷à îñòàíîâêè ÌÒ: ïî ÌÒ è åå âõîäó îïðåäåëèòü,
îñòàíîâèòñÿ îíà èëè íåò. Ýòà çàäà÷à àëãîðèòìè÷åñêè
íåðàçðåøèìà;
• Ìåòîä äîêàçàòåëüñòâà: äèàãîíàëèçàöèÿ;
• Âñå ðåçóëüòàòû îá àëãîðèòìè÷åñêîé íåðàçðåøèìîñòè
èñïîëüçóþò íåðàçðåøèìîñòü çàäà÷è îñòàíîâêè ÌÒ.
Âåëèêàÿ òåîðåìà Ôåðìà
Åñëè áû çàäà÷à îñòàíîâêè áûëà áû ðàçðåøèìà, òî ìîæíî áûëî
áû äîêàçàòü Âåëèêóþ òåîðåìó Ôåðìà òàê:
1 Ìàøèíà M íà ïóñòîì âõîäå ïåðåáèðàåò âñå
x, y , z, n ∈ N, n 2 è îñòàíàâëèâàåòñÿ, åñëè x n + y n = z n .
2 Óçíàåì, îñòàíàâëèâàåòñÿ ëè ìàøèíà M íà ïóñòîì âõîäå.
26 / 38

58. Êîììåíòàðèé
• Çàäà÷à îñòàíîâêè ÌÒ: ïî ÌÒ è åå âõîäó îïðåäåëèòü,
îñòàíîâèòñÿ îíà èëè íåò. Ýòà çàäà÷à àëãîðèòìè÷åñêè
íåðàçðåøèìà;
• Ìåòîä äîêàçàòåëüñòâà: äèàãîíàëèçàöèÿ;
• Âñå ðåçóëüòàòû îá àëãîðèòìè÷åñêîé íåðàçðåøèìîñòè
èñïîëüçóþò íåðàçðåøèìîñòü çàäà÷è îñòàíîâêè ÌÒ.
Âåëèêàÿ òåîðåìà Ôåðìà
Åñëè áû çàäà÷à îñòàíîâêè áûëà áû ðàçðåøèìà, òî ìîæíî áûëî
áû äîêàçàòü Âåëèêóþ òåîðåìó Ôåðìà òàê:
1 Ìàøèíà M íà ïóñòîì âõîäå ïåðåáèðàåò âñå
x, y , z, n ∈ N, n 2 è îñòàíàâëèâàåòñÿ, åñëè x n + y n = z n .
2 Óçíàåì, îñòàíàâëèâàåòñÿ ëè ìàøèíà M íà ïóñòîì âõîäå.
26 / 38

59. Êîììåíòàðèé
• Çàäà÷à îñòàíîâêè ÌÒ: ïî ÌÒ è åå âõîäó îïðåäåëèòü,
îñòàíîâèòñÿ îíà èëè íåò. Ýòà çàäà÷à àëãîðèòìè÷åñêè
íåðàçðåøèìà;
• Ìåòîä äîêàçàòåëüñòâà: äèàãîíàëèçàöèÿ;
• Âñå ðåçóëüòàòû îá àëãîðèòìè÷åñêîé íåðàçðåøèìîñòè
èñïîëüçóþò íåðàçðåøèìîñòü çàäà÷è îñòàíîâêè ÌÒ.
Âåëèêàÿ òåîðåìà Ôåðìà
Åñëè áû çàäà÷à îñòàíîâêè áûëà áû ðàçðåøèìà, òî ìîæíî áûëî
áû äîêàçàòü Âåëèêóþ òåîðåìó Ôåðìà òàê:
1 Ìàøèíà M íà ïóñòîì âõîäå ïåðåáèðàåò âñå
x, y , z, n ∈ N, n 2 è îñòàíàâëèâàåòñÿ, åñëè x n + y n = z n .
2 Óçíàåì, îñòàíàâëèâàåòñÿ ëè ìàøèíà M íà ïóñòîì âõîäå.
26 / 38

60. Êîììåíòàðèé
• Çàäà÷à îñòàíîâêè ÌÒ: ïî ÌÒ è åå âõîäó îïðåäåëèòü,
îñòàíîâèòñÿ îíà èëè íåò. Ýòà çàäà÷à àëãîðèòìè÷åñêè
íåðàçðåøèìà;
• Ìåòîä äîêàçàòåëüñòâà: äèàãîíàëèçàöèÿ;
• Âñå ðåçóëüòàòû îá àëãîðèòìè÷åñêîé íåðàçðåøèìîñòè
èñïîëüçóþò íåðàçðåøèìîñòü çàäà÷è îñòàíîâêè ÌÒ.
Âåëèêàÿ òåîðåìà Ôåðìà
Åñëè áû çàäà÷à îñòàíîâêè áûëà áû ðàçðåøèìà, òî ìîæíî áûëî
áû äîêàçàòü Âåëèêóþ òåîðåìó Ôåðìà òàê:
1 Ìàøèíà M íà ïóñòîì âõîäå ïåðåáèðàåò âñå
x, y , z, n ∈ N, n 2 è îñòàíàâëèâàåòñÿ, åñëè x n + y n = z n .
2 Óçíàåì, îñòàíàâëèâàåòñÿ ëè ìàøèíà M íà ïóñòîì âõîäå.
26 / 38

61. Êîììåíòàðèé
• Çàäà÷à îñòàíîâêè ÌÒ: ïî ÌÒ è åå âõîäó îïðåäåëèòü,
îñòàíîâèòñÿ îíà èëè íåò. Ýòà çàäà÷à àëãîðèòìè÷åñêè
íåðàçðåøèìà;
• Ìåòîä äîêàçàòåëüñòâà: äèàãîíàëèçàöèÿ;
• Âñå ðåçóëüòàòû îá àëãîðèòìè÷åñêîé íåðàçðåøèìîñòè
èñïîëüçóþò íåðàçðåøèìîñòü çàäà÷è îñòàíîâêè ÌÒ.
Âåëèêàÿ òåîðåìà Ôåðìà
Åñëè áû çàäà÷à îñòàíîâêè áûëà áû ðàçðåøèìà, òî ìîæíî áûëî
áû äîêàçàòü Âåëèêóþ òåîðåìó Ôåðìà òàê:
1 Ìàøèíà M íà ïóñòîì âõîäå ïåðåáèðàåò âñå
x, y , z, n ∈ N, n 2 è îñòàíàâëèâàåòñÿ, åñëè x n + y n = z n .
2 Óçíàåì, îñòàíàâëèâàåòñÿ ëè ìàøèíà M íà ïóñòîì âõîäå.
26 / 38

62. ßçûê ïðîïîçèöèîíàëüíûõ ôîðìóë
Γ áåñêîíå÷íîå ìíîæåñòâî ïðîïîçèöèîíàëüíûõ ïåðåìåííûõ.
Γ = {x1 , x2 , x3 , . . . }.
• Ïðîïîçèöèîíàëüíàÿ ïåðåìåííàÿ ÿâëÿåòñÿ
ïðîïîçèöèîíàëüíîé ôîðìóëîé
• Åñëè A ïðîïîçèöèîíàëüíàÿ ôîðìóëà, òî (A) òîæå
ïðîïîçèöèîíàëüíàÿ ôîðìóëà.
• Åñëè A ïðîïîçèöèîíàëüíàÿ ôîðìóëà, òî ¬A òîæå
ïðîïîçèöèîíàëüíàÿ ôîðìóëà.
• Åñëè A, B ïðîïîçèöèîíàëüíûå ôîðìóëû, òî A∧B
òîæå ïðîïîçèöèîíàëüíàÿ ôîðìóëà.
• Åñëè A, B ïðîïîçèöèîíàëüíûå ôîðìóëû, òî A∨B
òîæå ïðîïîçèöèîíàëüíàÿ ôîðìóëà.
• Åñëè A, B ïðîïîçèöèîíàëüíûå ôîðìóëû, òî A→B
òîæå ïðîïîçèöèîíàëüíàÿ ôîðìóëà.
27 / 38

63. Ïðèìåðû ïðîïîçèöèîíàëüíûõ ôîðìóë
• x1 ;
• x1 ∧ ¬x1 ;
• x1 ∨ ¬x1 ;
• (x1 ∨ x2 ) → x3 ;
• (x1 ∨ ¬x2 ) ∧ (¬x1 ∨ x3 ) ∧ (x3 ∨ x2 );
• (x1 ∧ ¬x2 ) ∨ (¬x1 ∧ x3 ) ∨ (x3 ∧ x2 );
28 / 38

64. Òàáëèöû èñòèííîñòè
¬
a ¬a
0 1
1 0
∨ ∧ →
a b a∨b a b a∧b a b a→b
0 0 0 0 0 0 0 0 1
0 1 1 0 1 0 0 1 1
1 0 1 1 0 0 1 0 0
1 1 1 1 1 1 1 1 1
29 / 38

65. Èíòåðïðåòàöèÿ
Ïóñòü ϕ ïðîïîçèöèîíàëüíàÿ ôîðìóëà ñ ïåðåìåííûìè
x 1 , x2 , . . . , x n .
Èíòåðïðåòàöèåé ôîðìóëû ϕ íàçûâàåòñÿ îòîáðàæåíèå
σ : {x1 , x2 , . . . , xn } → {0, 1}.
Çíà÷åíèå ôîðìóëû Iσ (ϕ) ïðè çàäàííîé èíòåðïðåòàöèè
îïðåäåëÿåòñÿ èíäóêòèâíî ïî ïîñòðîåíèþ ôîðìóëû:
• Iσ (xi ) = σ(xi );
• Iσ ((A)) = Iσ (A);
• Iσ (¬A) = ¬Iσ (A);
• Iσ (A ∧ B) = Iσ (A) ∧ Iσ (B);
• Iσ (A ∨ B) = Iσ (A) ∨ Iσ (B);
• Iσ (A → B) = Iσ (A) → Iσ (B).
30 / 38

66. Áóëåâû ôóíêöèè
Îïðåäåëåíèå. Áóëåâîé ôóíêöèåé ìû íàçûâàåì ôóíêöèþ èç
{0, 1}n â {0, 1}.
Çàìå÷àíèå. Êàæäàÿ ïðîïîçèöèîíàëüíàÿ ôîðìóëà îò n
ïåðåìåííûõ çàäàåò áóëåâó ôóíêöèþ èç {0, 1}n â {0, 1}.
Ïðèìåðû.
• Parity (÷åòíîñòü): f (x1 , x2 , . . . , xn ) = x1 + x2 + · · · + xn mod 2
• Majority (áîëüøèíñòâî):
 n
 1, åñëè x 1 + x2 + · · · + x n ≥
f (x1 , x2 , . . . , xn ) = 2
 0, åñëè x + x + · · · + x n
1 2 n
2
1, åñëè x1 x2 . . . xn − ïðîñòîå ÷èñëî
• f (x1 , x2 , . . . , xn ) =
0, èíà÷å
31 / 38

67. Áóëåâû ôóíêöèè
Îïðåäåëåíèå. Áóëåâîé ôóíêöèåé ìû íàçûâàåì ôóíêöèþ èç
{0, 1}n â {0, 1}.
Çàìå÷àíèå. Êàæäàÿ ïðîïîçèöèîíàëüíàÿ ôîðìóëà îò n
ïåðåìåííûõ çàäàåò áóëåâó ôóíêöèþ èç {0, 1}n â {0, 1}.
Ïðèìåðû.
• Parity (÷åòíîñòü): f (x1 , x2 , . . . , xn ) = x1 + x2 + · · · + xn mod 2
• Majority (áîëüøèíñòâî):
 n
 1, åñëè x 1 + x2 + · · · + x n ≥
f (x1 , x2 , . . . , xn ) = 2
 0, åñëè x + x + · · · + x n
1 2 n
2
1, åñëè x1 x2 . . . xn − ïðîñòîå ÷èñëî
• f (x1 , x2 , . . . , xn ) =
0, èíà÷å
31 / 38

68. Áóëåâû ôóíêöèè
Îïðåäåëåíèå. Áóëåâîé ôóíêöèåé ìû íàçûâàåì ôóíêöèþ èç
{0, 1}n â {0, 1}.
Çàìå÷àíèå. Êàæäàÿ ïðîïîçèöèîíàëüíàÿ ôîðìóëà îò n
ïåðåìåííûõ çàäàåò áóëåâó ôóíêöèþ èç {0, 1}n â {0, 1}.
Ïðèìåðû.
• Parity (÷åòíîñòü): f (x1 , x2 , . . . , xn ) = x1 + x2 + · · · + xn mod 2
• Majority (áîëüøèíñòâî):
 n
 1, åñëè x 1 + x2 + · · · + x n ≥
f (x1 , x2 , . . . , xn ) = 2
 0, åñëè x + x + · · · + x n
1 2 n
2
1, åñëè x1 x2 . . . xn − ïðîñòîå ÷èñëî
• f (x1 , x2 , . . . , xn ) =
0, èíà÷å
31 / 38

69. Áóëåâû ôóíêöèè
Îïðåäåëåíèå. Áóëåâîé ôóíêöèåé ìû íàçûâàåì ôóíêöèþ èç
{0, 1}n â {0, 1}.
Çàìå÷àíèå. Êàæäàÿ ïðîïîçèöèîíàëüíàÿ ôîðìóëà îò n
ïåðåìåííûõ çàäàåò áóëåâó ôóíêöèþ èç {0, 1}n â {0, 1}.
Ïðèìåðû.
• Parity (÷åòíîñòü): f (x1 , x2 , . . . , xn ) = x1 + x2 + · · · + xn mod 2
• Majority (áîëüøèíñòâî):
 n
 1, åñëè x 1 + x2 + · · · + x n ≥
f (x1 , x2 , . . . , xn ) = 2
 0, åñëè x + x + · · · + x n
1 2 n
2
1, åñëè x1 x2 . . . xn − ïðîñòîå ÷èñëî
• f (x1 , x2 , . . . , xn ) =
0, èíà÷å
31 / 38

70. ÊÍÔ è ÄÍÔ
Îïðåäåëåíèå. Ëèòåðàëîì íàçûâàåòñÿ ïðîïîçèöèîíàëüíàÿ
ïåðåìåííàÿ èëè åå îòðèöàíèå: xi , ¬xi .
Îïðåäåëåíèå. Äèçúþíêòîì èëè êëîçîì íàçûâàåòñÿ äèçúþíêöèÿ
íåñêîëüêèõ (âîçìîæíî îäíîãî) ëèòåðàëîâ: (x1 ∨ ¬x2 ∨ x3 ).
Îïðåäåëåíèå. Ôîðìóëîé â ÊÍÔ íàçûâàåòñÿ êîíúþíêöèÿ
íåñêîëüêèõ (âîçìîæíî îäíîãî) äèçúþíêòîâ:
(x1 ∨ ¬x2 ∨ x3 ) ∧ (¬x1 ∨ ¬x3 ) ∧ ¬x1 .
Îïðåäåëåíèå. Êîíúþíêòîì èëè ìîíîìîì íàçûâàåòñÿ
êîíúþíêöèÿ íåñêîëüêèõ (âîçìîæíî îäíîãî) ëèòåðàëîâ:
(x1 ∧ ¬x2 ∧ x3 ).
Îïðåäåëåíèå. Ôîðìóëîé â ÄÍÔ íàçûâàåòñÿ äèçúþíêöèÿ
íåñêîëüêèõ (âîçìîæíî îäíîãî) êîíúþíêòîâ:
(x1 ∧ ¬x2 ∧ x3 ) ∨ (¬x1 ∧ ¬x3 ) ∨ ¬x1 .
32 / 38

71. ÊÍÔ è ÄÍÔ
Îïðåäåëåíèå. Ëèòåðàëîì íàçûâàåòñÿ ïðîïîçèöèîíàëüíàÿ
ïåðåìåííàÿ èëè åå îòðèöàíèå: xi , ¬xi .
Îïðåäåëåíèå. Äèçúþíêòîì èëè êëîçîì íàçûâàåòñÿ äèçúþíêöèÿ
íåñêîëüêèõ (âîçìîæíî îäíîãî) ëèòåðàëîâ: (x1 ∨ ¬x2 ∨ x3 ).
Îïðåäåëåíèå. Ôîðìóëîé â ÊÍÔ íàçûâàåòñÿ êîíúþíêöèÿ
íåñêîëüêèõ (âîçìîæíî îäíîãî) äèçúþíêòîâ:
(x1 ∨ ¬x2 ∨ x3 ) ∧ (¬x1 ∨ ¬x3 ) ∧ ¬x1 .
Îïðåäåëåíèå. Êîíúþíêòîì èëè ìîíîìîì íàçûâàåòñÿ
êîíúþíêöèÿ íåñêîëüêèõ (âîçìîæíî îäíîãî) ëèòåðàëîâ:
(x1 ∧ ¬x2 ∧ x3 ).
Îïðåäåëåíèå. Ôîðìóëîé â ÄÍÔ íàçûâàåòñÿ äèçúþíêöèÿ
íåñêîëüêèõ (âîçìîæíî îäíîãî) êîíúþíêòîâ:
(x1 ∧ ¬x2 ∧ x3 ) ∨ (¬x1 ∧ ¬x3 ) ∨ ¬x1 .
32 / 38

72. ÊÍÔ è ÄÍÔ
Îïðåäåëåíèå. Ëèòåðàëîì íàçûâàåòñÿ ïðîïîçèöèîíàëüíàÿ
ïåðåìåííàÿ èëè åå îòðèöàíèå: xi , ¬xi .
Îïðåäåëåíèå. Äèçúþíêòîì èëè êëîçîì íàçûâàåòñÿ äèçúþíêöèÿ
íåñêîëüêèõ (âîçìîæíî îäíîãî) ëèòåðàëîâ: (x1 ∨ ¬x2 ∨ x3 ).
Îïðåäåëåíèå. Ôîðìóëîé â ÊÍÔ íàçûâàåòñÿ êîíúþíêöèÿ
íåñêîëüêèõ (âîçìîæíî îäíîãî) äèçúþíêòîâ:
(x1 ∨ ¬x2 ∨ x3 ) ∧ (¬x1 ∨ ¬x3 ) ∧ ¬x1 .
Îïðåäåëåíèå. Êîíúþíêòîì èëè ìîíîìîì íàçûâàåòñÿ
êîíúþíêöèÿ íåñêîëüêèõ (âîçìîæíî îäíîãî) ëèòåðàëîâ:
(x1 ∧ ¬x2 ∧ x3 ).
Îïðåäåëåíèå. Ôîðìóëîé â ÄÍÔ íàçûâàåòñÿ äèçúþíêöèÿ
íåñêîëüêèõ (âîçìîæíî îäíîãî) êîíúþíêòîâ:
(x1 ∧ ¬x2 ∧ x3 ) ∨ (¬x1 ∧ ¬x3 ) ∨ ¬x1 .
32 / 38

73. ÊÍÔ è ÄÍÔ
Îïðåäåëåíèå. Ëèòåðàëîì íàçûâàåòñÿ ïðîïîçèöèîíàëüíàÿ
ïåðåìåííàÿ èëè åå îòðèöàíèå: xi , ¬xi .
Îïðåäåëåíèå. Äèçúþíêòîì èëè êëîçîì íàçûâàåòñÿ äèçúþíêöèÿ
íåñêîëüêèõ (âîçìîæíî îäíîãî) ëèòåðàëîâ: (x1 ∨ ¬x2 ∨ x3 ).
Îïðåäåëåíèå. Ôîðìóëîé â ÊÍÔ íàçûâàåòñÿ êîíúþíêöèÿ
íåñêîëüêèõ (âîçìîæíî îäíîãî) äèçúþíêòîâ:
(x1 ∨ ¬x2 ∨ x3 ) ∧ (¬x1 ∨ ¬x3 ) ∧ ¬x1 .
Îïðåäåëåíèå. Êîíúþíêòîì èëè ìîíîìîì íàçûâàåòñÿ
êîíúþíêöèÿ íåñêîëüêèõ (âîçìîæíî îäíîãî) ëèòåðàëîâ:
(x1 ∧ ¬x2 ∧ x3 ).
Îïðåäåëåíèå. Ôîðìóëîé â ÄÍÔ íàçûâàåòñÿ äèçúþíêöèÿ
íåñêîëüêèõ (âîçìîæíî îäíîãî) êîíúþíêòîâ:
(x1 ∧ ¬x2 ∧ x3 ) ∨ (¬x1 ∧ ¬x3 ) ∨ ¬x1 .
32 / 38

74. ÊÍÔ è ÄÍÔ
Îïðåäåëåíèå. Ëèòåðàëîì íàçûâàåòñÿ ïðîïîçèöèîíàëüíàÿ
ïåðåìåííàÿ èëè åå îòðèöàíèå: xi , ¬xi .
Îïðåäåëåíèå. Äèçúþíêòîì èëè êëîçîì íàçûâàåòñÿ äèçúþíêöèÿ
íåñêîëüêèõ (âîçìîæíî îäíîãî) ëèòåðàëîâ: (x1 ∨ ¬x2 ∨ x3 ).
Îïðåäåëåíèå. Ôîðìóëîé â ÊÍÔ íàçûâàåòñÿ êîíúþíêöèÿ
íåñêîëüêèõ (âîçìîæíî îäíîãî) äèçúþíêòîâ:
(x1 ∨ ¬x2 ∨ x3 ) ∧ (¬x1 ∨ ¬x3 ) ∧ ¬x1 .
Îïðåäåëåíèå. Êîíúþíêòîì èëè ìîíîìîì íàçûâàåòñÿ
êîíúþíêöèÿ íåñêîëüêèõ (âîçìîæíî îäíîãî) ëèòåðàëîâ:
(x1 ∧ ¬x2 ∧ x3 ).
Îïðåäåëåíèå. Ôîðìóëîé â ÄÍÔ íàçûâàåòñÿ äèçúþíêöèÿ
íåñêîëüêèõ (âîçìîæíî îäíîãî) êîíúþíêòîâ:
(x1 ∧ ¬x2 ∧ x3 ) ∨ (¬x1 ∧ ¬x3 ) ∨ ¬x1 .
32 / 38

75. Ïðåäñòàâëåíèå áóëåâûõ ôóíêöèé
ôîðìóëàìè
Òåîðåìà. Ëþáóþ áóëåâó ôóíêöèþ ìîæíî çàïèñàòü â âèäå
ïðîïîçèöèîíàëüíîé ôîðìóëû â ÊÍÔ è ÄÍÔ.
Èëëþñòðàöèÿ.
f (x1 , x2 , x3 ) Ôîðìóëà â ÄÍÔ:
x1 x2 x3 f (x1 , x2 , x3 ) (¬x1 ∧ ¬x2 ∧ ¬x3 )∨
0 0 0 1 (¬x1 ∧ ¬x2 ∧ x3 )∨
0 0 1 1 (x1 ∧ ¬x2 ∧ ¬x3 )
0 1 0 0 Ôîðìóëà â ÊÍÔ:
0 1 1 0 (x1 ∨ ¬x2 ∨ x3 )∧
1 0 0 1 (x1 ∨ ¬x2 ∨ ¬x3 )∧
1 0 1 0 (¬x1 ∨ x2 ∨ ¬x3 )∧
1 1 0 0 (¬x1 ∨ ¬x2 ∨ x3 )∧
1 1 1 0 (¬x1 ∨ ¬x2 ∨ ¬x3 )
33 / 38

76. Ïðåäñòàâëåíèå áóëåâûõ ôóíêöèé
ôîðìóëàìè
Òåîðåìà. Ëþáóþ áóëåâó ôóíêöèþ ìîæíî çàïèñàòü â âèäå
ïðîïîçèöèîíàëüíîé ôîðìóëû â ÊÍÔ è ÄÍÔ.
Èëëþñòðàöèÿ.
f (x1 , x2 , x3 ) Ôîðìóëà â ÄÍÔ:
x1 x2 x3 f (x1 , x2 , x3 ) (¬x1 ∧ ¬x2 ∧ ¬x3 )∨
0 0 0 1 (¬x1 ∧ ¬x2 ∧ x3 )∨
0 0 1 1 (x1 ∧ ¬x2 ∧ ¬x3 )
0 1 0 0 Ôîðìóëà â ÊÍÔ:
0 1 1 0 (x1 ∨ ¬x2 ∨ x3 )∧
1 0 0 1 (x1 ∨ ¬x2 ∨ ¬x3 )∧
1 0 1 0 (¬x1 ∨ x2 ∨ ¬x3 )∧
1 1 0 0 (¬x1 ∨ ¬x2 ∨ x3 )∧
1 1 1 0 (¬x1 ∨ ¬x2 ∨ ¬x3 )
33 / 38

77. Ôîðìóëû äå Ìîðãàíà
• çíà÷åíèå ¬(A ∨ B) ñîâïàäàåò ñî çíà÷åíèåì (¬A ∧ ¬B)
• çíà÷åíèå ¬(A ∧ B) ñîâïàäàåò ñî çíà÷åíèåì (¬A ∨ ¬B)
Ñëåäñòâèå. Îòðèöàíèå ôîðìóëû â ÄÍÔ åñòü ôîðìóëà â ÊÍÔ
Äîêàçàòåëüñòâî.
¬((l1,1 ∧ l1,2 ∧ · · · ∧ l1,n1 ) ∨ (l2,1 ∧ l2,2 ∧ · · · ∧ l2,n2 ) ∨ . . .
∨(lk,1 ∧ lk,2 ∧ · · · ∧ lk,nk ))
ìîæíî ïåðåïèñàòü â âèäå
(¬l1,1 ∨ ¬l1,2 ∨ · · · ∨ ¬l1,n1 ) ∧ (¬l2,1 ∨ ¬l2,2 ∧ · · · ∨ ¬l2,n2 ) ∧ . . .
∧(¬lk,1 ∨ ¬lk,2 ∨ · · · ∨ ¬lk,nk )
34 / 38

78. Ôîðìóëû äå Ìîðãàíà
• çíà÷åíèå ¬(A ∨ B) ñîâïàäàåò ñî çíà÷åíèåì (¬A ∧ ¬B)
• çíà÷åíèå ¬(A ∧ B) ñîâïàäàåò ñî çíà÷åíèåì (¬A ∨ ¬B)
Ñëåäñòâèå. Îòðèöàíèå ôîðìóëû â ÄÍÔ åñòü ôîðìóëà â ÊÍÔ
Äîêàçàòåëüñòâî.
¬((l1,1 ∧ l1,2 ∧ · · · ∧ l1,n1 ) ∨ (l2,1 ∧ l2,2 ∧ · · · ∧ l2,n2 ) ∨ . . .
∨(lk,1 ∧ lk,2 ∧ · · · ∧ lk,nk ))
ìîæíî ïåðåïèñàòü â âèäå
(¬l1,1 ∨ ¬l1,2 ∨ · · · ∨ ¬l1,n1 ) ∧ (¬l2,1 ∨ ¬l2,2 ∧ · · · ∨ ¬l2,n2 ) ∧ . . .
∧(¬lk,1 ∨ ¬lk,2 ∨ · · · ∨ ¬lk,nk )
34 / 38

79. Âûïîëíèìîñòü, îáùåçíà÷èìîñòü,
ïðîòèâîðå÷èâîñòü
Îïðåäåëåíèå. Ïðîïîçèöèîíàëüíàÿ ôîðìóëà íàçûâàåòñÿ
âûïîëíèìîé , åñëè ñóùåñòâóåò òàêàÿ èíòåðïðåòàöèÿ, ïðè
êîòîðîé çíà÷åíèå ôîðìóëû ðàâíÿåòñÿ 1.
Îïðåäåëåíèå. Ïðîïîçèöèîíàëüíàÿ ôîðìóëà íàçûâàåòñÿ
íåâûïîëíèìîé (èëè ïðîòèâîðå÷èâîé) , åñëè ïðè âñåõ
èíòåðïðåòàöèÿõ çíà÷åíèå ôîðìóëû ðàâíÿåòñÿ 0.
Îïðåäåëåíèå. Ïðîïîçèöèîíàëüíàÿ ôîðìóëà íàçûâàåòñÿ
îáùåçíà÷èìîé (èëè òàâòîëîãèåé) , åñëè ïðè âñåõ
èíòåðïðåòàöèÿõ çíà÷åíèå ôîðìóëû ðàâíÿåòñÿ 1.
Îïðåäåëåíèå. Ïðîïîçèöèîíàëüíàÿ ôîðìóëà íàçûâàåòñÿ
íåîáùåçíà÷èìîé , åñëè ïðè ñóùåñòâóåò èíòåðïðåòàöèÿ, ïðè
êîòîðîé çíà÷åíèå ôîðìóëû ðàâíÿåòñÿ 0.
35 / 38

80. Âûïîëíèìîñòü, îáùåçíà÷èìîñòü,
ïðîòèâîðå÷èâîñòü
Îïðåäåëåíèå. Ïðîïîçèöèîíàëüíàÿ ôîðìóëà íàçûâàåòñÿ
âûïîëíèìîé , åñëè ñóùåñòâóåò òàêàÿ èíòåðïðåòàöèÿ, ïðè
êîòîðîé çíà÷åíèå ôîðìóëû ðàâíÿåòñÿ 1.
Îïðåäåëåíèå. Ïðîïîçèöèîíàëüíàÿ ôîðìóëà íàçûâàåòñÿ
íåâûïîëíèìîé (èëè ïðîòèâîðå÷èâîé) , åñëè ïðè âñåõ
èíòåðïðåòàöèÿõ çíà÷åíèå ôîðìóëû ðàâíÿåòñÿ 0.
Îïðåäåëåíèå. Ïðîïîçèöèîíàëüíàÿ ôîðìóëà íàçûâàåòñÿ
îáùåçíà÷èìîé (èëè òàâòîëîãèåé) , åñëè ïðè âñåõ
èíòåðïðåòàöèÿõ çíà÷åíèå ôîðìóëû ðàâíÿåòñÿ 1.
Îïðåäåëåíèå. Ïðîïîçèöèîíàëüíàÿ ôîðìóëà íàçûâàåòñÿ
íåîáùåçíà÷èìîé , åñëè ïðè ñóùåñòâóåò èíòåðïðåòàöèÿ, ïðè
êîòîðîé çíà÷åíèå ôîðìóëû ðàâíÿåòñÿ 0.
35 / 38

81. Âûïîëíèìîñòü, îáùåçíà÷èìîñòü,
ïðîòèâîðå÷èâîñòü
Îïðåäåëåíèå. Ïðîïîçèöèîíàëüíàÿ ôîðìóëà íàçûâàåòñÿ
âûïîëíèìîé , åñëè ñóùåñòâóåò òàêàÿ èíòåðïðåòàöèÿ, ïðè
êîòîðîé çíà÷åíèå ôîðìóëû ðàâíÿåòñÿ 1.
Îïðåäåëåíèå. Ïðîïîçèöèîíàëüíàÿ ôîðìóëà íàçûâàåòñÿ
íåâûïîëíèìîé (èëè ïðîòèâîðå÷èâîé) , åñëè ïðè âñåõ
èíòåðïðåòàöèÿõ çíà÷åíèå ôîðìóëû ðàâíÿåòñÿ 0.
Îïðåäåëåíèå. Ïðîïîçèöèîíàëüíàÿ ôîðìóëà íàçûâàåòñÿ
îáùåçíà÷èìîé (èëè òàâòîëîãèåé) , åñëè ïðè âñåõ
èíòåðïðåòàöèÿõ çíà÷åíèå ôîðìóëû ðàâíÿåòñÿ 1.
Îïðåäåëåíèå. Ïðîïîçèöèîíàëüíàÿ ôîðìóëà íàçûâàåòñÿ
íåîáùåçíà÷èìîé , åñëè ïðè ñóùåñòâóåò èíòåðïðåòàöèÿ, ïðè
êîòîðîé çíà÷åíèå ôîðìóëû ðàâíÿåòñÿ 0.
35 / 38

82. Î ñëîæíîñòè...
• Çàäà÷à îïðåäåëåíèÿ ïî ôîðìóëå â ÊÍÔ, âûïîëíèìà ëè
îíà, ÿâëÿåòñÿ ñëîæíîé (NP-òðóäíîé).
• Ïðîâåðèòü ôîðìóëó â ÊÍÔ, ÿâëÿåòñÿ ëè îíà òàâòîëîãèåé,
î÷åíü ïðîñòî. Äîñòàòî÷íî ïðîâåðèòü, ÷òî â êàæäîì
äèçúþíêòå åñòü ïàðà: ïåðåìåííàÿ è åå îòðèöàíèå.
• Çàäà÷à îïðåäåëåíèÿ ïî ôîðìóëå â ÄÍÔ, âûïîëíèìà ëè
îíà, ÿâëÿåòñÿ ïðîñòîé: äîñòàòî÷íî ïðîâåðèòü, åñòü ëè â
íåé êîíúþíêò, â êîòîðûé îäíîâðåìåííî íå âõîäèò
ïåðåìåííàÿ è åå îòðèöàíèå.
• Ïðîâåðèòü ôîðìóëó â ÄÍÔ, ÿâëÿåòñÿ ëè îíà òàâòîëîãèåé,
ñëîæíî (NP-òðóäíî).
36 / 38

83. Î ñëîæíîñòè...
• Çàäà÷à îïðåäåëåíèÿ ïî ôîðìóëå â ÊÍÔ, âûïîëíèìà ëè
îíà, ÿâëÿåòñÿ ñëîæíîé (NP-òðóäíîé).
• Ïðîâåðèòü ôîðìóëó â ÊÍÔ, ÿâëÿåòñÿ ëè îíà òàâòîëîãèåé,
î÷åíü ïðîñòî. Äîñòàòî÷íî ïðîâåðèòü, ÷òî â êàæäîì
äèçúþíêòå åñòü ïàðà: ïåðåìåííàÿ è åå îòðèöàíèå.
• Çàäà÷à îïðåäåëåíèÿ ïî ôîðìóëå â ÄÍÔ, âûïîëíèìà ëè
îíà, ÿâëÿåòñÿ ïðîñòîé: äîñòàòî÷íî ïðîâåðèòü, åñòü ëè â
íåé êîíúþíêò, â êîòîðûé îäíîâðåìåííî íå âõîäèò
ïåðåìåííàÿ è åå îòðèöàíèå.
• Ïðîâåðèòü ôîðìóëó â ÄÍÔ, ÿâëÿåòñÿ ëè îíà òàâòîëîãèåé,
ñëîæíî (NP-òðóäíî).
36 / 38

84. Î ñëîæíîñòè...
• Çàäà÷à îïðåäåëåíèÿ ïî ôîðìóëå â ÊÍÔ, âûïîëíèìà ëè
îíà, ÿâëÿåòñÿ ñëîæíîé (NP-òðóäíîé).
• Ïðîâåðèòü ôîðìóëó â ÊÍÔ, ÿâëÿåòñÿ ëè îíà òàâòîëîãèåé,
î÷åíü ïðîñòî. Äîñòàòî÷íî ïðîâåðèòü, ÷òî â êàæäîì
äèçúþíêòå åñòü ïàðà: ïåðåìåííàÿ è åå îòðèöàíèå.
• Çàäà÷à îïðåäåëåíèÿ ïî ôîðìóëå â ÄÍÔ, âûïîëíèìà ëè
îíà, ÿâëÿåòñÿ ïðîñòîé: äîñòàòî÷íî ïðîâåðèòü, åñòü ëè â
íåé êîíúþíêò, â êîòîðûé îäíîâðåìåííî íå âõîäèò
ïåðåìåííàÿ è åå îòðèöàíèå.
• Ïðîâåðèòü ôîðìóëó â ÄÍÔ, ÿâëÿåòñÿ ëè îíà òàâòîëîãèåé,
ñëîæíî (NP-òðóäíî).
36 / 38

85. Î ñëîæíîñòè...
• Çàäà÷à îïðåäåëåíèÿ ïî ôîðìóëå â ÊÍÔ, âûïîëíèìà ëè
îíà, ÿâëÿåòñÿ ñëîæíîé (NP-òðóäíîé).
• Ïðîâåðèòü ôîðìóëó â ÊÍÔ, ÿâëÿåòñÿ ëè îíà òàâòîëîãèåé,
î÷åíü ïðîñòî. Äîñòàòî÷íî ïðîâåðèòü, ÷òî â êàæäîì
äèçúþíêòå åñòü ïàðà: ïåðåìåííàÿ è åå îòðèöàíèå.
• Çàäà÷à îïðåäåëåíèÿ ïî ôîðìóëå â ÄÍÔ, âûïîëíèìà ëè
îíà, ÿâëÿåòñÿ ïðîñòîé: äîñòàòî÷íî ïðîâåðèòü, åñòü ëè â
íåé êîíúþíêò, â êîòîðûé îäíîâðåìåííî íå âõîäèò
ïåðåìåííàÿ è åå îòðèöàíèå.
• Ïðîâåðèòü ôîðìóëó â ÄÍÔ, ÿâëÿåòñÿ ëè îíà òàâòîëîãèåé,
ñëîæíî (NP-òðóäíî).
36 / 38

86. Ïðèâåäåíèå ôîðìóëû â ÄÍÔ
• Èçáàâëÿåìñÿ îò èìïëèêàöèè: A→B çàìåíÿåì íà ¬A ∨ B .
• Ïî ïðàâèëàì äå Ìîðãàíà ïðîíîñèì îòðèöàíèÿ äî
ïåðåìåííûõ
• Ïîëüçóÿñü äèñòðèáóòèâíîñòüþ A ∧ (C ∨ D) = A ∧ C ∨ A ∧ D
ðàñêðûâàåì ñêîáêè.
• Óïðîùàåì, âûêèäûâàÿ íåâûïîëíèìûå êîíúþíêòû
Ïðèìåð. ((A ∨ C ) → B) ∧ (A ∨ C )
èçáàâëÿåìñÿ îò èìïëèêàöèè: (¬(A ∨ C ) ∨ B) ∧ (A ∨ C )
ïðîíîñèì îòðèöàíèÿ: ((¬A ∧ ¬C ) ∨ B) ∧ (A ∨ C )
ðàñêðûâàåì ñêîáêè:
(¬A ∧ ¬C ∧ A) ∨ (¬A ∧ ¬C ∧ C ) ∨ (B ∧ A) ∨ (B ∧ C )
óïðîùàåì: (B ∧ A) ∨ (B ∧ C )
37 / 38

87. Ïðèâåäåíèå ôîðìóëû â ÄÍÔ
• Èçáàâëÿåìñÿ îò èìïëèêàöèè: A→B çàìåíÿåì íà ¬A ∨ B .
• Ïî ïðàâèëàì äå Ìîðãàíà ïðîíîñèì îòðèöàíèÿ äî
ïåðåìåííûõ
• Ïîëüçóÿñü äèñòðèáóòèâíîñòüþ A ∧ (C ∨ D) = A ∧ C ∨ A ∧ D
ðàñêðûâàåì ñêîáêè.
• Óïðîùàåì, âûêèäûâàÿ íåâûïîëíèìûå êîíúþíêòû
Ïðèìåð. ((A ∨ C ) → B) ∧ (A ∨ C )
èçáàâëÿåìñÿ îò èìïëèêàöèè: (¬(A ∨ C ) ∨ B) ∧ (A ∨ C )
ïðîíîñèì îòðèöàíèÿ: ((¬A ∧ ¬C ) ∨ B) ∧ (A ∨ C )
ðàñêðûâàåì ñêîáêè:
(¬A ∧ ¬C ∧ A) ∨ (¬A ∧ ¬C ∧ C ) ∨ (B ∧ A) ∨ (B ∧ C )
óïðîùàåì: (B ∧ A) ∨ (B ∧ C )
37 / 38

88. Ïðèâåäåíèå ôîðìóëû â ÄÍÔ
• Èçáàâëÿåìñÿ îò èìïëèêàöèè: A→B çàìåíÿåì íà ¬A ∨ B .
• Ïî ïðàâèëàì äå Ìîðãàíà ïðîíîñèì îòðèöàíèÿ äî
ïåðåìåííûõ
• Ïîëüçóÿñü äèñòðèáóòèâíîñòüþ A ∧ (C ∨ D) = A ∧ C ∨ A ∧ D
ðàñêðûâàåì ñêîáêè.
• Óïðîùàåì, âûêèäûâàÿ íåâûïîëíèìûå êîíúþíêòû
Ïðèìåð. ((A ∨ C ) → B) ∧ (A ∨ C )
èçáàâëÿåìñÿ îò èìïëèêàöèè: (¬(A ∨ C ) ∨ B) ∧ (A ∨ C )
ïðîíîñèì îòðèöàíèÿ: ((¬A ∧ ¬C ) ∨ B) ∧ (A ∨ C )
ðàñêðûâàåì ñêîáêè:
(¬A ∧ ¬C ∧ A) ∨ (¬A ∧ ¬C ∧ C ) ∨ (B ∧ A) ∨ (B ∧ C )
óïðîùàåì: (B ∧ A) ∨ (B ∧ C )
37 / 38

89. Ïðèâåäåíèå ôîðìóëû â ÄÍÔ
• Èçáàâëÿåìñÿ îò èìïëèêàöèè: A→B çàìåíÿåì íà ¬A ∨ B .
• Ïî ïðàâèëàì äå Ìîðãàíà ïðîíîñèì îòðèöàíèÿ äî
ïåðåìåííûõ
• Ïîëüçóÿñü äèñòðèáóòèâíîñòüþ A ∧ (C ∨ D) = A ∧ C ∨ A ∧ D
ðàñêðûâàåì ñêîáêè.
• Óïðîùàåì, âûêèäûâàÿ íåâûïîëíèìûå êîíúþíêòû
Ïðèìåð. ((A ∨ C ) → B) ∧ (A ∨ C )
èçáàâëÿåìñÿ îò èìïëèêàöèè: (¬(A ∨ C ) ∨ B) ∧ (A ∨ C )
ïðîíîñèì îòðèöàíèÿ: ((¬A ∧ ¬C ) ∨ B) ∧ (A ∨ C )
ðàñêðûâàåì ñêîáêè:
(¬A ∧ ¬C ∧ A) ∨ (¬A ∧ ¬C ∧ C ) ∨ (B ∧ A) ∨ (B ∧ C )
óïðîùàåì: (B ∧ A) ∨ (B ∧ C )
37 / 38

90. Ïðèâåäåíèå ôîðìóëû â ÄÍÔ
• Èçáàâëÿåìñÿ îò èìïëèêàöèè: A→B çàìåíÿåì íà ¬A ∨ B .
• Ïî ïðàâèëàì äå Ìîðãàíà ïðîíîñèì îòðèöàíèÿ äî
ïåðåìåííûõ
• Ïîëüçóÿñü äèñòðèáóòèâíîñòüþ A ∧ (C ∨ D) = A ∧ C ∨ A ∧ D
ðàñêðûâàåì ñêîáêè.
• Óïðîùàåì, âûêèäûâàÿ íåâûïîëíèìûå êîíúþíêòû
Ïðèìåð. ((A ∨ C ) → B) ∧ (A ∨ C )
èçáàâëÿåìñÿ îò èìïëèêàöèè: (¬(A ∨ C ) ∨ B) ∧ (A ∨ C )
ïðîíîñèì îòðèöàíèÿ: ((¬A ∧ ¬C ) ∨ B) ∧ (A ∨ C )
ðàñêðûâàåì ñêîáêè:
(¬A ∧ ¬C ∧ A) ∨ (¬A ∧ ¬C ∧ C ) ∨ (B ∧ A) ∨ (B ∧ C )
óïðîùàåì: (B ∧ A) ∨ (B ∧ C )
37 / 38

91. Óïðàæíåíèÿ è çàäà÷è
1 Ïîñòðîéòå ìàøèíó Òüþðèíãà, êîòîðàÿ ïðèáàâëÿåò 1 ê
íàïèñàííîìó äâîè÷íîìó ÷èñëó.
2 Ïîñòðîéòå ìàøèíó Òüþðèíãà, êîòîðàÿ ïðîâåðèò, ÿâëÿåòñÿ
ëè ñòðîêà ïàëèíäðîìîì.
3 Äîêàæèòå, ÷òî íåò àëãîðèòìà, êîòîðûé îïðåäåëÿë áû,
çàêîí÷èò ëè ÌÒ ðàáîòó íà ïóñòîì âõîäå.
4 Ñóùåñòâóåò ëè àëãîðèòì, ïðîâåðÿþùèé, ðàáîòàåò ëè
äàííàÿ ÌÒ ïîëèíîìèàëüíîå âðåìÿ èëè íåò?
5 Äîêàæèòå, ÷òî íå ñóùåñòâóåò àëãîðèòìà, êîòîðûé
îïðåäåëèë áû ïî ÌÒ M îïðåäåëèë áû, ÿâëÿåòñÿ ëè
ïîñëåäîâàòåëüíîñòü M(1), M(2), M(3) . . . ïåðèîäè÷åñêîé ñ
íåêîòîðîãî ìåñòà.
38 / 38