Download to read offline
Uploaded byComputer Science Club
20080323 efficientalgorithms kulikov_lecture19
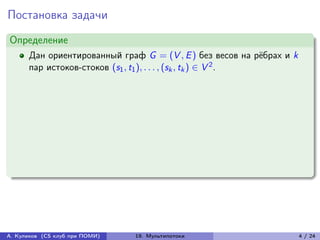
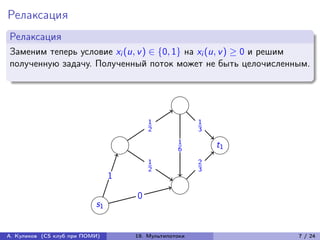
Лекция рассматривает задачу о потоках в сети с несколькими веществами, охватывая постановку задачи, алгоритмы, а также анализ их оптимальности. Основная цель состоит в нахождении множества путей для пар истоков-стоков с минимизацией максимальной ширины рёбер. Лекция также затрагивает методы линейного программирования и переход к целочисленным потокам.
20080323 efficientalgorithms kulikov_lecture19
- 1. с/к “Эффективные алгоритмы” Лекция 19: Потоки в сетях с несколькими веществами А. Куликов Computer Science клуб при ПОМИ http://logic.pdmi.ras.ru/∼infclub/ А. Куликов (CS клуб при ПОМИ) 19. Мультипотоки 1 / 24
- 2. План лекции 1 Постановка задачи А. Куликов (CS клуб при ПОМИ) 19. Мультипотоки 2 / 24
- 3. План лекции 1 Постановка задачи 2 Алгоритм А. Куликов (CS клуб при ПОМИ) 19. Мультипотоки 2 / 24
- 4. План лекции 1 Постановка задачи 2 Алгоритм 3 Анализ алгоритма Оценки Чернова Оценка оптимальности А. Куликов (CS клуб при ПОМИ) 19. Мультипотоки 2 / 24
- 5. План лекции 1 Постановка задачи 2 Алгоритм 3 Анализ алгоритма Оценки Чернова Оценка оптимальности А. Куликов (CS клуб при ПОМИ) 19. Мультипотоки 3 / 24
- 6. Постановка задачи Определение А. Куликов(CS клуб при ПОМИ) 19. Мультипотоки 4 / 24
- 7. Постановка задачи Определение Дан ориентированный граф G = (V , E ) без весов на рёбрах и k пар истоков-стоков (s1 , t1 ), . . . , (sk , tk ) ∈ V 2 . А. Куликов (CS клуб при ПОМИ) 19. Мультипотоки 4 / 24
- 8. Постановка задачи Определение Дан ориентированный граф G = (V , E ) без весов на рёбрах и k пар истоков-стоков (s1 , t1 ), . . . , (sk , tk ) ∈ V 2 . Задача о потоке в сети с несколькими веществами (multicommodity flow problem) заключается в нахождении такого множества путей Pi из si в ti для всех i = 1, . . . , k, при котором максимальная ширина (congestion) рёбер была бы минимальна, где под шириной понимается количество путей, проходящих через это ребро: c(e) = |{Pi | e ∈ Pi }|. А. Куликов (CS клуб при ПОМИ) 19. Мультипотоки 4 / 24
- 9. Постановка задачи Определение Дан ориентированный граф G = (V , E ) без весов на рёбрах и k пар истоков-стоков (s1 , t1 ), . . . , (sk , tk ) ∈ V 2 . Задача о потоке в сети с несколькими веществами (multicommodity flow problem) заключается в нахождении такого множества путей Pi из si в ti для всех i = 1, . . . , k, при котором максимальная ширина (congestion) рёбер была бы минимальна, где под шириной понимается количество путей, проходящих через это ребро: c(e) = |{Pi | e ∈ Pi }|. Факт Задача является NP-трудной. А. Куликов (CS клуб при ПОМИ) 19. Мультипотоки 4 / 24
- 10. План лекции 1 Постановка задачи 2 Алгоритм 3 Анализ алгоритма Оценки Чернова Оценка оптимальности А. Куликов (CS клуб при ПОМИ) 19. Мультипотоки 5 / 24
- 11. Формулировка в видезадачи линейного программирования Формулировка в виде задачи линейного программирования Минимизировать WLP при следующих ограничениях: А. Куликов (CS клуб при ПОМИ) 19. Мультипотоки 6 / 24
- 12. Формулировка в видезадачи линейного программирования Формулировка в виде задачи линейного программирования Минимизировать WLP при следующих ограничениях: 1 Переменные xi (u, v ) определяют поток: ∀v ∈ V , ∀i = 1, . . . , k, ⎧ ∑︁ ∑︁ ⎪1, ⎨ v = si , xi (v , w )− xi (u, v ) = −1, v = ti , ⎪ w : (v ,w )∈E u : (u,v )∈E ⎩ 0, в противном случае. А. Куликов (CS клуб при ПОМИ) 19. Мультипотоки 6 / 24
- 13. Формулировка в видезадачи линейного программирования Формулировка в виде задачи линейного программирования Минимизировать WLP при следующих ограничениях: 1 Переменные xi (u, v ) определяют поток: ∀v ∈ V , ∀i = 1, . . . , k, ⎧ ∑︁ ∑︁ ⎪1, ⎨ v = si , xi (v , w )− xi (u, v ) = −1, v = ti , ⎪ w : (v ,w )∈E u : (u,v )∈E ⎩ 0, в противном случае. 2 Ширина каждого ребра ограничена числом WLP : ∑︀ ∀(u, v ) ∈ E , 1≤i≤k xi (u, v ) ≤ WLP . А. Куликов (CS клуб при ПОМИ) 19. Мультипотоки 6 / 24
- 14. Формулировка в видезадачи линейного программирования Формулировка в виде задачи линейного программирования Минимизировать WLP при следующих ограничениях: 1 Переменные xi (u, v ) определяют поток: ∀v ∈ V , ∀i = 1, . . . , k, ⎧ ∑︁ ∑︁ ⎪1, ⎨ v = si , xi (v , w )− xi (u, v ) = −1, v = ti , ⎪ w : (v ,w )∈E u : (u,v )∈E ⎩ 0, в противном случае. 2 Ширина каждого ребра ограничена числом WLP : ∑︀ ∀(u, v ) ∈ E , 1≤i≤k xi (u, v ) ≤ WLP . 3 Поток является 0 − 1 потоком: ∀(u, v ) ∈ E , ∀i = 1, . . . , k, xi (u, v ) ∈ {0, 1}. А. Куликов (CS клуб при ПОМИ) 19. Мультипотоки 6 / 24
- 15. Релаксация Релаксация Заменим теперь условиеxi (u, v ) ∈ {0, 1} на xi (u, v ) ≥ 0 и решим полученную задачу. Полученный поток может не быть целочисленным. А. Куликов (CS клуб при ПОМИ) 19. Мультипотоки 7 / 24
- 16. Релаксация Релаксация Заменим теперь условиеxi (u, v ) ∈ {0, 1} на xi (u, v ) ≥ 0 и решим полученную задачу. Полученный поток может не быть целочисленным. 1 1 2 3 1 t1 6 1 2 2 3 1 0 s1 А. Куликов (CS клуб при ПОМИ) 19. Мультипотоки 7 / 24
- 17. Переход к целочисленномупотоку Переход к целочисленному потоку А. Куликов (CS клуб при ПОМИ) 19. Мультипотоки 8 / 24
- 18. Переход к целочисленномупотоку Переход к целочисленному потоку Будем обрабатывать каждый из k потоков отдельно. А. Куликов (CS клуб при ПОМИ) 19. Мультипотоки 8 / 24
- 19. Переход к целочисленномупотоку Переход к целочисленному потоку Будем обрабатывать каждый из k потоков отдельно. Рассмотрим граф Gi , содержащий только рёбра, по которым идёт i-й поток. А. Куликов (CS клуб при ПОМИ) 19. Мультипотоки 8 / 24
- 20. Переход к целочисленномупотоку Переход к целочисленному потоку Будем обрабатывать каждый из k потоков отдельно. Рассмотрим граф Gi , содержащий только рёбра, по которым идёт i-й поток. Рассмотрим теперь путь Pi1 в графе Gi из si в ti и пусть i1 = min xi (v , w ). (v ,w )∈P1 А. Куликов (CS клуб при ПОМИ) 19. Мультипотоки 8 / 24
- 21. Переход к целочисленномупотоку Переход к целочисленному потоку Будем обрабатывать каждый из k потоков отдельно. Рассмотрим граф Gi , содержащий только рёбра, по которым идёт i-й поток. Рассмотрим теперь путь Pi1 в графе Gi из si в ti и пусть i1 = min xi (v , w ). (v ,w )∈P1 Вычтем i1 из всех рёбер данного пути: {︃ x(v , w ) − i1 , (v , w ) ∈ Pi1 , x ′ (v , w ) = x(v , w ), в противном случае, найдем новый путь и т.д. А. Куликов (CS клуб при ПОМИ) 19. Мультипотоки 8 / 24
- 22. Переход к целочисленномупотоку Переход к целочисленному потоку Будем обрабатывать каждый из k потоков отдельно. Рассмотрим граф Gi , содержащий только рёбра, по которым идёт i-й поток. Рассмотрим теперь путь Pi1 в графе Gi из si в ti и пусть i1 = min xi (v , w ). (v ,w )∈P1 Вычтем i1 из всех рёбер данного пути: {︃ x(v , w ) − i1 , (v , w ) ∈ Pi1 , x ′ (v , w ) = x(v , w ), в противном случае, найдем новый путь и т.д. На каждом шаге хотя бы одно ребро удаляется из Gi . А. Куликов (CS клуб при ПОМИ) 19. Мультипотоки 8 / 24
- 23. Переход к целочисленномупотоку Переход к целочисленному потоку А. Куликов (CS клуб при ПОМИ) 19. Мультипотоки 9 / 24
- 24. Переход к целочисленномупотоку Переход к целочисленному потоку В итоге, поток i-го вещества разбивается на ji путей Pi1 , . . . , Piji из si в ti , где вдоль пути Pij идёт ij вещества, так что ∑︁ ∀(u, v ) ∈ E , ∀i = 1, . . . , k, ij = xi (u, v ), j:(u,v )∈Pij ji ∑︁ ∀i = 1, . . . , k, ij = 1. j=1 А. Куликов (CS клуб при ПОМИ) 19. Мультипотоки 9 / 24
- 25. Переход к целочисленномупотоку Переход к целочисленному потоку В итоге, поток i-го вещества разбивается на ji путей Pi1 , . . . , Piji из si в ti , где вдоль пути Pij идёт ij вещества, так что ∑︁ ∀(u, v ) ∈ E , ∀i = 1, . . . , k, ij = xi (u, v ), j:(u,v )∈Pij ji ∑︁ ∀i = 1, . . . , k, ij = 1. j=1 В качестве пути Pi из si в ti алгоритм выбирает путь Pij с вероятностью ij . А. Куликов (CS клуб при ПОМИ) 19. Мультипотоки 9 / 24
- 26. Общая схема алгоритма Общаясхема алгоритма А. Куликов (CS клуб при ПОМИ) 19. Мультипотоки 10 / 24
- 27. Общая схема алгоритма Общаясхема алгоритма Решить релаксированную задачу линейного программирования, получив минимальную ширину WLP . А. Куликов (CS клуб при ПОМИ) 19. Мультипотоки 10 / 24
- 28. Общая схема алгоритма Общаясхема алгоритма Решить релаксированную задачу линейного программирования, получив минимальную ширину WLP . Разбить полученные потоки на пути Pij для i = 1, . . . , k, j = 1, . . . , ji (где Pij — путь из s∑︀ ti ), поток по каждому из i в которых равен ij > 0, так что j ij = 1 и ∑︁ ∑︁ ≤ WLP . i j : (v ,w )∈Pi ,j А. Куликов (CS клуб при ПОМИ) 19. Мультипотоки 10 / 24
- 29. Общая схема алгоритма Общаясхема алгоритма Решить релаксированную задачу линейного программирования, получив минимальную ширину WLP . Разбить полученные потоки на пути Pij для i = 1, . . . , k, j = 1, . . . , ji (где Pij — путь из s∑︀ ti ), поток по каждому из i в которых равен ij > 0, так что j ij = 1 и ∑︁ ∑︁ ≤ WLP . i j : (v ,w )∈Pi ,j Для каждого i подбросить монетку с ji гранями, где j-ая грань выпадает с вероятностью ij , и при выпадении грани f выбрать в качестве пути из si в ti путь Pif . А. Куликов (CS клуб при ПОМИ) 19. Мультипотоки 10 / 24
- 30. План лекции 1 Постановка задачи 2 Алгоритм 3 Анализ алгоритма Оценки Чернова Оценка оптимальности А. Куликов (CS клуб при ПОМИ) 19. Мультипотоки 11 / 24
- 31. План лекции 1 Постановка задачи 2 Алгоритм 3 Анализ алгоритма Оценки Чернова Оценка оптимальности А. Куликов (CS клуб при ПОМИ) 19. Мультипотоки 12 / 24
- 32. Оценки Чернова Теорема Пусть Xiсуть независимые случайные переменные, принимаюащие значение 1 с вероятностью pi и значение 0 с вероятностью (1 − pi ). Тогда для всех > 0 и t > 0 (︃ k )︃ k k ∑︁ ∏︁ (︁ )︁ ∏︁ Prob Xi > t ≤ e −t E e Xi = e −t (pi e + (1 − pi )) . i=1 i=1 i=1 А. Куликов (CS клуб при ПОМИ) 19. Мультипотоки 13 / 24
- 33. Оценки Чернова Теорема Пусть Xiсуть независимые случайные переменные, принимаюащие значение 1 с вероятностью pi и значение 0 с вероятностью (1 − pi ). Тогда для всех > 0 и t > 0 (︃ k )︃ k k ∑︁ ∏︁ (︁ )︁ ∏︁ Prob Xi > t ≤ e −t E e Xi = e −t (pi e + (1 − pi )) . i=1 i=1 i=1 Доказательство (︃ k )︃ ∑︁ (︁ ∑︀k )︁ Prob Xi > t = Prob e i =1 Xi > e t . i=1 А. Куликов (CS клуб при ПОМИ) 19. Мультипотоки 13 / 24
- 34. Доказательство (завершение) Доказательство Неравенство Маркова:для любой неотрицательной случайной величины Y E (Y ) Prob (Y > a) ≤ . a А. Куликов (CS клуб при ПОМИ) 19. Мультипотоки 14 / 24
- 35. Доказательство (завершение) Доказательство Неравенство Маркова:для любой неотрицательной случайной величины Y E (Y ) Prob (Y > a) ≤ . a Таким образом, (︃ k )︃ k ∑︁ (︁ ∑︀k )︁ ∏︁ (︁ )︁ Prob Xi > t ≤ e −t E e i =1 Xi = e −t E e Xi . i=1 i=1 А. Куликов (CS клуб при ПОМИ) 19. Мультипотоки 14 / 24
- 36. Следствие Следствие (︁∑︀ )︁ k ∑︀k Пусть M = E i=1 Xi = i=1 pi . Тогда для любого > 0 k (︃ )︃ ∑︁ ∏︀k ≤ (1 + )−(1+)M (1 + )Xi (︀ )︀ Prob Xi > (1 + )M i=1 E i=1 (︁ )︁M e ≤ (1+)(1+) . А. Куликов (CS клуб при ПОМИ) 19. Мультипотоки 15 / 24
- 37. Следствие Следствие (︁∑︀ )︁ k ∑︀k Пусть M = E i=1 Xi = i=1 pi . Тогда для любого > 0 k (︃ )︃ ∑︁ ∏︀k ≤ (1 + )−(1+)M (1 + )Xi (︀ )︀ Prob Xi > (1 + )M i=1 E i=1 (︁ )︁M e ≤ (1+)(1+) . Доказательство А. Куликов (CS клуб при ПОМИ) 19. Мультипотоки 15 / 24
- 38. Следствие Следствие (︁∑︀ )︁ k ∑︀k Пусть M = E i=1 Xi = i=1 pi . Тогда для любого > 0 k (︃ )︃ ∑︁ ∏︀k ≤ (1 + )−(1+)M (1 + )Xi (︀ )︀ Prob Xi > (1 + )M i=1 E i=1 (︁ )︁M e ≤ (1+)(1+) . Доказательство Первое неравенство следует из только что доказанной теоремы при t = (1 + )M, = ln(1 + ). А. Куликов (CS клуб при ПОМИ) 19. Мультипотоки 15 / 24
- 39. Следствие Следствие (︁∑︀ )︁ k ∑︀k Пусть M = E i=1 Xi = i=1 pi . Тогда для любого > 0 k (︃ )︃ ∑︁ ∏︀k ≤ (1 + )−(1+)M (1 + )Xi (︀ )︀ Prob Xi > (1 + )M i=1 E i=1 (︁ )︁M e ≤ (1+)(1+) . Доказательство Первое неравенство следует из только что доказанной теоремы при t = (1 + )M, = ln(1 + ). Второе — из следующего неравенства: E (1 + )Xi = pi (1 + ) + (1 − pi ) = 1 + pi = 1 + pi ≤ e pi . (︀ )︀ А. Куликов (CS клуб при ПОМИ) 19. Мультипотоки 15 / 24
- 40. План лекции 1 Постановка задачи 2 Алгоритм 3 Анализ алгоритма Оценки Чернова Оценка оптимальности А. Куликов (CS клуб при ПОМИ) 19. Мультипотоки 16 / 24
- 41. Основная теорема Теорема Пусть дано > 0. Если оптимальное решение задачи о потоке в сети с несколькими веществами удовлетворяет неравенству W * ≤ c1 () ln n, где n = |V |, то алгоритм находит решение, удовлетворяющее √ неравенству W ≤ W * + c2 () W * ln n, с вероятностью 1 − (c1 , c2 суть константы, зависящие от ). А. Куликов (CS клуб при ПОМИ) 19. Мультипотоки 17 / 24
- 42. Основная теорема Теорема Пусть дано > 0. Если оптимальное решение задачи о потоке в сети с несколькими веществами удовлетворяет неравенству W * ≤ c1 () ln n, где n = |V |, то алгоритм находит решение, удовлетворяющее √ неравенству W ≤ W * + c2 () W * ln n, с вероятностью 1 − (c1 , c2 суть константы, зависящие от ). Доказательство А. Куликов (CS клуб при ПОМИ) 19. Мультипотоки 17 / 24
- 43. Основная теорема Теорема Пусть дано > 0. Если оптимальное решение задачи о потоке в сети с несколькими веществами удовлетворяет неравенству W * ≤ c1 () ln n, где n = |V |, то алгоритм находит решение, удовлетворяющее √ неравенству W ≤ W * + c2 () W * ln n, с вероятностью 1 − (c1 , c2 суть константы, зависящие от ). Доказательство Зафиксируем ребро (v , w ) ∈ E . А. Куликов (CS клуб при ПОМИ) 19. Мультипотоки 17 / 24
- 44. Основная теорема Теорема Пусть дано > 0. Если оптимальное решение задачи о потоке в сети с несколькими веществами удовлетворяет неравенству W * ≤ c1 () ln n, где n = |V |, то алгоритм находит решение, удовлетворяющее √ неравенству W ≤ W * + c2 () W * ln n, с вероятностью 1 − (c1 , c2 суть константы, зависящие от ). Доказательство Зафиксируем ребро (v , w ) ∈ E . Ребро (v , w ) используется i-м потоком с вероятностью ∑︀ pi = j : (v ,w )∈Pij ij . А. Куликов (CS клуб при ПОМИ) 19. Мультипотоки 17 / 24
- 45. Основная теорема Теорема Пусть дано > 0. Если оптимальное решение задачи о потоке в сети с несколькими веществами удовлетворяет неравенству W * ≤ c1 () ln n, где n = |V |, то алгоритм находит решение, удовлетворяющее √ неравенству W ≤ W * + c2 () W * ln n, с вероятностью 1 − (c1 , c2 суть константы, зависящие от ). Доказательство Зафиксируем ребро (v , w ) ∈ E . Ребро (v , w ) используется i-м потоком с вероятностью ∑︀ pi = j : (v ,w )∈Pij ij . Пусть Xi — случайная 0/1-переменная, принимающая значение 1 с веротяностью pi . А. Куликов (CS клуб при ПОМИ) 19. Мультипотоки 17 / 24
- 46. Основная теорема Теорема Пусть дано > 0. Если оптимальное решение задачи о потоке в сети с несколькими веществами удовлетворяет неравенству W * ≤ c1 () ln n, где n = |V |, то алгоритм находит решение, удовлетворяющее √ неравенству W ≤ W * + c2 () W * ln n, с вероятностью 1 − (c1 , c2 суть константы, зависящие от ). Доказательство Зафиксируем ребро (v , w ) ∈ E . Ребро (v , w ) используется i-м потоком с вероятностью ∑︀ pi = j : (v ,w )∈Pij ij . Пусть Xi — случайная 0/1-переменная, принимающая значение 1 с веротяностью pi . Тогда W (v , w ) = k Xi . ∑︀ i=1 А. Куликов (CS клуб при ПОМИ) 19. Мультипотоки 17 / 24
- 47. Доказательство (продолжение) Доказательство ∑︁ ∑︁ ∑︁ E (W (v , w )) = pi = ij ≤ WLP ≤ W * i i j : (v ,w )∈Pij А. Куликов (CS клуб при ПОМИ) 19. Мультипотоки 18 / 24
- 48. Доказательство (продолжение) Доказательство ∑︁ ∑︁ ∑︁ E (W (v , w )) = pi = ij ≤ WLP ≤ W * i i j : (v ,w )∈Pij )︂W * e (︂ * * Prob (W (v , w ) ≥ (1 + )W ) ≤ = e (−(1+) ln(1+))W (1 + )(1+) А. Куликов (CS клуб при ПОМИ) 19. Мультипотоки 18 / 24
- 49. Доказательство (продолжение) Доказательство ∑︁ ∑︁ ∑︁ E (W (v , w )) = pi = ij ≤ WLP ≤ W * i i j : (v ,w )∈Pij )︂W * e (︂ * * Prob (W (v , w ) ≥ (1 + )W ) ≤ = e (−(1+) ln(1+))W (1 + )(1+) при ≤ 1 выполнено неравенство − (1 + ) ln(1 + ) ≤ − 2 /3 А. Куликов (CS клуб при ПОМИ) 19. Мультипотоки 18 / 24
- 50. Доказательство (продолжение) Доказательство √︂ 2 3 ln n Поэтому при = W* имеем Prob (W (v , w ) ≥ (1 + )W * ) ≤ n2 . А. Куликов (CS клуб при ПОМИ) 19. Мультипотоки 19 / 24
- 51. Доказательство (продолжение) Доказательство √︂ n2 3 ln * Поэтому при = W * имеем Prob (W (v , w ) ≥ (1 + )W ) ≤ . n2 Неравенство ≤ 1 выполнено при W * ≥ 6 ln n − 3 ln . А. Куликов (CS клуб при ПОМИ) 19. Мультипотоки 19 / 24
- 52. Доказательство (продолжение) Доказательство √︂ n2 3 ln * Поэтому при = W * имеем Prob (W (v , w ) ≥ (1 + )W ) ≤ n2 . Неравенство ≤ 1 выполнено при W * ≥ 6 ln n − 3 ln . При таком √︂ * * n2 (1 + )W = W + 3W * ln . Теперь оценим вероятность: (︂ )︂ max W (v , w ) ≥ (1 + )W * ∑︀ Prob ≤ (v ,w )∈E Prob (W (v , w ) ≥ (1 + (v ,w )∈E ≤ |E | n2 ≤ . А. Куликов (CS клуб при ПОМИ) 19. Мультипотоки 19 / 24
- 53. Дерандомизация (основная идея) Дерандомизация(основная идея) А. Куликов (CS клуб при ПОМИ) 19. Мультипотоки 20 / 24
- 54. Дерандомизация (основная идея) Дерандомизация(основная идея) Алгоритм можно дерандомизировать методом условных вероятностей. А. Куликов (CS клуб при ПОМИ) 19. Мультипотоки 20 / 24
- 55. Дерандомизация (основная идея) Дерандомизация(основная идея) Алгоритм можно дерандомизировать методом условных вероятностей. Для каждого вещества нам нужно выбрать один из путей. А. Куликов (CS клуб при ПОМИ) 19. Мультипотоки 20 / 24
- 56. Дерандомизация (основная идея) Дерандомизация(основная идея) Алгоритм можно дерандомизировать методом условных вероятностей. Для каждого вещества нам нужно выбрать один из путей. Рассмотрим дерево высоты k, где у корня есть j1 сыновей, у каждого из них — j2 сыновей и т.д. А. Куликов (CS клуб при ПОМИ) 19. Мультипотоки 20 / 24
- 57. Дерандомизация (основная идея) Дерандомизация(основная идея) Алгоритм можно дерандомизировать методом условных вероятностей. Для каждого вещества нам нужно выбрать один из путей. Рассмотрим дерево высоты k, где у корня есть j1 сыновей, у каждого из них — j2 сыновей и т.д. На i-м уровне, таким образом, принимается решение, какой путь выбрать для i-го потока. А. Куликов (CS клуб при ПОМИ) 19. Мультипотоки 20 / 24
- 58. Дерандомизация (основная идея) Дерандомизация(основная идея) Алгоритм можно дерандомизировать методом условных вероятностей. Для каждого вещества нам нужно выбрать один из путей. Рассмотрим дерево высоты k, где у корня есть j1 сыновей, у каждого из них — j2 сыновей и т.д. На i-м уровне, таким образом, принимается решение, какой путь выбрать для i-го потока. Листья данного дерева представляют допустимые решения нашей задачи. А. Куликов (CS клуб при ПОМИ) 19. Мультипотоки 20 / 24
- 59. Дерандомизация (основная идея) Дерандомизация(основная идея) Определим ⎛ ⃒l для вещества 1 ⎞ ⃒1 ⃒l *⃒ 2 для вещества 2 g (l1 , . . . , li ) = Prob ⎝ max W (v , w ) ≥ (1 + )W ⃒ . . ⎠ (v ,w )∈E ⃒ . li для вещества i А. Куликов (CS клуб при ПОМИ) 19. Мультипотоки 21 / 24
- 60. Дерандомизация (основная идея) Дерандомизация(основная идея) Определим ⎛ ⃒l для вещества 1 ⎞ ⃒1 ⃒l *⃒ 2 для вещества 2 g (l1 , . . . , li ) = Prob ⎝ max W (v , w ) ≥ (1 + )W ⃒ . . ⎠ (v ,w )∈E ⃒ . li для вещества i Ясно, что ji ∑︁ g (l1 , . . . , li−1 ) = ij g (l1 , . . . , li−1 , j) ≥ min g (l1 , . . . , li−1 , j). j j=1 А. Куликов (CS клуб при ПОМИ) 19. Мультипотоки 21 / 24
- 61. Дерандомизация (основная идея) Дерандомизация(основная идея) А. Куликов (CS клуб при ПОМИ) 19. Мультипотоки 22 / 24
- 62. Дерандомизация (основная идея) Дерандомизация(основная идея) Таким образом, если бы мы могли вычислять g (l1 , . . . , li ) эффективно, мы бы начали с g (∅) и, выбирая минимум на каждом шаге, построили бы последовательность g (∅) ≥ g (l1 ) ≥ g (l1 , l2 ) ≥ · · · ≥ g (l1 , . . . , lk ). А. Куликов (CS клуб при ПОМИ) 19. Мультипотоки 22 / 24
- 63. Дерандомизация (основная идея) Дерандомизация(основная идея) Таким образом, если бы мы могли вычислять g (l1 , . . . , li ) эффективно, мы бы начали с g (∅) и, выбирая минимум на каждом шаге, построили бы последовательность g (∅) ≥ g (l1 ) ≥ g (l1 , l2 ) ≥ · · · ≥ g (l1 , . . . , lk ). Однако непонятно, как именно вычислять такие вероятности. А. Куликов (CS клуб при ПОМИ) 19. Мультипотоки 22 / 24
- 64. Дерандомизация (основная идея) Дерандомизация(основная идея) Таким образом, если бы мы могли вычислять g (l1 , . . . , li ) эффективно, мы бы начали с g (∅) и, выбирая минимум на каждом шаге, построили бы последовательность g (∅) ≥ g (l1 ) ≥ g (l1 , l2 ) ≥ · · · ≥ g (l1 , . . . , lk ). Однако непонятно, как именно вычислять такие вероятности. Из оценок Чернова можно вывести некоторую верхнюю оценку h(l1 , . . . , li ) на g (l1 , . . . , li ), вычислить которую легко. А. Куликов (CS клуб при ПОМИ) 19. Мультипотоки 22 / 24
- 65. Дерандомизация (основная идея) Дерандомизация(основная идея) Таким образом, если бы мы могли вычислять g (l1 , . . . , li ) эффективно, мы бы начали с g (∅) и, выбирая минимум на каждом шаге, построили бы последовательность g (∅) ≥ g (l1 ) ≥ g (l1 , l2 ) ≥ · · · ≥ g (l1 , . . . , lk ). Однако непонятно, как именно вычислять такие вероятности. Из оценок Чернова можно вывести некоторую верхнюю оценку h(l1 , . . . , li ) на g (l1 , . . . , li ), вычислить которую легко. После этого выичсляется последовательность 1 > ≥ h(∅) ≥ h(l1 , l2 ) ≥ · · · ≥ h(l1 , . . . , lk ) ≥ g (l1 , . . . , lk ). А. Куликов (CS клуб при ПОМИ) 19. Мультипотоки 22 / 24
- 66. Дерандомизация (основная идея) Дерандомизация(основная идея) Таким образом, если бы мы могли вычислять g (l1 , . . . , li ) эффективно, мы бы начали с g (∅) и, выбирая минимум на каждом шаге, построили бы последовательность g (∅) ≥ g (l1 ) ≥ g (l1 , l2 ) ≥ · · · ≥ g (l1 , . . . , lk ). Однако непонятно, как именно вычислять такие вероятности. Из оценок Чернова можно вывести некоторую верхнюю оценку h(l1 , . . . , li ) на g (l1 , . . . , li ), вычислить которую легко. После этого выичсляется последовательность 1 > ≥ h(∅) ≥ h(l1 , l2 ) ≥ · · · ≥ h(l1 , . . . , lk ) ≥ g (l1 , . . . , lk ). Иэ этого следует, что g (l1 , . . . , lk ) = 0. А. Куликов (CS клуб при ПОМИ) 19. Мультипотоки 22 / 24
- 67. Что мы узнализа сегодня? Что мы узнали за сегодня? А. Куликов (CS клуб при ПОМИ) 19. Мультипотоки 23 / 24
- 68. Что мы узнализа сегодня? Что мы узнали за сегодня? Задача о потоке в сети с несколькими веществами NP-трудна. А. Куликов (CS клуб при ПОМИ) 19. Мультипотоки 23 / 24
- 69. Что мы узнализа сегодня? Что мы узнали за сегодня? Задача о потоке в сети с несколькими веществами NP-трудна. Может быть решена приближенно релаксацией целочисленной задачи линейного программирования с последующим случайным выбором путей. А. Куликов (CS клуб при ПОМИ) 19. Мультипотоки 23 / 24
- 70. Что мы узнализа сегодня? Что мы узнали за сегодня? Задача о потоке в сети с несколькими веществами NP-трудна. Может быть решена приближенно релаксацией целочисленной задачи линейного программирования с последующим случайным выбором путей. Алгоритм можно дерандомизировать методом условных вероятностей. А. Куликов (CS клуб при ПОМИ) 19. Мультипотоки 23 / 24
- 71. Спасибо за внимание! А.Куликов (CS клуб при ПОМИ) 19. Мультипотоки 24 / 24