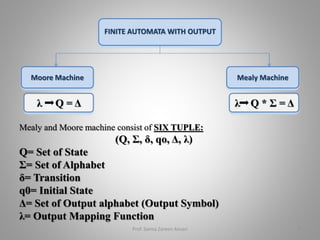
This document outlines the syllabus for a course on formal languages and automata theory. The syllabus covers six units: (1) mathematical preliminaries, (2) finite automata and regular languages, (3) regular expressions and grammars, (4) context-free languages and pushdown automata, (5) Turing machines and variations, and (6) recursively enumerable and recursive sets. It also lists six course outcomes related to classifying languages and automata, formal relationships among models of computation, constructing grammars and automata, and demonstrating concepts in computability and decidability. The document provides examples and definitions for Moore and Mealy machines, and procedures for converting between the two models.

1. 1
Prof. Saima Zareen Ansari

2. Syllabus:
 Unit 1: Mathematical preliminaries –Sets, operations,
relations, strings, closure of relation, countability and
diagonalization, induction and proof methods- pigeon-hole
principle ,concept of language, formal grammars, Chomsky
hierarchy.
 Unit 2: Finite Automaton, regular languages, deterministic &
non deterministic finite automata, ϵ-closures, minimization of
automata, equivalence, Moore and Mealy machine.
 Unit 3: Regular expression, identities, Regular grammar, right
linear, left linear, Arden theorem, Pumping lemma for regular
sets, closure & decision properties for regular sets, Context
free languages, parse trees and ambiguity, reduction of CFGS,
Normal forms for CFG .
Prof. Saima Zareen Ansari

3.  Unit 4: Push down Automata (PDA), non-determinism,
acceptance by two methods and their equivalence, conversion
of PDA to CFG, CFG to PDAs, closure and decision
properties of CFLs, pumping lemma for CFL.
 Unit 5: Turing machines, TM as acceptor, TM as
transducers, Variations of TM, linear bounded automata, TM
as computer of function.
 Unit 6: Recursively enumerable (r.e.) set, recursive sets,
Decidability and solvability, Post correspondence Problem
(PCP), Introduction to recursive function theory, primitive
recursive functions, Ackerman function.
3
Prof. Saima Zareen Ansari

4. COURSE OUTCOMES:
 CO1: Classify the concept of languages and automata.
 CO2: Explain the formal relationships among machines,
languages and grammars.
 CO3: Construct Regular Grammar and normal forms for CFG.
 CO4: Design and develop finite automata for given regular
language.
 CO5: Design Push Down Automata, Turing Machine for given
languages
 CO6: Demonstrate use of computability, decidability, recursive
function theory through problem solving
4
Prof. Saima Zareen Ansari

5. 5
Prof. Saima Zareen Ansari

6. FINITE AUTOMATA
FINITE AUTOMATA WITHOUT
OUTPUT
FINITE AUTOMATA WITH OUTPUT
Moore Machine
Mealy Machine
NFA with ϵ
DFA NFA
6
Prof. Saima Zareen Ansari

7. FINITE AUTOMATA WITH OUTPUT
Moore Machine Mealy Machine
Mealy and Moore machine consist of SIX TUPLE:
(Q, Ʃ, δ, qo, Δ, λ)
Q= Set of State
Ʃ= Set of Alphabet
δ= Transition
q0= Initial State
Δ= Set of Output alphabet (Output Symbol)
λ= Output Mapping Function
λ Q * Ʃ = Δ
λ Q = Δ
0 0
7
Prof. Saima Zareen Ansari

8. ConversionofMealyMachinetoMooreMachine
1. Find out different output generated with qί in the
next state column of Mealy Machine.
2. Then split qί into different states depending upon
output generated with it.
For example: If output generated by qί is ‘1’ in
the first next state column & ‘0’ in the second next
state column, then split q1 into q10 & q11.
Follow the above steps for all the states.
3. Now copy all the present states & next states in
Moore machine format and output of the next
state are common. 8
Prof. Saima Zareen Ansari

9. ConversionofMealytoMooreMachine
Q * Ʃ = Δ : Q = Δ
9
Prof. Saima Zareen Ansari

10. Conversionof MooreMachinetoMealyMachine
1. Draw the Mealy machine table.
2. Copy all the Present state & Next state column of
the states into the table.
3. For output column of the Next state, check Present
state & its output generated in the Moore Machine
table.
For example: If output generated by state Qί is
‘m’, copy this output into the output column of
Mealy machine table wherever Qί is present in the
next state.
10
Prof. Saima Zareen Ansari

11. Conversionof MooretoMealyMachine
Q = Δ : Q * Ʃ = Δ
11
Prof. Saima Zareen Ansari

12. Constructionof Moore & MelayMachine
12
Prof. Saima Zareen Ansari

13. 13
Prof. Saima Zareen Ansari