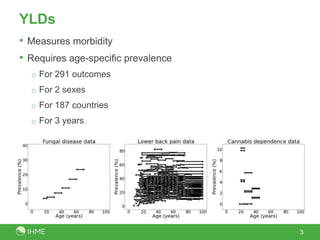
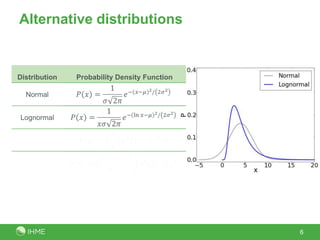
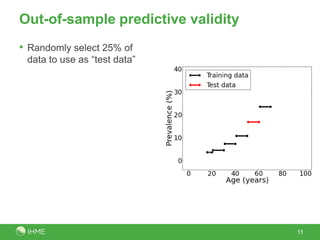
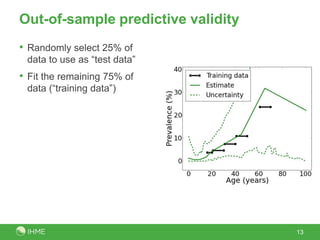
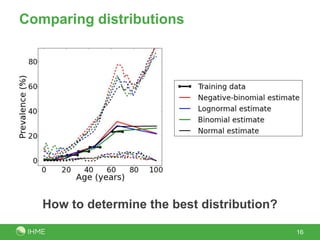
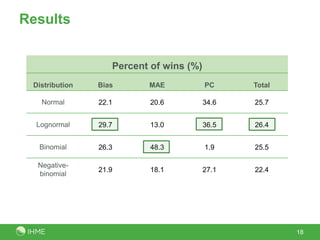
The document discusses the robustness of the meta-regression model using dismod-mr, focusing on the choice of distribution for data analysis in the Global Burden of Disease Study 2010. It evaluates the performance of various distributions (normal, lognormal, binomial, negative-binomial) through out-of-sample predictive validity and concludes that the lognormal distribution typically performs best, although the choice of distribution has minimal impact on results. Further investigation is suggested to determine optimal conditions for different distributions based on covariates and data volume.

1. Meta-regression with DisMod-MR:
how robust is the model?
June 18, 2013
Hannah M Peterson
Post-Bachelor Fellow

2. Global Burden of Disease Study 2010
2

3. YLDs
• Measures morbidity
• Requires age-specific prevalence
o For 291 outcomes
o For 2 sexes
o For 187 countries
o For 3 years
3

4. Is negative-binomial distribution
the best choice?
DisMod-MR
4

5. Alternative distributions
5
Distribution Probability Density Function
Normal
Lognormal
Binomial
Negative-
binomial

6. Alternative distributions
6
Distribution Probability Density Function
Normal
Lognormal
Binomial
Negative-
binomial

7. Alternative distributions
7
Distribution Probability Density Function
Normal
Lognormal
Binomial
Negative-
binomial

8. Alternative distributions
8
Distribution Probability Density Function
Normal
Lognormal
Binomial
Negative-
binomial

9. Potential experimental frameworks
• Data collection
o Ideal
o Impractical
• Simulation
o Impossible to know true data distribution
• Out-of-sample cross validation
o Do not have to choose distribution
9

10. Out-of-sample cross validation
10

11. Out-of-sample predictive validity
• Randomly select 25% of
data to use as “test data”
11

12. Out-of-sample predictive validity
• Randomly select 25% of
data to use as “test data”
12

13. Out-of-sample predictive validity
• Randomly select 25% of
data to use as “test data”
• Fit the remaining 75% of
data (“training data”)
13

14. Out-of-sample predictive validity
• Randomly select 25% of
data to use as “test data”
• Fit the remaining 75% of
data (“training data”)
• Use fit to calculate statistics
for test data
14

15. Out-of-sample predictive validity
• Randomly select 25% of
data to use as “test data”
• Fit the remaining 75% of
data (“training data”)
• Use fit to calculate statistics
for test data
• For each distribution
• For 1000 test-train splits
• For each disease data set
15

16. Comparing distributions
16
How to determine the best distribution?

17. Metrics of evaluation
•
17

18. Results
18
Percent of wins (%)
Distribution Bias MAE PC Total
Normal 22.1 20.6 34.6 25.7
Lognormal 29.7 13.0 36.5 26.4
Binomial 26.3 48.3 1.9 25.5
Negative-
binomial
21.9 18.1 27.1 22.4

19. Conclusions
• Choice of distribution doesn’t greatly influence results
• Best overall performance: lognormal distribution
o Contingent on method to adjust data whose value is 0
• Further investigate when each distribution performs best
o Dependent on number of covariates, priors, amount of data?
19

20. Thank you
Hannah Peterson
peterhm@uw.edu
www.healthmetricsandevaluation.org