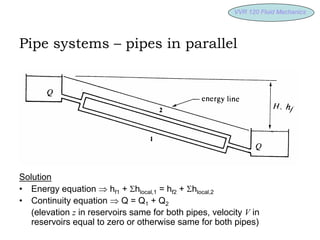
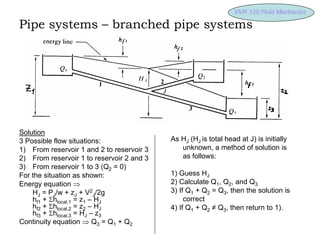
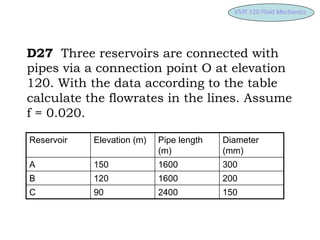
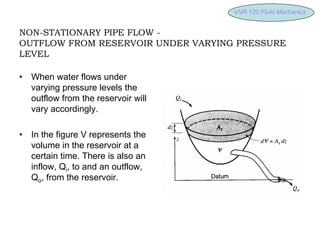
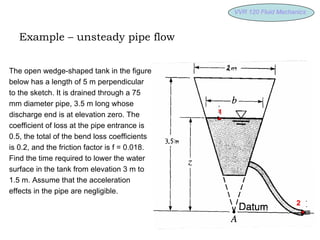
This document discusses pipe flow and fluid mechanics concepts including: 1) Pipes connected in parallel and calculating flow rates using the continuity and energy equations. 2) Branched pipe systems with three reservoirs and calculating unknown flow rates by guessing the total head and applying the continuity and energy equations. 3) Non-stationary pipe flow where the outflow from a reservoir varies with changing pressure levels over time according to integration of the continuity equation.

1. VVR 120 Fluid
VVR 120 Fluid Mechanics
Mechanics
14. Pipe flow II (6.4, 7.1-7.4)
• Pipes in parallel
• Three reservoir problem
• Quasi stationary pipe flow
Exercises: D21, D26, and (D27)

2. VVR 120 Fluid
VVR 120 Fluid Mechanics
Mechanics
Pipe systems – pipes in parallel
Solution
• Energy equation ⇒ hf1 + Σhlocal,1 = hf2 + Σhlocal,2
• Continuity equation ⇒ Q = Q1 + Q2
(elevation z in reservoirs same for both pipes, velocity V in
reservoirs equal to zero or otherwise same for both pipes)

3. VVR 120 Fluid
VVR 120 Fluid Mechanics
Mechanics
D21 A 0.6 m pipeline branches into a 0.3 m and a
0.45 m pipe, each of which is 1.6 km long, and
they rejoin to form a 0.45 m pipe. If 0.85 m3/s
flow in the main pipe, how will the flow divide?
Assume that f = 0.018 for both branches.

4. VVR 120 Fluid
VVR 120 Fluid Mechanics
Mechanics
Example – parallel pipes. A 300 mm pipeline
1500 m long (f = 0.020) is laid between two
reservoirs having a difference of surface elevation
of 24 m. What is the maximum obtainable flowrate
through this line (with all the valves wide open)?
When this pipe is looped with a 400 mm pipe 600
m long (f = 0.025) laid parallel and connected to it,
what increase of maximum flowrate may be
expected? Assume that all local losses may be
neglected.

5. VVR 120 Fluid
VVR 120 Fluid Mechanics
Mechanics
Pipe systems – branched pipe systems
Solution
3 Possible flow situations:
1) From reservoir 1 and 2 to reservoir 3
2) From reservoir 1 to reservoir 2 and 3
3) From reservoir 1 to 3 (Q2 = 0)
For the situation as shown:
Energy equation ⇒
HJ = PJ/w + zJ + V2
J/2g
hf1 + Σhlocal,1 = z1 – HJ
hf2 + Σhlocal,2 = z2 – HJ
hf3 + Σhlocal,3 = HJ – z3
Continuity equation ⇒ Q3 = Q1 + Q2
As HJ (HJ is total head at J) is initially
unknown, a method of solution is
as follows:
1) Guess HJ
2) Calculate Q1, Q2, and Q3
3) If Q1 + Q2 = Q3, then the solution is
correct
4) If Q1 + Q2 ≠ Q3, then return to 1).

6. VVR 120 Fluid
VVR 120 Fluid Mechanics
Mechanics
D26 A 900 mm pipe divides into three 450 mm
pipes at elevation 120. The 450 mm pipes (length,
see table) runs to reservoirs with elevations
according to table. When 1.4 m3/s flows in the big
pipe, how will the flow divide? Assume f = 0.017 in
all pipes.
Reservoir Elevation (m) Pipe length (m)
A 90 3200
B 60 4800
C 30 6800

7. VVR 120 Fluid
VVR 120 Fluid Mechanics
Mechanics
NON-STATIONARY PIPE FLOW -
OUTFLOW FROM RESERVOIR UNDER VARYING PRESSURE
LEVEL
• When water flows under
varying pressure levels the
outflow from the reservoir will
vary accordingly.
• In the figure V represents the
volume in the reservoir at a
certain time. There is also an
inflow, Qi, to and an outflow,
Qo, from the reservoir.

8. VVR 120 Fluid
VVR 120 Fluid Mechanics
Mechanics
NON-STATIONARY PIPE FLOW, cont.
• Volume change in the reservoir during a small time interval dt, can
be expressed as:
dV = (Qi – Qo) · dt and dV = As · dz →
As · dz = (Qi – Qo) · dt where both inflow and outflow can vary in
time.
The outflow can normally be determined by the energy equation that
gives outflow as a function of z. For example outflow through a hole:
Qo = Ahole · CD · (2gz)1/2 (Eqn. 5.12)
If time is to be estimated that changes the water level from z1 to z2
integration of dt = (As /(Qi – Qo)) dz gives:
t = z1∫
z2
(As /(Qi – Qo)) dz this expression can be derivated if Qi = 0 or if Qi
= constant and Qo can be re-written as a function of z. Qo can be
determined by the energy equation during short time periods
assuming stationarity. If water level changes quickly an acceleration
term has to be included though.

9. VVR 120 Fluid
VVR 120 Fluid Mechanics
Mechanics
Example – unsteady pipe flow
The open wedge-shaped tank in the figure
below has a length of 5 m perpendicular
to the sketch. It is drained through a 75
mm diameter pipe, 3.5 m long whose
discharge end is at elevation zero. The
coefficient of loss at the pipe entrance is
0.5, the total of the bend loss coefficients
is 0.2, and the friction factor is f = 0.018.
Find the time required to lower the water
surface in the tank from elevation 3 m to
1.5 m. Assume that the acceleration
effects in the pipe are negligible.
1
1
2
2

10. VVR 120 Fluid
VVR 120 Fluid Mechanics
Mechanics
D27 Three reservoirs are connected with
pipes via a connection point O at elevation
120. With the data according to the table
calculate the flowrates in the lines. Assume
f = 0.020.
Reservoir Elevation (m) Pipe length
(m)
Diameter
(mm)
A 150 1600 300
B 120 1600 200
C 90 2400 150