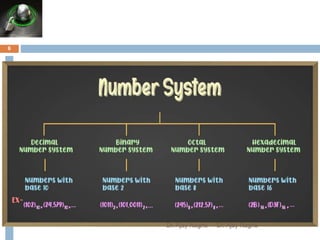
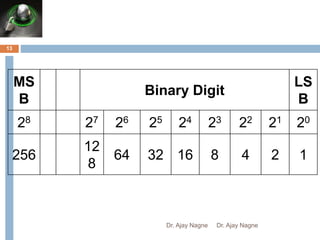
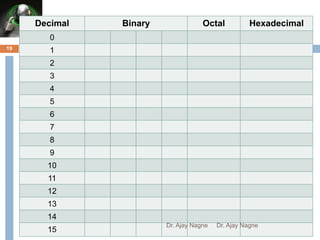
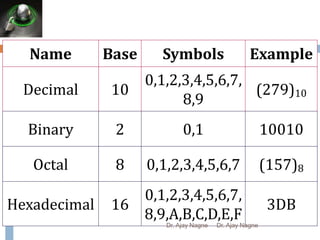
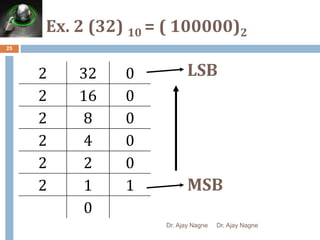
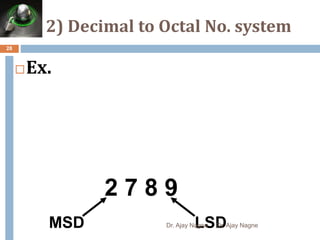
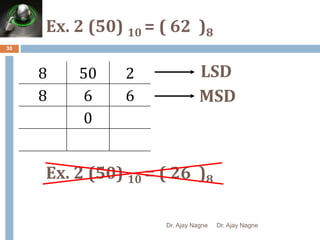
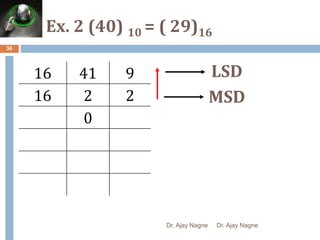
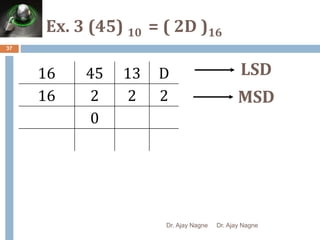
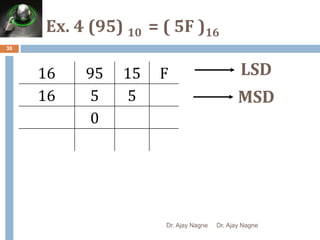
The document discusses different number systems, including decimal, binary, octal, and hexadecimal. It explains that a number system allows numbers to be represented using symbols in a consistent way and defines the base of each system. Conversion between number systems is demonstrated through examples, such as converting the decimal number 32 to the binary number 100000 or converting 95 from decimal to the hexadecimal 5F. Key aspects like most/least significant bits or digits and place values are also outlined.

1. NUMBER SYSTEM
1
Dr. Ajay Nagne
Dr. Ajay Nagne

2. Table of Contents
 What is Number System?
 Types of Number System
 Number System Conversion
2
Dr. Ajay Nagne Dr. Ajay Nagne

3. What is Number System?
3
 A number system is defined as a system of writing
to express numbers.
 It is the mathematical notation for representing
numbers of a given set by using digits or other
symbols in a consistent manner.
 It provides a unique representation of every
number and represents the arithmetic and
algebraic structure of the figures.
 It also allows us to operate arithmetic operations
like addition, subtraction, Multiplication and
division.
Dr. Ajay Nagne Dr. Ajay Nagne

4. The value of any digit in a number
can be determined by:
4
The digit
Its position in the number
The base of the number system
Dr. Ajay Nagne Dr. Ajay Nagne

5. Types of Number System
5
 There are various types of number
system in mathematics. The four most
common number system types are:
Decimal number system (Base- 10)
Binary number system (Base- 2)
Octal number system (Base-8)
Hexadecimal number system (Base- 16)
Dr. Ajay Nagne Dr. Ajay Nagne

6. 6
Dr. Ajay Nagne Dr. Ajay Nagne

7. Decimal Number System (Base 10
Number System)
7
 Decimal number system has base 10
because it uses ten digits from 0 to 9.
 In the decimal number system, the
positions successive to the left of the
decimal point represent units, tens,
hundreds, thousands and so on.
 This system is expressed in decimal
numbers.
Dr. Ajay Nagne Dr. Ajay Nagne

8. Decimal Number System (Base 10
Number System)
8
 Every position shows a particular
power of the base (10).
 For example, the decimal number 1457
consists of the digit 7 in the units
position, 5 in the tens place, 4 in the
hundreds position, and 1 in the
thousands place whose value can be
written as
Dr. Ajay Nagne Dr. Ajay Nagne

9. Decimal Number System (Base 10
Number System)
9
 ( 1 4 5 7 )10 =
= (1×103)
= (1×1000)
= 1000 + 400 + 50 + 7
= 1457
+ (4×102)+ (5×101)+ (7×100)
+ (4×100) + (7×1)
+ (5×10)
Dr. Ajay Nagne Dr. Ajay Nagne

10. 1) Decimal to Binary No. system
10
 Most Significant Digit (MSD )
The Left Most digit having the Highest
weighted Value is Call as MSD.
 Least Significant Digit (LSD)
 The right Most digit having the Lowest
weighted Value is Call as LSD.
 Ex.
2 7 8 9
MSD LSD
Dr. Ajay Nagne Dr. Ajay Nagne

11. Binary Number System (Base 2
Number System)
11
 The base 2 number system is also known
as the Binary number system wherein,
only two binary digits exist, i.e., 0 and 1.
Specifically, the usual base-2 is a radix of
2.
 This system are known as binary numbers
which are the combination of 0 and 1.
 For example, 110101 is a binary number.
Dr. Ajay Nagne Dr. Ajay Nagne

12. Binary Number System
12
bit = 0 or 1
1 Byte = 8 bits
1 Kilobyte = 1024 Byte
1 Megabyte = 1024 Kb
1 Gigabyte= 1024 MB
1 Terabyte = 1024 GB
Dr. Ajay Nagne Dr. Ajay Nagne

13. 13
MS
B
Binary Digit
LS
B
28 27 26 25 24 23 22 21 20
256
12
8
64 32 16 8 4 2 1
Dr. Ajay Nagne Dr. Ajay Nagne

14. Binary Number System
14
Ex.
10010
Dr. Ajay Nagne Dr. Ajay Nagne

15. Binary Number System
15
 Most Significant Bit (MSB )
The Left Most bit having the Highest
weighted Value is Call as MSB.
 Least Significant Bit (LSB)
 The right Most bit having the Lowest
weighted Value is Call as LSB.
 Ex.
10010
MSB LSB
Dr. Ajay Nagne Dr. Ajay Nagne

16. Octal Number System (Base 8
Number System)
16
 In the octal number system, the base is 8 and
it uses numbers from 0 to 7 to represent
numbers.
 Octal numbers are commonly used in
computer applications.
 Converting an octal number to decimal is the
same as decimal conversion and is explained
below using an example.
Dr. Ajay Nagne Dr. Ajay Nagne

17. Hexadecimal Number System
(Base 16 Number System)
17
 In the hexadecimal system, numbers are written
or represented with base 16.
 In the hex system, the numbers are first
represented just like in decimal system, i.e. from
0 to 9.
 Then, the numbers are represented using the
alphabets from A to F.
 The below-given table shows the representation
of numbers in the hexadecimal number system.
Dr. Ajay Nagne Dr. Ajay Nagne

18. Cont. . . . .
18
Hexa-
decima
l
0 1 2 3 4 5 6 7 8 9 A B C D E F
Decima
l
0 1 2 3 4 5 6 7 8 9 10 11 12 13 14 15
Dr. Ajay Nagne Dr. Ajay Nagne

19. 19
Decimal Binary Octal Hexadecimal
0
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
Dr. Ajay Nagne Dr. Ajay Nagne

20. 20
Name Base Symbols Example
Decimal 10
0,1,2,3,4,5,6,7,
8,9
(279)10
Binary 2 0,1 10010
Octal 8 0,1,2,3,4,5,6,7 (157)8
Hexadecimal 16
0,1,2,3,4,5,6,7,
8,9,A,B,C,D,E,F
3DB
Dr. Ajay Nagne Dr. Ajay Nagne

21. 21
Conversion from One
Number System to
Another Number system
Dr. Ajay Nagne Dr. Ajay Nagne

22. Decimal to Other Base System
22
1) Decimal to Binary No. system
2) Decimal to Octal No. system
3) Decimal to Hexadecimal No.
system
Dr. Ajay Nagne Dr. Ajay Nagne

23. 1) Decimal to Binary No. system
23
 Most Significant Bit (MSD )
The Left Most digit having the Highest
weighted Value is Call as MSD.
 Least Significant Bit (LSD)
 The right Most digit having the Lowest
weighted Value is Call as LSD.
 Ex.
2 7 8 9
MSD LSD
Dr. Ajay Nagne Dr. Ajay Nagne

24. Ex. 1 (26) 𝟏𝟎 = ( ? )2
24
2 26 0
2 13 1
2 6 0
2 3 1
2 1 1
0
Ex. 1 (26) 𝟏𝟎 = ( 11010 )2
LSB
MSB
0100/-
Dr. Ajay Nagne Dr. Ajay Nagne

25. Ex. 2 (32) 𝟏𝟎 = ( 100000)2
25
2 32 0
2 16 0
2 8 0
2 4 0
2 2 0
2 1 1
0
LSB
MSB
Dr. Ajay Nagne Dr. Ajay Nagne

26. Ex. 3 (17) 𝟏𝟎 = ( 10001 )2
26
2 17 1
2 8 0
2 4 0
2 2 0
2 1 1
0
Dr. Ajay Nagne Dr. Ajay Nagne

27. Ex. 4 (42) 𝟏𝟎 = ( ? )2
27
 Ex. 5 (125)10 = ( )2
 Ex. 6 ( 82)10 = ( )2
 Ex. 7 ( 542)10 = ( )2
 Ex. 8 ( 689)10 = ( )2
 Ex. 9 ( 1245)10 = ( )2
 Ex. 10 ( 230)10 = ( )2
Dr. Ajay Nagne Dr. Ajay Nagne

28. 2) Decimal to Octal No. system
28
Ex.
2 7 8 9
MSD LSD
Dr. Ajay Nagne Dr. Ajay Nagne

29. Ex. 1 (32) 𝟏𝟎 = (40)8
29
8 32 0
8 4 4
0
Dr. Ajay Nagne Dr. Ajay Nagne
LSD
MSD

30. Ex. 2 (50) 𝟏𝟎 = ( 62 )8
30
8 50 2
8 6 6
0
Dr. Ajay Nagne Dr. Ajay Nagne
LSD
MSD
Ex. 2 (50) 𝟏𝟎 = ( 26 )8

31. Ex. 3 (17) 𝟏𝟎 = ( 21 )8
31
8 17 1
8 2 2
0
Dr. Ajay Nagne Dr. Ajay Nagne

32. Ex. 3 (128) 𝟏𝟎 = (200)8
32
8 128 0
8 16 0
8 2 2
0
Dr. Ajay Nagne Dr. Ajay Nagne
LSD
MSD

33. Ex. 4 (42) 𝟏𝟎 = ( ? )8
33
 Ex. 5 (76)10 = (114 )8
 Ex. 6 ( 82)10 = (122 )8
 Ex. 7 ( 98)10 = ( 142 )8
 Ex. 8 ( 128)10 = ( 1200 )8 ( 200 )8
 Ex. 9 ( 245)10 = ( 365 )8
 Ex. 10 ( 1245)10 =( 2335 )8
Dr. Ajay Nagne Dr. Ajay Nagne

34. 3) Decimal to Hexadecimal No.
system
34
Ex.
2 7 8 9
MSD LSD
Dr. Ajay Nagne Dr. Ajay Nagne

35. Ex. 1 (22) 𝟏𝟎 = ( 16)16
35
16 22 6
16 1 1
0
Dr. Ajay Nagne Dr. Ajay Nagne
LSD
MSD

36. Ex. 2 (40) 𝟏𝟎 = ( 29)16
36
16 41 9
16 2 2
0
Dr. Ajay Nagne Dr. Ajay Nagne
LSD
MSD

37. Ex. 3 (45) 𝟏𝟎 = ( 2D )16
37
16 45 13 D
16 2 2 2
0
Dr. Ajay Nagne Dr. Ajay Nagne
LSD
MSD

38. Ex. 4 (95) 𝟏𝟎 = ( 5F )16
38
16 95 15 F
16 5 5
0
Dr. Ajay Nagne Dr. Ajay Nagne
LSD
MSD

39. Ex. 5 (142) 𝟏𝟎 = ( 8E)16
39
 Ex. 6 (125)10 = ( 7D )16
 Ex. 7 ( 82)10 = ( 52 )16
 Ex. 8 ( 542)10 = ( 21E )16
 Ex. 9 ( 689)10 = ( )16
 Ex. 10 ( 1245)10 = ( )16
 Ex. 11 ( 230)10 = ( )16
Dr. Ajay Nagne Dr. Ajay Nagne

40. Ex. 4 (95) 𝟏𝟎 = ( 5F )16
40
16 542 14 E
16 33 1 1
16 2 2 2
0
Dr. Ajay Nagne Dr. Ajay Nagne
LSD
MSD

41. 41
Thank You . . . . . !
Dr. Ajay Nagne Dr. Ajay Nagne