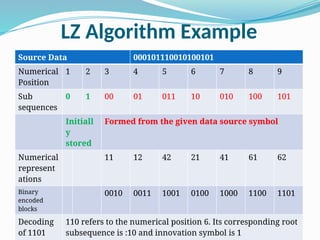
The document discusses Lempel-Ziv coding and contrasts it with Huffman coding, highlighting that LZ coding achieves higher compaction rates (55% compared to 43% for Huffman). It details the steps of the LZ algorithm, which involves parsing data, forming a codebook, and creating binary representations of subsequences. Additionally, it explains the concept of the innovation symbol in LZ coding, which distinguishes subsequences in the codebook.

1. DIGITAL COMMUNICATION –
INFORMATION THEORY
Lempel Ziv Coding
Dr.G.Suchitra,
Assistant Professor,
Department of ECE,
Government College of Technology,
Coimbatore

2. Lempel Ziv Coding

3. Huffman coding Drawbacks
 Huffman coding requires knowledge of the
probabilistic model of the source
 Source statistics should be known apriori
 Does not capture the higher order relationships
between words and phrases in modeling txt
since it requires large storage capacity

4.  LZ algorithm uses fixed length codes to represent
variable number of source symbols
 Hence this algorithm is more suitable for
synchronous transmission
 When applied to English Text, Compaction
achieved in
Huffman coding : 43%
LZ algorithm : 55%

5. Lempel Ziv Coding Algorithm
1. Parse the source data stream into segments
2. These segments are the shortest subsequences
that are not encountered previously. Continue
this until the entire data stream is finished
3. Form a code book using these data
subsequences
4. Form the numerical representations of the
individual sequences in the codebook
5. Form the binary encoded representation of the
different subsequences of the data stream

6.  The last symbol of each subsequence in the
codebook is called innovation symbol. Its
appendage to a particular subsequence
distinguishes itself from all the previous
subsequences stored in the code book
 If the fixed binary code length is 12 bits, then
number of possible codebook entries is 4096.

7. LZ Algorithm Example
Source Data 000101110010100101
Numerical
Position
1 2 3 4 5 6 7 8 9
Sub
sequences
0 1 00 01 011 10 010 100 101
Initiall
y
stored
Formed from the given data source symbol
Numerical
represent
ations
11 12 42 21 41 61 62
Binary
encoded
blocks
0010 0011 1001 0100 1000 1100 1101
Decoding
of 1101
110 refers to the numerical position 6. Its corresponding root
subsequence is :10 and innovation symbol is 1

8. REFERENCES
1.“Digital Communication”, Simon Haykin, Wiley India,
2.“Statistical theory of Communication”, S.P.Eugene
Xavier, New Age International Publishers.
3.“Modern Analog and Digital Communication”, B.P.Lathi,
Oxford University Press,

9. THANK YOU