1. 数学的思考とは
~数学を通して、『頭の働かせ方』を身につける~

2. 本日の授業は……
本日の授業は、「所得倍増計画」を例に、
・数学的とは、どういうことか？
・数学的問題とは？
・数学的思考とは？
について、一緒に実践していきます。

3. 「所得倍増計画」（1960年,池田内閣）
1961年から１０年間で、
国民所得（国民総生産）を２倍にする。
そのために、年率７％の成長を目標とする。
1960年のGDPは約13兆円なので、1970年に
約26兆円にする

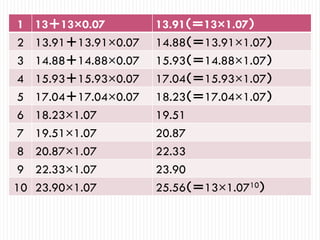
4. 1 13＋13×0.07 13.91（＝13×1.07）
2 13.91＋13.91×0.07 14.88（＝13.91×1.07）
3 14.88＋14.88×0.07 15.93（＝14.88×1.07）
4 15.93＋15.93×0.07 17.04（＝15.93×1.07）
5 17.04＋17.04×0.07 18.23（＝17.04×1.07）
6 18.23×1.07 19.51
7 19.51×1.07 20.87
8 20.87×1.07 22.33
9 22.33×1.07 23.90
10 23.90×1.07 25.56（＝13×1.0710）

5. 問１．年率10％では、10年後どうなるでしょうか？
解答
年率７％の場合…13×（1+0.07）10=25.48
（兆円）
より、
年率１０％の場合…13×（1+0.10）10=33.67
（兆円）
（1.0710=1.96 と 1.110=2.59 は、用いて良い）

6. 問２．年率７％では、20年後どうなるでしょうか？
解答
10年後…13×（1+0.07）10=25.48（兆円）
より、
20年後…13×（1+0.07）20=50.18（兆円）
（1.0720＝3.86 は、用いて良い）

7. ＜所得倍増計画＞
1961年から１０年間で、GDPを２倍にする。そのために、
年率７％の成長を目標とする。
10年間で ７％成長すると GDPが ２倍になる
13×（1+0.07）10=25.48
10年間で 10％成長すると GDPが ２.６倍になる
13×（1+0.10）10=33.67
20年間で ７％成長すると GDPが ４倍になる
13×（1+0.07）20=50.18

8. 数学的思考とは？
数学的な問題に対する「頭の働かせ方」
・年率10％では、10年後どうなるか？
・年率 7％では、20年後どうなるか？

9. 「所得倍増計画」に関する数学的な問題を作ろう！
問．10年後に３倍にするには、何％成長すれば良いか？
10年間で A％成長すると GDPが ３倍になる
13×（1+A×0.01）10=13×3
解答 （1+A×0.01）10=3 となればよいから
1.110=2.59, 1.1110=2.83,1.1210=3.11
より、
∴ 11～12％成長すれば、3倍となる

10. 「所得倍増計画」に関する数学的な問題を作ろう！
問．年率10％で２倍にするには、何年かかるか？
N年間で 10％成長すると GDPが ２倍になる
13×（1+0.10）N＝13×2
解答 （1+0.10）N=3 となればよいから
1.110=2.59, 1.18=2.14, 1.17=1.94
より、
∴ 7～8年後に、2倍となる。

11. 「所得倍増計画」を一般化してみましょう！
○年間で △％成長すると GDPが □倍になる
（1+△×0.01）◯＝□
1961年から○年で、
国民所得（国民総生産）を□倍にする。
そのために、年率△％の成長を目標とする。
N年間で A％成長すると GDPが T倍になる
（1+A×0.01）N＝T

12. 数学的思考とは？
数学的な問題に対する「頭の働かせ方」
・ 「問題が何か？」を吟味する
・ 「問題となっていること」を整理・整頓する
・ 解くための方法を探索し、計画する
・ 解答までの計画を実行する
・ 問題を一般化する

13. 本日のまとめ
１．所得倍増計画を数学的な問題として捉える
２．問題に対する解答を計画し、実行する
３．問題を一般化する
「所得倍増計画」を数学的に思考すると…