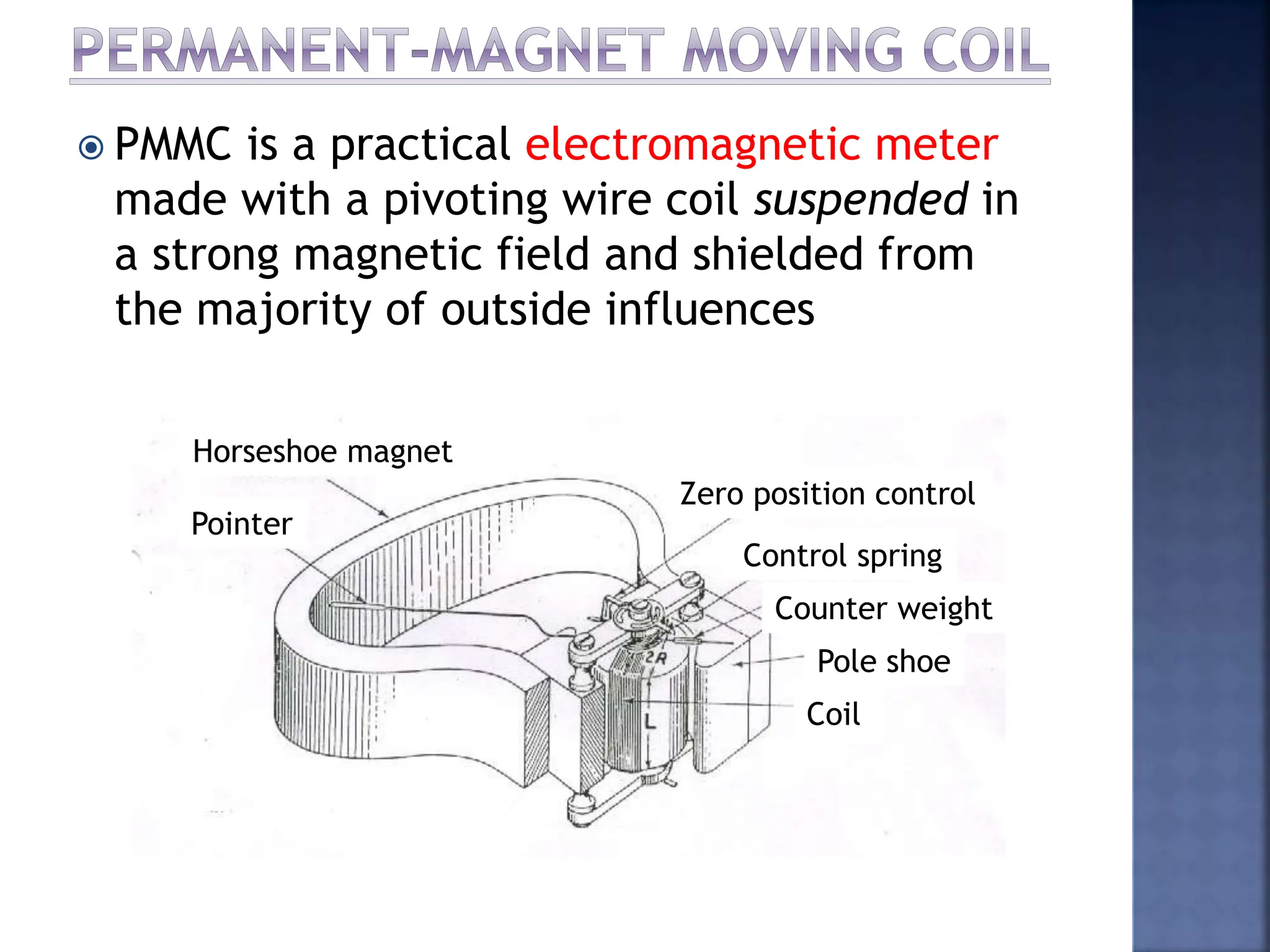
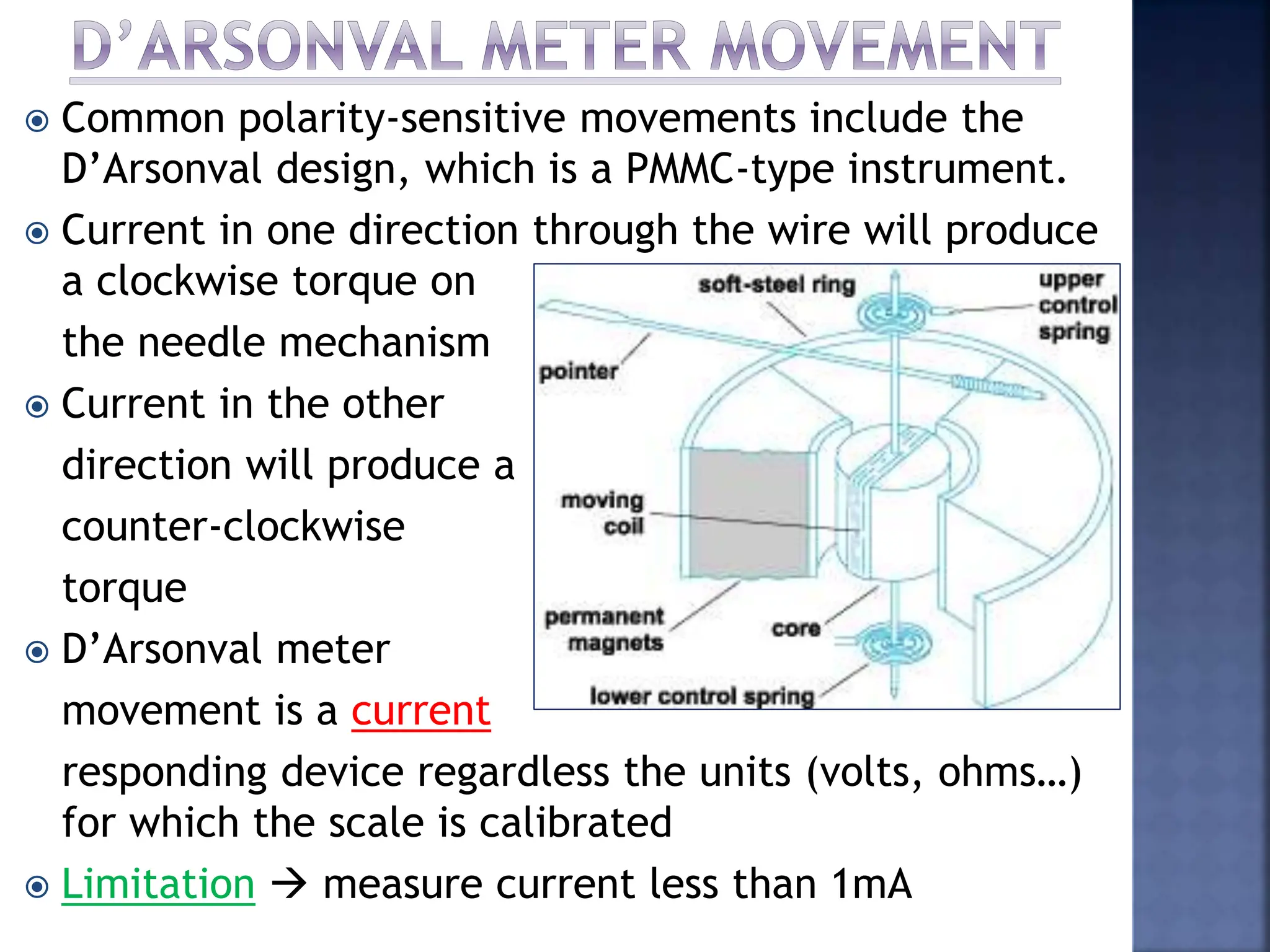
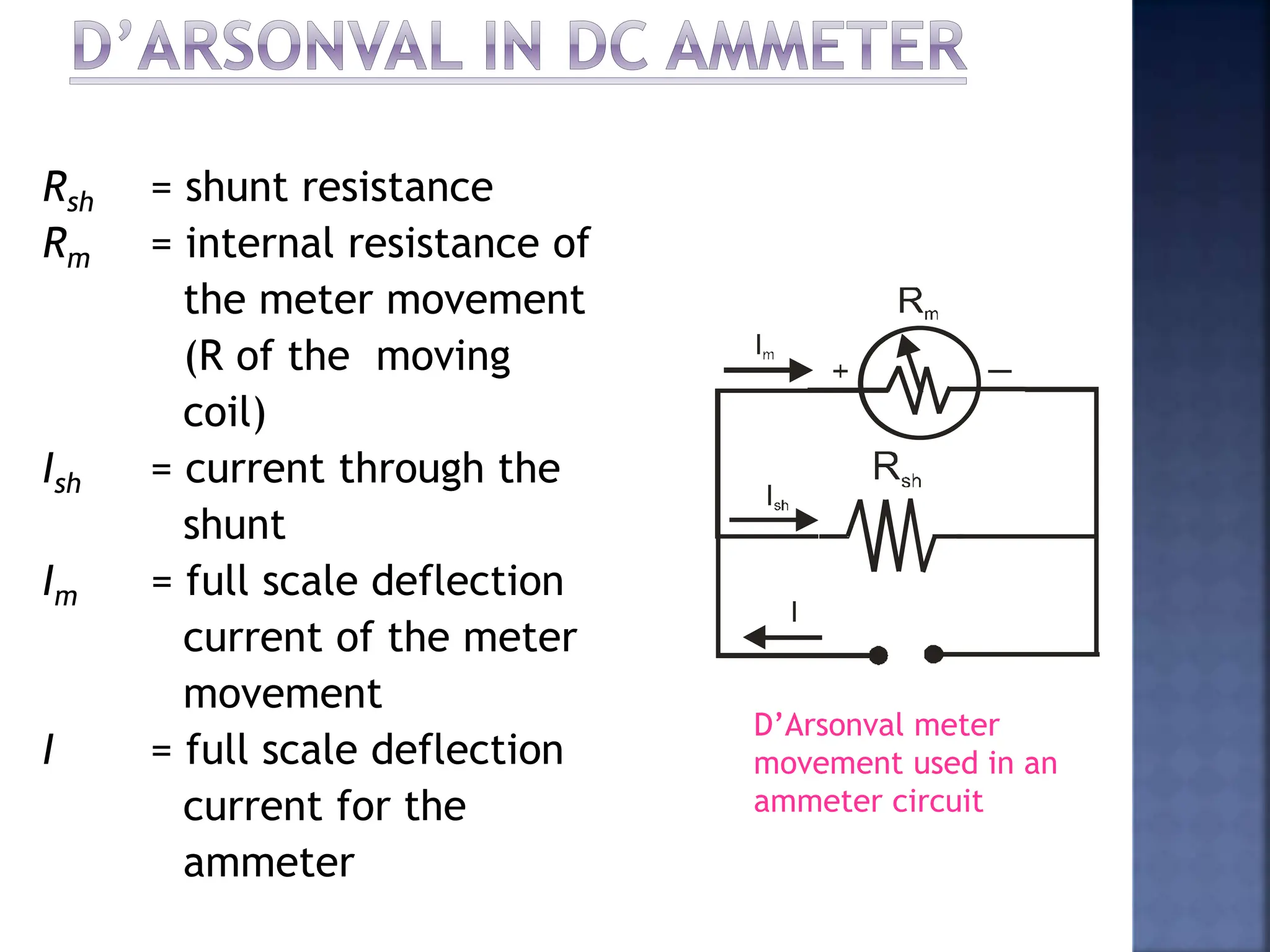
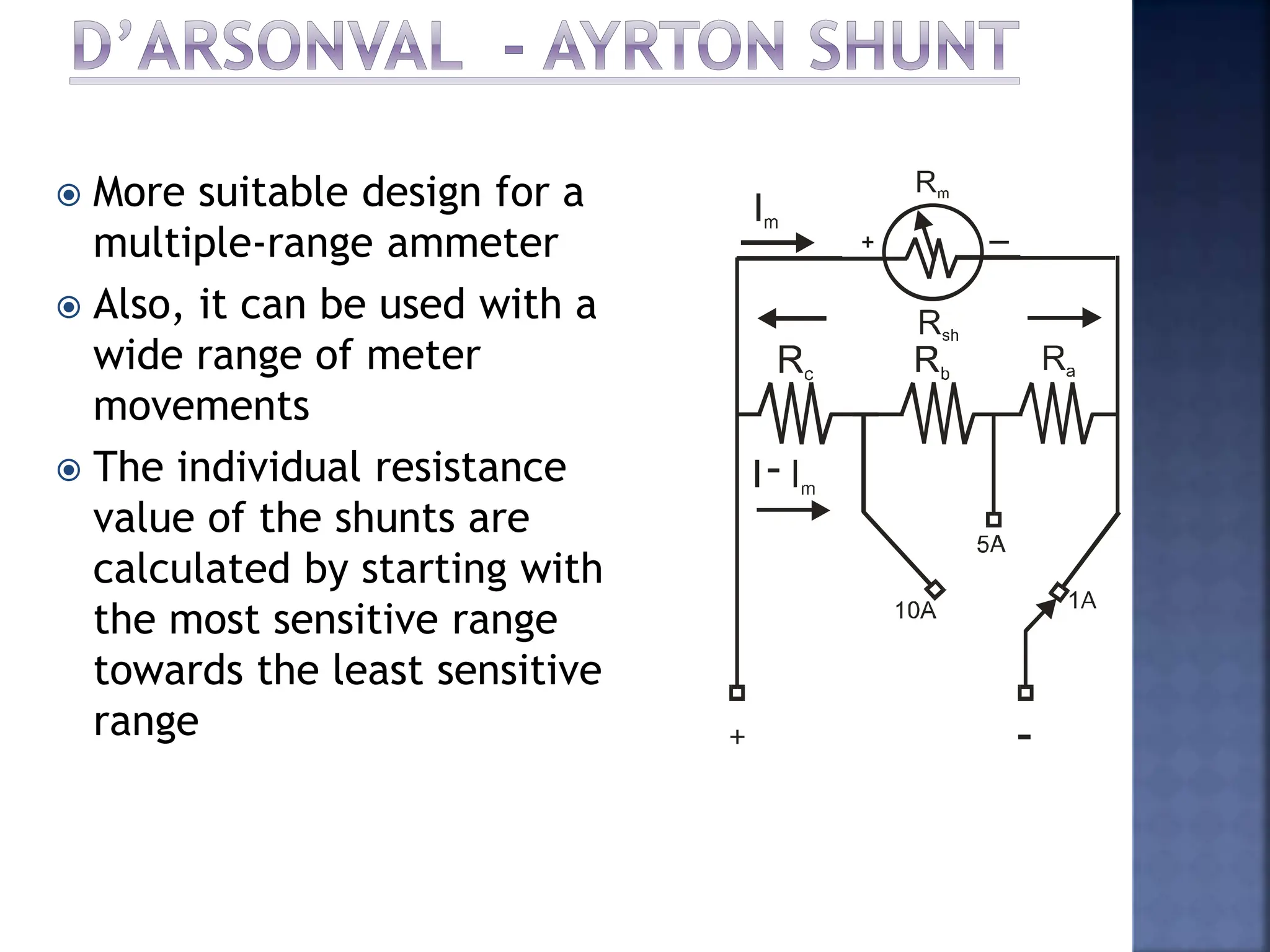
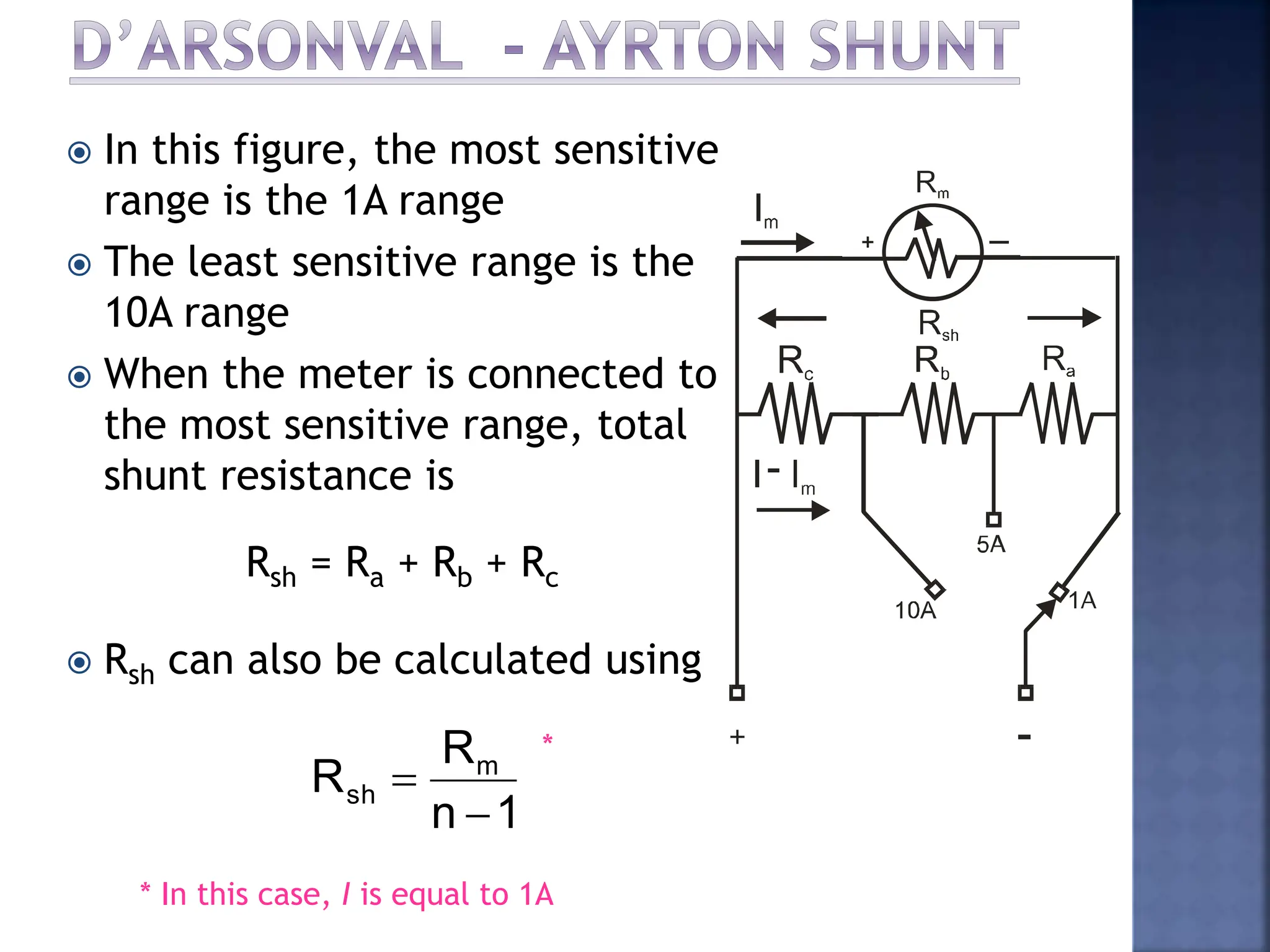
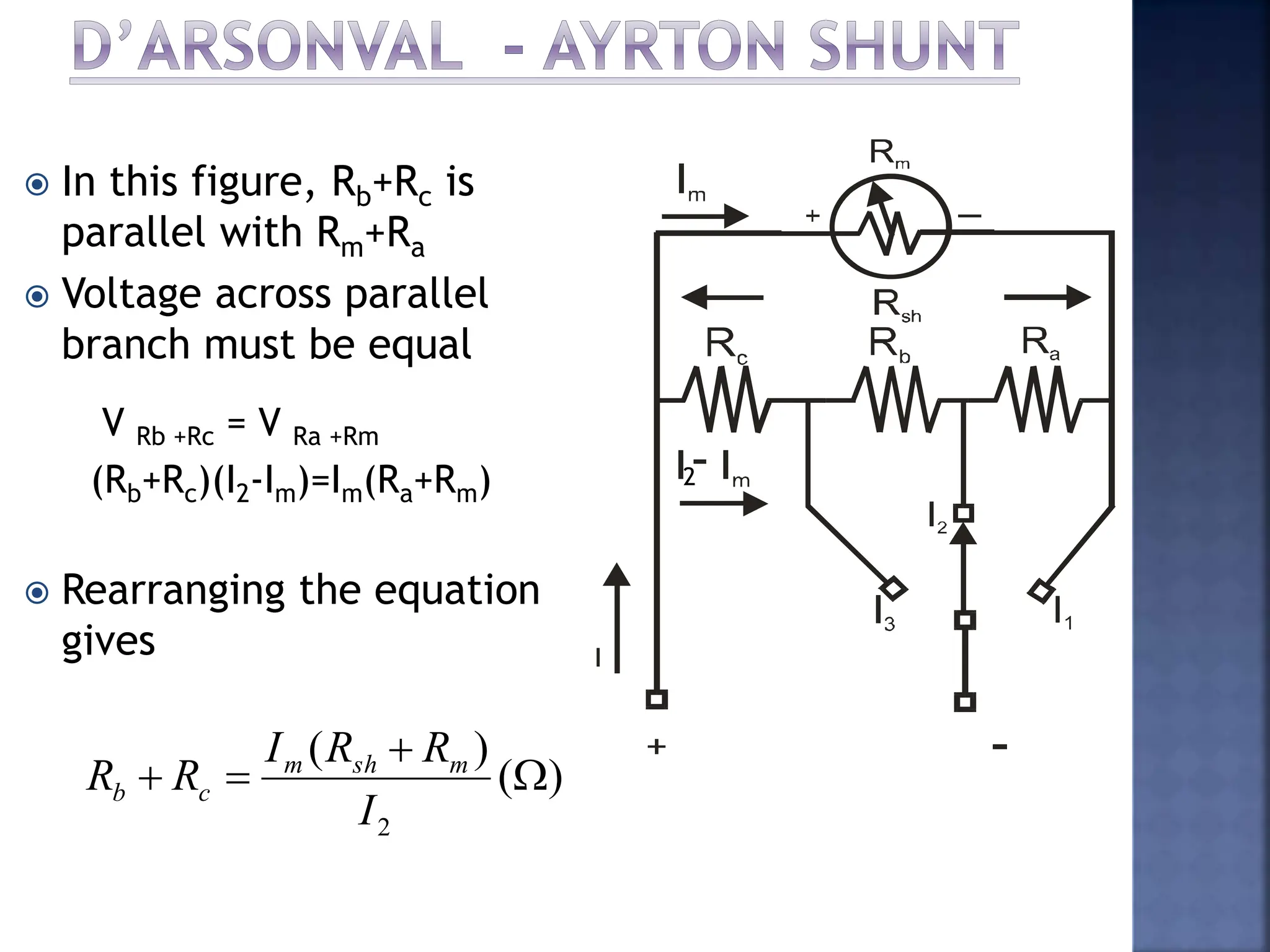
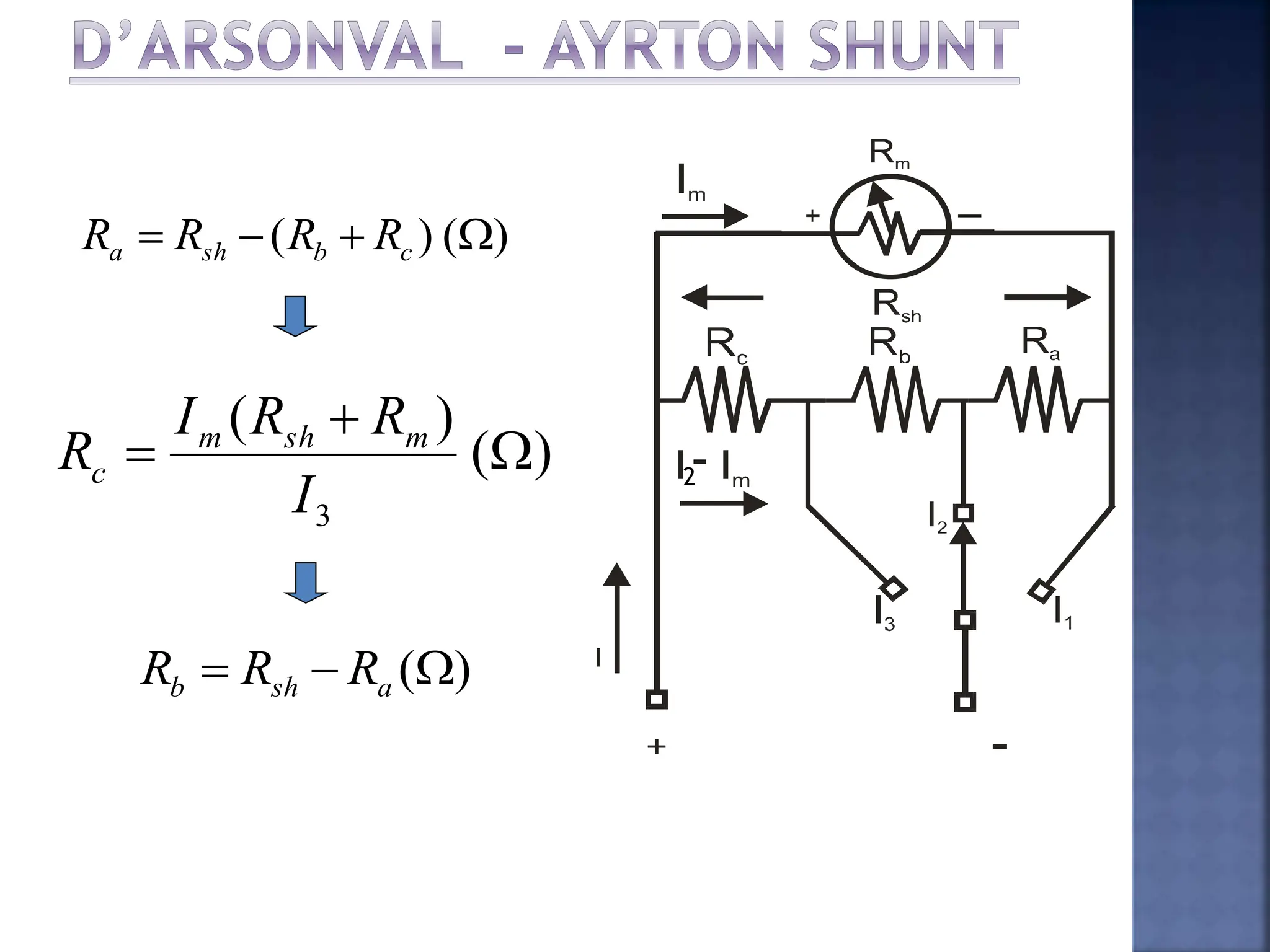
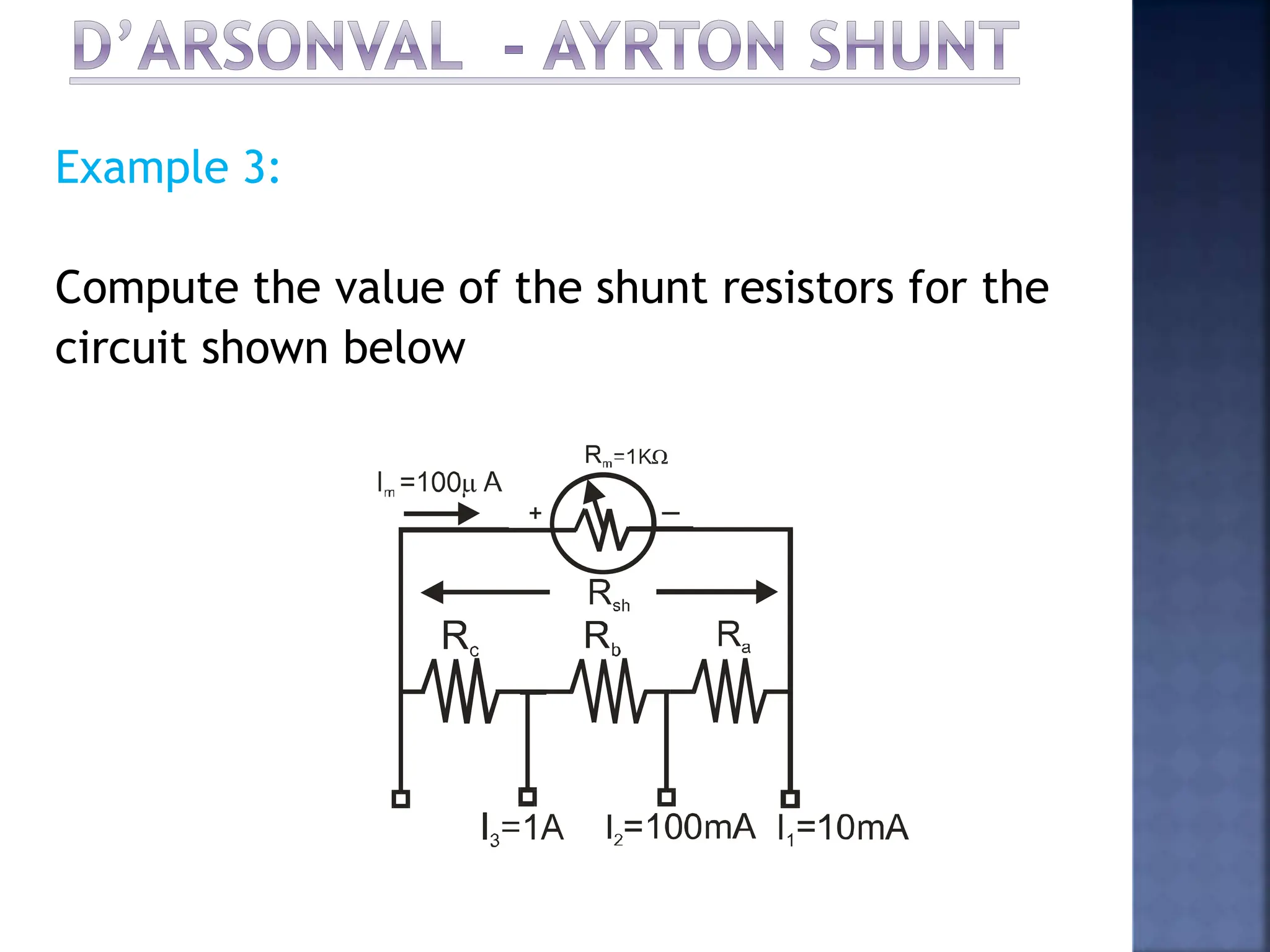
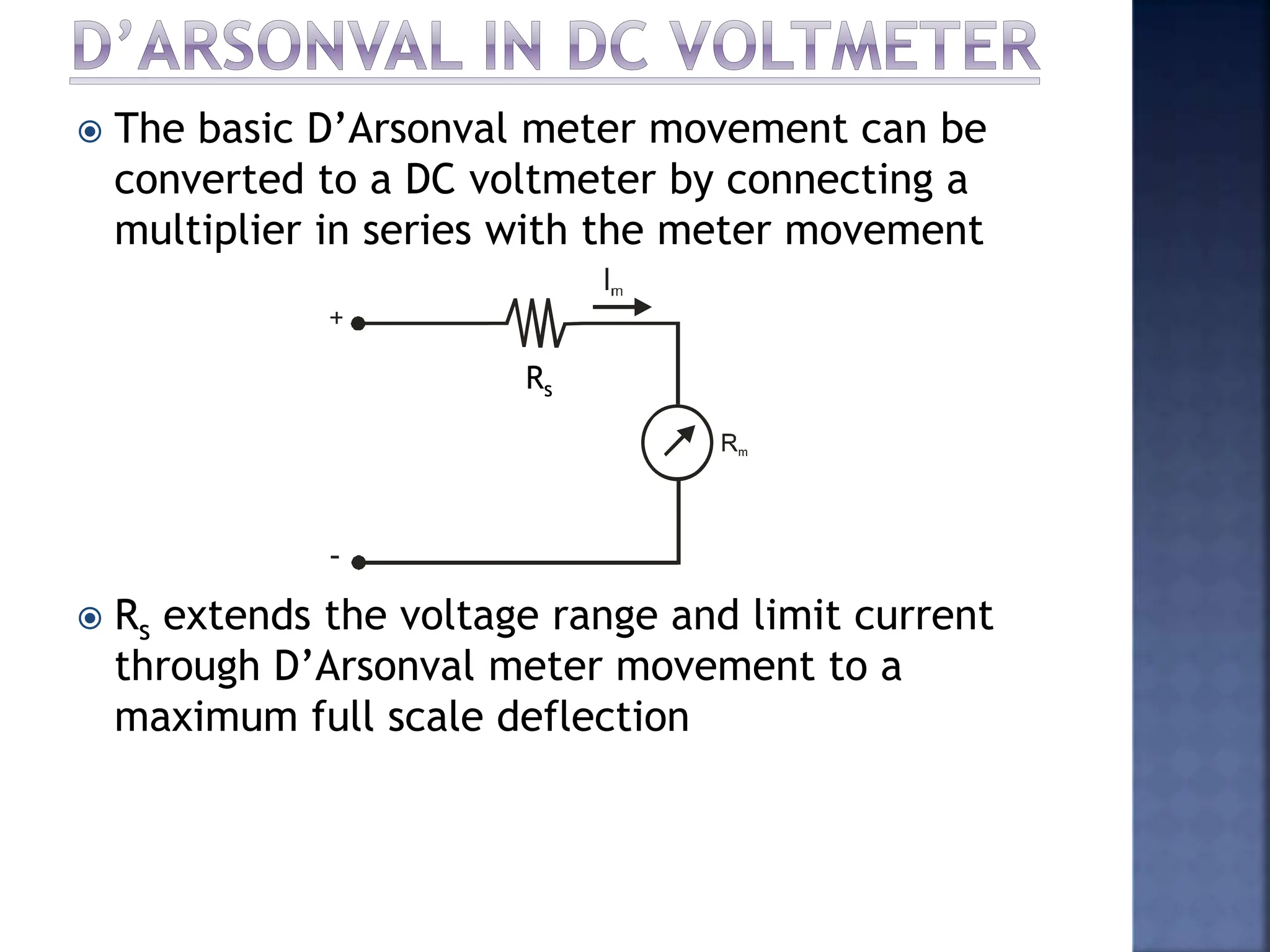
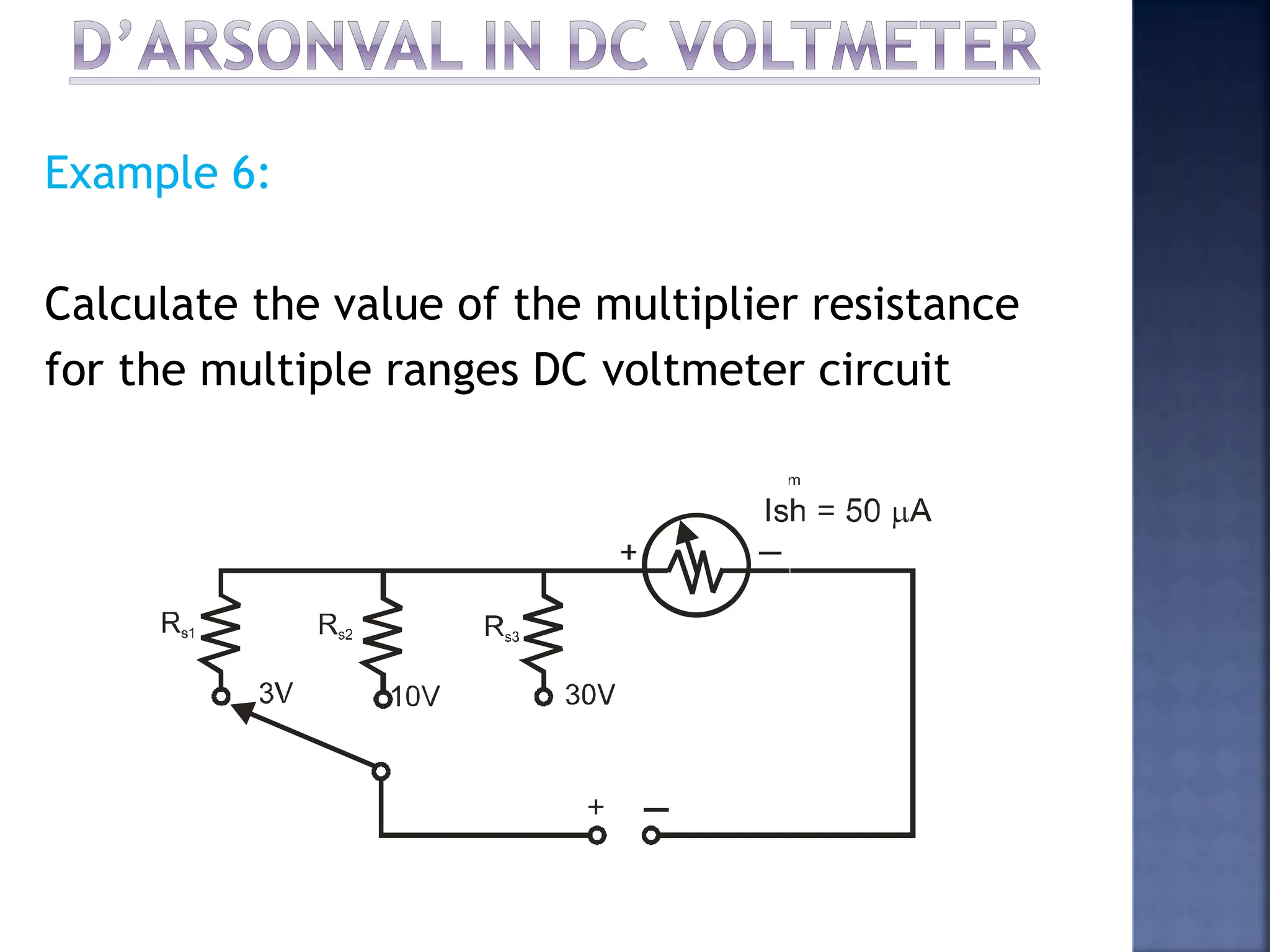
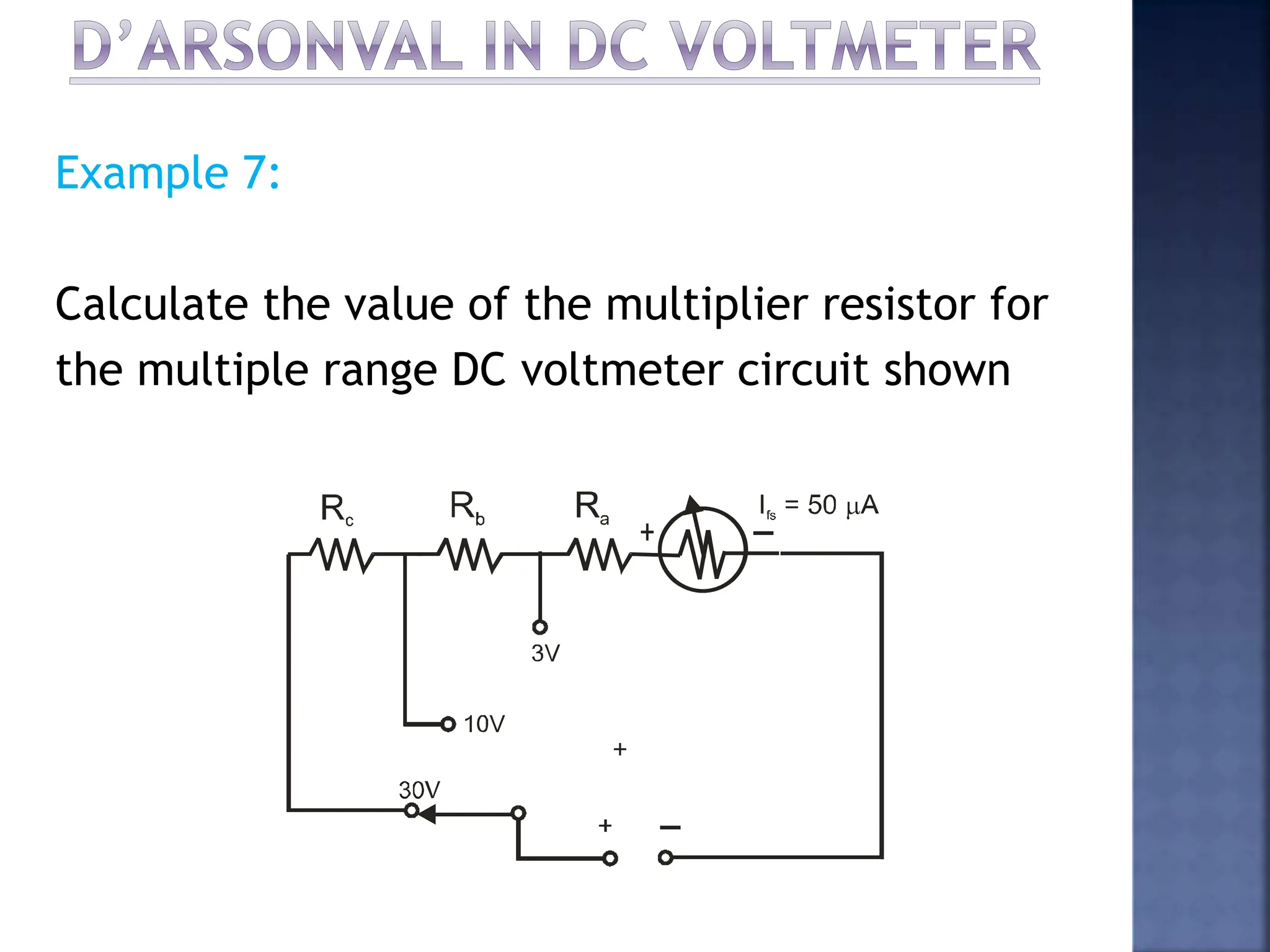
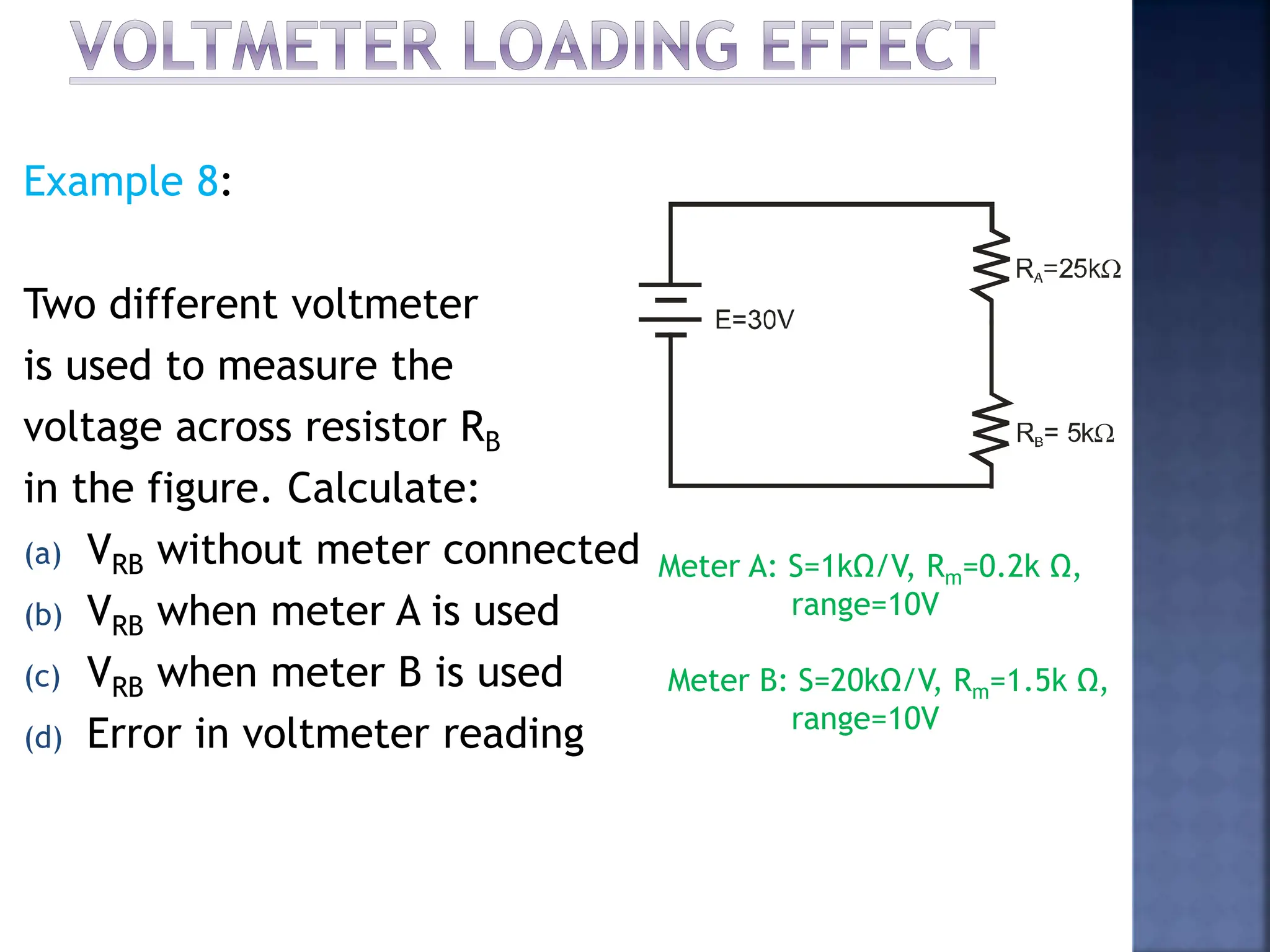
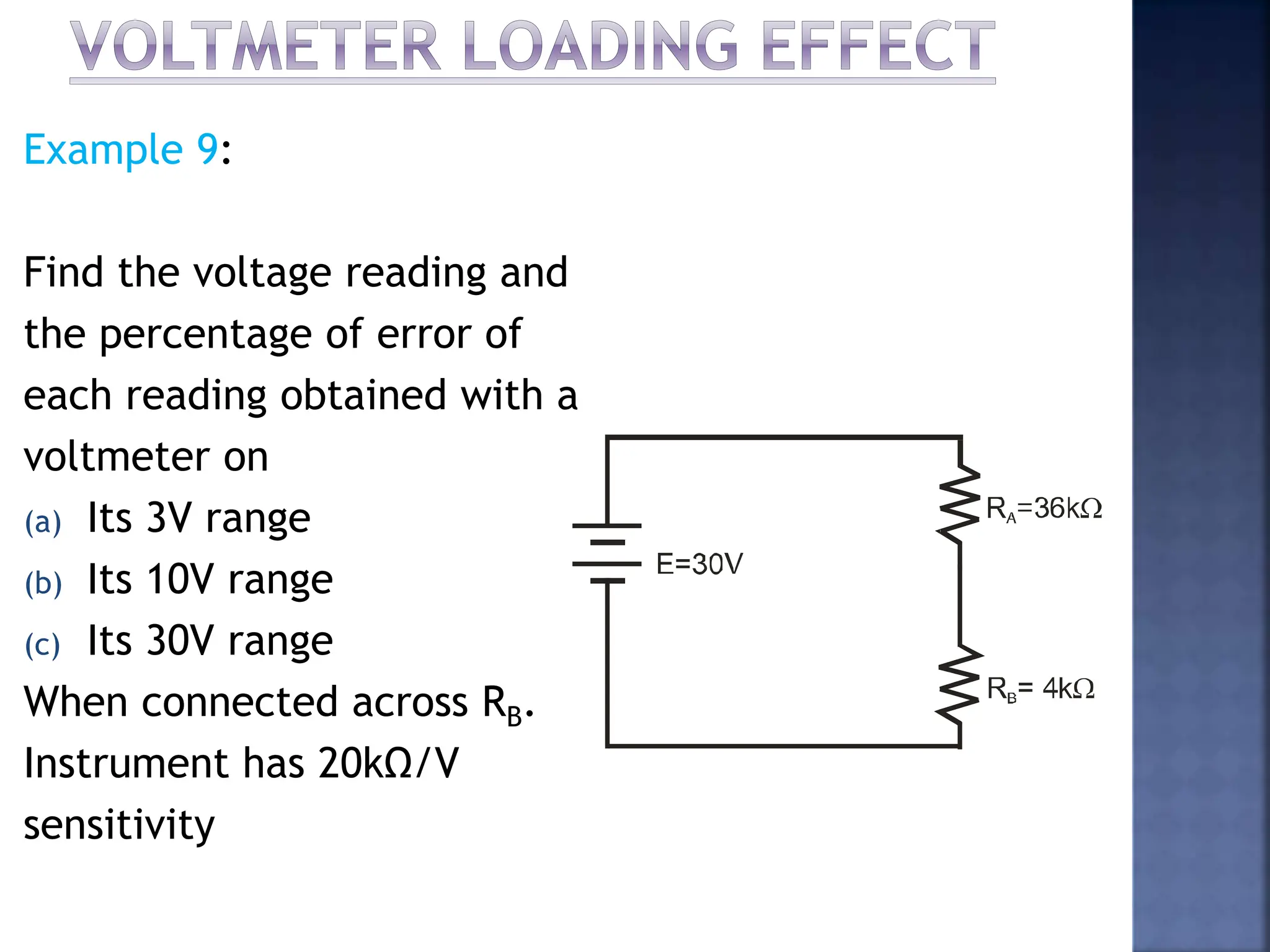
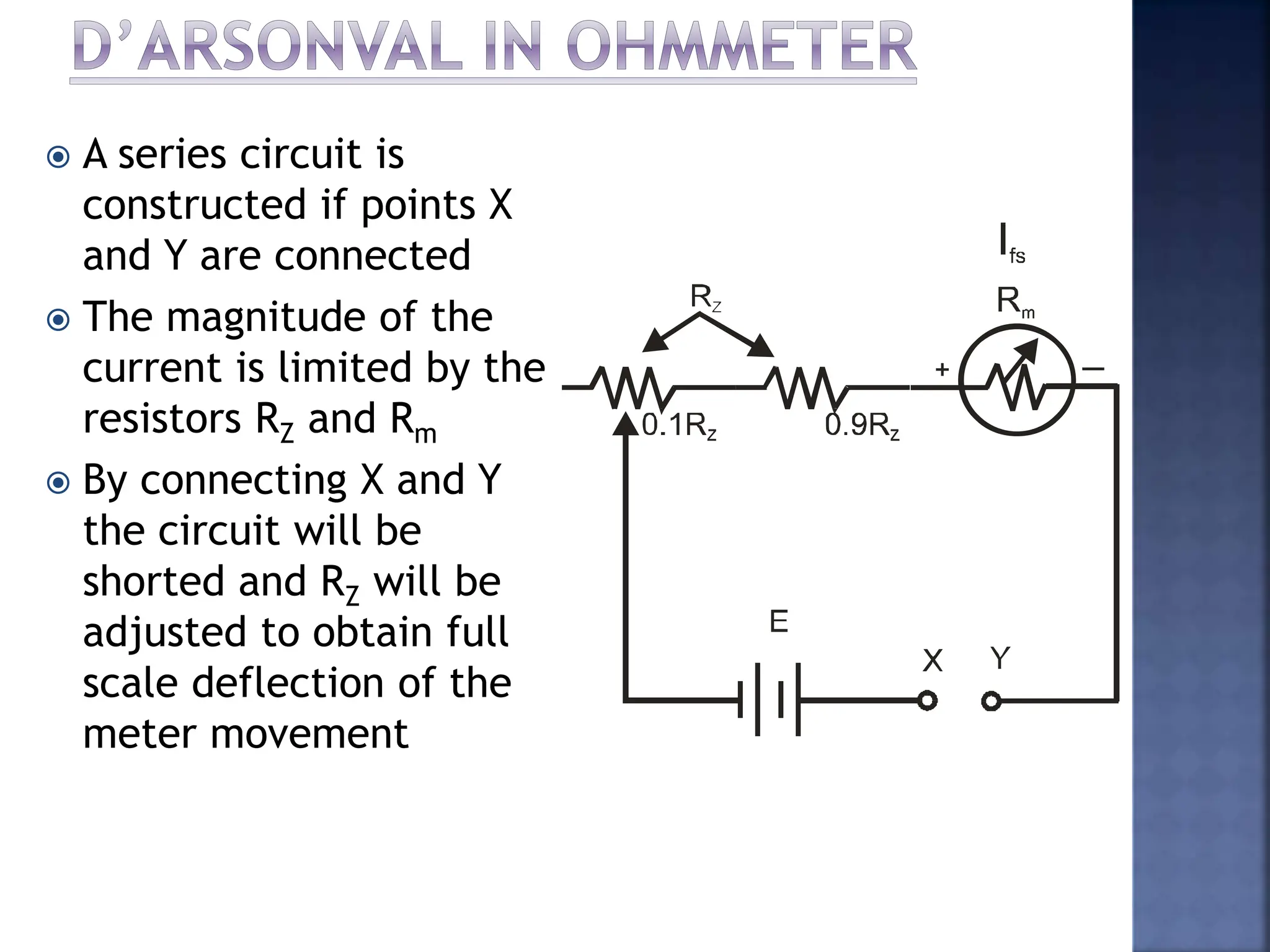
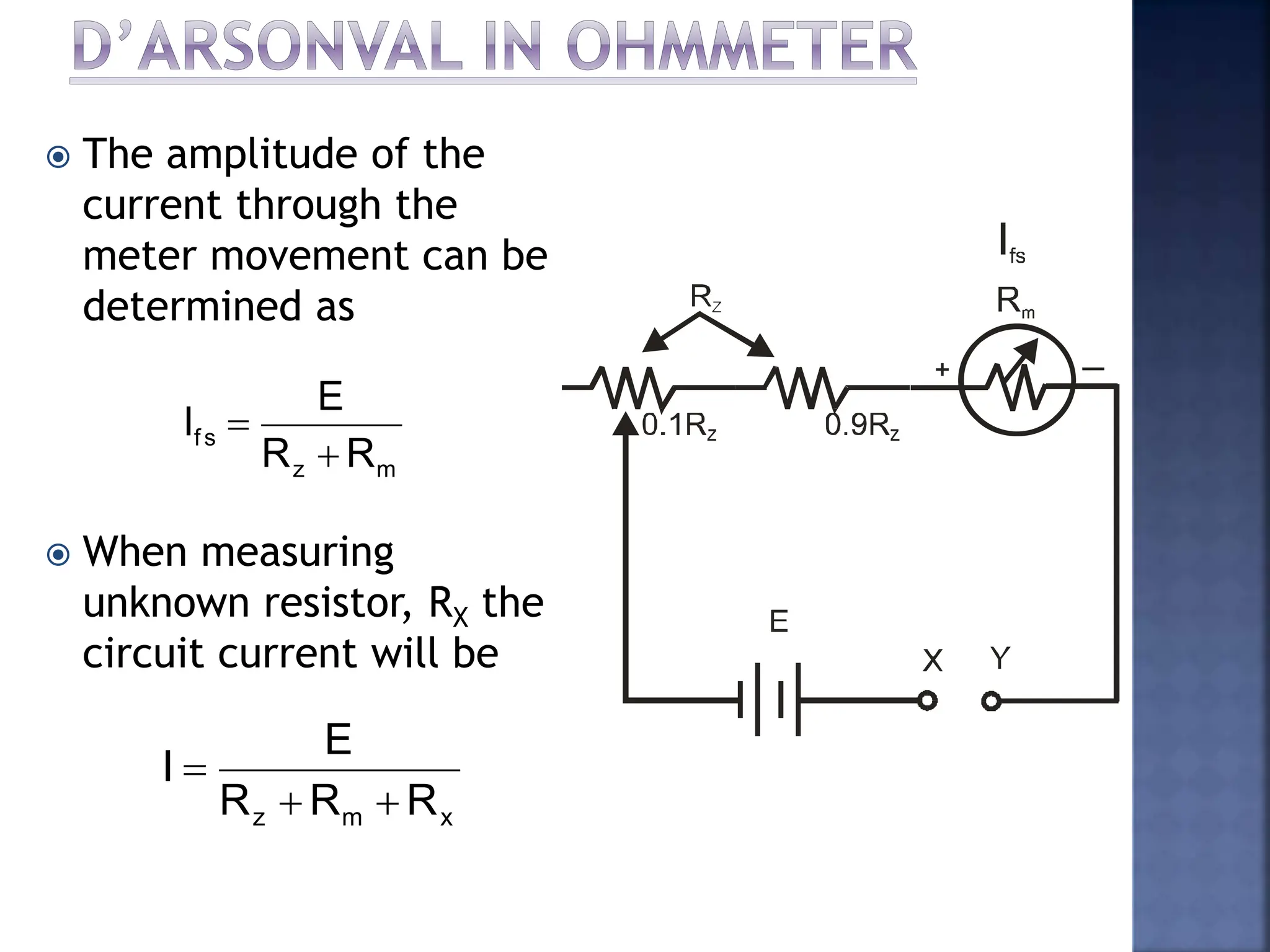
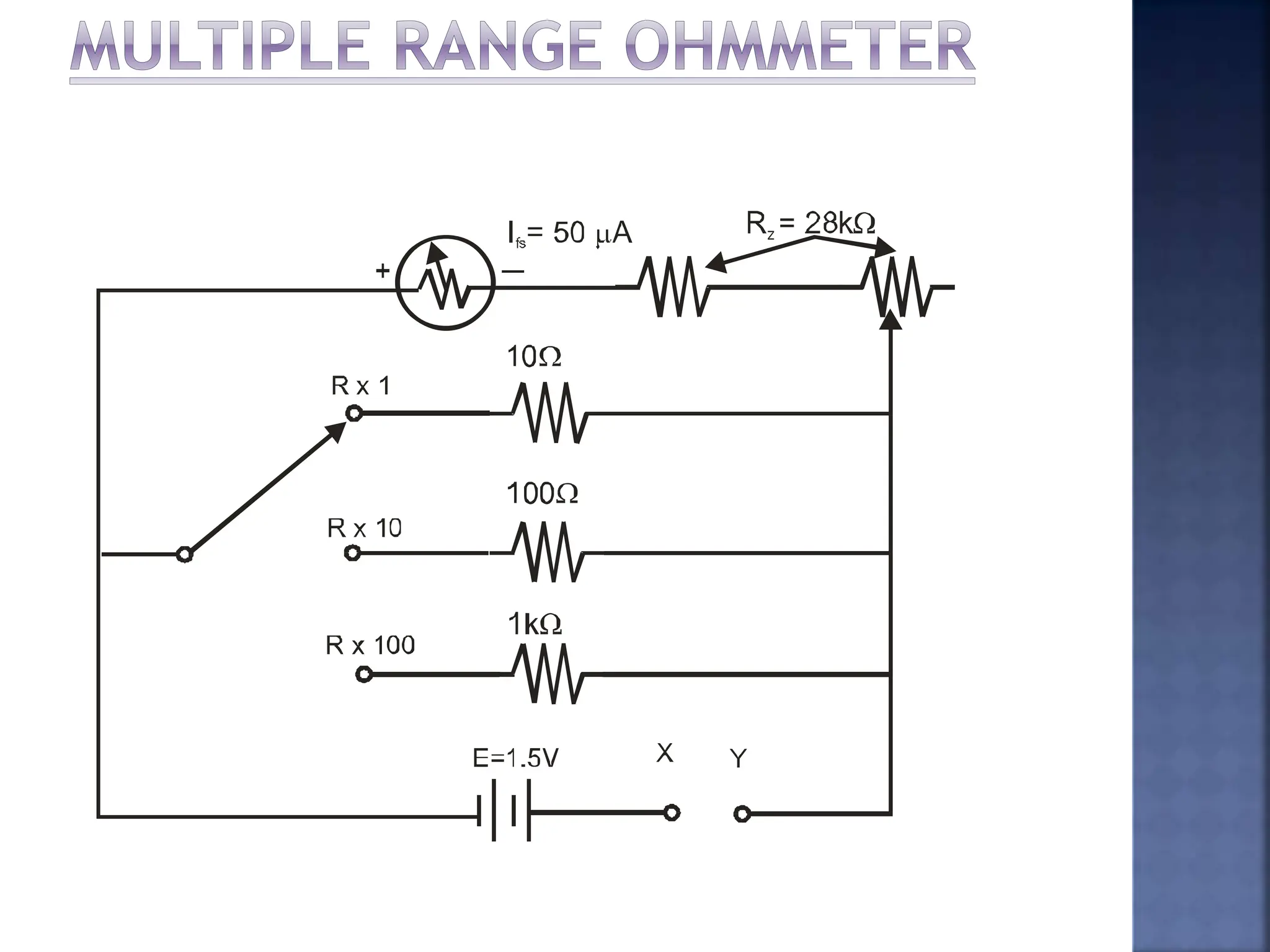
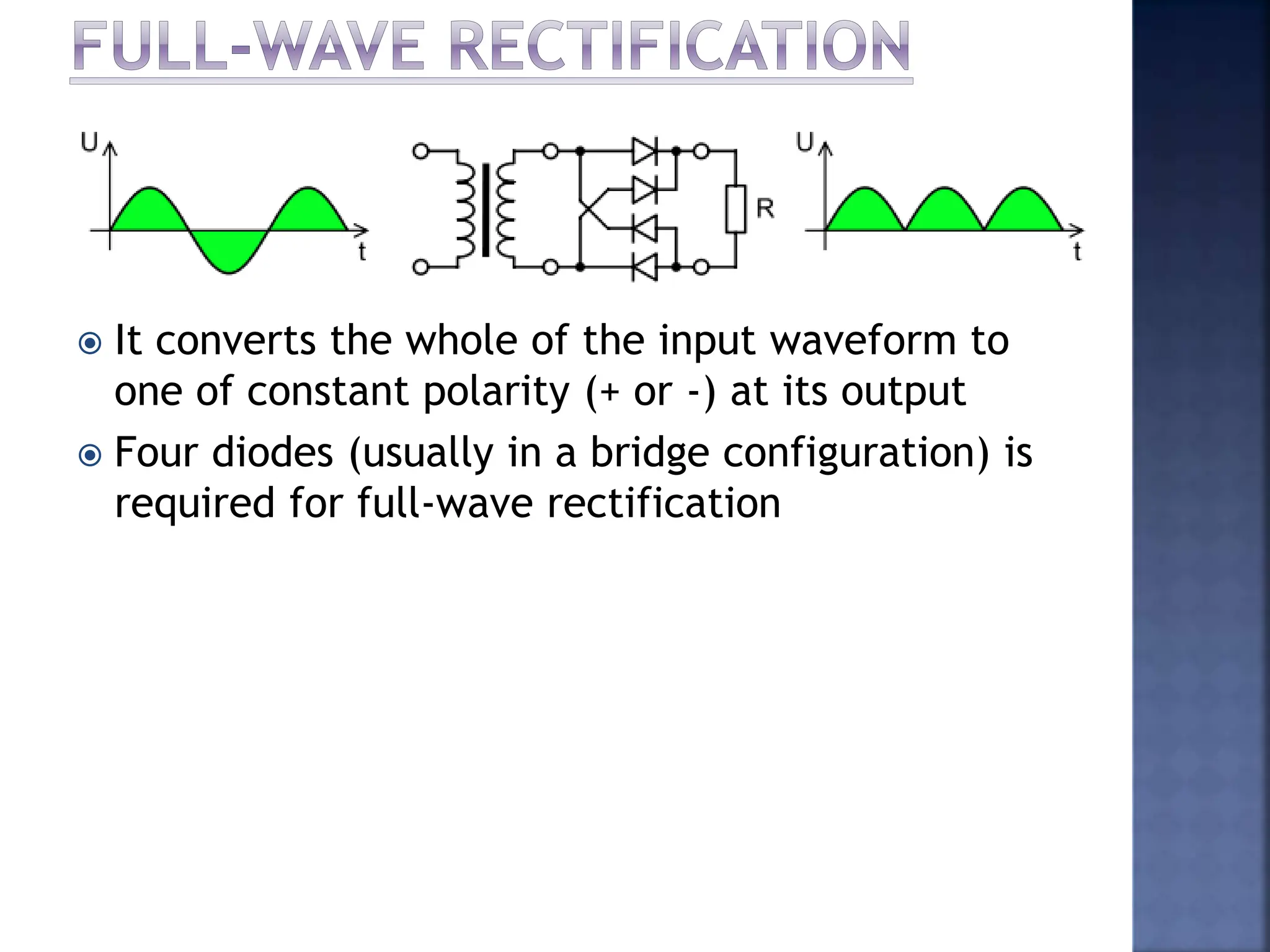
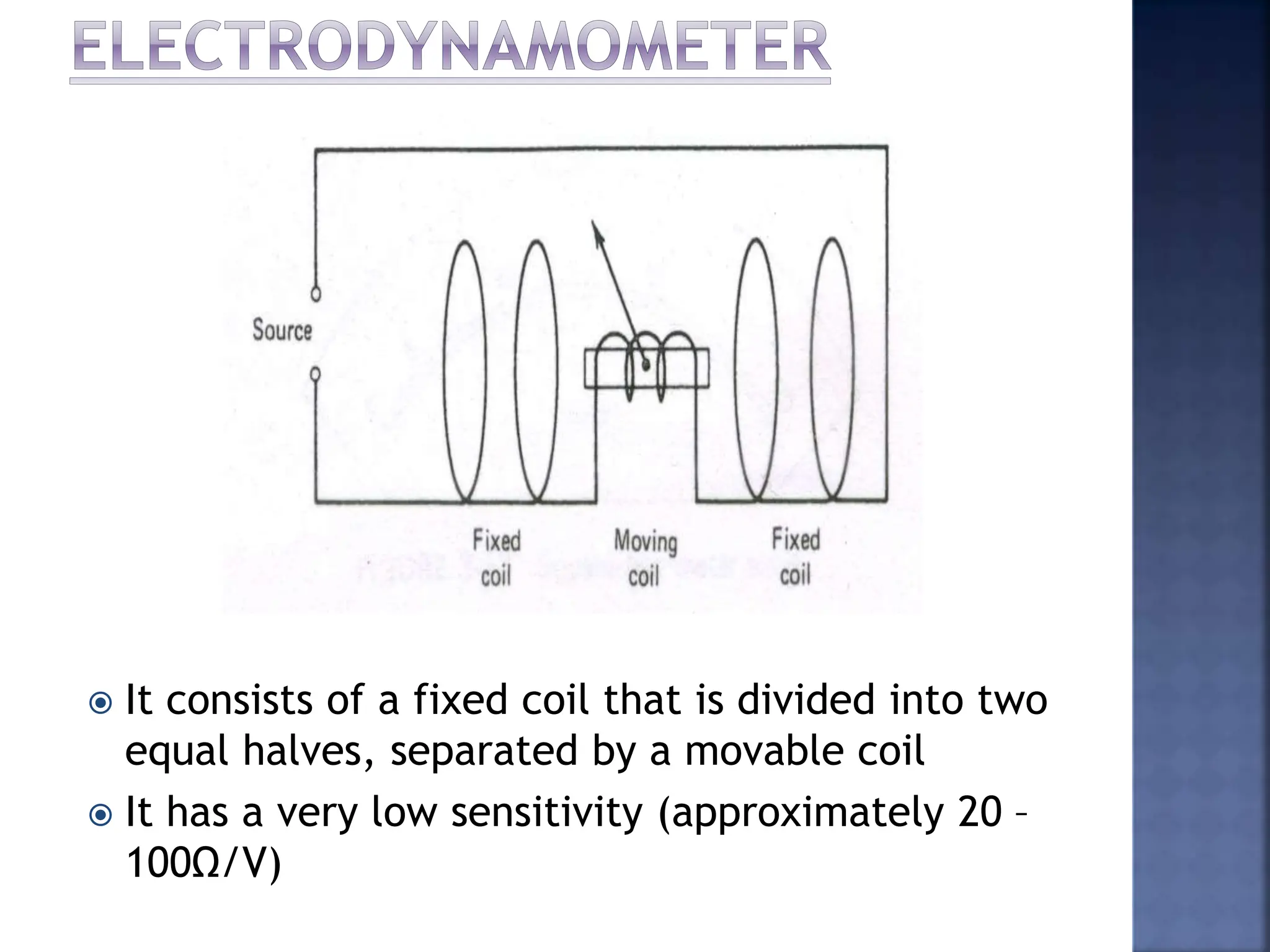
This document discusses different types of meters used to measure direct current (DC) and alternating current (AC). It describes common meter movements like the D'Arsonval meter and how they can be modified with shunt resistors or multipliers to measure different electrical quantities like voltage, current, and resistance. It also discusses issues like loading error that can occur when measuring voltage with a voltmeter. Finally, it covers techniques like half-wave and full-wave rectification that allow D'Arsonval meters to be used for measuring AC signals.

1. DC and AC meters
Hasmawati Antong
Lecturer
Department of Mechatronics Engineering
International Islamic University Malaysia
hasmawati@iium.edu.my

2. DC
METERS

3.  Introduction to meter
 Galvanometer
 Permanent-magnet moving coil
 D’Arsonval meter movement
 D’Arsonval in DC ammeter
 D’Arsonval – Ayrton Shunt
 D’Arsonval in DC voltmeter
 Voltmeter loading effect
 D’Arsonval in ohmmeter
 Multiple range ohmmeter

4.  A meter is any device built to accurately
detect and display an electrical quantity in a
form readable by a human being
 Usually this “readable form” is visual:
- motion of a pointer on a scale
- a series of lights arranged to form a
“bargraph”
- a display composed of numerical figures
 In the analysis and testing of circuits, there
are meters designed to accurately measure
voltage, current and resistance.

5. AC voltage
Current
Resistance
DC voltage

6.  Most modern meters are DIGITAL  their
readable display is in the form of numerical
digits
 Older designs of meters uses a pointer device
to display the quantity being measured
 In either case, the principle adopted for the
display mechanism are the same
 The display mechanism of meter is called
meter movement
 The first meter movement were known as
GALVANOMETERS

7.  A simple galvanometer is
made from a magnetized
needle suspended from a
string and positioned within
a coil of wire
 Current through the wire coil
produces magnetic field
which deflects the needle
from pointing in the direction
of earth’s magnetic field
 Nowadays, the term galvanometer usually refers to
any design of electromagnetic meter movement
built such as permanent-magnet moving coil (PMMC)

8.  PMMC is a practical electromagnetic meter
made with a pivoting wire coil suspended in
a strong magnetic field and shielded from
the majority of outside influences
Horseshoe magnet
Pointer
Zero position control
Control spring
Counter weight
Pole shoe
Coil

9. Working Principle
 Current to be measured is directed through the
coils of the electromagnet
 Magnetic field produced by the current opposed
the field of the permanent magnet and causes
rotation of the magnet core
 The core is restrained by springs so that the
needle will move in proportion to the current
intensity
 The more current applied to the core, the
stronger the opposing field, and the larger the
needle deflection
 When the current is stopped, the opposing field
collapsed and the needle return to zero

10.  The arc on the meter
display is labeled
with numbers to
indicate the value of
the quantity being
measured
 An increased in
measured current drives the
needle to the right
 A decrease in measured current causes the needle to
drop back to its resting position on the left
 Most meter movements are polarity-sensitive  one
direction of current drive the needle to the right and
the other driving it to the left

11.  Common polarity-sensitive movements include the
D’Arsonval design, which is a PMMC-type instrument.
 Current in one direction through the wire will produce
a clockwise torque on
the needle mechanism
 Current in the other
direction will produce a
counter-clockwise
torque
 D’Arsonval meter
movement is a current
responding device regardless the units (volts, ohms…)
for which the scale is calibrated
 Limitation  measure current less than 1mA

12.  A modification is needed to increase the range of
current that can be measured by the basic meter
movement
 A low resistance, shunt resistance (Rsh) is placed
parallel to the meter movement resistance, Rm
 Rsh will provide an alternate path for the total
metered current around the meter movement
 In most circuit,
Ish > Im

13. Rsh = shunt resistance
Rm = internal resistance of
the meter movement
(R of the moving
coil)
Ish = current through the
shunt
Im = full scale deflection
current of the meter
movement
I = full scale deflection
current for the
ammeter
D’Arsonval meter
movement used in an
ammeter circuit

14.  Voltage drop across the meter movement is
 The voltage drop across the shunt and meter
movement is the same.
 The current through the shunt is
 Therefor Rsh is
m
m
m R
I
V 
m
sh V
V 
m
sh I
I
I 

)
(
R
I
I
I
R
I
I
I
R
I
I
V
R m
m
m
m
sh
m
sh
m
m
sh
sh
sh 







15. Example 1:
Calculate the value of the shunt resistance required
to convert a 1mA meter movement, with a 100Ω
internal resistance into a 0 to 10mA ammeter

16.  The purpose of the shunt circuit is to measure
current, I that is n-time multiple of Im
 The number n is called the multiplying factor
and related I and Im as
I=nIm
1
-
n
R
I
nI
R
I
R
m
m
m
m
m
sh




17. Example 2:
A 100μA meter movement with an internal
resistance of 800Ω is used in a 0 to 100mA
ammeter. Find the value of the multiplying
factor and the required shunt
resistance.

18.  Limitation  only works well on a single-
range ammeter
 To overcome this limitation, Ayrton shunt is
introduced

19.  More suitable design for a
multiple-range ammeter
 Also, it can be used with a
wide range of meter
movements
 The individual resistance
value of the shunts are
calculated by starting with
the most sensitive range
towards the least sensitive
range

20.  In this figure, the most sensitive
range is the 1A range
 The least sensitive range is the
10A range
 When the meter is connected to
the most sensitive range, total
shunt resistance is
 Rsh can also be calculated using
Rsh = Ra + Rb + Rc
1
n
R
R m
sh


* In this case, I is equal to 1A
*

21.  In this figure, Rb+Rc is
parallel with Rm+Ra
 Voltage across parallel
branch must be equal
 Rearranging the equation
gives
V Rb +Rc = V Ra +Rm
(Rb+Rc)(I2-Im)=Im(Ra+Rm) 2
)
(
)
(
2




I
R
R
I
R
R m
sh
m
c
b

22. 2
)
(
)
( 


 c
b
sh
a R
R
R
R
)
(
)
(
3



I
R
R
I
R m
sh
m
c
)
(

 a
sh
b R
R
R

23. Example 3:
Compute the value of the shunt resistors for the
circuit shown below

24.  The basic D’Arsonval meter movement can be
converted to a DC voltmeter by connecting a
multiplier in series with the meter movement
 Rs extends the voltage range and limit current
through D’Arsonval meter movement to a
maximum full scale deflection
Rs

25.  To find the value of Rs, the sensitivity, S of the
meter movement must be determined
 The sensitivity is determined by taking the
reciprocal of the full-scale deflection current
 To calculate the value of the multiplier for
voltage ranges greater than 1V;
volt
ohms
ohms
volt
V
I
y
Sensitivit
fs





1
amperes
1
)
/
(
1
Rs = S x Range – Internal Resistance

26. Example 4:
Calculate the sensitivity of a 100μA meter
movement which is to be used as a DC voltmeter

27. Example 5:
Calculate the value of the multiplier resistance
on the 50V range of a dc voltmeter that used a
500μA meter movement with an internal r
esistance of 1kΩ

28. Example 6:
Calculate the value of the multiplier resistance
for the multiple ranges DC voltmeter circuit

29. Example 7:
Calculate the value of the multiplier resistor for
the multiple range DC voltmeter circuit shown

30.  When a voltmeter is used to measure the voltage
across a circuit component, the circuit itself is
parallel with the circuit component in the
voltmeter
 The combination of two parallel resistors is less
than any of the two resistor value.
 Therefore:
- The voltage across the component is less when
the voltmeter is connected
- The decrease of voltage is known as voltmeter
loading
- The resulting error is known as loading error

31. Example 8:
Two different voltmeter
is used to measure the
voltage across resistor RB
in the figure. Calculate:
(a) VRB without meter connected
(b) VRB when meter A is used
(c) VRB when meter B is used
(d) Error in voltmeter reading
Meter A: S=1kΩ/V, Rm=0.2k Ω,
range=10V
Meter B: S=20kΩ/V, Rm=1.5k Ω,
range=10V

32. Example 9:
Find the voltage reading and
the percentage of error of
each reading obtained with a
voltmeter on
(a) Its 3V range
(b) Its 10V range
(c) Its 30V range
When connected across RB.
Instrument has 20kΩ/V
sensitivity

33.  A series circuit is
constructed if points X
and Y are connected
 The magnitude of the
current is limited by the
resistors RZ and Rm
 By connecting X and Y
the circuit will be
shorted and RZ will be
adjusted to obtain full
scale deflection of the
meter movement

34.  The amplitude of the
current through the
meter movement can be
determined as
 When measuring
unknown resistor, RX the
circuit current will be
m
z
f s
R
R
E
I


x
m
z R
R
R
E
I




35.  The amplitude of the
current through the
meter movement can be
determined as
 When measuring
unknown resistor, RX the
circuit current will be
m
z
f s
R
R
E
I


x
m
z R
R
R
E
I



* Current I is less than Ifs because of the additional resistance RX

36.  The ratio of the full-scale deflection current Ifs is
equal to the ratio of the circuit resistance and may
be expressed as
x
m
z
m
z
m
z
x
m
z
fs R
R
R
R
R
)
R
R
/(
E
)
R
R
R
/(
E
I
I
P










37. Example 10:
An ohmmeter uses a 1.5V battery and a basic 50μA
movement. The internal resistance is 1kΩ. Calculate
(a) The value of Rz required
(b) The value of Rx that would cause half-scale
deflection in the circuit

38. Example 11:
An ohmmeter is designed around a 1mA meter
movement and a 1.5V call. If the cell voltage decays to
1.3V because of aging, calculate the resulting error at
midrange on the ohmmeter scale

39.  Ohmmeters are usually nonlinear due to,
 to high internal resistance
 however, at half scale the value of Rx is equal to
the total internal resistance, Rm of an ohmmeter
 A variable resistor may be applied to the ohmmeter
probes and set the value required for half-scale
deflection of the pointer in order to mark the scale.

41. AC
METERS

42.  AC meters
 Half-wave rectification
 Full-wave rectification
 Electrodynamometer

43.  Use to measure AC current or voltage
 By far, the widely used meter movement is the
D’Arsonval meter movement
 However, it cannot measure AC current or
voltage directly
 Some modification is required to use the
D’Arsonval meter movement with AC meter:
1) Half-wave rectification
2) Full-wave rectification
 A rectifier is a circuit which converts AC input to
DC output

44.  During each “positive” half-cycle of the AC sine
wave, the diode is forward-biased and current
flow through the diode
 During each “negative” half-cycle, the diode is
reverse-biased and no current flow through the
diode
 Because only one-half of the input waveform
reaches the output, it is very inefficient if used
for power transfer

45.  It converts the whole of the input waveform to
one of constant polarity (+ or -) at its output
 Four diodes (usually in a bridge configuration) is
required for full-wave rectification

46.  A type of AC meter
 It is a current sensitive device
 Able to handle more current than the
D’Arsonval meter movement could handle
without shunt
 A single coil movement could be used to
measure DC / AC current or voltage

47.  It consists of a fixed coil that is divided into two
equal halves, separated by a movable coil
 It has a very low sensitivity (approximately 20 –
100Ω/V)

48. Example 12:
An electrodynamometer movement that has a
full-scale deflection current rating of 10mA is
to be used in a voltmeter circuit. Calculate the
value of the multiplier for a 10V range if
Rm=50Ω

49. Example 13:
An electrodynamometer movement with a full-
scale deflection current rating of 10mA is to be
used as a 1A ammeter. If the resistance of the
moving coil is 40Ω. What is the value of the
shunt?