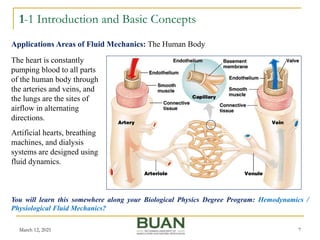
This document provides an overview of fluid mechanics concepts including:
- The definition of a fluid and differences between solids and fluids
- Key terminology like stress, shear stress, and boundary layers
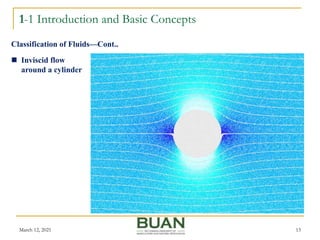
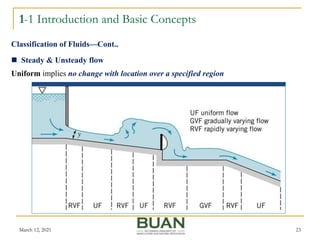
- Classifications of fluid flows such as internal vs. external, viscous vs. inviscid, and compressible vs. incompressible
- The no-slip condition and its implications for fluid behavior near surfaces