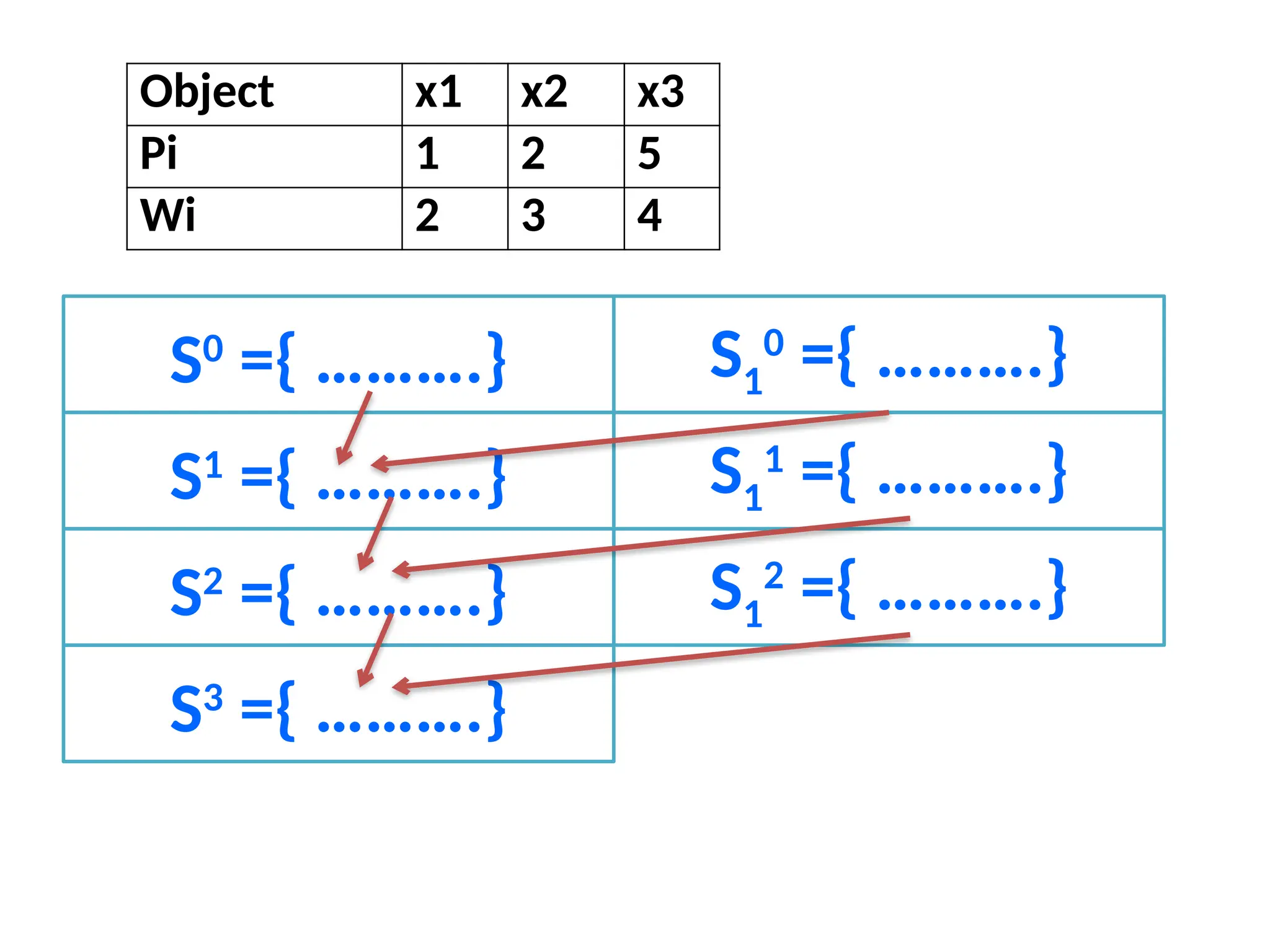
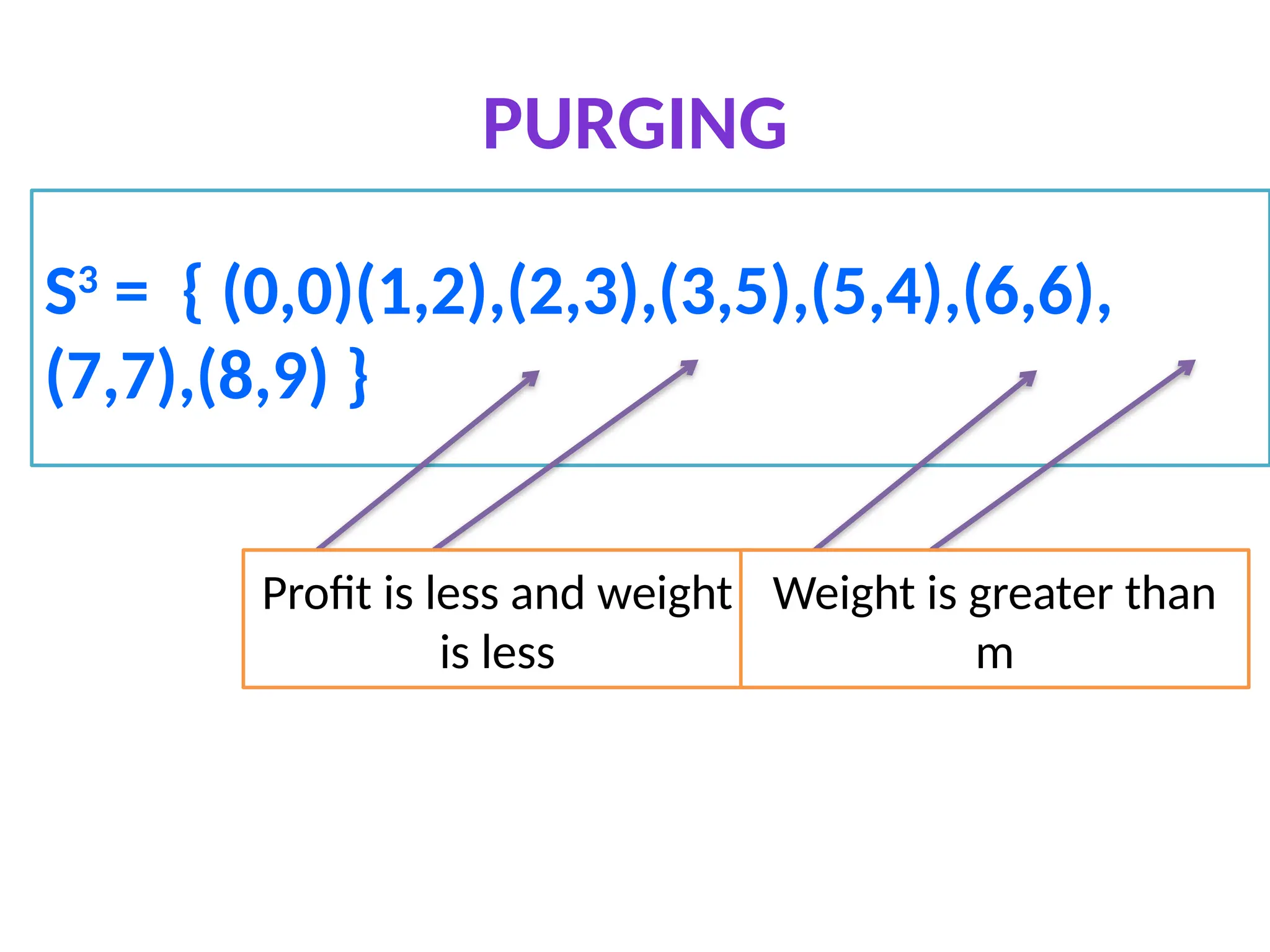
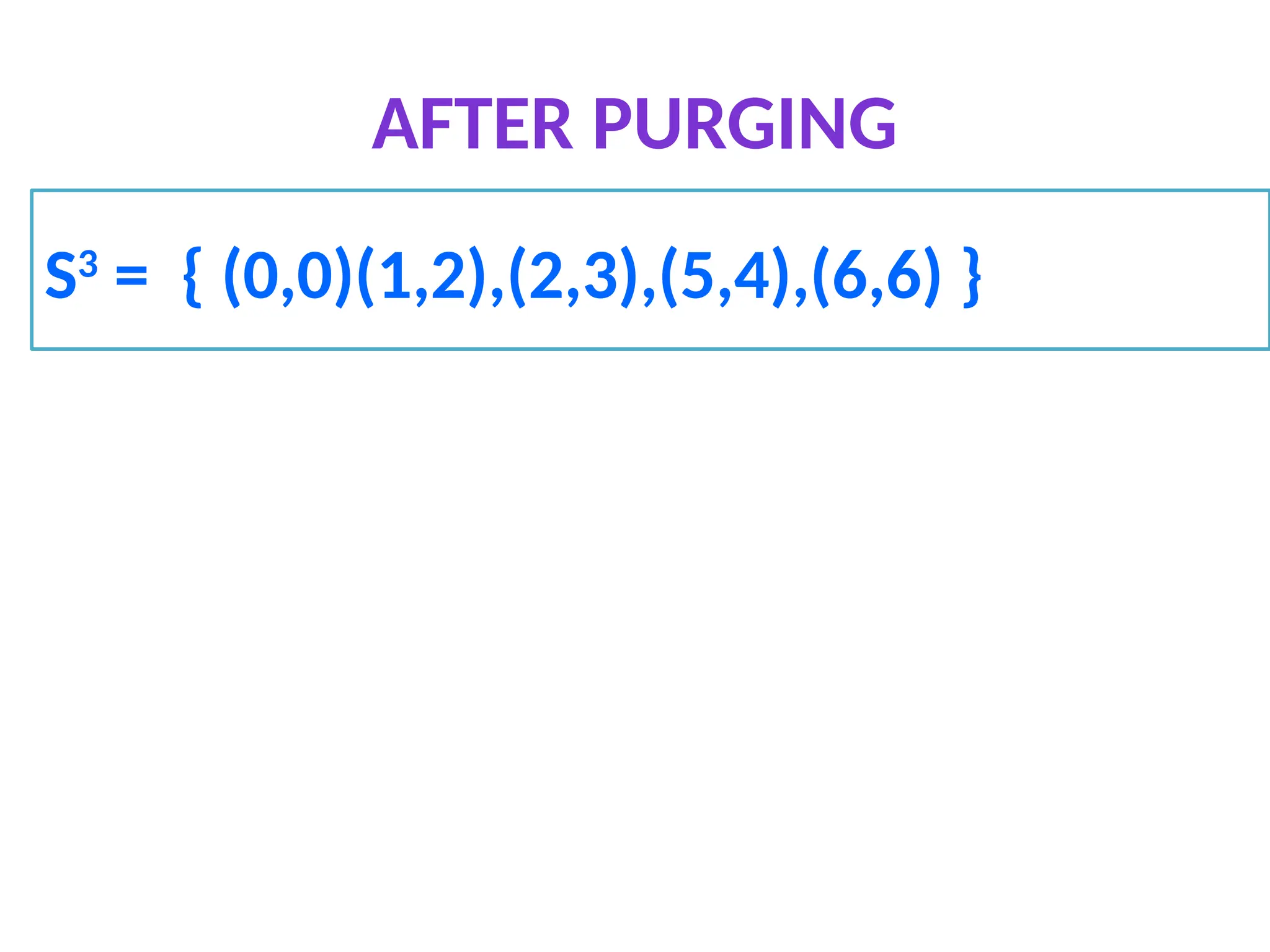
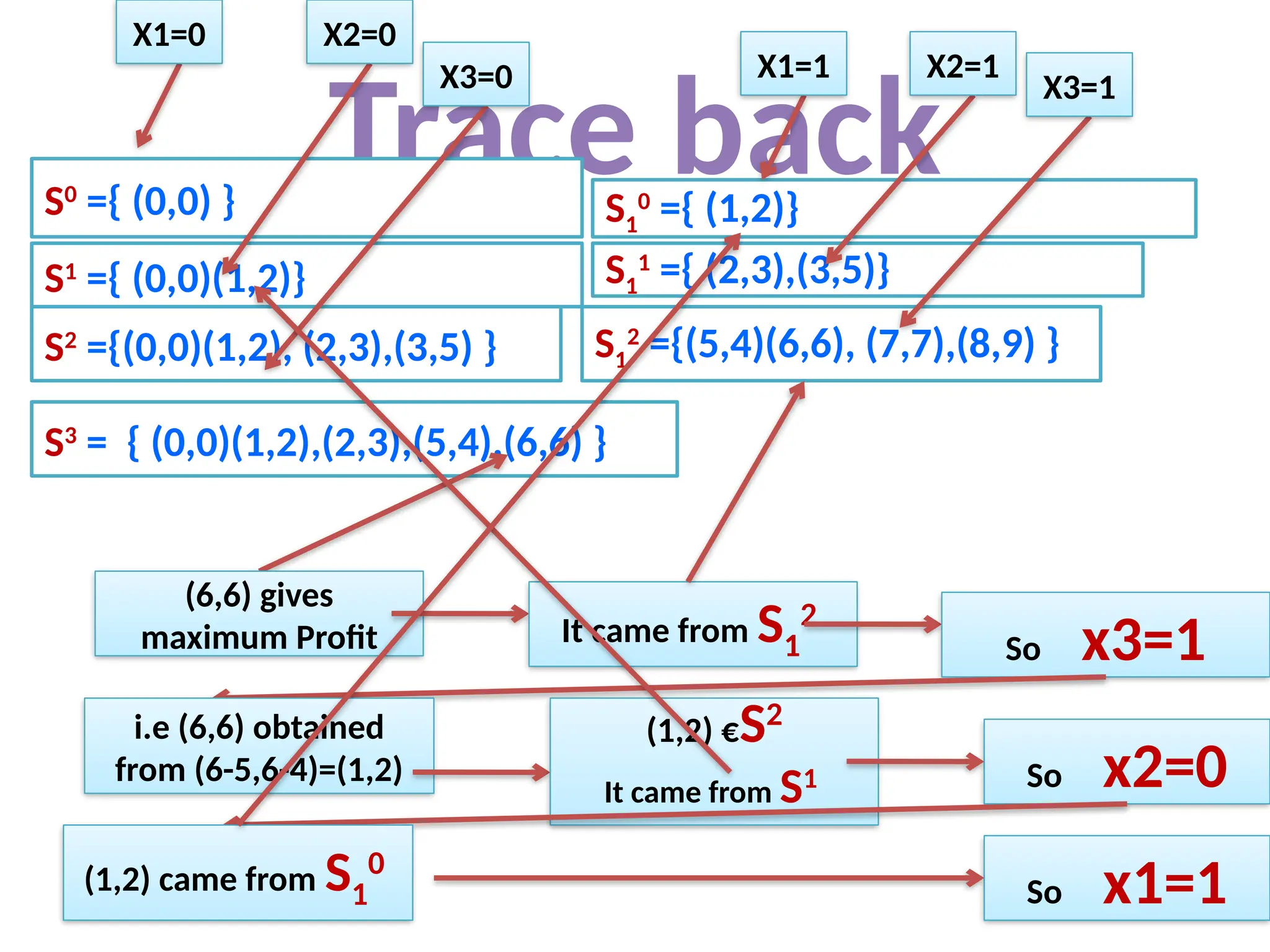
The document discusses the 0/1 knapsack problem, which involves selecting a subset of objects with given weights and profits to maximize total profit without exceeding a specified capacity. It outlines a dynamic programming approach to solve the problem efficiently by maintaining pairs of profit and weight and employing a strategy of merging and purging these pairs to avoid redundancies. An example illustrates the application of this method, ultimately leading to a solution vector that indicates the selected objects.

1. 0/1 knapsack using DP

2. 0/1 Knapsack Problem
• We are given a knapsack of capacity m and a set of n objects numbered
1,2,…,n. Each object i has weight wi and profit pi.
• Let x = [x1, x2,…, xn] be a solution vector in which xi = 0 if object i is not in
the knapsack, and xi = 1 if it is in the knapsack.
• The goal is to find a subset of objects to put into the knapsack so that
(that is, the objects fit into the knapsack) and
is maximized (that is, the profit is maximized).

3. 0/1 Knapsack Problem
• The naive method is to consider all 2n
possible subsets of
the n objects and choose the one that fits into the
knapsack and maximizes the profit.
• Let F[i,x] be the maximum profit for a knapsack of capacity
x using only objects {1,2,…,i}. The DP formulation is:

4. S1
i
={(P,W)|(P-pi+1 ,W- wi+1 ) € Si }
we can compute Si+1
by merging and purging
the pairs in Si
and S1
i
Note :S0
={(0,0)}

5. Purging -
• If Si+1
contains 2 pairs (Pj,Wj) and (Pk,Wk)
with property that
Pj <= Pk and
Wj >= Wk
• and weight exceeds capacity of bag

6. Example
• n=3 m=6
(w1,w2,w3)=(2,3,4)
(p1,p2,p3)= (1,2,5)

7. Object x1 x2 x3
Pi 1 2 5
Wi 2 3 4
S0
={ ……….}
S1
={ ……….}
S2
={ ……….}
S3
={ ……….}
S1
0
={ ……….}
S1
1
={ ……….}
S1
2
={ ……….}

8. Object x1 x2 x3
Pi 1 2 5
Wi 2 3 4
S0
={ ……….}
S0
={ (0,0) } S1
0
={ (1,2)}
S1
={ ……….}
S1
={ (0,0)(1,2)} S1
1
={ (2,3),(3,5)}
x2
2
3
x1
1
2

9. Object x1 x2 x3
Pi 1 2 5
Wi 2 3 4
S0
={ ……….}
S1
={ (0,0)(1,2)} S1
1
={ (2,3),(3,5)}
x2
2
3
x1
1
2
S2
={ ……….}
S2
={(0,0)(1,2), (2,3),(3,5) }
x3
5
4
S1
2
={(5,4)(6,6), (7,7),(8,9) }

10. Object x1 x2 x3
Pi 1 2 5
Wi 2 3 4
S0
={ ……….}
x2
2
3
x1
1
2
S2
= {(0,0)(1,2), (2,3),(3,5) }
x3
5
4
S1
2
={(5,4)(6,6), (7,7),(8,9) }
S3
={ ……….}
S3
= { (0,0)(1,2), (2,3),(3,5),(5,4),(6,6),
(7,7),(8,9) }

11. PURGING
S3
= { (0,0)(1,2),(2,3),(3,5),(5,4),(6,6),
(7,7),(8,9) }
Profit is less and weight
is less
Weight is greater than
m

12. AFTER PURGING
S3
= { (0,0)(1,2),(2,3),(5,4),(6,6) }

13. Trace back
S0
={ (0,0) } S1
0
={ (1,2)}
S1
={ (0,0)(1,2)} S1
1
={ (2,3),(3,5)}
S2
={(0,0)(1,2), (2,3),(3,5) } S1
2
={(5,4)(6,6), (7,7),(8,9) }
S3
= { (0,0)(1,2),(2,3),(5,4),(6,6) }
X1=0
X1=1
X2=0
X2=1
X3=0 X3=1
(6,6) gives
maximum Profit It came from S1
2
So x3=1
i.e (6,6) obtained
from (6-5,6-4)=(1,2)
(1,2) €S2
It came from S1 So x2=0
(1,2) came from S1
0
So x1=1

14. Solution is
(x1,x2,x3) = (1,0,1)

15. Algorithm