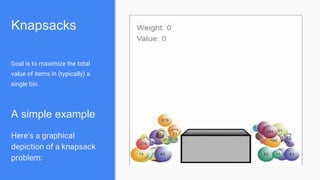
The document discusses the bin-packing problem, particularly focusing on the knapsack variant where the objective is to maximize the value of packed items within a specified weight limit. It presents an example of the knapsack problem, illustrating the use of a formula for optimal packing combinations, as well as the implementation of a Python algorithm to solve it. The content highlights the practical application of operational research in decision-making processes through advanced analytical methods.

1. Bin-Packing / Knapsacks
Problem
(Combinatorial Optimization Project)

2. How we use the Knapsacks for
Bin-packing?

3. Intro of Bin-Packing
Bin packing is the problem of trying to find a set of objects to pack into
containers (or bins). The objects have weights (or volumes), and each
container has a capacity, which is the total weight (or volume) the container
can hold.
One of the most common bin packing problems is knapsacks.

4. Knapsacks
Goal is to maximize the total
value of items in (typically) a
single bin.
A simple example
Here's a graphical
depiction of a knapsack
problem:

5. Knapsack Problem Example
Truck – 10t capacity
Optimum cargo combination:
•Item 1: $5 (3t)
•Item 2: $7 (4t)
•Item 3: $8 (5t)

6. Knapsack Problem
Output function f(i,w)
Optimum output of a combination of items 1 to i with a
cumulated weight of w or less.
•Item 1: x1=$5 ; w1=3t
•Item 2: x2=$7 ; w2=4t
•Item 3: x3=$8 ; w3=5t

7. Knapsack Problem
Output function f(i,w)
f(i,w)=Max[ xi + f(i,w-wi) ; f(i-1,w) ]
ONE Item i + optimum
combination of weight w-wi
NO Item i + optimum
combination items 1 to i-
1

8. Knapsack Problem
Table
1 2 3 4 5 6 7 8 9 10
1
2
3
w
i f(i,w)

9. Knapsack Problem
Table
1 2 3 4 5 6 7 8 9 10
1
2
3
w
i
Using only item 1

10. Knapsack Problem
Table
1 2 3 4 5 6 7 8 9 10
1
2
3
w
i
Using only item 1 & 2

11. Knapsack Problem
Table
1 2 3 4 5 6 7 8 9 10
1
2
3
w
i
Using items 1, 2 & 3

12. Knapsack Problem
Table
1 2 3 4 5 6 7 8 9 10
1 0 0 5 5 5 10
2
3
w
2 items n°1
2 w1 = 6
0 items n°1 1 items n°1
w1 = 3

13. Knapsack Problem
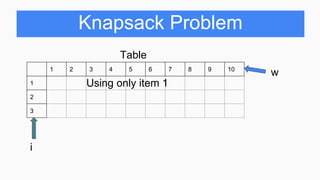
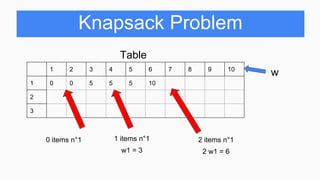
Table
1 2 3 4 5 6 7 8 9 10
1 0 0 5 5 5 10 10 10 15 15
2 0 0 5 7
3
w-w2 =
5 - 4 = 1
f(i,w)=Max[ xi + f(i,w-wi) ; f(i-1,w) ]
+ x2(=7)

14. Knapsack Problem
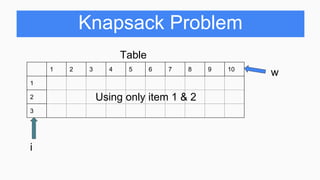
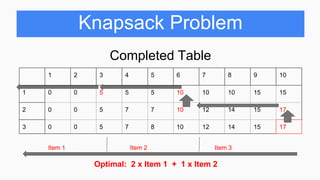
Table
1 2 3 4 5 6 7 8 9 10
1 0 0 5 5 5 10 10 10 15 15
2 0 0 5 7 7
3
f(i,w)=Max[ xi + f(i,w-wi) ; f(i-1,w) ]
+ x2(=7)

15. Knapsack Problem
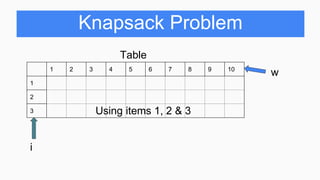
Table
1 2 3 4 5 6 7 8 9 10
1 0 0 5 5 5 10 10 10 15 15
2 0 0 5 7 7
3
w-w2 =
6 - 4 = 2
f(i,w)=Max[ xi + f(i,w-wi) ; f(i-1,w) ]
+ x2(=7)

16. Knapsack Problem
Table
1 2 3 4 5 6 7 8 9 10
1 0 0 5 5 5 10 10 10 15 15
2 0 0 5 7 7 10
3
f(i,w)=Max[ xi + f(i,w-wi) ; f(i-1,w) ]
+ x2(=7)

17. Knapsack Problem
1 2 3 4 5 6 7 8 9 10
1 0 0 5 5 5 10 10 10 15 15
2 0 0 5 7 7 10 12 14 15 17
3 0 0 5 7 8 10 12 14 15 17
Completed Table
Optimal: 2 x Item 1 + 1 x Item 2
Item 1 Item 2 Item 3

18. Python code for Knapsack problem
from ortools.algorithms import pywrapknapsack_solver
def main():
# Create the solver.
solver = pywrapknapsack_solver.KnapsackSolver(
pywrapknapsack_solver.KnapsackSolver.
KNAPSACK_MULTIDIMENSION_BRANCH_AND_BOUND_SOLVER,
'test')
values = [360, 83, 59, 130, 431, 67, 230, 52, 93,
125, 670, 892, 600, 38, 48, 147, 78, 256,
63, 17, 120, 164, 432, 35, 92, 110, 22,
42, 50, 323, 514, 28, 87, 73, 78, 15,
26, 78, 210, 36, 85, 189, 274, 43, 33,
10, 19, 389, 276, 312]

19. weights = [[7, 0, 30, 22, 80, 94, 11, 81, 70,
64, 59, 18, 0, 36, 3, 8, 15, 42,
9, 0, 42, 47, 52, 32, 26, 48, 55,
6, 29, 84, 2, 4, 18, 56, 7, 29,
93, 44, 71, 3, 86, 66, 31, 65, 0,
79, 20, 65, 52, 13]]
capacities = [850]
solver.Init(values, weights, capacities)
computed_value = solver.Solve()
packed_items = [x for x in range(0, len(weights[0]))
if solver.BestSolutionContains(x)]
packed_weights = [weights[0][i] for i in packed_items]
total_weight= sum(packed_weights)

20. Print the output
or result.
print("Packed items: ", packed_items)
print("Packed weights: ", packed_weights)
print("Total value: ", computed_value)
print("Total weight: ", total_weight)
if __name__ == '__main__':
main()
Packed items: [0, 1, 3, 4, 6, 10, 11, 12, 14, 15,
16, 17, 18, 19, 21, 22, 24, 27, 28, 29, 30, 31,
32, 34, 38, 39, 41, 42, 44, 47, 48, 49]
Packed weights: [7, 0, 22, 80, 11, 59, 18, 0, 3,
8, 15, 42, 9, 0, 47, 52, 26, 6, 29, 84, 2, 4, 18, 7,
71, 3, 66, 31, 0, 65, 52, 13]
Total value: 7534
Total weight: 850
Output of the python
code

21. “Operational research (in British usage), is a
discipline that deals with the application of advanced
analytical methods to help make better decisions.”

22. Thanks!
GAURAV DUBEY(2017msbda003)
MSc. CS(BIG DATA ANALYTICS)
Central University of
Rajasthan
Bandarsindri, Kishangarh, Ajmer,
pin : 305817.
2017msbda003@curaj.ac.in