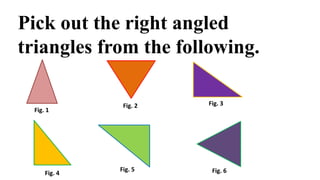
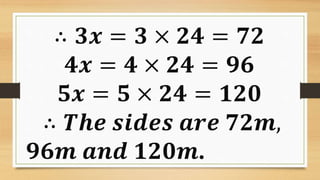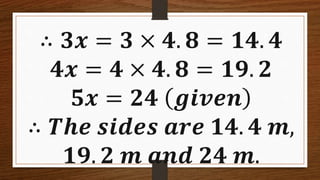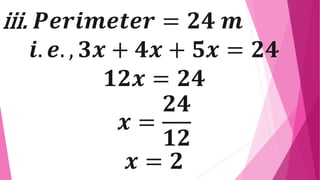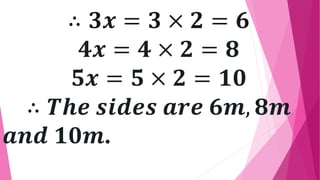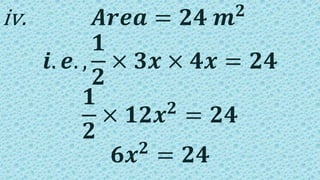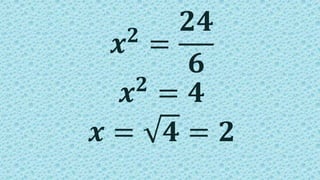This document provides instructions and solutions for problems involving right triangles. It begins by asking the reader to identify right triangles from various figures and to name the components of a right triangle - the perpendicular sides and hypotenuse. It then presents four problems involving right triangles where the ratio of perpendicular sides is given as 3:4 and additional information is provided to determine the lengths of the sides. The solutions show setting up and solving equations using the Pythagorean theorem and properties of the triangles to find the side lengths of each triangle.

1. Prepared by:
SABJA RAJAN
MOUNT TABOR TRAINING
COLLEGE
PATHANAPURAM

2. Pick out the right angled
triangles from the following.
Fig. 1
Fig. 2 Fig. 3
Fig. 4
Fig. 5 Fig. 6

3. A right angled triangle is
shown below. Answer the
questions that follows.C
A B

4. 1)Name the perpendicular sides of the
triangle shown?
2)What do we call the third side (BC) of
the triangle shown?
3)What is the relation connecting
perpendicular sides and hypotenuse of
a right angled triangle?
4)What is the area of a triangle?
5)What is the perimeter of a triangle?

5. Here comes the
problem of the
day…

6. There are four right triangles, the ratio of
perpendicular sides being 3:4 in each. One
more fact about each is given below. Find the
lengths of the sides of each triangle.
i.The difference in the lengths of the
perpendicular sides is 24 metres.
ii.The hypotenuse is 24 metres.
iii.The perimeter is 24 metres.
iv.The area is 24 square metres.

7. Let’s have a look into the
solutions…

8. Ratio of the perpendicular
sides=3:4
Let the perpendicular sides be
3𝑥 and 4𝑥.
By using Pythagoras Theorem,
𝐻𝑦𝑝𝑜𝑡𝑒𝑛𝑢𝑠𝑒2
= (3𝑥)2
+(4𝑥)2

9. 𝐻𝑦𝑝𝑜𝑡𝑒𝑛𝑢𝑠𝑒2
= 9𝑥2
+ 16𝑥2
= 25𝑥2
∴ 𝐻𝑦𝑝𝑜𝑡𝑒𝑛𝑢𝑠𝑒 = 25𝑥2
= 5𝑥

10. i. Difference in lengths of
perpendicular
sides=24metres
∴ 𝟒𝒙 − 𝟑𝒙 = 𝟐𝟒
𝒙 = 𝟐𝟒

11. ∴ 𝟑𝒙 = 𝟑 × 𝟐𝟒 = 𝟕𝟐
𝟒𝒙 = 𝟒 × 𝟐𝟒 = 𝟗𝟔
𝟓𝒙 = 𝟓 × 𝟐𝟒 = 𝟏𝟐𝟎
∴ 𝑻𝒉𝒆 𝒔𝒊𝒅𝒆𝒔 𝒂𝒓𝒆 𝟕𝟐𝒎,
𝟗𝟔𝒎 𝒂𝒏𝒅 𝟏𝟐𝟎𝒎.

12. ii. 𝑯𝒚𝒑𝒐𝒕𝒆𝒏𝒖𝒔𝒆 = 𝟐𝟒 𝒎
𝒊. 𝒆. , 𝟓𝒙 = 𝟐𝟒
𝒙 =
𝟐𝟒
𝟓
𝒙 = 𝟒. 𝟖

13. ∴ 𝟑𝒙 = 𝟑 × 𝟒. 𝟖 = 𝟏𝟒. 𝟒
𝟒𝒙 = 𝟒 × 𝟒. 𝟖 = 𝟏𝟗. 𝟐
𝟓𝒙 = 𝟐𝟒 𝒈𝒊𝒗𝒆𝒏
∴ 𝑻𝒉𝒆 𝒔𝒊𝒅𝒆𝒔 𝒂𝒓𝒆 𝟏𝟒. 𝟒 𝒎,
𝟏𝟗. 𝟐 𝒎 𝒂𝒏𝒅 𝟐𝟒 𝒎.

14. iii. 𝑷𝒆𝒓𝒊𝒎𝒆𝒕𝒆𝒓 = 𝟐𝟒 𝒎
𝒊. 𝒆. , 𝟑𝒙 + 𝟒𝒙 + 𝟓𝒙 = 𝟐𝟒
𝟏𝟐𝒙 = 𝟐𝟒
𝒙 =
𝟐𝟒
𝟏𝟐
𝒙 = 𝟐

15. ∴ 𝟑𝒙 = 𝟑 × 𝟐 = 𝟔
𝟒𝒙 = 𝟒 × 𝟐 = 𝟖
𝟓𝒙 = 𝟓 × 𝟐 = 𝟏𝟎
∴ 𝑻𝒉𝒆 𝒔𝒊𝒅𝒆𝒔 𝒂𝒓𝒆 𝟔𝒎, 𝟖𝒎
𝒂𝒏𝒅 𝟏𝟎𝒎.

16. iv. 𝑨𝒓𝒆𝒂 = 𝟐𝟒 𝒎 𝟐
𝒊. 𝒆. ,
𝟏
𝟐
× 𝟑𝒙 × 𝟒𝒙 = 𝟐𝟒
𝟏
𝟐
× 𝟏𝟐𝒙 𝟐
= 𝟐𝟒
𝟔𝒙 𝟐
= 𝟐𝟒

17. 𝒙 𝟐
=
𝟐𝟒
𝟔
𝒙 𝟐
= 𝟒
𝒙 = 𝟒 = 𝟐

18. ∴ 𝟑𝒙 = 𝟑 × 𝟐 = 𝟔
𝟒𝒙 = 𝟒 × 𝟐 = 𝟖
𝟓𝒙 = 𝟓 × 𝟐 = 𝟏𝟎
∴ 𝑻𝒉𝒆 𝒔𝒊𝒅𝒆𝒔 𝒂𝒓𝒆 𝟔𝒎, 𝟖𝒎
𝒂𝒏𝒅 𝟏𝟎𝒎.

19. THANK YOU…