The document discusses a color halftoning technique called parawacs, which uses a deterministic algorithm to improve the printing process by managing colors and minimizing moiré effects. It highlights the challenges of traditional halftoning and presents the benefits of this method, especially in contexts like security printing and watermarking. Ultimately, the parawacs approach offers greater control and flexibility over final print patterns compared to conventional methods.

1. CIC24, November 7 – 11, 2016, San Diego, California
PARAWACS:
color halftoning
with a single selector matrix
Peter Morovič, Ján Morovič,
Jay Gondek, Matthew Gaubatz,
Robert Ulichney
HP Inc., Spain & USA

2. © Copyright 2016 HP Inc.
PArallel RAndom Weighted Area Coverage Selection

3. © Copyright 2016 HP Inc.
Outline
❖ Background
❖ HANS
❖ PARAWACS
❖ Basic principles
❖ Plane dependence
❖ Security printing
❖ Conclusions

4. © Copyright 2016 HP Inc.
Background
❖ Color and image processing pipeline of printing system needs to answer:
❖ how to adjust colors to capabilities of printing system (color management)
❖ how to combine colorants to match colors (color separation)
❖ how to translate colorant amounts into discrete colorant placement (halftoning)
❖ Traditional picture:
❖ color separation: how much of each colorant to use for each printable color
❖ halftoning: making spatial choices, given colorant amounts
❖ halftoning colorant amounts one by one leads to unwanted interactions
❖ choose halftoning matrices to minimize moiré (e.g., Amidor et al., 1994)
❖ plane-dependency between specific pairs of colorants (e.g., Zhang et al.,
2012).
❖ Color halftoning challenges follow from difficulties of acting on colorant amount
choices
❖ As domain of color separation changes,
so do constraints and opportunities for halftoning
The Emir of Bukhara
1911 color photograph
Sergei Mikhailovich Prokudin-Gorskii

5. © Copyright 2016 HP Inc.
HANS: from colorants to Neugebauer primaries
CMY: 7 degrees of freedom
instead of 3
CMmYKkNnRGB: 1023 DOF
instead of 10
How many pixels of which
composition instead of how
much of which colorant

6. © Copyright 2016 HP Inc.
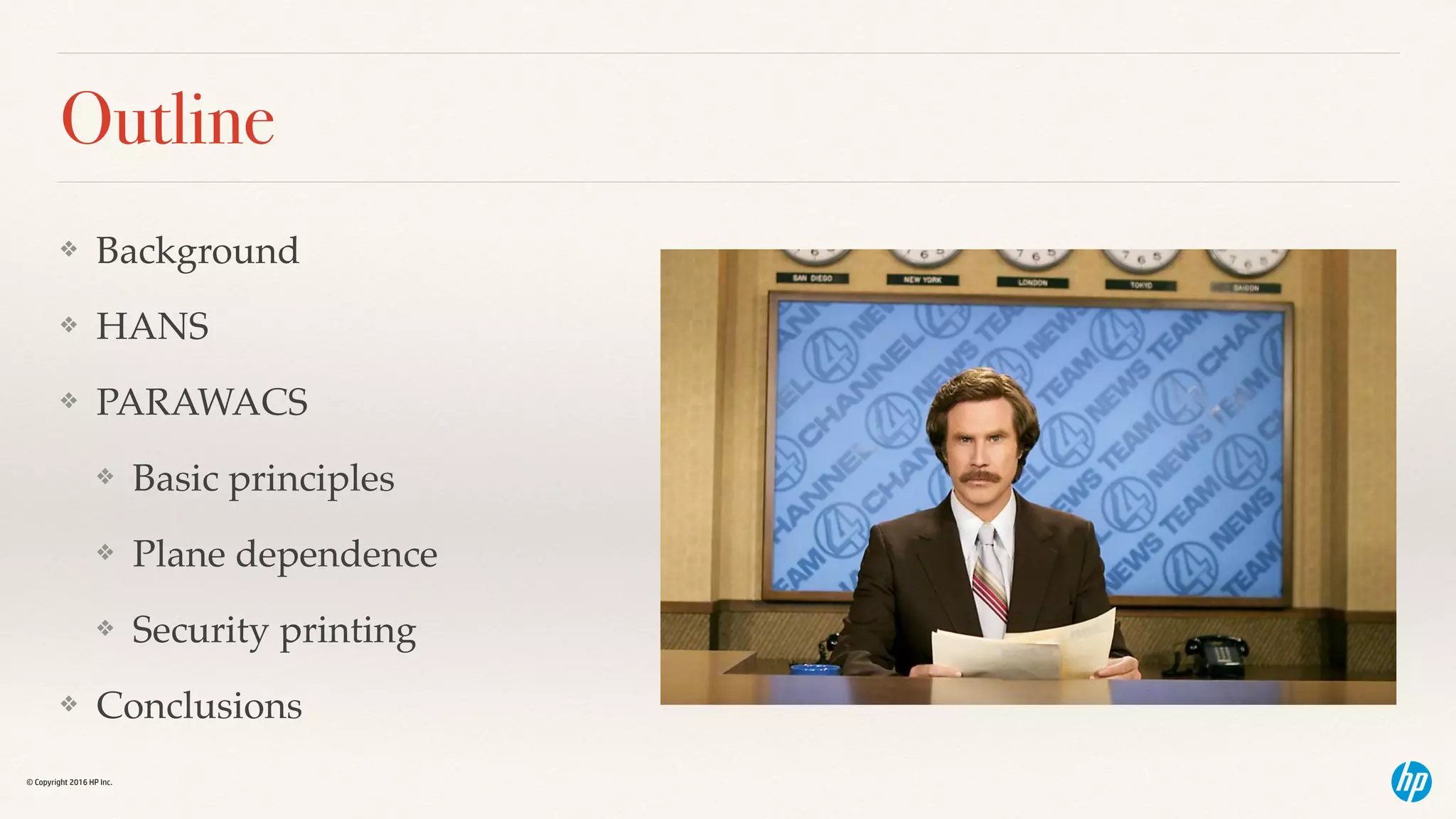
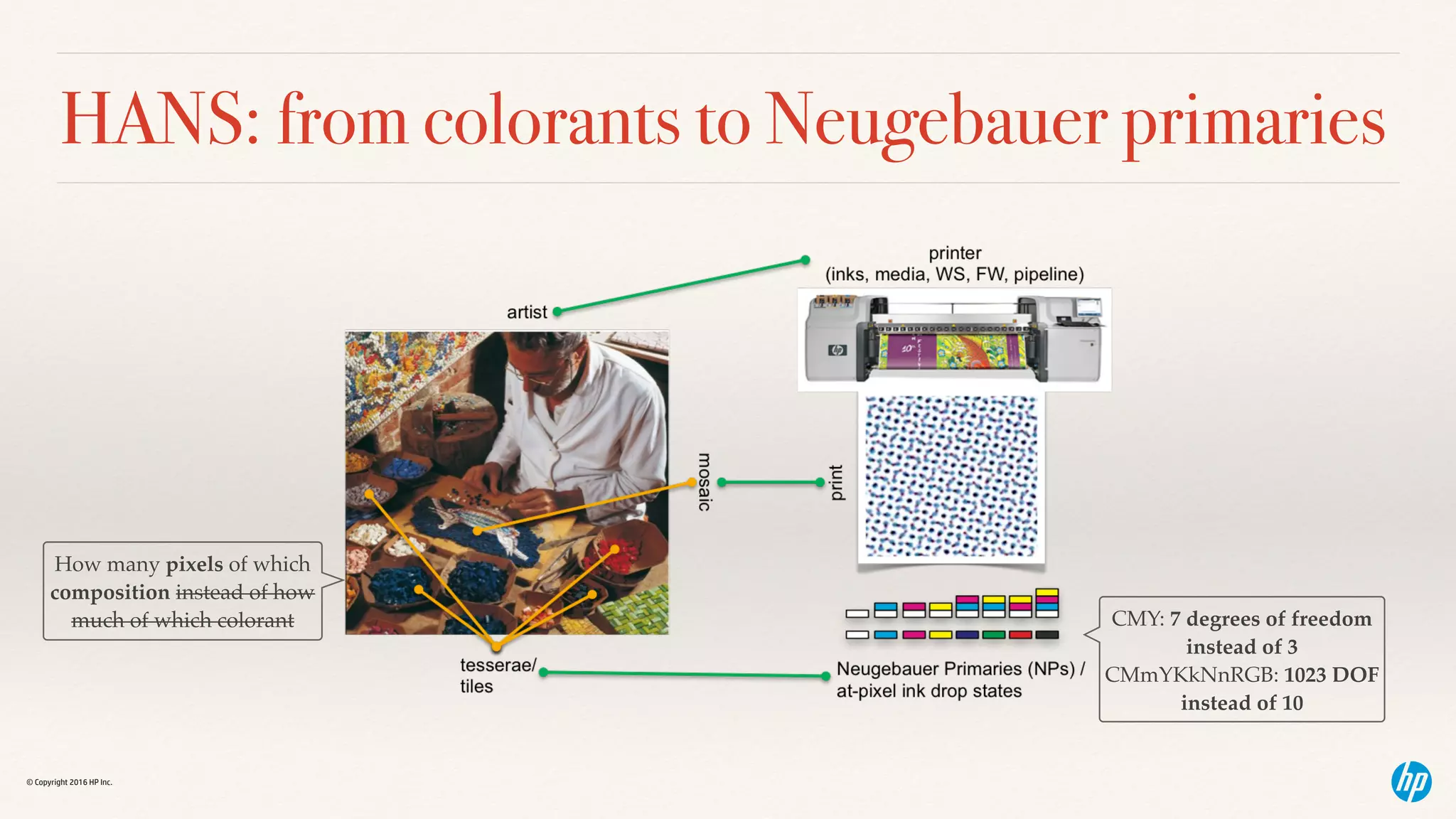
NPacs and their error-diffusion
❖ Neugebauer Primary (NP): composition of single
halftone pixel
❖ e.g., blank, one colorant, several colorants, several
quantities of a single colorant …
❖ Neugebauer Primary area coverage (NPac) vector:
relative area coverages of NPs over some unit area /
probability of encountering given NPs
❖ e.g., [w,C,MY]=[0.6,0.3,0.1]
❖ 60% of some local area left blank
❖ 30% covered by the cyan colorant
❖ 10% contain combination of magenta and yellow
BUT: slow
(not parallelizable)
& has randomness
(variable)

7. © Copyright 2016 HP Inc.
–Johnny Appleseed
“Couldn’t we use matrices for halftoning NPacs?”
How would we
cross-correlate
all those matrices?
Wouldn’t we need
10s/100s/1000s
of matrices?
I didn’t know you guys
worked with Johnny!?

8. © Copyright 2016 HP Inc.
Back to basics: what does H/T need to do for HANS?
❖ Ink-channel and HANS separation both use relative proportions of
addressable channels
❖ BUT: ink-channel quantities underdetermine halftone patterns (one ink
vector → many patterns), while NPacs relate to proportions of at-pixel
device states that have unique statistics
❖ Since area coverages implicitly refer to a unit area, proportions of an
NPac express relative sub-areas that need to be occupied by each NP
❖ Hence, role of halftoning is that
❖ For a sufficiently large area of a constant NPac
❖ Result in placement of individual NPs such that
❖ when counting their frequencies over the area
❖ the original NP area coverages are obtained
❖ Analogous to traditional, ink-channel based separations: ink coverages
specified → halftoning distributes them so that area of constant ink-
channel coverage, once halftoned, results in specified ink amounts

9. © Copyright 2016 HP Inc.
A first, naïve approach
❖ 128 x 128 pixels
❖ NPac: [w, M, C]= [80%, 10%, 10%]
❖ Halftoning by placing NPs
sequentially from top left corner
of unit area
❖ 1638 pixels (10%) each of Magenta
and Cyan
❖ Remaining pixels left blank (80%)
❖ Satisfies constraint of distributing
relative area coverages of NPac
❖ BUT: looks bad!

10. © Copyright 2016 HP Inc.
–Johnny Appleseed
“The likelihood of picking one of the NPs from an NPac
is equal to that NP’s area coverage.”

11. © Copyright 2016 HP Inc.
Sampling a cumulative distribution
❖ If we uniformly randomly sampled locations of
naïve halftone we would have 80% chance of
picking blank location, 10% chance each of
picking cyan or magenta
❖ BUT: an important attribute of halftoning is
missing: a uniform spatial distribution of NPs
❖ Generate uniformly distributed random numbers
& scale them to [0, 100]
❖ Depending on randomly generated value, choose
a different NP, proportionally to its area coverage
❖ To simplify selection, NPac can be expressed
cumulatively:
❖ [w, M, C]=[80%, 10%, 10%] becomes [80%, 90%,
100%]
❖ Defines intervals for each NP:
❖ [0 to 80) → w, [80 to 90) → M and [90 to 100] → C

12. © Copyright 2016 HP Inc.
Basic Algorithm
0
25
50
75
100
CMY CY M Blank
Selector
Value:
75
25
5
Selected
NP:
Blank
M
CMY
Cumulative NPac
PARAWACS operation at [x, y]:NP Coverage
CMY 10%
CY 10%
M 10%
Blank 70%

13. © Copyright 2016 HP Inc.
From on-demand selectors to matrices
❖ Ad-hoc random numbers (and
sequential placement) can be thought
of as selector matrices
❖ uniformly distributed random
numbers → white noise
❖ sequential placement → ~AM line
halftoning
❖ Can be pre-computed using existing
techniques (green noise, blue noise, …)

14. © Copyright 2016 HP Inc.
Blue and green noise
Spatial structure of single
selector matrix is directly
translated into the halftone

15. © Copyright 2016 HP Inc.
All of these have the same NPac!
It’s the exact same pixels, just
differently arranged.
“I'm playing all the right notes,
but not necessarily in the right order.”
Eric Morecambe

16. © Copyright 2016 HP Inc.
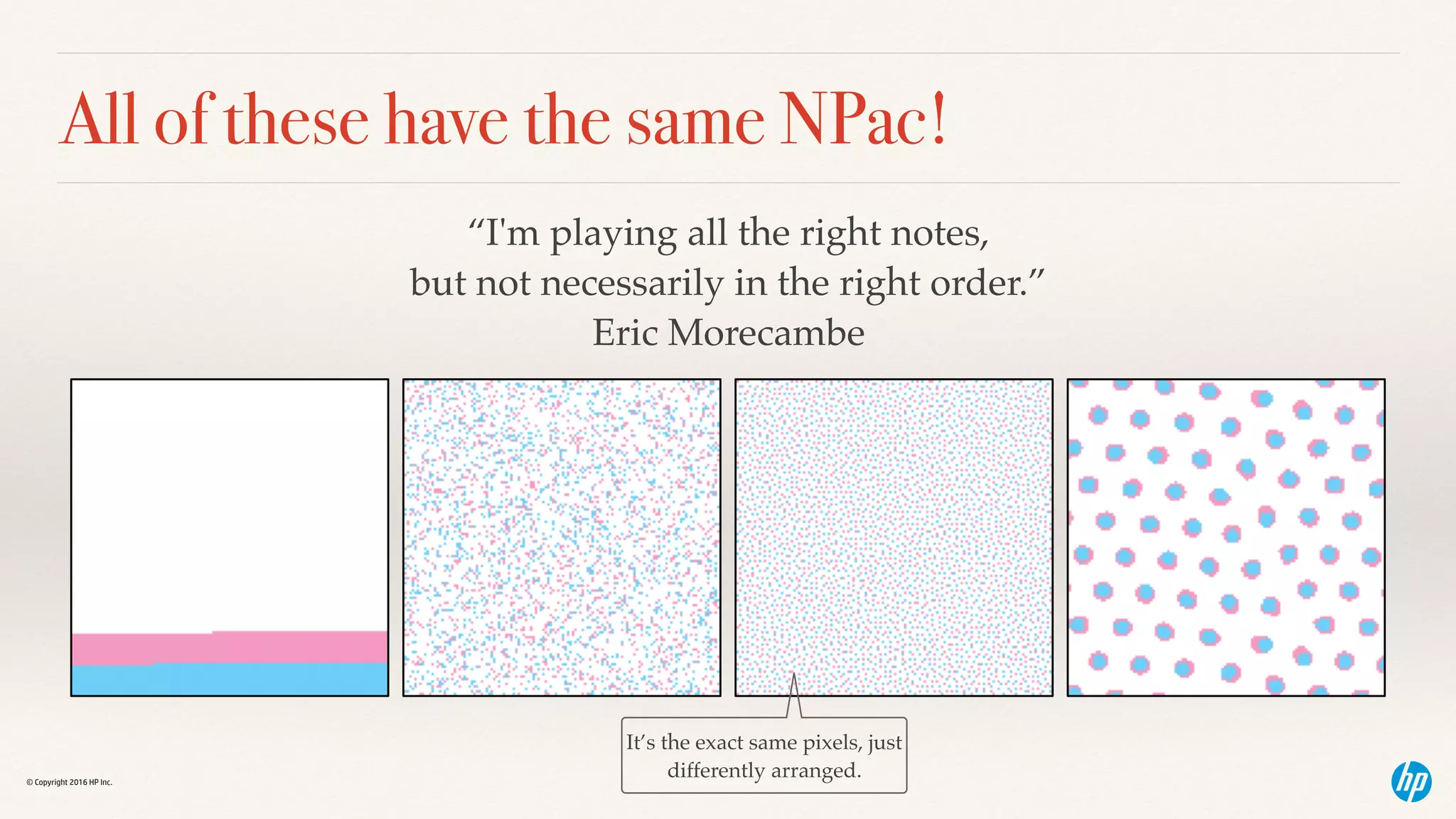
Order! (same NPac, same matrix)
[w, M, C]=[80%, 90%, 100%] [C, M, w]=[10%, 20%, 100%]

17. © Copyright 2016 HP Inc.
Lena!
white blue green

18. © Copyright 2016 HP Inc.
Planedependence
PARAWACS error-diffusion

19. © Copyright 2016 HP Inc.
Security printing
❖ Stegatones replace windows of a halftone
with carefully chosen, rearranged versions
of the contents of the same window
(Ulichney et al. 2010).
❖ For clarity, a simpler modification is used
here, applied directly to the halftone matrix:
values within NxM windows of the halftone
matrix are rearranged into ascending order
❖ Clearly modifies spatial characteristics of
the halftone matrix, without affecting the
frequency of each halftone value
❖ Maintains basic constraint of halftone
matrix and only alters local spatial
arrangement.

20. © Copyright 2016 HP Inc.
Conclusions
❖ Color halftoning impacts many aspects of a print (e.g., grain,
smoothness, color)
❖ A novel, predictable, deterministic algorithm was presented
❖ Shown to give a great degree of control over the final output
patterns
❖ Is well behaved: for different content that shares overall coverage,
halftone pattern is provably constant → well suited for applications
such as security printing, watermarking, data carrying
❖ Existing research into patterns that are visually pleasing or exhibit
particular behavior can be directly applied
❖ PARAWACS is therefore a uniquely flexible
color halftoning approach

21. © Copyright 2016 HP Inc.
Thanks for stopping by!
Tsuyoshi Yamashita
Ron Burns
Utpal Sarkar
Jordi Arnabat
Annarosa Multari
Africa Real