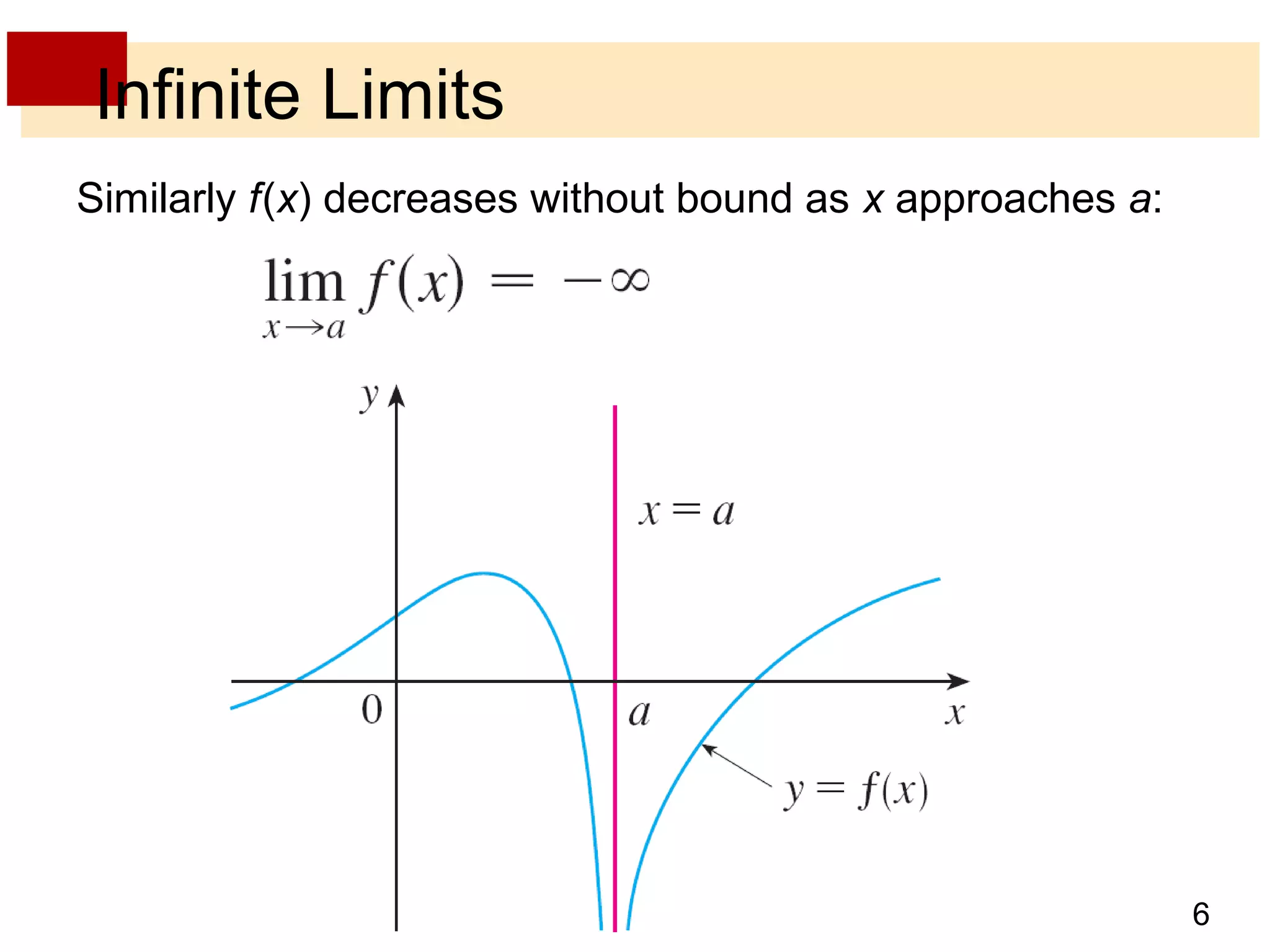
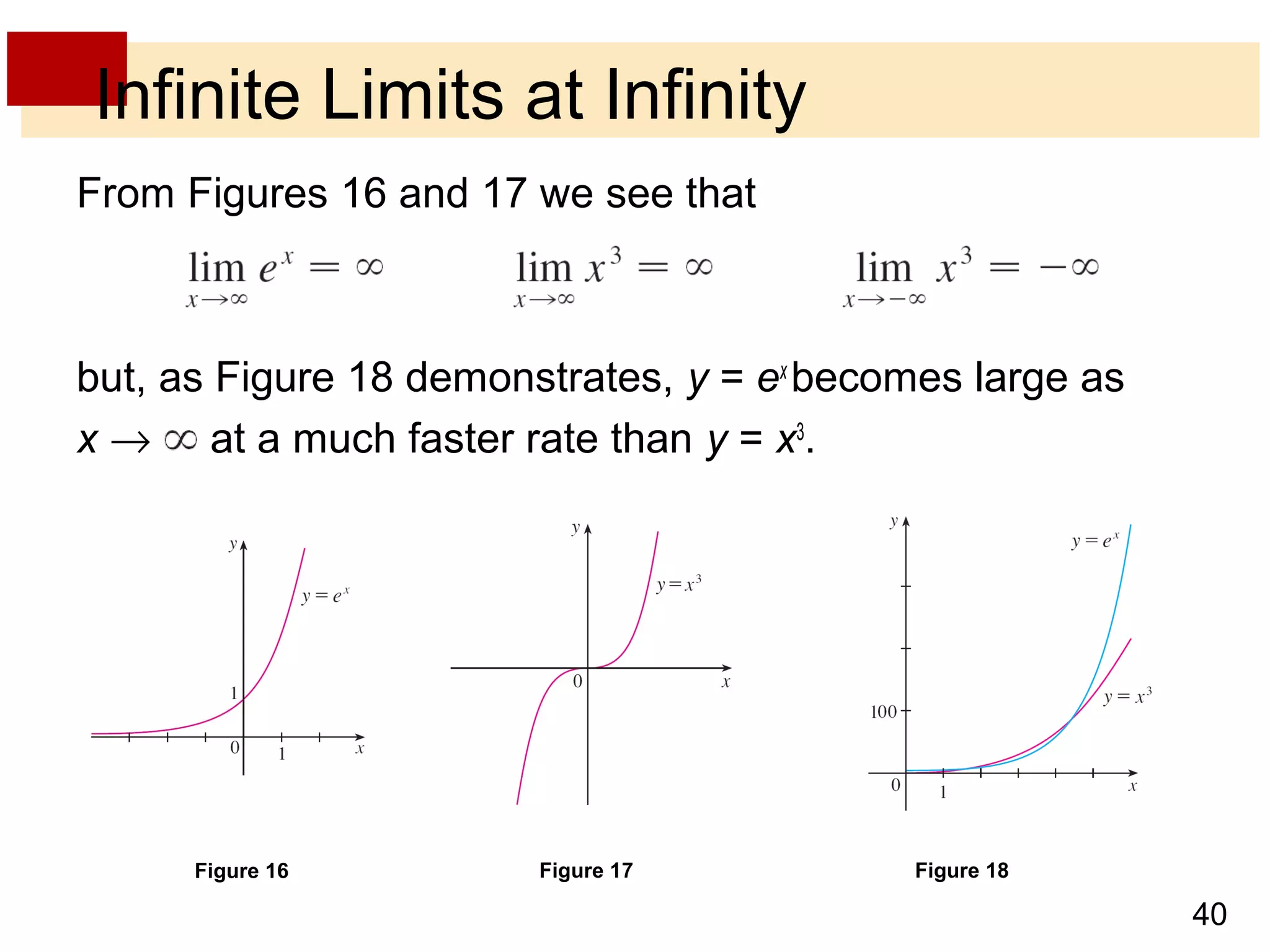
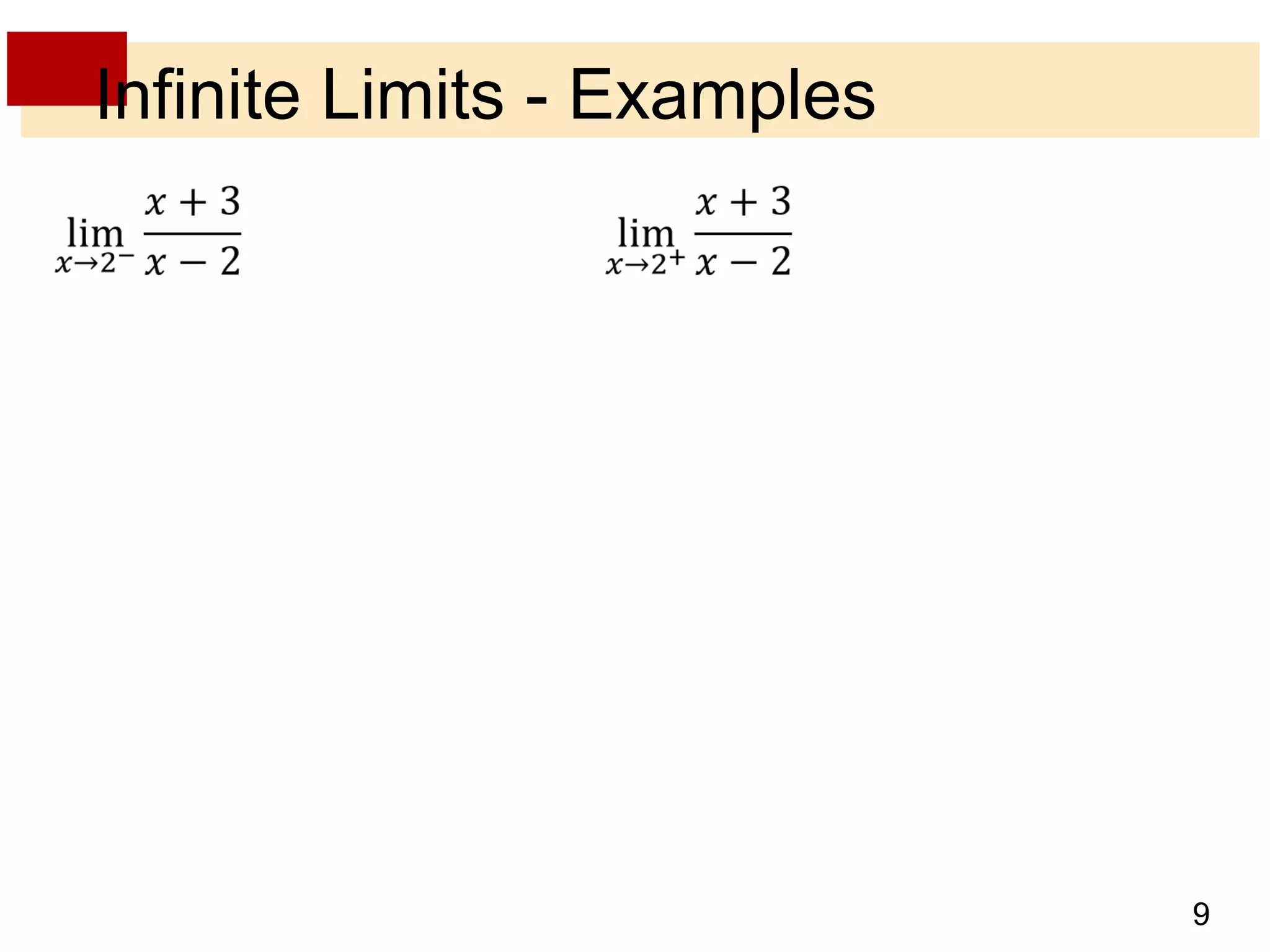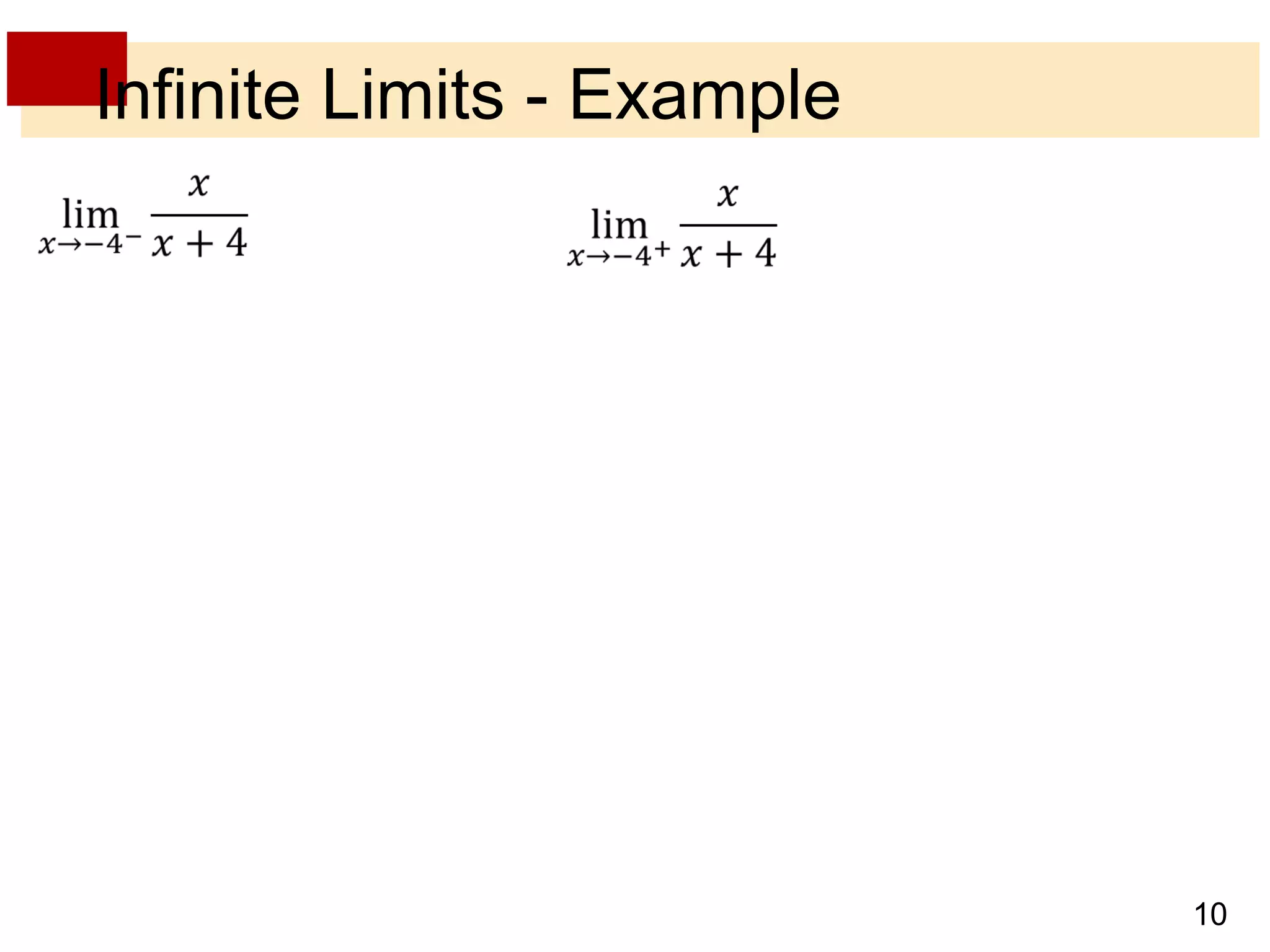This document discusses limits involving infinity, including infinite limits, limits at infinity, and asymptotes. It provides examples and explanations of the following key points:
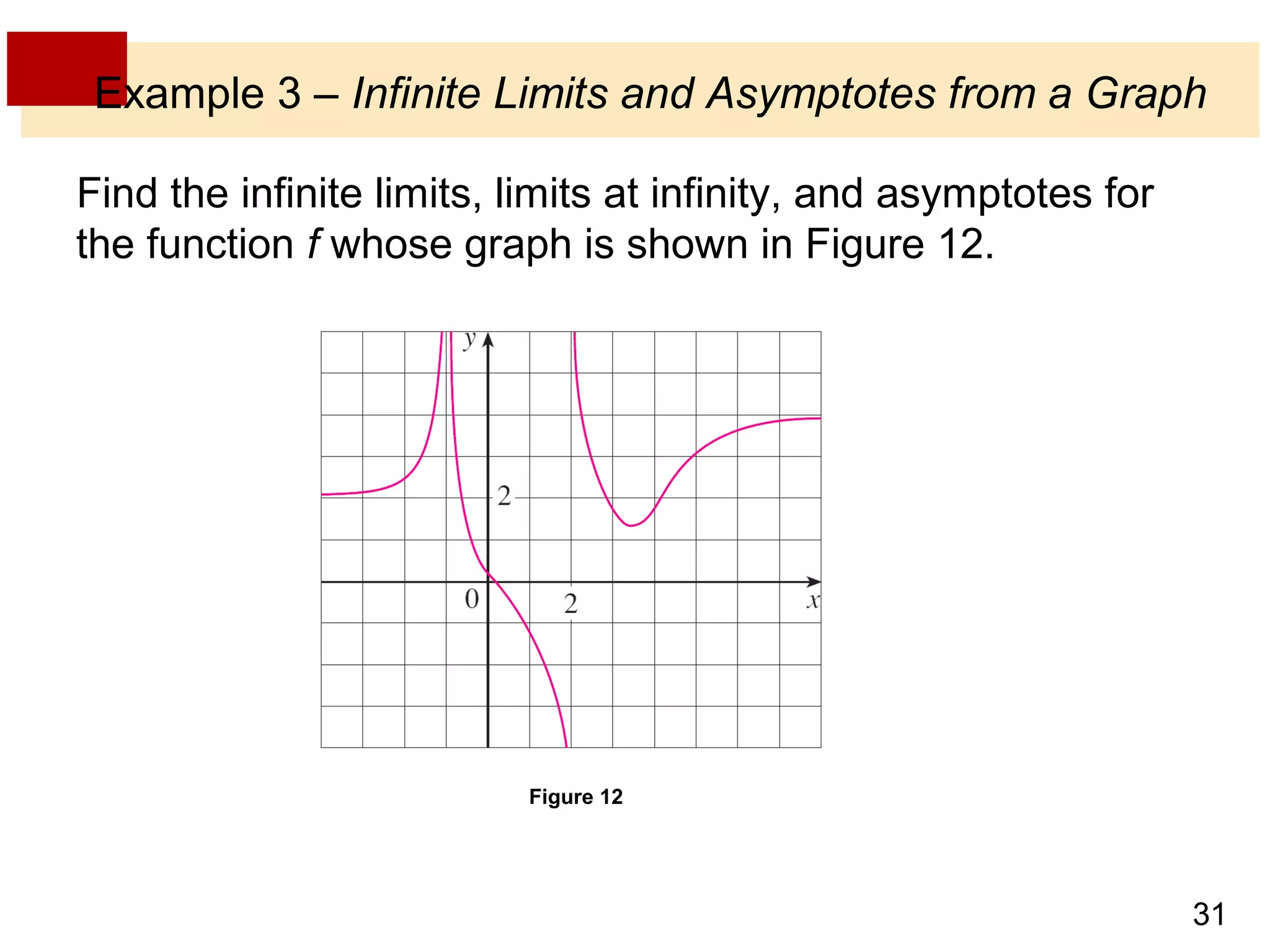
- Infinite limits are indicated with symbols like limx→a f(x) = ∞ to show that f(x) increases without bound as x approaches a.
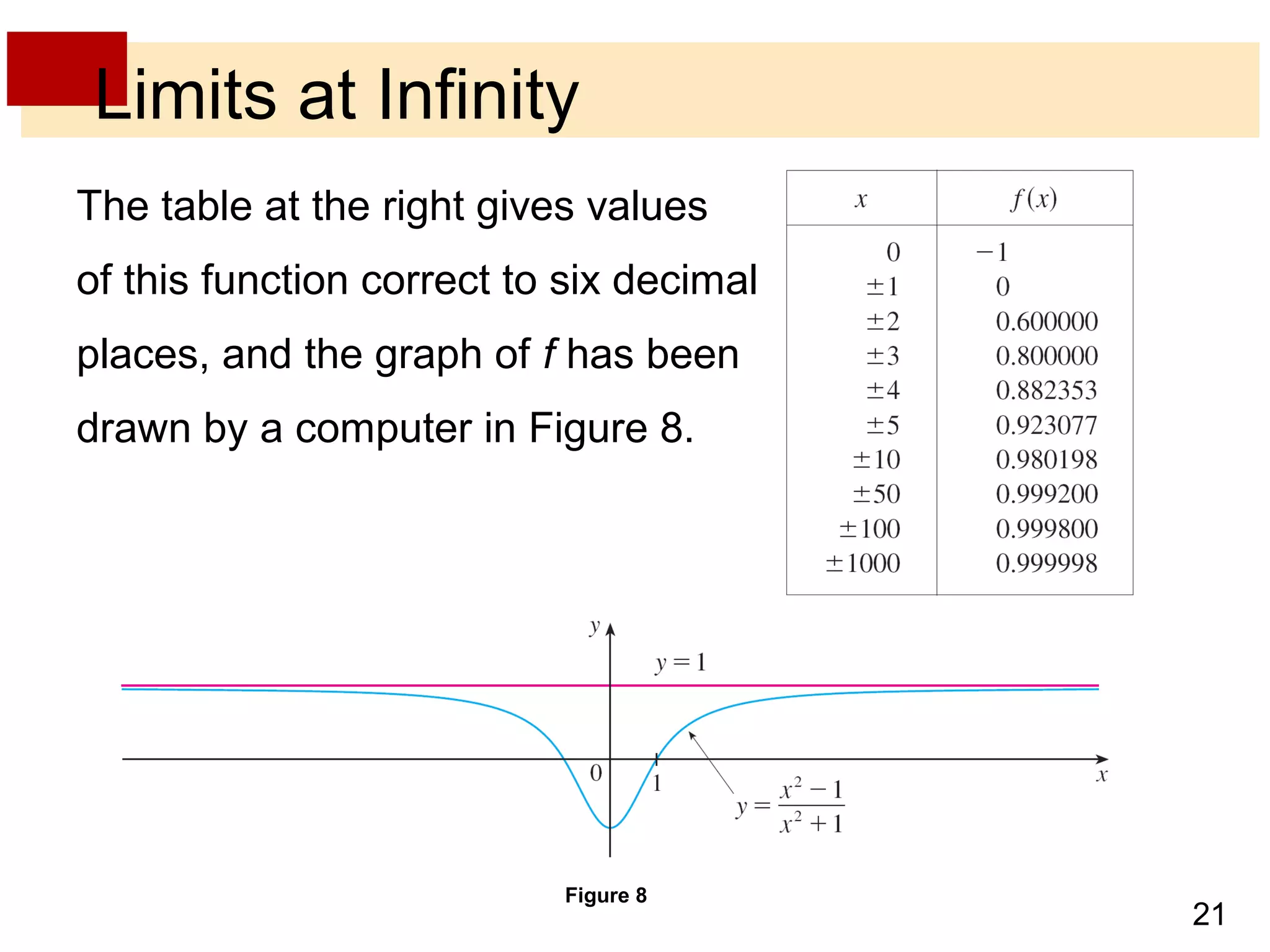
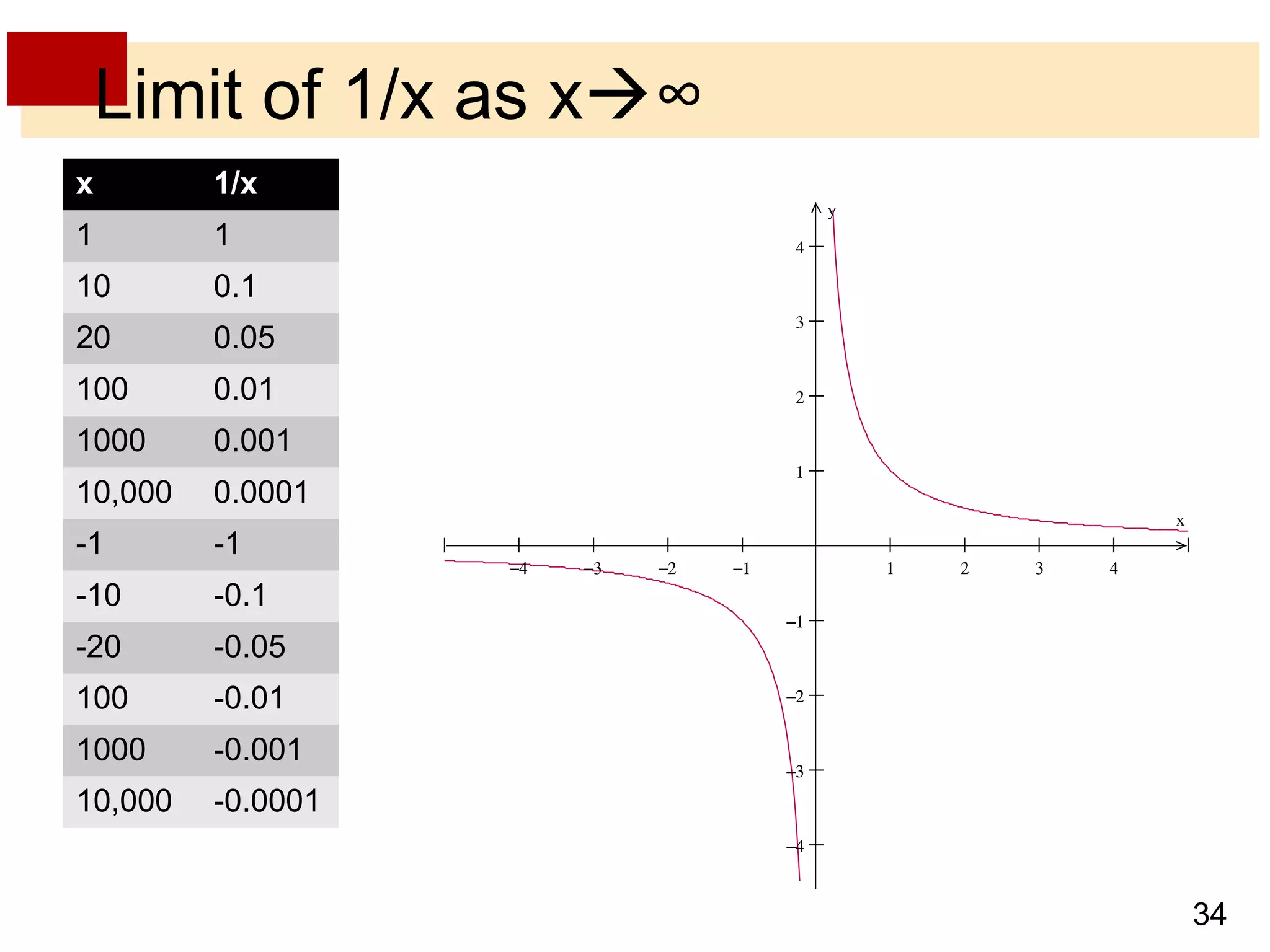
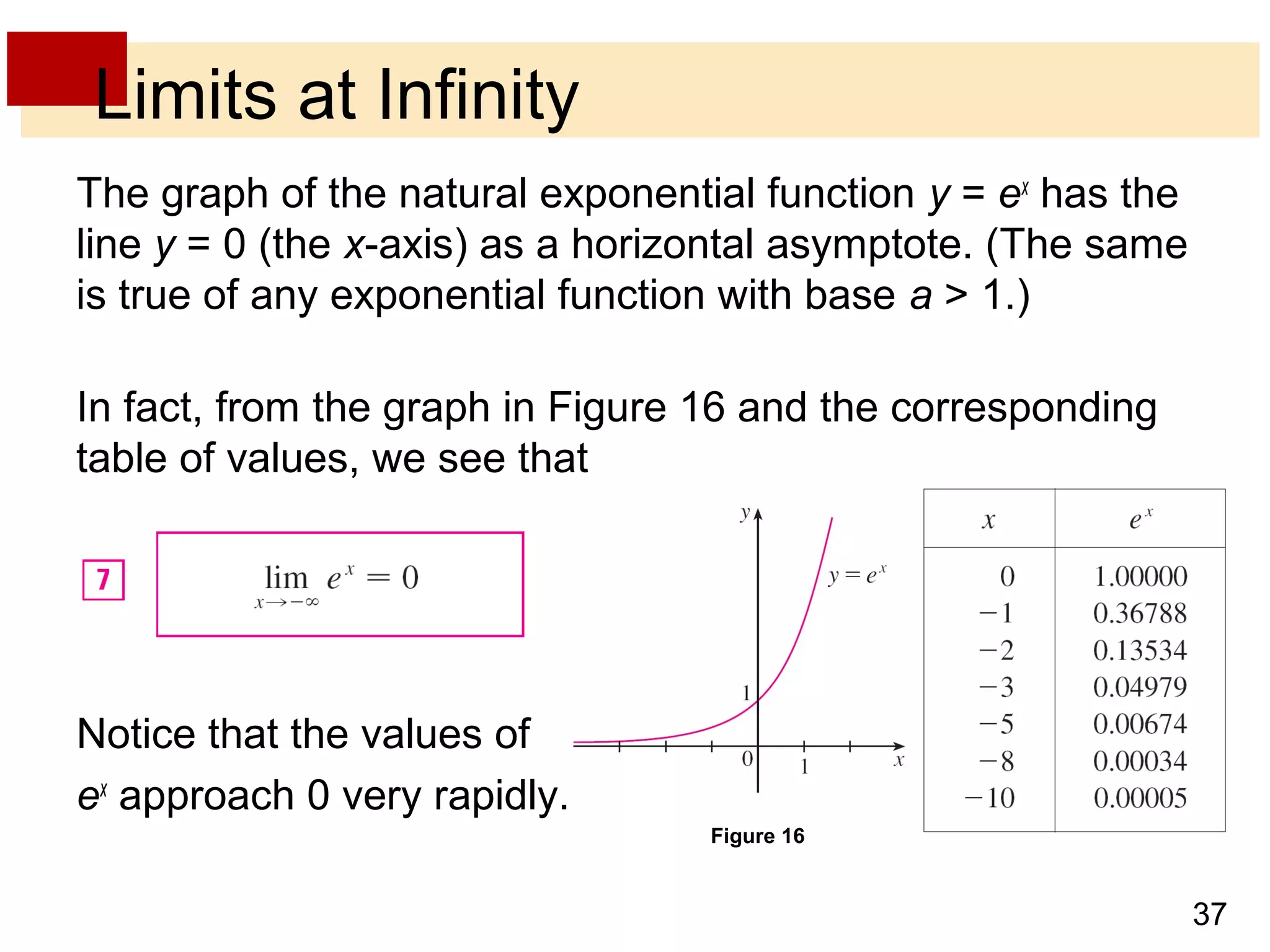
- Limits at infinity use symbols like limx→∞ f(x) = L to show that f(x) approaches the number L as x increases without bound.
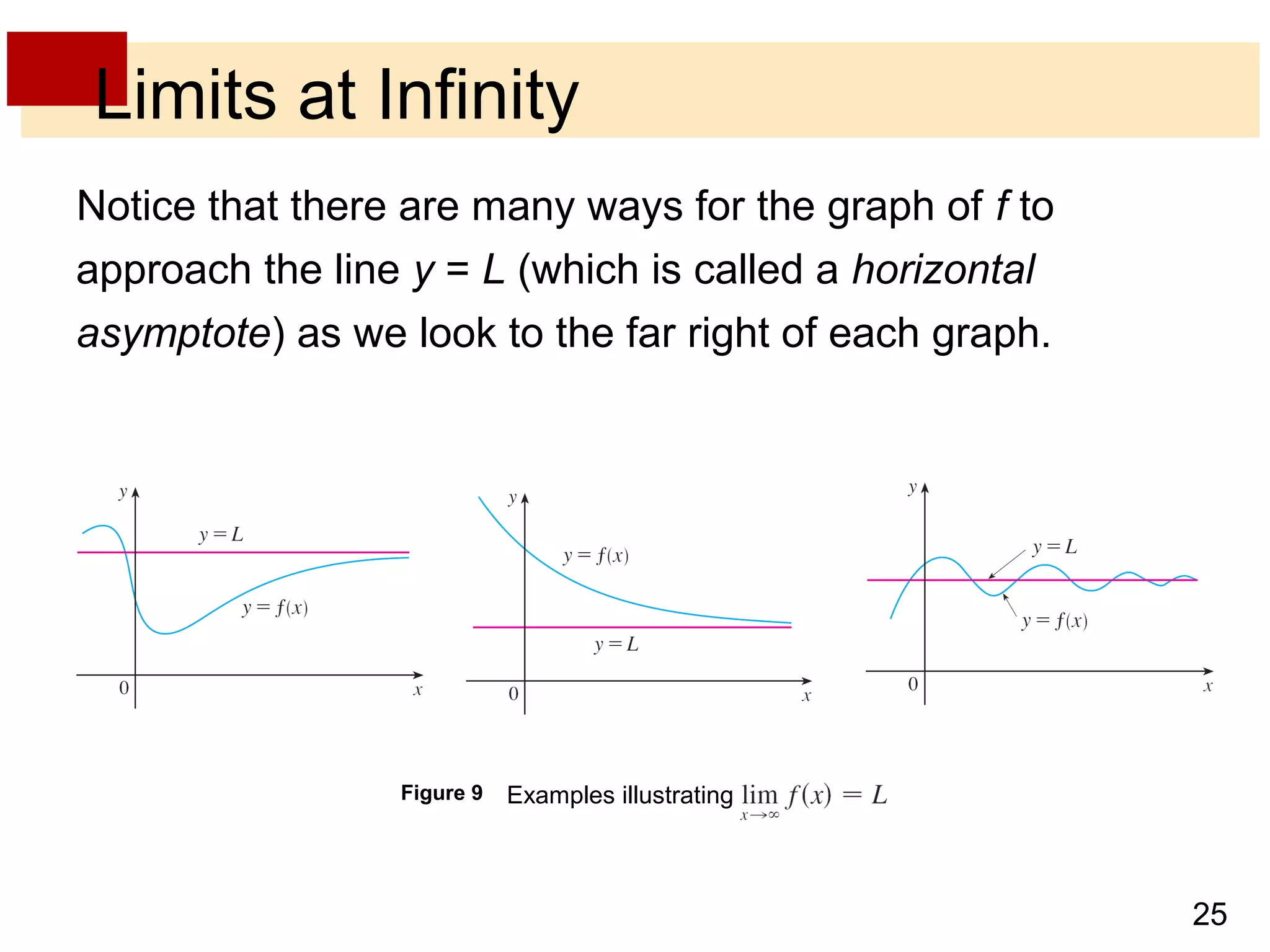
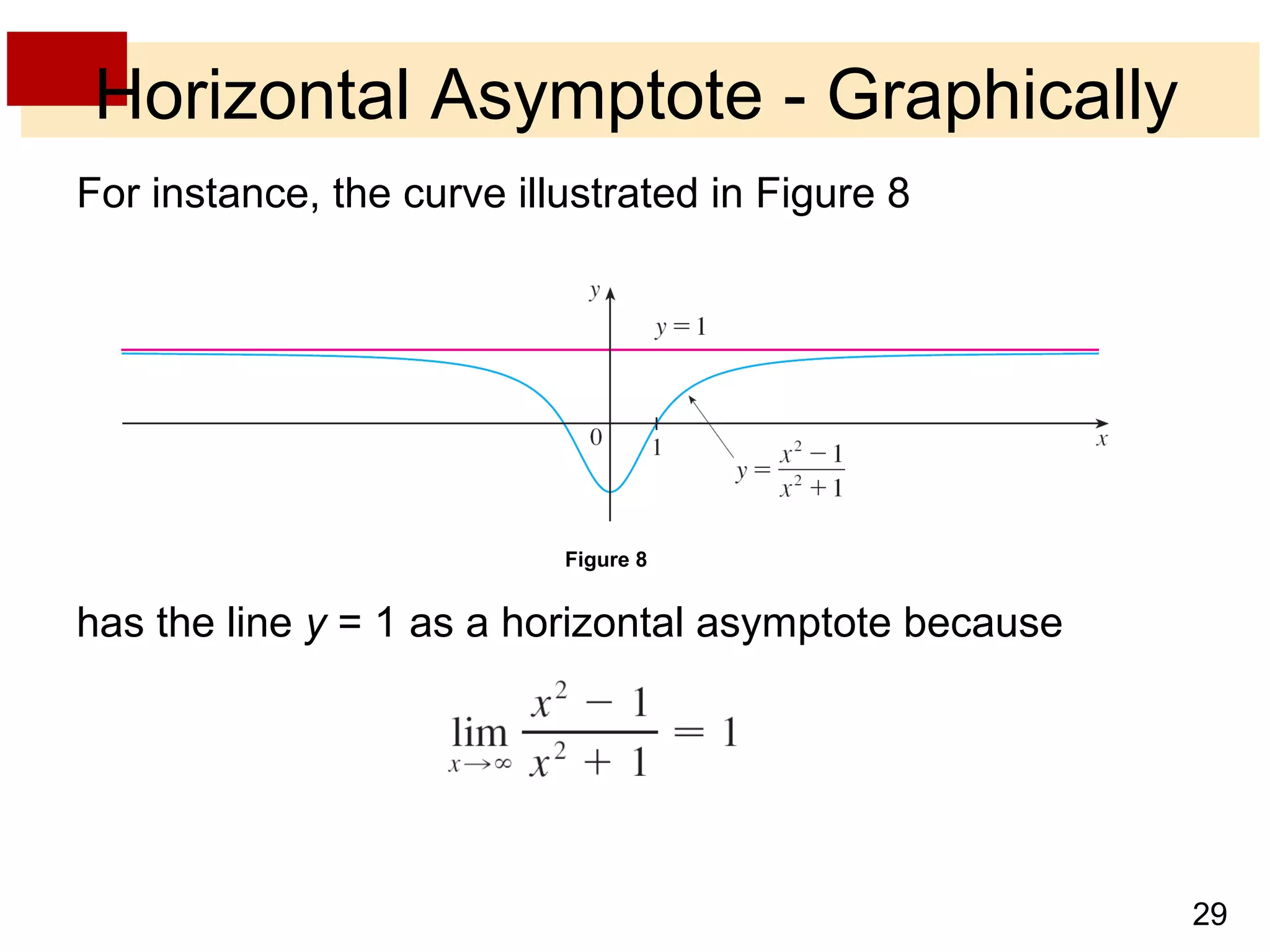
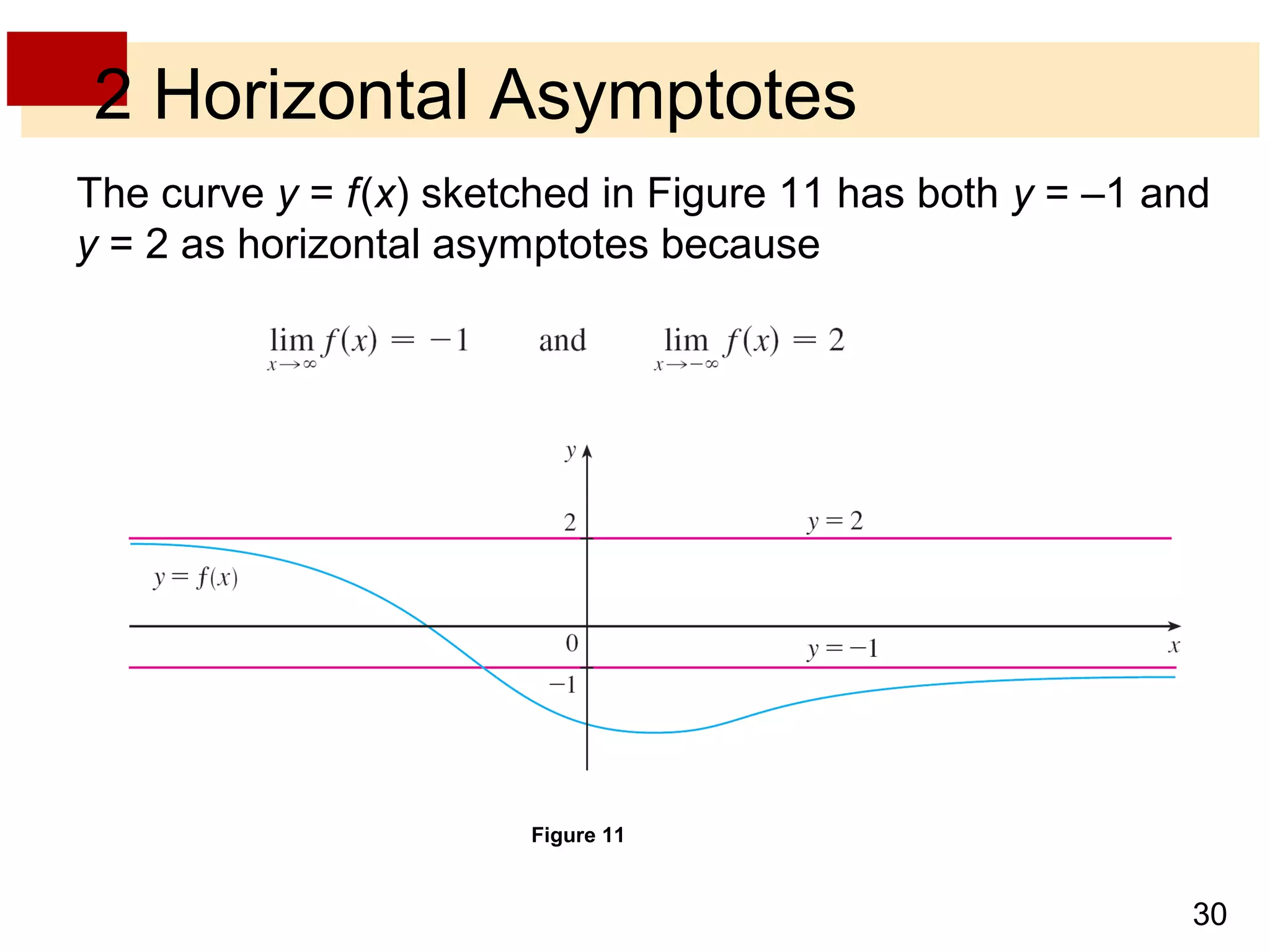
- Horizontal asymptotes occur when a function approaches a particular line y = L as x increases or decreases without bound.
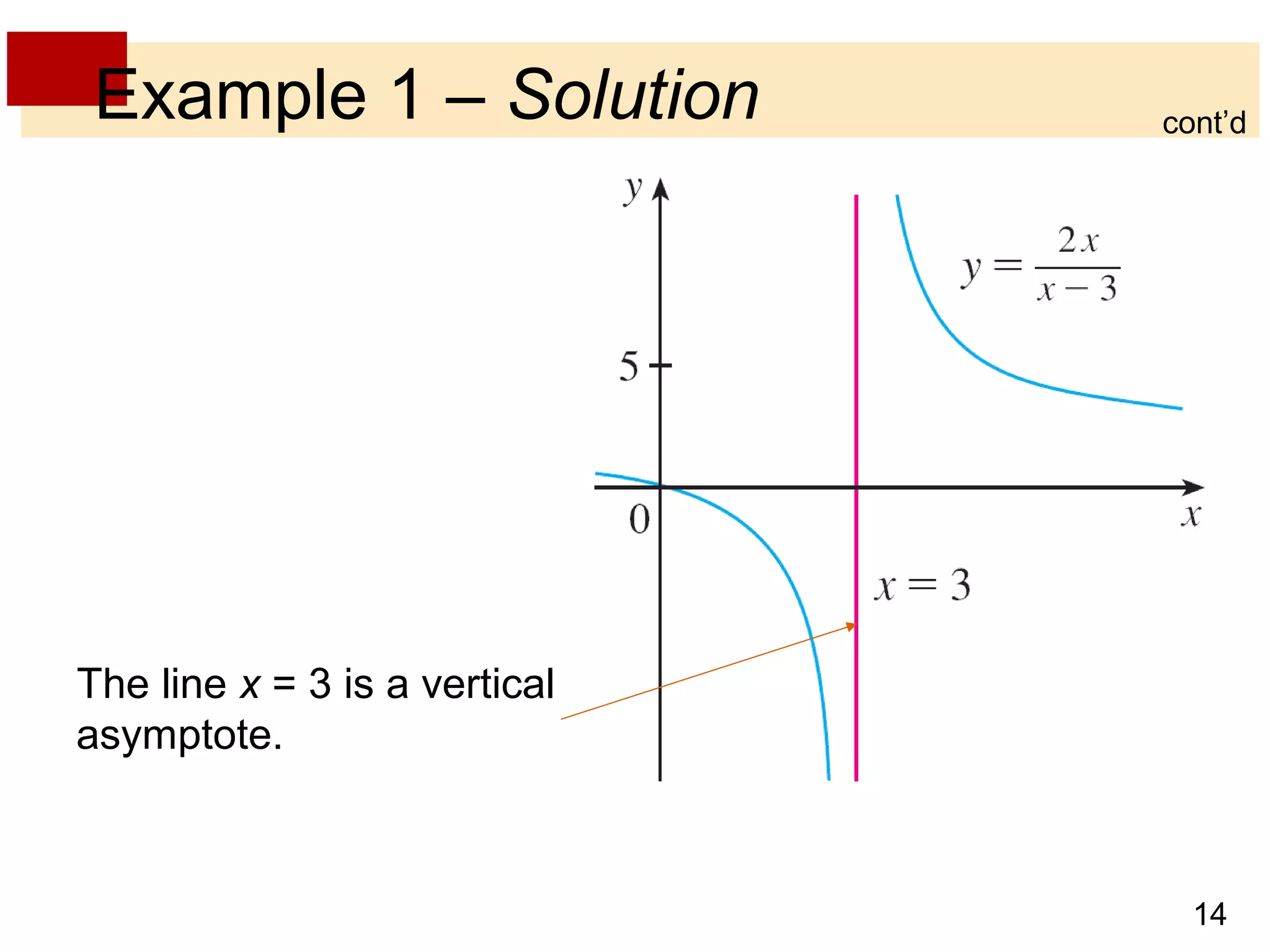
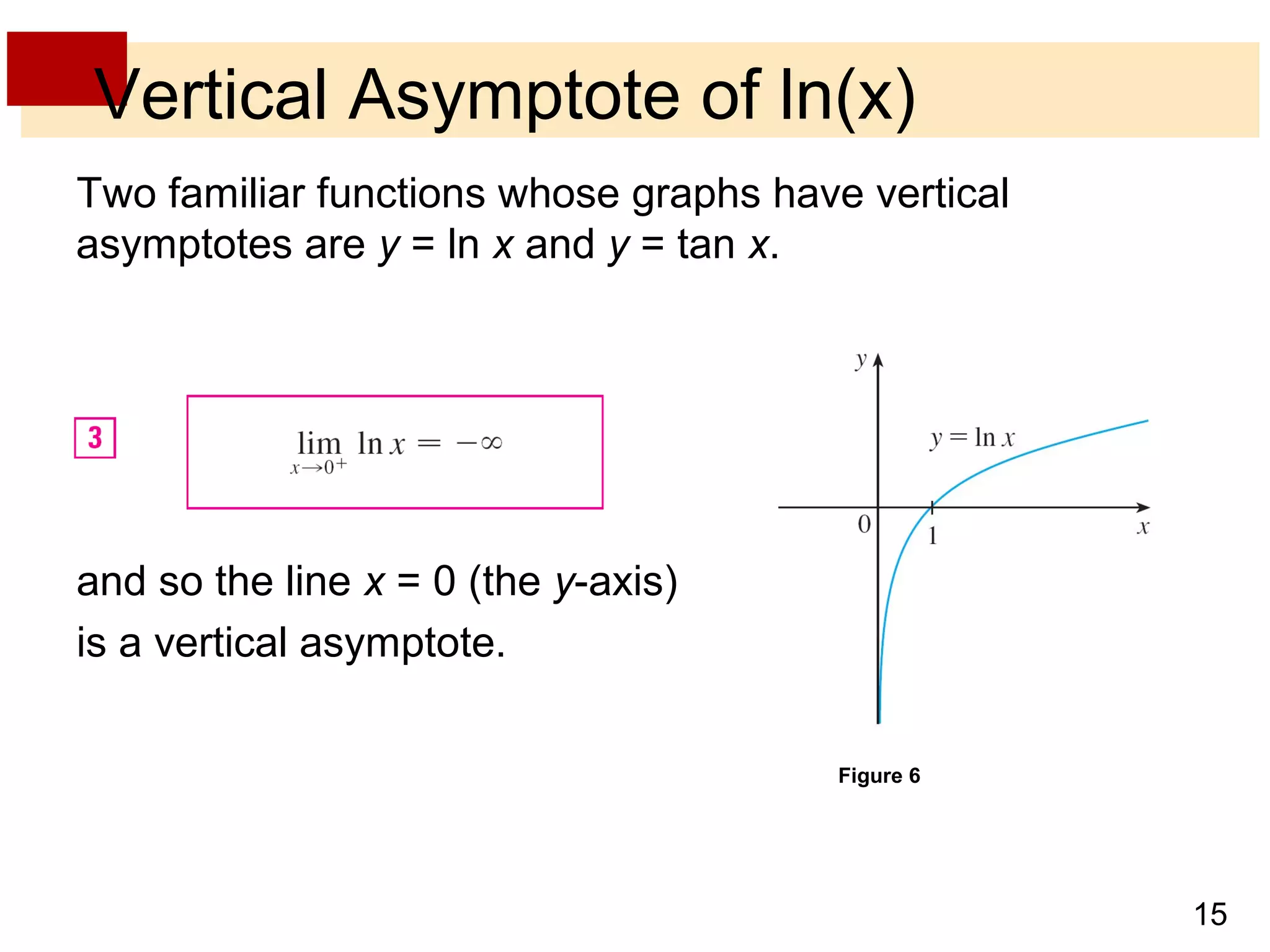
- Vertical asymptotes occur when a function's value increases or decreases without