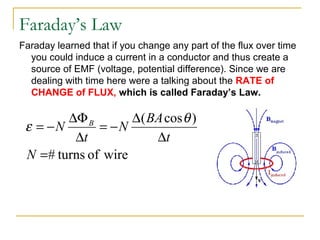
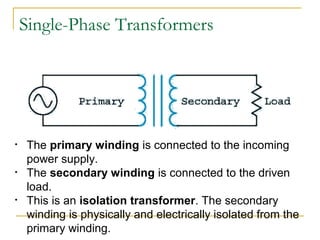
Electromagnetic induction occurs when a changing magnetic field induces a current in a conductor. Magnetic flux is the measure of the magnetic field passing through an area. Faraday's law states that an electromotive force (EMF) is induced in a conductor when there is a change in magnetic flux over time. Transformers use this principle to change voltage levels using a primary and secondary coil wound around an iron core. Lenz's law describes how the induced current will flow in a direction that creates an opposing magnetic field to the changing field that created it.

1. ElectroMagnetic Induction

2. Magnetic Induction
As the magnet moves back and forth a current is said
to be INDUCED in the wire.

3. Magnetic Flux
The first step to understanding the complex nature of
electromagnetic induction is to understand the idea
of magnetic flux.
Flux is a general term associated with a FIELD that is bound by a
certain AREA. So MAGNETIC FLUX is any AREA that has a
MAGNETIC FIELD passing through it.
A
B

4. Faraday’s Law
Faraday learned that if you change any part of the flux over time
you could induce a current in a conductor and thus create a
source of EMF (voltage, potential difference). Since we are
dealing with time here were a talking about the RATE of
CHANGE of FLUX, which is called Faraday’s Law.
wireofturns#
)cos(
=
∆
∆
−=
∆
∆Φ
−=
N
t
BA
N
t
N B θ
ε

5. Useful Applications
AC Generators use Faraday’s
law to produce rotation and
thus convert electrical and
magnetic energy into
rotational kinetic energy.
This idea can be used to
run all kinds of motors.
Since the current in the coil
is AC, it is turning on and
off thus creating a
CHANGING magnetic field
of its own. Its own
magnetic field interferes
with the shown magnetic
field to produce rotation.

6. Lenz’s Law
Lenz's law gives the direction of the induced emf and current
resulting from electromagnetic induction. In effect, electro
magnetically induced emf and hence the current flows in a coil or
a circuit in such a direction that the magnetic field setup by it
always opposes the cause which produces it.
t
N B
∆
∆Φ
−=εLenz’s Law

7. Inductance
 The ratio of magnetic flux to current is the
inductance.
 Inductance is measured in henry.
 1 H = 1 T m2
/ A
 More common, 1 H = 1 V / A / s
 The inductance can be derived for an ideal
solenoid.
I
L
Φ
=
l
rN
l
AN
L
22
0
2
0 πµµ
==

8. Induced EMF
 Faraday’s law gives the
magnitude of the induced
emf.
 Depends on rate of change
 The definition of inductance
gives a relationship between
voltage and current.
 More useful in circuits
 Inductive elements in a
circuit act like batteries.
 Stabilizes current
t
M
∆
∆Φ
−=ε
t
I
L
∆
∆
−=ε

9. Self Inductance
The property of the coil due to which it opposes the change of current flowing
through it is called self inductance
Suppose that we have a coil having N turns carrying a current I
That means that there is a magnetic flux through the coil
This flux can also be written as being proportional to the current
ILN B =Φ
with L being the self inductance having the same units as the mutual inductance

10. If the current changes, then the magnetic flux through the coil will also change,
giving rise to an induced emf in the coil
This induced emf will be such as to oppose the change in the current with its
value given by
dt
dI
L−=ε
If the current I is increasing, then
If the current I is decreasing, then
Self Inductance

11. There are circuit elements that behave in this manner and they are called
inductors and they are used to oppose any change in the current in the circuit
As to how they actually affect a circuit’s behavior will be discussed shortly
Self Inductance

12. Mutual Inductance
 The property of the coil due to
which it opposes the change of
current in neighboring coil is
called mutual inductance.
 The definition of inductance
applies to transformers.
 Mutual inductance vs self-
inductance
 Mutual inductance applies to
both windings.
AV∆
AN BN
R
t
NV M
BB
∆
∆Φ
−=∆ t
I
M
t
N M
B
∆
∆
=
∆
∆Φ
−=ε

13. Transformers
 A transformer is a device that changes ac electric power at
one voltage level to ac electric power at another voltage
level through the action of a magnetic field.
 There are two or more stationary electric circuits that are
coupled magnetically.
 It involves interchange of electric energy between two or
more electric systems
 Transformers provide much needed capability of changing
the voltage and current levels easily.
 They are used to step-up generator voltage to an appropriate
voltage level for power transfer.
 Stepping down the transmission voltage at various levels for
distribution and power utilization.

14. Transformers
Probably one of the greatest inventions of all time is the
transformer. AC Current from the primary coil moves quickly
BACK and FORTH (thus the idea of changing!) across the
secondary coil. The moving magnetic field caused by the
changing field (flux) induces a current in the secondary coil.
If the secondary coil has MORE turns
than the primary you can step up the
voltage and runs devices that would
normally need MORE voltage than
what you have coming in. We call this
a STEP UP transformer.
We can use this idea in reverse as well
to create a STEP DOWN transformer.

15. Single-Phase Transformers
• A transformer is a magnetically operated
machine.
• All values of a transformer are proportional
to its turns ratio.

16. Single-Phase Transformers
• The primary winding is connected to the incoming
power supply.
• The secondary winding is connected to the driven
load.
• This is an isolation transformer. The secondary
winding is physically and electrically isolated from the
primary winding.

17. Working of a transformer
1. When current in the primary coil
changes being alternating in
nature, a changing magnetic field
is produced
2. This changing magnetic field gets
associated with the secondary
through the soft iron core
3. Hence magnetic flux linked with
the secondary coil changes.
4. Which induces e.m.f. in the
secondary.

18. Single-Phase Transformers
• The isolation transformer greatly
reduces voltage spikes.

19. Single-Phase Transformers
• Each set of windings (primary and secondary) is formed from loops of wire
wrapped around the core.
• Each loop of wire is called a turn.
• The ratio of the primary and secondary voltages is determined by the ratio of
the number of turns in the primary and secondary windings.
• The volts-per-turn ratio is the same on both the primary and secondary
windings.

20. Constructional detail : Shell type
• Windings are wrapped around the center leg of a
laminated core.

21. Core type
• Windings are wrapped around two sides of a laminated square
core.

22. The Equivalent Circuit of a Transformer
The losses that occur in transformers have to be accounted for in any
accurate model of transformer behavior.
1. Copper (I2
R) losses. Copper losses are the resistive heating losses in the
primary and secondary windings of the transformer. They are proportional
to the square of the current in the windings.
2. Eddy current losses. Eddy current losses are resistive heating losses in
the core of the transformer. They are proportional to the square of the
voltage applied to the transformer.
3. Hysteresis losses. Hysteresis losses are associated with the
rearrangement of the magnetic domains in the core during each half-cycle.
They are a complex, nonlinear function of the voltage applied to the
transformer.
4. Leakage flux. The fluxes which escape the core and pass through only
one of the transformer windings are leakage fluxes. These escaped fluxes
produce a self-inductance in the primary and secondary coils, and the
effects of this inductance must be accounted for.

23. voltageload-no
voltageload-fullvoltageload-no
regulationVoltage
−
=






=
1
2
12
N
N
VV
p
s
p
s
N
N
V
V
=
Secondary voltage on no-load
V2 is a secondary terminal voltage on full load






−





=
1
2
1
2
1
2
1
regulationVoltage
N
N
V
V
N
N
V
Substitute we have

24. ECE 441 24
Voltage Regulation
% 100%
nl rated
rated
E V
reg per unit regulation
V
regulation per unit
−
= = − −
= − ×
Enl = no-load output voltage
Vrated = voltmeter reading at the output
terminals when the transformer is
supplying the rated apparent power

25. 25
When the breaker is open, no current flows in Req,LS ,
jXeq,LS , or ZLOAD,LS , therefore
Vout = VLS = E’LS = Enl

26. 26
With rated load on the secondary, E’LS = ILSZeq,LS + VLS
ILS = rated low-side current at a specified power factor
VLS = rated low-side voltage
Zeq,LS = equivalent impedance of the transformer
referred to the low-side
E’LS = no-load low-side voltage

27. Transformer Efficiency
Transformer efficiency is defined as (applies to motors, generators and
transformers):
%100×=
in
out
P
P
η
%100×
+
=
lossout
out
PP
P
η
Types of losses incurred in a transformer:
Copper I2
R losses
Hysteresis losses
Eddy current losses
Therefore, for a transformer, efficiency may be calculated using the following:
%100
cos
cos
x
IVPP
IV
SScoreCu
SS
θ
θ
η
++
=