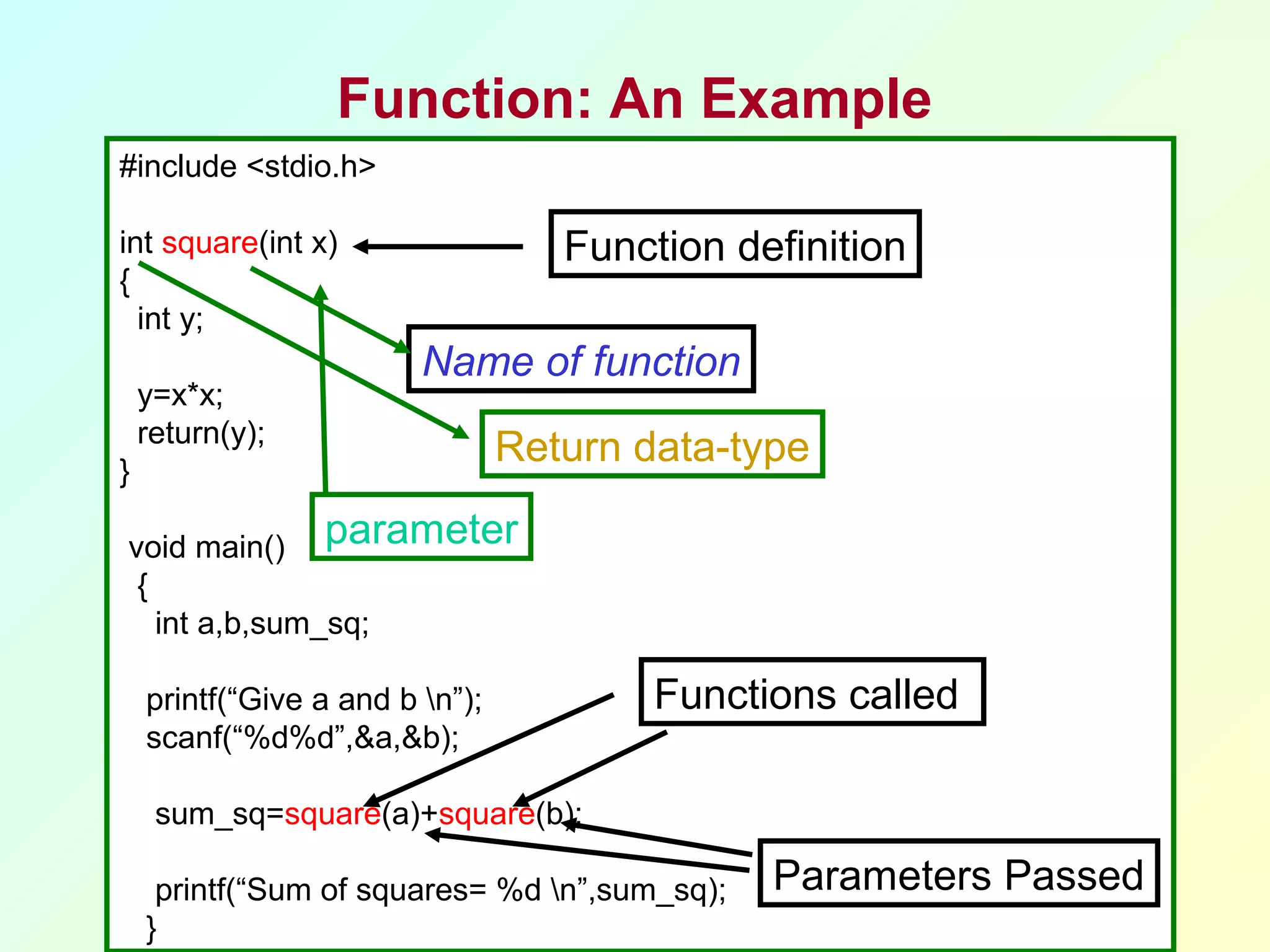
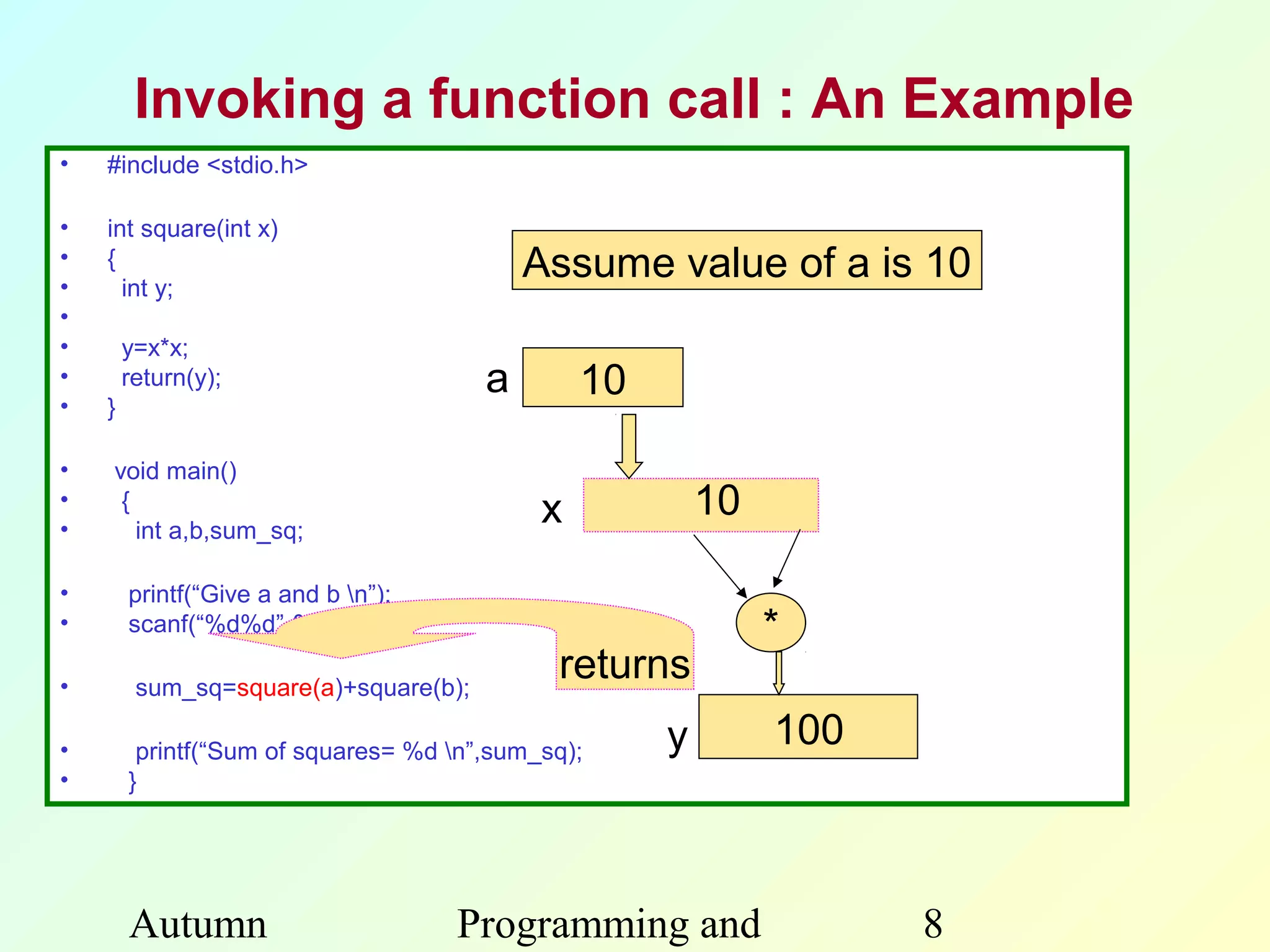
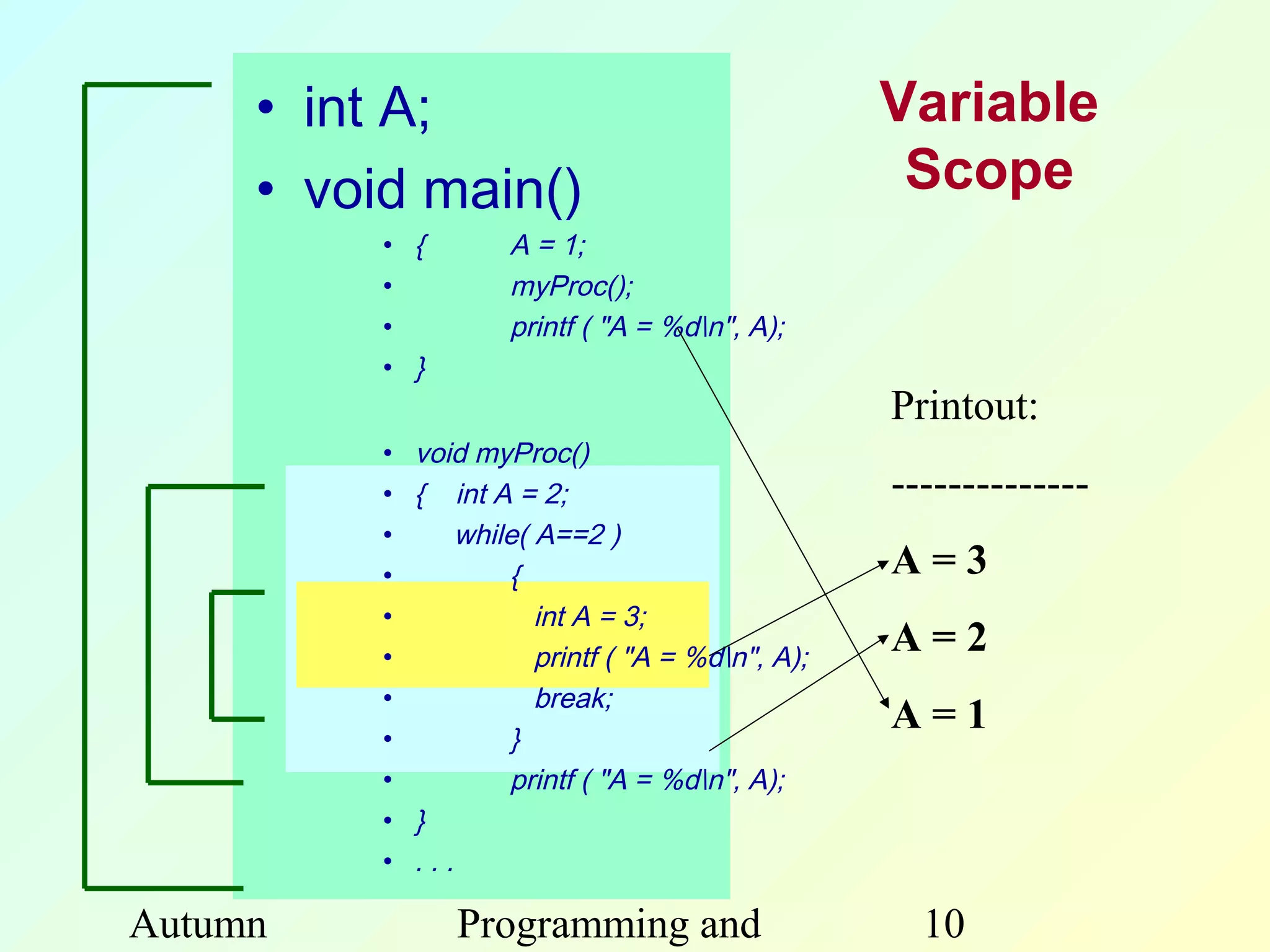
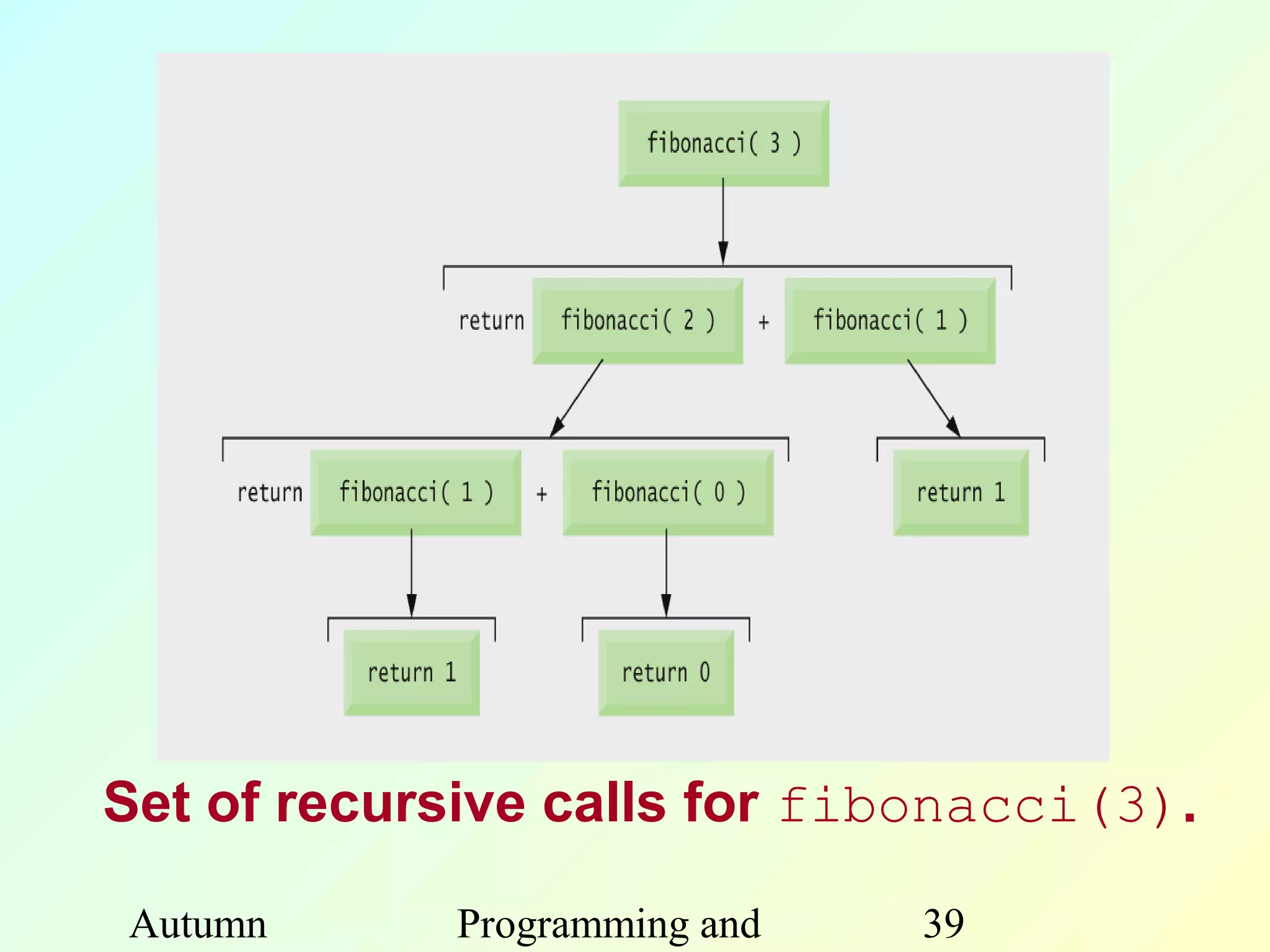
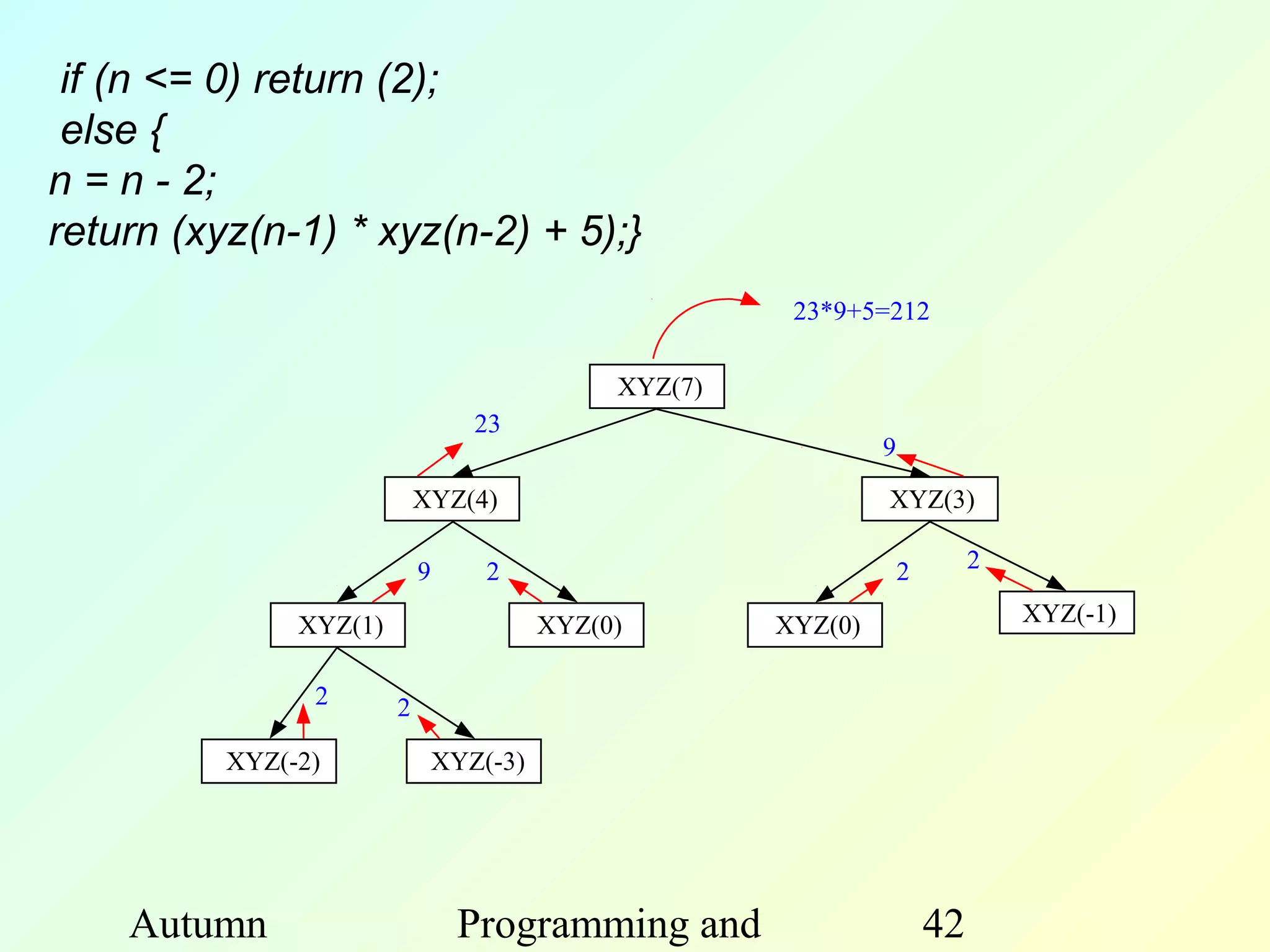
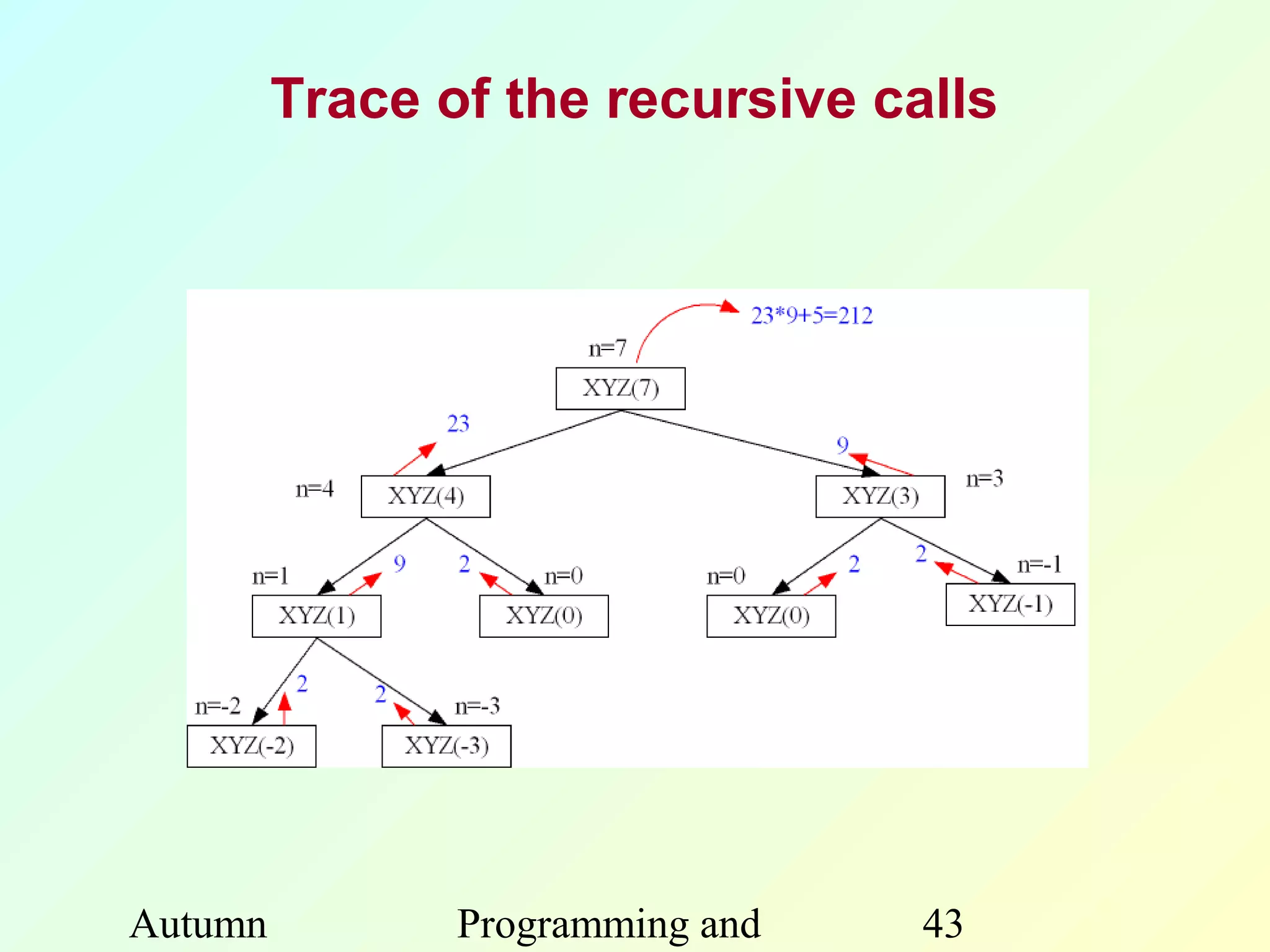
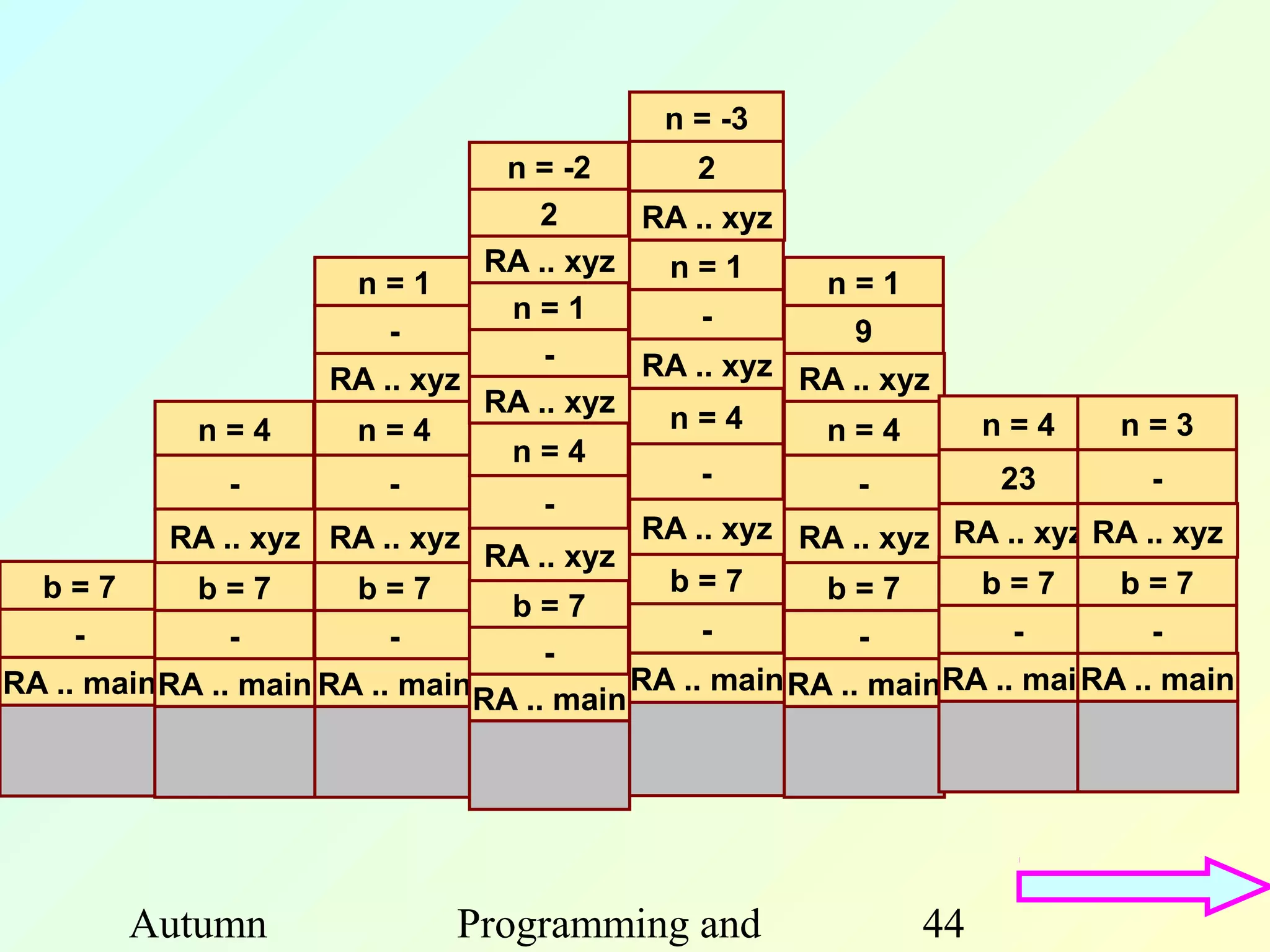
The document discusses functions in C programming. It begins by explaining what functions are and why they are useful. Functions help modularize programs, avoid code repetition, and allow for software reusability. Key benefits of using functions include divide and conquer programming and abstraction. The document then provides examples of function definitions, prototypes, parameters, return values, and scope. It also discusses calling functions, libraries, recursion, and other concepts related to functions in C.

1. Functions
Courtsey: University of Pittsburgh-CSD-Khalifa
Autumn Programming and 1

2. Class Test I: Time and Venue
• Date: August 20, 2009
• Time: 6:00 PM to 7:00 PM
– Students must occupy seat within 5:45 PM, and carry
library card with them.
• Venue: VIKRAMSHILA COMPLEX / MAIN BUILDING
- Section 7 & 10 (AE-EC) :: AE, AG, AR, BT, CE, CH, CS , CY, EC Room V1
– Section 8 & 10 (Rest) :: Room V2
– Section 9 (AE-CS):: AE, AG, AR, BT, CE, CH, CS Room V3
– Section 9 (Rest):: Room V4
– Section 11:: F 116
– Section 12:: F 142
Autumn Programming and 2

3. Functions: Why?
• Functions
– Modularize a program
– All variables declared inside functions are local
variables
• Known only in function defined
– Parameters
• Communicate information between functions
• Local variables
• Benefits
– Divide and conquer
• Manageable program development
– Software reusability
• Use existing functions as building blocks for new
programs
• Abstraction - hide internal details (library functions)
– Avoids code repetition
Autumn Programming and 3

4. Functions: Why?
• Divide and conquer
– Construct a program from smaller
pieces or components
– Each piece more manageable than the
original program
Autumn Programming and 4

5. Program Modules in C
• Functions
– Modules in C
– Programs written by combining user-
defined functions with library functions
• C standard library has a wide variety of
functions
• Makes programmer's job easier - avoid
reinventing the wheel
Autumn Programming and 5

6. Program Modules in C
• Function calls
– Invoking functions
• Provide function name and arguments
(data)
• Function performs operations or
manipulations
• Function returns results
– Boss asks worker to complete task
• Worker gets information, does task, returns
result
• Information hiding: boss does not know
details
Autumn Programming and 6

7. Function: An Example
#include <stdio.h>
int square(int x) Function definition
{
int y;
Name of function
y=x*x;
return(y);
}
Return data-type
void main() parameter
{
int a,b,sum_sq;
printf(“Give a and b n”); Functions called
scanf(“%d%d”,&a,&b);
sum_sq=square(a)+square(b);
printf(“Sum of squares= %d n”,sum_sq); Parameters Passed
Autumn
} Programming and 7

8. Invoking a function call : An Example
• #include <stdio.h>
• int square(int x)
•
•
{
int y;
Assume value of a is 10
•
• y=x*x;
• return(y); a 10
• }
• void main()
• {
x 10
• int a,b,sum_sq;
• printf(“Give a and b n”);
• scanf(“%d%d”,&a,&b); *
• sum_sq=square(a)+square(b);
returns
• printf(“Sum of squares= %d n”,sum_sq); y 100
• }
Autumn Programming and 8

9. Function Definitions
• Function definition format (continued)
return-value-type function-name( parameter-list )
{
declarations and statements
}
– Declarations and statements: function body (block)
• Variables can be declared inside blocks (can be
nested)
• Function can not be defined inside another function
– Returning control
• If nothing returned
– return;
– or, until reaches right brace
• If something returned
– return expression;
Autumn Programming and 9

10. • int A; Variable
• void main() Scope
• { A = 1;
• myProc();
• printf ( "A = %dn", A);
• }
Printout:
• void myProc()
• { int A = 2; --------------
• while( A==2 )
• { A=3
• int A = 3;
• printf ( "A = %dn", A);
A=2
• break;
• }
A=1
• printf ( "A = %dn", A);
• }
• ...
Autumn Programming and 10

11. Math Library Functions
• Math library functions
– perform common mathematical calculations
– #include <math.h>
• Format for calling functions
FunctionName (argument);
• If multiple arguments, use comma-separated list
– printf( "%5.2f", sqrt( 900.0 ) );
• Calls function sqrt, which returns the square root of its
argument
• All math functions return data type double
– Arguments may be constants, variables, or expressions
Autumn Programming and 11

12. Math Library Functions
• double acos(double x) -- Compute arc cosine of x.
double asin(double x) -- Compute arc sine of x.
double atan(double x) -- Compute arc tangent of x.
double atan2(double y, double x) -- Compute arc tangent of y/x.
double ceil(double x) -- Get smallest integral value that exceeds x.
double cos(double x) -- Compute cosine of angle in radians.
double cosh(double x) -- Compute the hyperbolic cosine of x.
div_t div(int number, int denom) -- Divide one integer by another.
double exp(double x -- Compute exponential of x
double fabs (double x ) -- Compute absolute value of x.
double floor(double x) -- Get largest integral value less than x.
double fmod(double x, double y) -- Divide x by y with integral quotient and return
remainder.
double frexp(double x, int *expptr) -- Breaks down x into mantissa and exponent of no.
labs(long n) -- Find absolute value of long integer n.
double ldexp(double x, int exp) -- Reconstructs x out of mantissa and exponent of two.
ldiv_t ldiv(long number, long denom) -- Divide one long integer by another.
double log(double x) -- Compute log(x).
double log10 (double x ) -- Compute log to the base 10 of x.
double modf(double x, double *intptr) -- Breaks x into fractional and integer parts.
double pow (double x, double y) -- Compute x raised to the power y.
double sin(double x) -- Compute sine of angle in radians.
double sinh(double x) - Compute the hyperbolic sine of x.
double sqrt(double x) -- Compute the square root of x.
void srand(unsigned seed) -- Set a new seed for the random number generator (rand).
double tan(double x) -- Compute tangent of angle in radians.
double tanh(double x) -- Compute the hyperbolic tangent of x.
Autumn Programming and 12

13. Function Prototypes
• Function prototype
– Function name
– Parameters - what the function takes in
– Return type - data type function returns (default int)
– Used to validate functions
– Prototype only needed if function definition comes after
use in program
int maximum( int, int, int );
• Takes in 3 ints
• Returns an int
• Promotion rules and conversions
– Converting to lower types can lead to errors
Autumn Programming and 13

14. Header Files
• Header files
– contain function prototypes for library functions
– <stdlib.h> , <math.h> , etc
– Load with #include <filename>
#include <math.h>
• Custom header files
– Create file with functions
– Save as filename.h
– Load in other files with #include "filename.h"
– Reuse functions
Autumn Programming and 14

15. /* Finding the maximum of three integers */
#include <stdio.h>
int maximum( int, int, int ); /* function prototype */
int main()
{
int a, b, c;
printf( "Enter three integers: " );
scanf( "%d%d%d", &a, &b, &c );
printf( "Maximum is: %dn", maximum( a, b, c ) );
return 0;
}
/* Function maximum definition */
int maximum( int x, int y, int z )
{
int max = x;
if ( y > max )
max = y;
if ( z > max )
max = z;
return max;
}
Autumn Programming and 15

16. Calling Functions: Call by Value and Call by
Reference
• Used when invoking functions
• Call by value
– Copy of argument passed to function
– Changes in function do not affect original
– Use when function does not need to modify argument
• Avoids accidental changes
• Call by reference
– Passes original argument
– Changes in function affect original
– Only used with trusted functions
• For now, we focus on call by value
Autumn Programming and 16

17. An Example: Random Number Generation
• rand function
– Prototype defined in <stdlib.h>
– Returns "random" number between 0 and RAND_MAX (at
least 32767)
i = rand();
– Pseudorandom
• Preset sequence of "random" numbers
• Same sequence for every function call
• Scaling
– To get a random number between 1 and n
1 + ( rand() % n )
• rand % n returns a number between 0 and n-1
• Add 1 to make random number between 1 and n
1 + ( rand() % 6) // number between 1 and 6
Autumn Programming and 17

18. Random Number Generation: Contd.
• srand function
– Prototype defined in <stdlib.h>
– Takes an integer seed - jumps to location in
"random" sequence
srand( seed );
Autumn Programming and 18

19. 1 /* A programming example
2 Randomizing die-rolling program */
3 #include <stdlib.h>
4 #include <stdio.h>
5 Algorithm
6 int main()
1. Initialize seed
7 {
8 int i;
2. Input value for seed
9 unsigned seed; 2.1 Use srand to change random sequence
10 2.2 Define Loop
11 printf( "Enter seed: " );
3. Generate and output random numbers
12 scanf( "%u", &seed );
13 srand( seed );
14
15 for ( i = 1; i <= 10; i++ ) {
16 printf( "%10d ", 1 + ( rand() % 6 ) );
17
18 if ( i % 5 == 0 )
19 printf( "n" );
20 }
21
22 return 0;
23 } Autumn Programming and 19

20. Program Output
Enter seed: 67
6 1 4 6 2
1 6 1 6 4
Enter seed: 867
2 4 6 1 6
1 1 3 6 2
Enter seed: 67
6 1 4 6 2
1 6 1 6 4
Autumn Programming and 20

21. Another Example: A Game of Chance
• Rules
– Roll two dice
• 7 or 11 on first throw, player wins
• 2, 3, or 12 on first throw, player loses
• 4, 5, 6, 8, 9, 10 - value becomes player's "point"
– Player must roll his point before rolling 7 to
win
Autumn Programming and 21

22. Programme Structure
• 1. rollDice prototype
•
1.1 Initialize variables
•
1.2 Seed srand
• 2. Define switch statement for win/loss/continue
• 2.1 Loop
Autumn Programming and 22

23. 1 /* A Game of Chance
2 Rolling Two Dice*/
3 #include <stdio.h>
4 #include <stdlib.h>
5 #include <time.h>
6
7 int rollDice( void );
8
9 int main()
10 {
11 int gameStatus, sum, myPoint;
12
13 srand( time( NULL ) ); /* Randomizing seed by time(NULL) */
14 sum = rollDice(); /* first roll of the dice */
15
16 switch ( sum ) {
17 case 7: case 11: /* win on first roll */
18 gameStatus = 1;
19 break;
20 case 2: case 3: case 12: /* lose on first roll */
21 gameStatus = 2;
22 break;
23 default: /* remember point */
24 gameStatus = 0;
25 myPoint = sum;
26 printf( "Point is %dn", myPoint );
27 break;
28 }
29
30 while ( gameStatus == 0 ) { /* keep rolling */
sum = rollDice();
31
32
Autumn Programming and 23

24. 33 if ( sum == myPoint ) /* win by making point */
34 gameStatus = 1;
35 else
36 if ( sum == 7 ) /* lose by rolling 7 */
37 gameStatus = 2;
38 }
39
40 if ( gameStatus == 1 )
41 printf( "Player winsn" );
42 else
43 printf( "Player losesn" );
44
45 return 0;
46 }
47
48 int rollDice( void )
49 {
50 int die1, die2, workSum;
51
52 die1 = 1 + ( rand() % 6 );
53 die2 = 1 + ( rand() % 6 );
54 workSum = die1 + die2;
55
56
2.2 Print win/loss
printf( "Player rolled %d + %d = %dn", die1, die2, workSum );
return workSum;
57 }
Autumn Programming and 24

25. Program Output
Player rolled 6 + 5 = 11
Player wins
Player rolled 6 + 6 = 12
Player loses
Player rolled 4 + 6 = 10
Point is 10
Player rolled 2 + 4 = 6
Player rolled 6 + 5 = 11
Player rolled 3 + 3 = 6
Player rolled 6 + 4 = 10
Player wins
Player rolled 1 + 3 = 4
Point is 4
Player rolled 1 + 4 = 5
Player rolled 5 + 4 = 9
Player rolled 4 + 6 = 10
Player rolled 6 + 3 = 9
Player rolled 1 + 2 = 3
Player rolled 5 + 2 = 7
Player loses
Autumn Programming and 25

26. Recursion
• A process by which a function calls itself
repeatedly.
– Either directly.
• X calls X.
– Or cyclically in a chain.
• X calls Y, and Y calls X.
• Used for repetitive computations in which
each action is stated in terms of a
previous result.
– fact(n) = n * fact (n-1)
Autumn Programming and 26

27. Contd.
• For a problem to be written in recursive
form, two conditions are to be satisfied:
– It should be possible to express the problem in
recursive form.
– The problem statement must include a
stopping condition
fact(n) = 1, if n = 0
= n * fact(n-1), if n > 0
Autumn Programming and 27

28. Example 1 :: Factorial
long int fact (n)
int n;
{
if (n = = 0)
return (1);
else
return (n * fact(n-1));
}
Autumn Programming and 28

29. Mechanism of Execution
• When a recursive program is executed,
the recursive function calls are not
executed immediately.
– They are kept aside (on a stack) until the
stopping condition is encountered.
– The function calls are then executed in reverse
order.
Autumn Programming and 29

30. Example :: Calculating fact(4)
– First, the function calls will be processed:
fact(4) = 4 * fact(3)
fact(3) = 3 * fact(2)
fact(2) = 2 * fact(1)
fact(1) = 1 * fact(0)
– The actual values return in the reverse order:
fact(0) = 1
fact(1) = 1 * 1 = 1
fact(2) = 2 * 1 = 2
fact(3) = 3 * 2 = 6
fact(4) = 4 * 6 = 24
Autumn Programming and 30

31. Factorials: Contd.
• Example: factorials
– 5! = 5 * 4 * 3 * 2 * 1
– Notice that
• 5! = 5 * 4!
• 4! = 4 * 3! ...
– Can compute factorials recursively
– Solve base case (1! = 0! = 1) then plug in
• 2! = 2 * 1! = 2 * 1 = 2;
• 3! = 3 * 2! = 3 * 2 = 6;
Autumn Programming and 31

32. Recursive evaluation of 5!.
Autumn Programming and 32

33. 1 /* An example */ 22 /* recursive definition of function factorial */
2 /* Recursive factorial function */ 23 long factorial( long number )
3 #include <stdio.h> 24 {
4 25 /* base case */
5 long factorial( long number ); /* function prototype */ 26 if ( number <= 1 ) {
6 27 return 1; Terminating
7 /* function main begins program execution */ 28 } /* end if */ Criterion
8 int main( void ) 29 else { /* recursive step */
9 { 30 return ( number * factorial( number - 1 ) );
10 int i; /* counter */ 31 } /* end else */
11 32
12 /* loop 11 times; during each iteration, calculate 33 } /* end function factorial */
13 factorial( i ) and display result */
14 for ( i = 0; i <= 10; i++ ) { 0! = 1
1! = 1
15 printf( "%2d! = %ldn", i, factorial( i ) ); 2! = 2
16 } /* end for */ 3! = 6
17 4! = 24
18 return 0; /* indicates successful termination */ 5! = 120
6! = 720
19 7! = 5040
20 } /* end main */ 8! = 40320
21 9! = 362880
10! = 3628800
Autumn Programming and 33

34. Another Example :: Fibonacci number
• Fibonacci number f(n) can be defined as:
f(0) = 0
f(1) = 1
f(n) = f(n-1) + f(n-2), if n > 1
– The successive Fibonacci numbers are:
0, 1, 1, 2, 3, 5, 8, 13, 21, …..
• Function definition:
int f (int n)
{
if (n < 2) return (n);
else return (f(n-1) + f(n-2));
}
Autumn Programming and 34

35. Tracing Execution
• How many times the f(4)
function is called
when evaluating f(4) ? f(3) f(2)
f(2) f(1) f(1) f(0)
• Inefficiency: f(1) f(0)
– Same thing is
computed several 9 times
times.
Autumn Programming and 35

36. Example Codes: fibonacci()
– Code for the fibonacci function
long fibonacci( long n )
{
if (n == 0 || n == 1) // base case
return n;
else
return fibonacci( n - 1) +
fibonacci( n – 2 );
}
Autumn Programming and 36

37. 1 /* Another Example:
2 Recursive fibonacci function */ 27 /* Recursive definition of function fibonacci *
3 #include <stdio.h>
4 28 long fibonacci( long n )
5 long fibonacci( long n ); /* function prototype */ 29 {
6
30 /* base case */
7 /* function main begins program execution */
8 int main( void ) 31 if ( n == 0 || n == 1 ) {
9 { 32 return n;
10 long result; /* fibonacci value */
33 } /* end if */
11 long number; /* number input by user */
12 34 else { /* recursive step */
13 /* obtain integer from user */ 35 return fibonacci( n - 1 ) + fibonacci( n - 2 );
14 printf( "Enter an integer: " );
36 } /* end else */
15 scanf( "%ld", &number );
16 37
17 /* calculate fibonacci value for number input by user */ 38 } /* end function fibonacci */
18 result = fibonacci( number );
19
20 /* display result */
21 printf( "Fibonacci( %ld ) = %ldn", number, result );
22 Enter an integer: 0
Fibonacci( 0 ) = 0
23 return 0; /* indicates successful termination */
24
25 } /* end main */
26
Enter an integer: 1
Fibonacci( 1 ) = 1
Autumn ProgrammingEnter an integer:12 37
and
Fibonacci( 2 ) =

38. (continued from previous slide…)
Enter an integer: 3
Fibonacci( 3 ) = 2
Enter an integer: 4
Fibonacci( 4 ) = 3
Enter an integer: 5
Fibonacci( 5 ) = 5
Enter an integer: 6
Fibonacci( 6 ) = 8
)
Autumn Programming and 38

39. Set of recursive calls for fibonacci(3).
Autumn Programming and 39

40. Performance Tip
• Avoid Fibonacci-style recursive
programs which result in an
exponential “explosion” of calls.
Autumn Programming and 40

41. Recursion and activation records:
an example
#include <stdio.h> int xyz (int n)
main() {
{ if (n <= 0) return (2);
int a, b; else
b = 7; {
a = xyz (b); n = n - 2;
printf ("a=%d, b=%d n", a, b); return (xyz(n-1) * xyz(n-2) + 5);
} }
}
What is the output?
How many times xyz()
Called?
Autumn Programming and 41

42. if (n <= 0) return (2);
else {
n = n - 2;
return (xyz(n-1) * xyz(n-2) + 5);}
23*9+5=212
XYZ(7)
23
9
XYZ(4) XYZ(3)
9 2 2 2
XYZ(1) XYZ(0) XYZ(0) XYZ(-1)
2 2
XYZ(-2) XYZ(-3)
Autumn Programming and 42

43. Trace of the recursive calls
Autumn Programming and 43

44. n = -3
n = -2 2
2 RA .. xyz
RA .. xyz n=1
n=1 n=1
n=1 -
- 9
- RA .. xyz RA .. xyz
RA .. xyz
RA .. xyz
n=4 n=4 n=4 n=4 n=4 n=3
n=4
- - - - 23 -
-
RA .. xyz RA .. xyz RA .. xyz RA .. xyz RA .. xyz RA .. xyz
RA .. xyz
b=7 b=7 b=7 b=7 b=7 b=7 b=7
b=7
- - - - - - -
-
RA .. mainRA .. main RA .. main RA .. main RA .. mainRA .. main .. main
RA
RA .. main
Autumn Programming and 44

45. What is the value of a and b?
How many times the recursive function called?
(i) a=212, b=7
(i) xyz( ) called 9 times
Autumn Programming and 45

46. Recursion vs. Iteration
• Repetition
– Iteration: explicit loop
– Recursion: repeated function calls
• Termination
– Iteration: loop condition fails
– Recursion: base case recognized
• Both can have infinite loops
• Balance
– Choice between performance (iteration) and
good software engineering (recursion)
Autumn Programming and 46

47. Performance Tip
• Avoid using recursion in
performance situations. Recursive
calls take time and consume
additional memory.
Autumn Programming and 48