12 derivatives and integrals of inverse trigonometric functions x

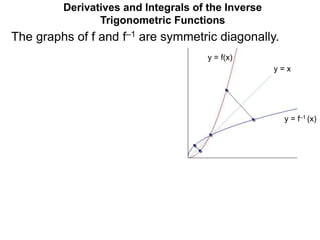
y = f(x)
y = f–1 (x)
The graphs of f and f–1 are symmetric diagonally.
y = x
Derivatives and Integrals of the Inverse
Trigonometric Functions

y = f(x)
y = f–1 (x)
y = x
(a, b)
Assume f(x) is differentiable
and (a, b) is a point on the
graph of y = f(x).

y = f(x)
y = f–1 (x)
y = x
(a, b)
graph of y = f(x). Hence the
slope at (a, b) is f ’(a).
slope = f ’(a)

y = f(x)
y = f–1 (x)
y = x
(a, b)
(b, a)
slope = f ’(a)
The reflection of (a, b) is (b, a)
on the graph of y = f–1(x).

y = f(x)
y = f–1 (x)
y = x
(a, b)
(b, a)
slope = f ’(a)
The slope of the tangent line at
(b, a) is (f–1)’(b).
slope = (f–1)’(b)

(b, a) is (f–1)’(b).
By the symmetry the tangents at (a, b) and at (b, a)
are the reflection of each other.
y = f(x)
y = f–1 (x)
y = x
(a, b)
(b, a)
slope = f ’(a)

(b, a) is (f–1)’(b).
are the reflection of each other. Diagonally-
symmetric lines have reciprocal slopes (why?)
y = f(x)
y = f–1 (x)
y = x
(a, b)
(b, a)
slope = f ’(a)

(b, a) is (f–1)’(b).
y = f(x)
y = f–1 (x)
y = x
(a, b)
(b, a)
slope = f ’(a)
Hence of (f–1)’(b) = 1
f ’(a)

(b, a) is (f–1)’(b).
y = f(x)
y = f–1 (x)
y = x
(a, b)
(b, a)
slope = f ’(a)
Hence of (f–1)’(b) = 1 = 1
f ’(f–1(b))f ’(a)

Suppose f and g are a pair of inverse functions,
then (f o g)(x) = x.

Differentiate both sides with respect to x and use
the chain rule:
[(f o g)(x)]' = x'

the chain rule:
[(f o g)(x)]' = x'
f '(g(x)) * g'(x) = 1

the chain rule:
[(f o g)(x)]' = x'
f '(g(x)) * g'(x) = 1
or
g'(x) = 1
f '(g(x))

the chain rule:
[(f o g)(x)]' = x'
f '(g(x)) * g'(x) = 1
or
g'(x) = 1
f '(g(x))
Set f = sin(x) and g = arcsin(x)

the chain rule:
[(f o g)(x)]' = x'
f '(g(x)) * g'(x) = 1
or
g'(x) = 1
f '(g(x))
Set f = sin(x) and g = arcsin(x) we obtain
[arcsin(x)]' = 1
dsin(y)
dy y=arcsin(x)

the chain rule:
[(f o g)(x)]' = x'
f '(g(x)) * g'(x) = 1
or
g'(x) = 1
f '(g(x))
Set f = sin(x) and g = arcsin(x) we obtain
[arcsin(x)]' = 1
dsin(y)
1
cos(arcsin(x))
=
dy y=arcsin(x)

[arcsin(x)]'
1
cos(arcsin(x))
=

θ=arcsin(x)
x
1
[arcsin(x)]'
1
cos(arcsin(x))
=

θ=arcsin(x)
x
1
1 – x2
[arcsin(x)]'
1
cos(arcsin(x))
=

θ=arcsin(x)
x
1
1 – x2
[arcsin(x)]'
1
cos(arcsin(x))
=
1
1 – x2
[arcsin(x)]' =

θ=arcsin(x)
x
1
1 – x2
[arcsin(x)]'
1
cos(arcsin(x))
=
1
1 – x2
[arcsin(x)]' =
–1 1
–π/2
π/2
x
y=arcsin(x)

θ=arcsin(x)
x
1
1 – x2
[arcsin(x)]'
1
cos(arcsin(x))
=
1
1 – x2
[arcsin(x)]' =
We use the same technique to obtain the
derivatives of the other inverse trig-functions.
–1 1
–π/2
π/2
x
y=arcsin(x)

θ=arcsin(x)
x
1
1 – x2
[arcsin(x)]'
1
cos(arcsin(x))
=
1
1 – x2
[arcsin(x)]' =
We use the same technique to obtain the
derivatives of the other inverse trig-functions.
–1 1
–π/2
π/2
x
y=arcsin(x)
We display the graphs of each inverse–trig and
list each of their derivatives below.

Derivatives of the Inverse Trig–Functions
1
1 – x2
[sin–1(x)] ' =
y =sin–1(x)

[cos–1(x)]' =
1
1 – x2
[sin–1(x)] ' =
–1
1 – x2
y =sin–1(x)
y =cos–1(x)

[cos–1(x)]' =
1
1 + x2
[tan–1(x)]' =
1
1 – x2
[sin–1(x)] ' =
–1
1 – x2
y =tan–1(x)
y =sin–1(x)
y =cos–1(x)

[cos–1(x)]' =
1
1 + x2
[tan–1(x)]' =
–1
1 + x2[cot–1(x)]' =
1
1 – x2
[sin–1(x)] ' =
–1
1 – x2
y =tan–1(x)
y =sin–1(x)
y =cos–1(x)
y =cot–1(x)

[cos–1(x)]' =
1
1 + x2
[tan–1(x)]' =
|x|x2 – 1
[sec–1(x)]' =
–1
1 + x2[cot–1(x)]' =
y =sec–1(x)
1
1 – x2
[sin–1(x)] ' =
–1
1 – x2
1
y =tan–1(x)
y =sin–1(x)
y =cos–1(x)
y =cot–1(x)

[cos–1(x)]' =
1
1 + x2
[tan–1(x)]' =
|x|x2 – 1
[sec–1(x)]' =
–1
1 + x2[cot–1(x)]' =
–1
|x|x2 – 1
[csc–1(x)]' =
y =sec–1(x) y =csc–1(x)
1
1 – x2
[sin–1(x)] ' =
–1
1 – x2
1
y =tan–1(x)
y =sin–1(x)
y =cos–1(x)
y =cot–1(x)

u'
1 – u2[sin–1(u)]' = –u'
1 – u2
[cos–1 (u)]' =
u'
1 + u2[tan–1(u)]' =
u'
|u|u2 – 1
[sec–1(u)]' =
–u'
1 + u2[cot–1(u)]' =
–u'
|u|u2 – 1
[csc–1(u)]' =
dsin-1(u)
dx
= 1
1 – u2
du
dx
–1
1 – u2
du
dx
1
1 + u2
du
dx
1
|u|u2 – 1
du
dx
dcos-1(u)
dx
=
dtan-1(u)
dx
=
dsec-1(u)
dx
=
–1
1 + u2
du
dx
dtan-1(u)
dx
=
–1
|u|u2 – 1
du
dx
dcsc-1(u)
dx
=
Below are the chain–rule versions where u = u(x).

–u'
1 – u2
[cos–1 (u)]' = u'
1 + u2[tan–1(u)]' =
u'
|u|u2 – 1
[sec–1(u)]' =
We’ll use the following formulas for the next example.

b. cos–1(ex )
Example A. Find the following derivatives.
a. tan–1(x3)
–u'
1 – u2
[cos–1 (u)]' = u'
1 + u2[tan–1(u)]' =
u'
|u|u2 – 1
[sec–1(u)]' =
2
c. sec–1(ln(x))

b. cos–1(ex )
2
Set u = x3,
a. tan–1(x3)
–u'
1 – u2
[cos–1 (u)]' = u'
1 + u2[tan–1(u)]' =
u'
|u|u2 – 1
[sec–1(u)]' =
c. sec–1(ln(x))

b. cos–1(ex )
2
Set u = x3, so [tan–1(x3)]' = (x3)'
1 + (x3)2
a. tan–1(x3)
–u'
1 – u2
[cos–1 (u)]' = u'
1 + u2[tan–1(u)]' =
u'
|u|u2 – 1
[sec–1(u)]' =
c. sec–1(ln(x))

b. cos–1(ex )
2
Set u = x3, so [tan–1(x3)]' = (x3)'
1 + (x3)2 = 3x2
1 + x6
a. tan–1(x3)
–u'
1 – u2
[cos–1 (u)]' = u'
1 + u2[tan–1(u)]' =
u'
|u|u2 – 1
[sec–1(u)]' =
c. sec–1(ln(x))

b. cos–1(ex )
Set u = ex,
2
Set u = x3, so [tan–1(x3)]' = (x3)'
1 + (x3)2 = 3x2
1 + x6
a. tan–1(x3)
–u'
1 – u2
[cos–1 (u)]' = u'
1 + u2[tan–1(u)]' =
u'
|u|u2 – 1
[sec–1(u)]' =
c. sec–1(ln(x))

b. cos–1(ex )
Set u = ex, so [cos-1(ex )]' =
2
2
1 – (ex )2
–(ex )'
2
2
Set u = x3, so [tan–1(x3)]' = (x3)'
1 + (x3)2 = 3x2
1 + x6
a. tan–1(x3)
–u'
1 – u2
[cos–1 (u)]' = u'
1 + u2[tan–1(u)]' =
u'
|u|u2 – 1
[sec–1(u)]' =
c. sec–1(ln(x))

b. cos–1(ex )
2
2
1 – (ex )2
–(ex )'
2
2
=
–2xex
1 – e2x2
2
Set u = x3, so [tan–1(x3)]' = (x3)'
1 + (x3)2 = 3x2
1 + x6
a. tan–1(x3)
–u'
1 – u2
[cos–1 (u)]' = u'
1 + u2[tan–1(u)]' =
u'
|u|u2 – 1
[sec–1(u)]' =
c. sec–1(ln(x))

b. cos–1(ex )
2
2
1 – (ex )2
–(ex )'
2
2
=
–2xex
1 – e2x2
2
Set u = ln(x), so [sec–1(ln(x)]'
=
Set u = x3, so [tan–1(x3)]' = (x3)'
1 + (x3)2 = 3x2
1 + x6
a. tan–1(x3)
–u'
1 – u2
[cos–1 (u)]' = u'
1 + u2[tan–1(u)]' =
u'
|u|u2 – 1
[sec–1(u)]' =
c. sec–1(ln(x))

b. cos–1(ex )
2
2
1 – (ex )2
–(ex )'
2
2
=
–2xex
1 – e2x2
2
c. sec–1(ln(x))
=
1/x
|ln(x)|ln2(x) – 1
Set u = x3, so [tan–1(x3)]' = (x3)'
1 + (x3)2 = 3x2
1 + x6
a. tan–1(x3)
–u'
1 – u2
[cos–1 (u)]' = u'
1 + u2[tan–1(u)]' =
u'
|u|u2 – 1
[sec–1(u)]' =

b. cos–1(ex )
2
2
1 – (ex )2
–(ex )'
2
2
=
–2xex
1 – e2x2
2
=
1/x
|ln(x)|ln2(x) – 1
= 1
x|ln(x)||ln2(x) – 1
Set u = x3, so [tan–1(x3)]' = (x3)'
1 + (x3)2 = 3x2
1 + x6
a. tan–1(x3)
–u'
1 – u2
[cos–1 (u)]' = u'
1 + u2[tan–1(u)]' =
u'
|u|u2 – 1
[sec–1(u)]' =
c. sec–1(ln(x))

= sin-1(u) + C
1 – u2
du
Expressing the relations in integrals:
∫

= sin-1(u) + C
1 – u2
du
∫
= cos-1(u) + C
1 – u2
- du
∫

= sin-1(u) + C
1 – u2
du
∫
= cos-1(u) + C
1 – u2
- du
∫
= tan-1(u) + C
du
∫ 1 + u2

= sin-1(u) + C
1 – u2
du
|u|u2 – 1
∫
= cos-1(u) + C
1 – u2
- du
∫
= tan-1(u) + C
du
∫ 1 + u2
= sec-1(u) + C∫
du

= sin-1(u) + C
1 – u2
du
∫
= cos-1(u) + C
1 – u2
- du
∫
= tan-1(u) + C
du
∫ 1 + u2
= sec-1(u) + C∫
Example B. Find the integral ∫
dx
9 + 4x2
|u|u2 – 1
du

= sin-1(u) + C
1 – u2
du
∫
= cos-1(u) + C
1 – u2
- du
∫
= tan-1(u) + C
du
∫ 1 + u2
= sec-1(u) + C∫
Match the form of the integral to the one for tan-1(u).
|u|u2 – 1
du
dx
9 + 4x2

= sin-1(u) + C
1 – u2
du
∫
= cos-1(u) + C
1 – u2
- du
∫
= tan-1(u) + C
du
∫ 1 + u2
= sec-1(u) + C∫
Write 9 + 4x2 = 9 (1 + x2)
4
9
|u|u2 – 1
du
dx
9 + 4x2

= sin-1(u) + C
1 – u2
du
∫
= cos-1(u) + C
1 – u2
- du
∫
= tan-1(u) + C
du
∫ 1 + u2
= sec-1(u) + C∫
Write 9 + 4x2 = 9 (1 + x2) = 9 [1 + ( x)2]2
3
4
9
|u|u2 – 1
du
dx
9 + 4x2

= sin-1(u) + C
1 – u2
du
∫
= cos-1(u) + C
1 – u2
- du
∫
= tan-1(u) + C
du
∫ 1 + u2
= sec-1(u) + C∫
Write 9 + 4x2 = 9 (1 + x2) = 9 [1 + ( x)2]2
3
4
9
Hence dx
9 + 4x2∫ = dx
1 + ( x)2∫
1
9 2
3
|u|u2 – 1
du
dx
9 + 4x2

dx
1 + ( x)2∫
1
9 2
3
substitution method

Set u =
dx
1 + ( x)2∫
1
9 2
3
2
3
x
substitution method

Set u =
dx
1 + ( x)2∫
1
9 2
3
2
3
x  du
dx = 2
3
substitution method

Set u =
dx
1 + ( x)2∫
1
9 2
3
2
3
x  du
dx = 2
3
So dx = 3
2
du
substitution method

Set u =
dx
1 + ( x)2∫
1
9 2
3
2
3
x  du
dx = 2
3
So dx = 3
2
du
= ∫
1
9
1
1 + u2
3
2
du
substitution method

Set u =
dx
1 + ( x)2∫
1
9 2
3
2
3
x  du
dx = 2
3
So dx = 3
2
du
= ∫
1
9
1
1 + u2
3
2
du
= ∫
1
6
1
1 + u2 du
substitution method

Set u =
dx
1 + ( x)2∫
1
9 2
3
2
3
x  du
dx = 2
3
So dx = 3
2
du
= ∫
1
9
1
1 + u2
3
2
du
= ∫
1
6
1
1 + u2 du
= tan-1(u) + C
1
6
substitution method

Set u =
dx
1 + ( x)2∫
1
9 2
3
2
3
x  du
dx = 2
3
So dx = 3
2
du
= ∫
1
9
1
1 + u2
3
2
du
= ∫
1
6
1
1 + u2 du
= tan-1(u) + C
1
6
= tan-1( x) + C
1
6
2
3
substitution method

ex
∫Example C. Find the definite integral
1 – e2x
dx
0
ln(1/2)

ex
∫Example C. Find the definite integral
1 – e2x
dx
0
ln(1/2)
ex
∫ 1 – e2x
dx
0
ln(1/2)

ex
∫
substitution method
Example C. Find the definite integral
1 – e2x
dx
0
ln(1/2)
ex
∫ 1 – e2x
dx
0
ln(1/2)

Set u =
ex
∫
substitution method
1 – e2x
dx
0
ln(1/2)
ex
ex
∫ 1 – e2x
dx
0
ln(1/2)

Set u =
ex
∫
 du
dx =
substitution method
1 – e2x
dx
0
ln(1/2)
ex ex
ex
∫ 1 – e2x
dx
0
ln(1/2)

Set u =
ex
∫
 du
dx =
So dx = du/ex
substitution method
1 – e2x
dx
0
ln(1/2)
ex ex
ex
∫ 1 – e2x
dx
0
ln(1/2)

Set u =
ex
∫
 du
dx =
So dx = du/ex
substitution method
1 – e2x
dx
0
ln(1/2)
ex ex
for x = ln(1/2)  u = 1/2
ex
∫ 1 – e2x
dx
0
ln(1/2)

Set u =
ex
∫
 du
dx =
So dx = du/ex
substitution method
1 – e2x
dx
0
ln(1/2)
ex
∫ 1 – e2x
dx
0
ln(1/2)
ex ex
for x = ln(1/2)  u = 1/2
x = 0  u = 1

Set u =
ex
∫
 du
dx =
So dx = du/ex
=
substitution method
1 – e2x
dx
0
ln(1/2)
ex
∫ 1 – e2x
dx
0
ln(1/2)
ex ex
for x = ln(1/2)  u = 1/2
x = 0  u = 1
ex
∫ 1 – u2

Set u =
ex
∫
 du
dx =
So dx = du/ex
=
substitution method
1 – e2x
dx
0
ln(1/2)
ex
∫ 1 – e2x
dx
0
ln(1/2)
ex ex
for x = ln(1/2)  u = 1/2
x = 0  u = 1
ex
∫ 1 – u2
du
ex

Set u =
ex
∫
 du
dx =
So dx = du/ex
=
substitution method
1 – e2x
dx
0
ln(1/2)
ex
∫ 1 – e2x
dx
0
ln(1/2)
ex ex
for x = ln(1/2)  u = 1/2
x = 0  u = 1
ex
∫ 1 – u2
du
1
1/2
ex

Set u =
ex
∫
 du
dx =
So dx = du/ex
=
substitution method
1 – e2x
dx
0
ln(1/2)
ex
∫ 1 – e2x
dx
0
ln(1/2)
ex ex
for x = ln(1/2)  u = 1/2
x = 0  u = 1
ex
∫ 1 – u2
du
1
1/2
ex
= ∫ 1 – u2
du
1
1/2

Set u =
ex
∫
 du
dx =
So dx = du/ex
=
substitution method
1 – e2x
dx
0
ln(1/2)
ex
∫ 1 – e2x
dx
0
ln(1/2)
ex ex
for x = ln(1/2)  u = 1/2
x = 0  u = 1
ex
∫ 1 – u2
du
1
1/2
ex
= ∫ 1 – u2
du
1
1/2
= sin-1(u) |
1/2
1

Set u =
ex
∫
 du
dx =
So dx = du/ex
=
substitution method
1 – e2x
dx
0
ln(1/2)
ex
∫ 1 – e2x
dx
0
ln(1/2)
ex ex
for x = ln(1/2)  u = 1/2
x = 0  u = 1
ex
∫ 1 – u2
du
1
1/2
ex
= ∫ 1 – u2
du
1
1/2
= sin-1(u) |
1/2
1
= sin-1(1) – sin-1(1/2)

Set u =
ex
∫
 du
dx =
So dx = du/ex
=
substitution method
1 – e2x
dx
0
ln(1/2)
ex
∫ 1 – e2x
dx
0
ln(1/2)
ex ex
for x = ln(1/2)  u = 1/2
x = 0  u = 1
ex
∫ 1 – u2
du
1
1/2
ex
= ∫ 1 – u2
du
1
1/2
= sin-1(u) |
1/2
1
= sin-1(1) – sin-1(1/2) = π/2 – π/6

Set u =
ex
∫
 du
dx =
So dx = du/ex
=
substitution method
1 – e2x
dx
0
ln(1/2)
ex
∫ 1 – e2x
dx
0
ln(1/2)
ex ex
for x = ln(1/2)  u = 1/2
x = 0  u = 1
ex
∫ 1 – u2
du
1
1/2
ex
= ∫ 1 – u2
du
1
1/2
= sin-1(u) |
1/2
1
= sin-1(1) – sin-1(1/2) = π/2 – π/6 = π/3

Lastly, we have the hyperbolic trigonometric
functions.

functions. These functions are made from the
exponential functions with relations among
them that are similar to the trig-family.

We define the hyperbolic sine as
sinh(x) = (pronounced as "sinch of x").
ex – e-x
2

sinh(x) = (pronounced as "sinch of x")
We define the hyperbolic cosine as
cosh(x) = (pronounced as "cosh of x")
ex – e-x
2
ex + e-x
2

sinh(x) = (pronounced as "sinch of x")
We define the hyperbolic cosine as
cosh(x) = (pronounced as "cosh of x")
ex – e-x
2
ex + e-x
2
We define the hyperbolic tangent, cotangent,
secant and cosecant as in the trig-family.

The hyperbolic tangent:
tanh(x) =
sinh(x)
cosh(x) =
ex – e-x
ex + e-x
The hyperbolic cotangent:
coth(x) =
cosh(x)
sinh(x) =
ex – e-x
ex + e-x
The hyperbolic secant:
sech(x) =
1
cosh(x) =
ex + e-x
2
The hyperbolic cosecant:
csch(x) =
1
sinh(x) =
ex – e-x
2

3,11,12,33,77,78,82,89,90.

As with the trig-family, we have the hyperbolic-
trig hexagram to help us with their relations.

Hyperbolic Trig
Hexagram
sinh(x)cosh(x)
coth(x)
csch(x)
tanh(x)
sech(x)
1
co-side
As with the trig-family, we have the hyperbolic-
trig hexagram to help us with their relations.

sinh(x)cosh(x)
coth(x)
csch(x)
tanh(x)
sech(x)
1
Starting from any
position, take two
steps without
turning, we have
I =
II
III

sinh(x)cosh(x)
coth(x)
csch(x)
tanh(x)
sech(x)
1
Starting from any
position, take two
steps without
turning, we have
I =
II
III
For example, staring at cosh(x), go to sinh(x)
then to tanh(x),

sinh(x)cosh(x)
coth(x)
csch(x)
tanh(x)
sech(x)
1
Starting from any
position, take two
steps without
turning, we have
I =
II
III
then to tanh(x), we get the relation
cosh(x) = sinh(x)
tanh(x)

sinh(x)cosh(x)
coth(x)
csch(x)
tanh(x)
sech(x)
1
Starting from any
position, take two
steps without
turning, we have
I =
II
III
then to tanh(x), we get the relation
cosh(x) = , similarly sech(x) =sinh(x)
tanh(x)
csch(x)
coth(x)

sinh(x)cosh(x)
coth(x)
csch(x)
tanh(x)
sech(x)
1
Square-difference
Relations:

sinh(x)cosh(x)
coth(x)
csch(x)
tanh(x)
sech(x)
1
Square-difference
Relations:
The three upside
down triangles give
the sq-differernce
relations.

sinh(x)cosh(x)
coth(x)
csch(x)
tanh(x)
sech(x)
1
Square-difference
Relations:
The three upside
down triangles give
the sq-differernce
relations.
The difference of
the squares on top
is the square of the
bottom one.

sinh(x)cosh(x)
coth(x)
csch(x)
tanh(x)
sech(x)
1
Square-difference
Relations:
The three upside
down triangles give
the sq-differernce
relations.
The difference of
the squares on top
bottom one.
cosh2(x) – sinh2(x) = 1

sinh(x)cosh(x)
coth(x)
csch(x)
tanh(x)
sech(x)
1
Square-difference
Relations:
The three upside
down triangles give
the sq-differernce
relations.
The difference of
the squares on top
bottom one.
coth2(x) – 1 = csch2(x)

sinh(x)cosh(x)
coth(x)
csch(x)
tanh(x)
sech(x)
1
Square-difference
Relations:
The three upside
down triangles give
the sq-differernce
relations.
The difference of
the squares on top
bottom one.
coth2(x) – 1 = csch2(x)
1 – tanh2(x) = sech2(x)

Hyperbolic trig-functions show up in
engineering.

engineering. Specifically the graph y = cosh(x)
gives the shape of a hanging cable.

Graph of y = cosh(x)
engineering. Specifically the graph y = cosh(x)
gives the shape of a hanging cable.
(0, 1)

The derivatives of the hyperbolic trig-functions
are similar, but not the same as, the trig-family.

One may easily check that:
[sinh(x)]' = cosh(x)
[cosh(x)]' = sinh(x)

[tanh(x)]' = sech2(x)
[coth(x)]' = -csch2(x)

[sech(x)]' = -sech(x)tanh(x)
[csch(x)]' = -csch(x)coth(x)

F
r
a
n
k
M
a
2
0
0
6

[sech(x)]' = -sech(x)tanh(x)
[csch(x)]' = -csch(x)coth(x)
HW. Write down the chain–rule versions of the
derivatives of the hyperbolic trig-functions.

12 derivatives and integrals of inverse trigonometric functions x

Recommended

Recommended

More Related Content

What's hot

What's hot (20)

Similar to 12 derivatives and integrals of inverse trigonometric functions x

Similar to 12 derivatives and integrals of inverse trigonometric functions x (20)

More from math266

More from math266 (20)

Recently uploaded

Recently uploaded (20)

12 derivatives and integrals of inverse trigonometric functions x