Download as PDF, PPTX
Uploaded byUniversità Cattolica del Sacro Cuore
Le leve
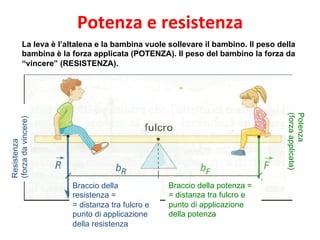
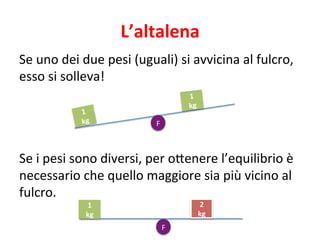
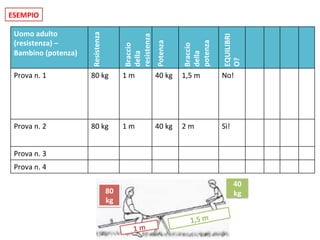
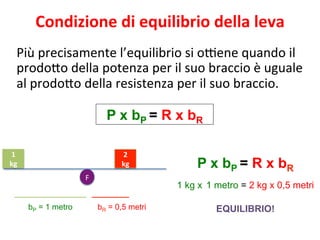
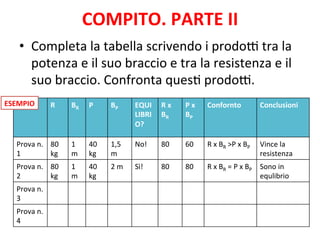
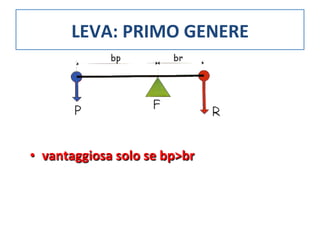
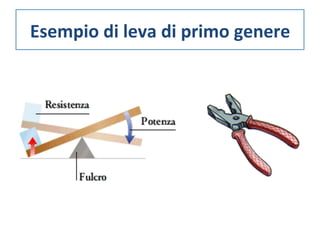
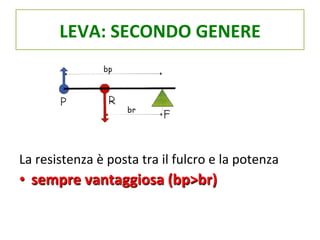
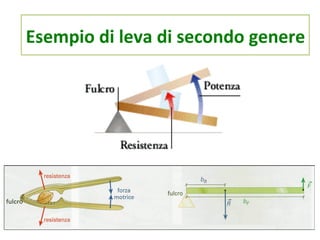
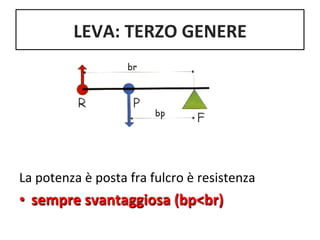
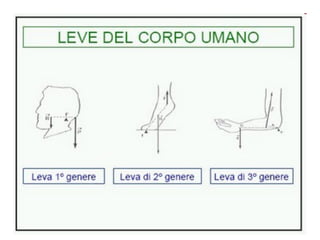
Il documento tratta delle leve, strumenti meccanici per modificare l'azione di una forza tramite aste rigide che ruotano attorno a un fulcro. Viene spiegato come l'equilibrio tra potenza e resistenza dipenda dalle distanze dal fulcro e vengono presentati vari tipi di leve (primo, secondo e terzo genere) e le loro condizioni di vantaggio. Infine, si propone un esperimento per verificare il principio e si forniscono formule e tabelle per documentare i risultati.
![Le leve [prof. santi caltabiano]](https://cdn.slidesharecdn.com/ss_thumbnails/leleveprof-190913154613-thumbnail.jpg?width=640&height=640&fit=bounds)
Le leve
- 1.
- 2. LE LEVE •Macchine semplici, usate per modificare l’azione di una forza. • Si tra9a di aste rigide, che ruotano a9orno a un punto fisso, il fulcro
- 3. Potenza e resistenza La leva è l’altalena e la bambina vuole sollevare il bambino. Il peso della bambina è la forza applicata (POTENZA). Il peso del bambino la forza da “vincere” (RESISTENZA). Potenza (forza applicata) Resistenza (forza da vincere) Braccio della potenza = = distanza tra fulcro e punto di applicazione della potenza Braccio della resistenza = = distanza tra fulcro e punto di applicazione della resistenza
- 4. L’altalena Un esempio di leva è l’altalena. L’altalena è in equilibrio se i pesi sono uguali e le distanze dal fulcro sono uguali. F 1 kg 1 kg
- 5. L’altalena Se uno dei due pesi (uguali) si avvicina al fulcro, esso si solleva! F 1 kg 1 kg Se i pesi sono diversi, per o9enere l’equilibrio è necessario che quello maggiore sia più vicino al fulcro. F 2 kg 1 kg
- 6. • Realizza COMPITO. PARTE I un esperimento per verificare quanto scri9o nella slide precedente (uGlizza una bilancia per scoprire il peso dell’ogge9o e il metro per trovare la distanza dal fulcro). • UGlizza sempre gli stessi oggeH, ma spostali per effe9uare 4 prove diverse. • Documenta quello che hai verificato con una tabella (vedi esempio nella prossima slide) e una fotografia (o un disegno).
- 7. Uomo adulto (resistenza) – Bambino (potenza) Resistenza Braccio della resistenza Potenza Braccio della potenza EQUILIBRI O? Prova n. 1 80 kg 1 m 40 kg 1,5 m No! Prova n. 2 80 kg 1 m 40 kg 2 m Sì! Prova n. 3 Prova n. 4 80 kg 40 kg m 1,5 1 m ESEMPIO
- 8. Condizione di equilibrio della leva Più precisamente l’equilibrio si oHene quando il prodo9o della potenza per il suo braccio è uguale al prodo9o della resistenza per il suo braccio. P x bP = R x bR F 2 kg 1 kg bP = 1 metro bR = 0,5 metri P x bP = R x bR 1 kg x 1 metro = 2 kg x 0,5 metri EQUILIBRIO!
- 9. COMPITO. PARTE II • Completa la tabella scrivendo i prodoH tra la potenza e il suo braccio e tra la resistenza e il suo braccio. Confronta quesG prodoH. R BR P BP EQUI LIBRI O? R x BR P x BP Confornto Conclusioni ESEMPIO Prova n. 1 80 kg 1 m 40 kg 1,5 m No! 80 60 R x BR >P x BP Vince la resistenza Prova n. 2 80 kg 1 m 40 kg 2 m Sì! 80 80 R x BR = P x BP Sono in equlibrio Prova n. 3 Prova n. 4
- 10. Leve vantaggiose Una leva è vantaggiosa se la potenza è minore della resistenza, cioè se P<R (vuol dire che riesco a sollevare un ogge9o più pensante della forza che io applico). La formula P x bP = R x bR equivale a: P/R = bR/bP. Quindi una leva è vantaggiosa se P/R è una frazione propria. Allora anche bR/bP lo è. Perciò una leva è vantaggiosa se bP>bR.
- 11. Tipi di leve Ci sono tre Gpi di leve a seconda della posizione reciproca di fulcro (F), punto di applicazione della potenza (P) e punto di applicazione della resistenza (R): • I genere: PFR • II genere: PRF • III genere: RPF
- 12. LEVA: PRIMO GENERE Il fulcro si trova tra potenza e resistenza
- 13. LEVA: PRIMO GENERE • vantaggiosa solo se bp>br
- 14. Esempio di leva di primo genere
- 15. LEVA: SECONDO GENERE La resistenza è posta tra il fulcro e la potenza • sempre vantaggiosa (bp>br)
- 16. Esempio secondo genere: Esempio dINi TleEvRaRE dSIiS sTeENcoTIn do genere
- 17. LEVA: TERZO GENERE La potenza è posta fra fulcro è resistenza • sempre svantaggiosa (bp<br)
- 18. EsEesmepmiop itoe rdzoi lgeevnae drei :t IeNrTzEoR gPeOnTeErNeT I
- 19. Tipi di leve e vantaggio Riassumendo: • una leva di I genere può essere vantaggiosa o svantaggiosa… è vantaggiosa se bP>bR; • una leva di II genere è sempre vantaggiosa; • una leva di III genere è sempre svantaggiosa.