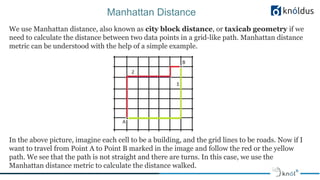
Machine learning is presented by Pranay Rajput. The agenda includes an introduction to machine learning, basics, classification, regression, clustering, distance metrics, and use cases. ML allows computer programs to learn from experience to improve performance on tasks. Supervised learning predicts labels or targets while unsupervised learning finds hidden patterns in unlabeled data. Popular algorithms include classification, regression, and clustering. Classification predicts class labels, regression predicts continuous values, and clustering groups similar data points. Distance metrics like Euclidean, Manhattan, and cosine are used in ML models to measure similarity between data points. Common applications involve recommendation systems, computer vision, natural language processing, and fraud detection. Popular frameworks for ML include scikit-learn, TensorFlow, Keras

1. Introduction to Machine Learning
Presented By:-
Pranay Rajput
Software Consultant- AI/ML

2. Lack of etiquette and manners is a huge turn off.
KnolX Etiquettes
Punctuality
Respect Knolx session timings,
you are requested not to join
sessions after a 5 minutes
threshold post the session start
time.
Feedback
Make sure to submit a
constructive feedback for all
sessions as it is very helpful for
the presenter.
Silent Mode
Keep your mobile devices in
silent mode, feel free to move
out of session in case you need
to attend an urgent call.
Avoid Disturbance
Avoid unwanted chit chat during
the session.

3. • Introduction
• Basics
• Classification
• Regression
• Clustering
• Distance Metrics
• Use-Cases
Agenda

4. What is AI?
In computer science, the term artificial intelligence (AI) refers to any human-like intelligence exhibited by a
computer, robot, or other machine. In popular usage, artificial intelligence refers to the ability of a computer or
machine to mimic the capabilities of the human mind—learning from examples and experience, recognizing
objects, understanding and responding to language, making decisions, solving problems—and combining these
and other capabilities to perform functions a human might perform, such as greeting a hotel guest or driving a
car.
What is ML?
A computer program is said to learn from experience (E) with some class of tasks (T) and a performance
measure (P) if its performance at tasks in T as measured by P improves with E.

6. Terminology
• Features– The number of features or distinct traits that can be used to describe each item
in a quantitative manner.
• Samples – A sample is an item to process (e.g. classify). It can be a document, a picture,
a sound, a video, a row in database or CSV file, or whatever you can describe with a fixed
set of quantitative traits.
• Feature vector – It is an n-dimensional vector of numerical features that represent some
object.
• Feature extraction – Transforms the data in the high-dimensional space to a space of
fewer dimensions.
• Training/Evolution set – Set of data to discover potentially predictive relationships.

7. Let’s dig deep into it...
What do you mean by
Apple

9. WorkFlow

11. Supervised vs Unsupervised vs Reinforcement

12. • Classification: Classification is a type of supervised machine learning algorithm. For any
given input, the classification algorithms help in the prediction of the class of the output variable.
There can be multiple types of classifications like binary classification, multi-class classification,
etc.
• Regression: Regression is a type of supervised machine learning algorithm.It predicts
continuous valued output.The Regression analysis is the statistical model which is used to predict
the numeric data instead of labels.
• Clustering: Clustering is a type of unsupervised machine learning algorithm. It is used to
group data points having similar characteristics as clusters. Ideally, the data points in the same
cluster should exhibit similar properties and the points in different clusters should be as dissimilar
as possible.
Techniques

13. ➢ Classify a document into a predefined category.
➢ Documents can be text, images
➢ Popular one is Naive Bayes Classifier.
➢ Steps:
– Step1 : Train the program (Building a Model) using a training set with a
category for e.g. sports, cricket, news,
– Classifier will compute probability for each word, the
probability that it makes a document belong to each of
considered categories
– Step2 : Test with a test data set against this Model
Classification

14. ● It is a measure of the relation between the mean value of one variable (e.g.output) and
corresponding values of other variables (e.g. time and cost).
● Regression analysis is a statistical process for estimating the relationships among
variables.
● Regression means to predict the output value using training data.
Regression

15. • Clustering is the task of grouping a set of objects in such a way that objects in the
same group (called a cluster) are more similar to each other.
• For e.g. these keywords
– “man’s shoe”
– “women’s shoe”
– “women’s t-shirt”
– “man’s t-shirt”
– can be cluster into 2 categories “shoe” and “t-shirt” or
“man” and “women”
• Popular ones are K-means clustering
and Hierarchical clustering
Clustering

16. • Method of cluster analysis which seeks to build a hierarchy of clusters.
• There can be two strategies:-
– Agglomerative:
• This is a "bottom up" approach: each observation starts in its own cluster, and pairs of clusters are
merged as one moves up the hierarchy.
• Time complexity is O(n^3)
– Divisive:
• This is a "top down" approach: all observations
start in one cluster, and splits are performed
recursively as one moves down the hierarchy.
• Time complexity is O(2^n)
Hierarchical clustering

17. Partitional clustering decomposes a data set into a set of disjoint clusters. Given a data set of N
points, a partitioning method constructs K (N ≥ K) partitions of the data, with each partition
representing a cluster. That is, it classifies the data into K groups by satisfying the following
requirements: (1) each group contains at least one point, and (2) each point belongs to
exactly one group.
Partitional Clustering

18. • Example of partitional clustering.
• Partition n observations into k clusters in which each observation belongs to the cluster
with the nearest mean, serving as a prototype of the cluster.
K-means Clustering

20. Some distance metrics used in machine
learning models

21. To define Minkowski Distance,we need to learn some mathematical terms.They include the followings:
● Vector space: It is a collection of objects called vectors that can be added together and multiplied by numbers (also called
scalars).
● Norm: A norm is a function that assigns a strictly positive length to each vector in a vector space (The only exception is the zero
vector whose length is zero).It is usually represented as ∥x∥.
● Normed vector space : It is a vector space over the real or complex numbers on which a norm is defined.
Minkowski distance is defined as the similarity metric between two points in the normed vector space.It is represented by the formula,
Minkowski Distance

22. It represents also a generalized metric that includes Euclidean and Manhattan distance.We can manipulate the
value of p and calculate the distance in three different ways which is also known as Lp form.
p = 1, Manhattan Distance
p = 2, Euclidean Distance
p = ∞, Chebyshev Distance
Where it is used- Minkowski distance is frequently used when the variables of interest are measured on ratio
scales with an absolute zero value.

23. Manhattan Distance
We use Manhattan distance, also known as city block distance, or taxicab geometry if we
need to calculate the distance between two data points in a grid-like path. Manhattan distance
metric can be understood with the help of a simple example.
In the above picture, imagine each cell to be a building, and the grid lines to be roads. Now if I
want to travel from Point A to Point B marked in the image and follow the red or the yellow
path. We see that the path is not straight and there are turns. In this case, we use the
Manhattan distance metric to calculate the distance walked.

24. Note: - In high dimensional data Manhattan distance is preferred. Also, if you are calculating errors, Manhattan Distance is
useful when you want to emphasis on outliers due to its linear nature.
We can get the equation for Manhattan distance by substituting p = 1 in the
Minkowski distance formula. The formula is:-

25. Euclidean Distance
Euclidean distance is the straight line distance between 2 data points in a
plane.It is calculated using the Minkowski Distance formula by setting ‘p’
value to 2, thus, also known as the L2 norm distance metric. The formula
is:-
Note:- Euclidean distance does not perform well for high dimensional data. This occurs due to the ‘curse of dimensionality’.

26. Hamming Distance:
Hamming distance is a metric for comparing two binary data strings. While comparing two binary strings of equal length,
Hamming distance is the number of bit positions in which the two bits are different.
The Hamming distance between two strings, a and b is denoted as d(a,b).
In order to calculate the Hamming distance between two strings, and, we perform their XOR operation, (a⊕ b), and then count
the total number of 1s in the resultant string.
Suppose there are two strings 11011001 and 10011101.
11011001 ⊕ 10011101 = 01000100. Since, this contains two 1s,
the Hamming distance, d(11011001, 10011101) = 2.

27. Cosine Distance & Cosine Similarity:
Cosine distance & Cosine Similarity metric is mainly used to find similarities between two data points. As the cosine distance
between the data points increases, the cosine similarity, or the amount of similarity decreases, and vice versa. Thus, Points
closer to each other are more similar than points that are far away from each other. Cosine similarity is given by Cos θ, and
cosine distance is 1- Cos θ. Example:-
In the above image, there are two data points shown in blue, the angle between these points is 90 degrees, and Cos 90 = 0.
Therefore, the shown two points are not similar, and their cosine distance is 1 — Cos 90 = 1.

28. Machine learning: when ?
➢ Learning is useful when:
- Human expertise does not exist (navigating on Mars),
- Humans are unable to explain their expertise (speech recognition)
- Solution changes in time (routing on a computer network)
- Solution needs to be adapted to particular cases (user biometrics)
Example: It is easier to write a program that learns to play checkers or
backgammon well by self-play rather than converting the expertise of a master
player to a program.

29. ● Machine Translation (Language Translation)
● Image Search (Similarity)
● Recommendation System : Amazon prime,Netflix
● Classification : Google News,Spam Email Detection
● Text Summarization - Google News
● Rating a Review/Comment: Yelp
● Fraud detection : Credit card Providers
● Decision Making : e.g. Bank/Insurance sector
● Sentiment Analysis : Crime Detection
● Speech Recognition – Alexa,Siri,Cortana,Google Home
● Face Detection – Facebook’s Photo tagging
Use-Cases

30. ● Weka
● Carrot2
● Gate
● OpenNLP
● LingPipe
● Stanford NLP
● Mallet – Topic Modelling
● Gensim – Topic Modelling (Python)
● Apache Mahout
● MLlib – Apache Spark
● scikit-learn - Python
● LIBSVM : Support Vector Machines
and many more...
Popular Frameworks/Tools

31. Thank You !