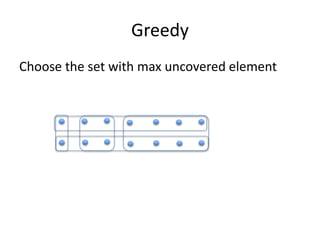
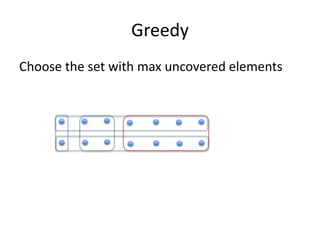
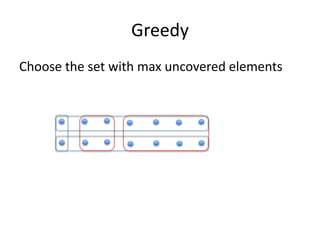
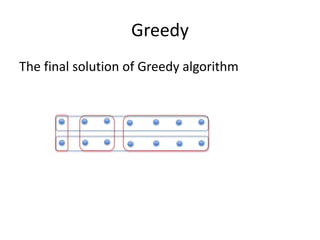
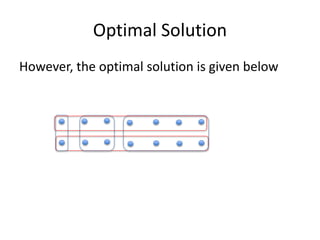
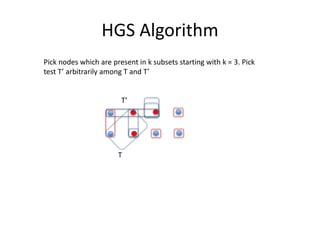
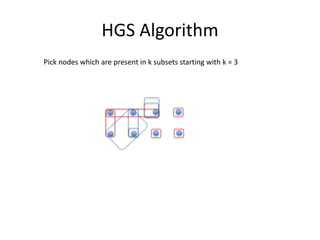
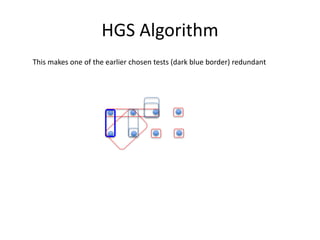
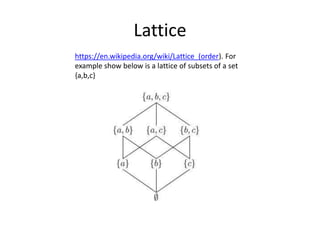
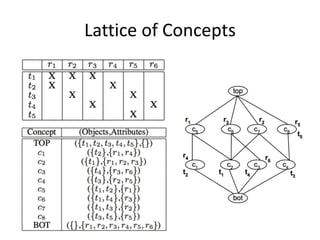
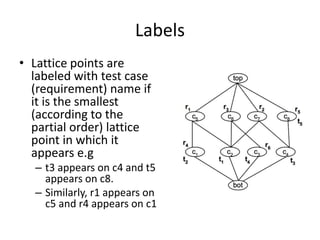
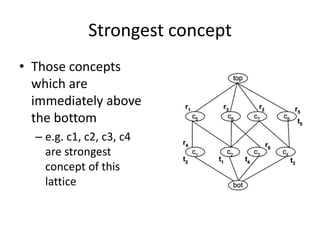
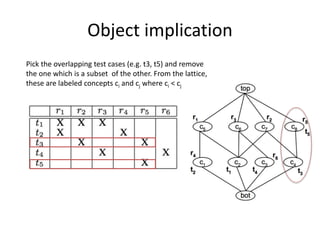
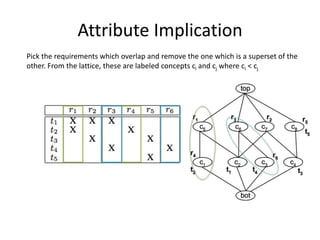
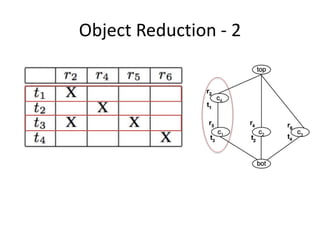
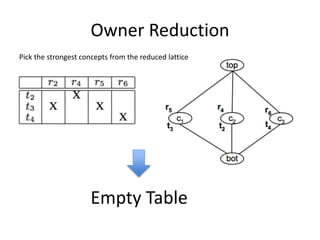
The document presents a greedy algorithm for test suite minimization aimed at reducing the number of tests run on large software systems by eliminating redundant test cases. It defines a problem where tests cover multiple requirements, and provides a method to identify the minimum set of tests needed to satisfy all requirements using a test-requirement matrix. The proposed solution leverages delayed greedy algorithms and concept analysis to optimize test selection, ultimately addressing the NP-hard nature of the problem.

1. Test Suite Minimization
A Concept Analysis Inspired Greedy
Algorithm for Test Suite
Minimization
http://llvm.org/pubs/2005-09-PASTE-GreedySuiteMinimization.pdf

2. Motivation
• Large softwares typically have large number of
tests and their complete runs take several hours
• For minimal changes a complex software
undergoes daily, a lot of these tests are only
testing what’s already tested
• These tests are run in nightly release process, for
pre-check in requirements and check-ins
consuming time, energy and dollars

3. Problem
• How do we know which tests to run given a
software change?
– Test coverage information for each tests can
answer this question
• But we can do better. Do we need to run all
the tests according to the test coverage?
– But this problem is hard. NP-hard.

4. Problem in an example
public boolean isWeekend(int day) {
if(day > 5) {
return false; //R1
} else {
return true; //R2
}
}
Test/Req R1 R2 R3
T1 X X
T2 X
T3 X X
//T1
public void testIsWeekend(int ) {
AssertFalse(isWeekend(Friday.index))//5
AssertTrue(isWeekend(Saturday.index))//6
}
//T2
public void testIsBefore() {
AssertTrue(isBefore(Monday.index,
Friday.index));
}
//T3
public void testMonday() {
AssertFalse(isWeekend(Monday.index))//5
AssertTrue(isBefore(Monday.index,
Friday.index));
}
public boolean isBefore(int day1, int
day2) {
return day1 < day2 //R3
}

5. Problem in an example
• Let us consider two functions:
– IsWeekend: If days are numbered from Monday to Sunday, every day
numbered less than 5 is a weekday, otherwise it’s a weekend. These
are marked as requirements R1 and R2 respectively
– IsBefore checks if day1 comes before day2 and is our requirement R3
• Now also consider 3 test cases
– T1 tests if Friday and Saturday is a Weekend day
– T2 tests if Monday comes before Friday
– T3 tests if Monday is weekend and comes before Friday.
• Let us also create a table to map which tests which of the
requirements. Now from the table we can see that if I run T1 and
T2, the T3 is redundant. If Friday is a weekday and Monday comes
before Friday then Monday has to be a weekday

6. Problem Definition
• Given a test-requirement matrix where
– A test tests all the requirements listed against it
– A requirement may be satisfied by any test listed
against it
• Find the minimum number of tests which can
test all the requirements

7. Outline
• Problem is NP Hard – Reducible from Set
Cover
• Heuristics used to solve this problem
– Greedy
– HGS Algorithm
• Delayed Greedy Algorithm using Concept
Analysis (this algorithm)

8. NP Hard
If there are n different things, how many subsets
of n can I create?
2n
Therefore, if there are n tests, how many tests
should I run to have enough coverage?

9. Convention
• In the following slides, circles denote
requirements and the rectangles denote tests
– Rectangles span multiple circles. This implies that
a test can test multiple requirements
• A requirement can be completely tested by
any test in which it appears.
• Red rectangles represent selected tests

10. Greedy Algorithm
• Assuming the given requirements and tests,
Greedy algorithm tries to pick the smallest set
of test cases
• To achieve this, Greedy algorithm choses a
test case which covers the maximum number
of requirements. It then removes the covered
requirements and test from consideration
• The algorithm ends when no requirements are
left

11. Greedy
Choose the set with max uncovered element

12. Greedy
Choose the set with max uncovered elements

13. Greedy
Choose the set with max uncovered elements

14. Greedy
The final solution of Greedy algorithm

15. Optimal Solution
However, the optimal solution is given below

16. Problem with Greedy?
• The algorithm missed the optimal solution.
Why?
• Choice about picking the first set was made
too early!

17. HGS Algorithm
• Choose requirements which are covered by k
tests cases starting with k = 1
• Pick the test case which covers the most
requirements. If more than one tests qualify
then pick randomly
• Remove the requirements by the picked test.
Continue with the rest

18. HGS Algorithm
Pick requirements which are tested by k tests. k = 1

19. HGS Algorithm
Pick requirements which are tested by k tests. k = 1

20. HGS Algorithm
Pick requirements which are tested by k tests. k = 2

21. HGS Algorithm
Pick requirements which are tested by k tests. k = 2

22. HGS Algorithm
Pick nodes which are present in k subsets starting with k = 3. Pick
test T’ arbitrarily among T and T’
T
T’

23. HGS Algorithm
Pick nodes which are present in k subsets starting with k = 3

24. HGS Algorithm
Now find the remaining requirement (shown as red circle). Pick a
test randomly which satisfies it

25. HGS Algorithm
Pick nodes which are present in k subsets starting with k = 3.
Picked a test randomly among the three

26. HGS Algorithm
This makes one of the earlier chosen tests (dark blue border) redundant

27. Problem with HGS?
Implications could not be derived while making
choices

28. Problems with other Heuristics
• Choice about picking the first set was made
too early
• Implications could not be derived

29. How Concept Analysis works?
Find and eliminate all the dependencies before choosing subsets

30. How Concept Analysis works?
t3 tests requirements r2 and r5. While t5 tests r5 only. Therefore if t3 is run, t5 can
be ignored

31. How Concept Analysis works?
If r4 is tested, then r1 is tested also. Similarly, r6 and r3

32. How Concept Analysis works?
Remove r1, r3 and t5

33. How Concept Analysis works?
Similarly, t1 can be removed in favor of t3

34. How Concept Analysis works?
Now apply Greedy minimum set cover algorithm on that rest to find
the minimum number of tests to be run to test all the requirements

35. How Concept Analysis works?
• Minimization of test-requirement matrix to
remove redundancies
• Delayed sub-set selection to avoid picking sub-
optimal tests
• Delayed Greedy algorithm performs at least
as well as the Greedy algorithm

36. Concept Analysis - Details
• Lattice
• Concepts
• Lattice of Concepts
• Labels
• Strong concept
• Algorithm

37. Lattice
https://en.wikipedia.org/wiki/Lattice_(order). For
example show below is a lattice of subsets of a set
{a,b,c}

38. Concept
• Consider an ordered pair (t, r) where t is the set of tests
and r is a set of requirements
• Such a set is called maximal grouping if t(or r) is the
maximal set of tests(or requirements) related to all
requirements(or tests) in r(or t)
– i.e. t = ∩iri where ri ∈ r and ri is a collection of tests from
reqruiements-test table.
– i.e. r = ∩iti where ti ∈ t and ti is a collection of tests from
requirements-test table.
• Then this maximal grouping (t, r) is called Concept

39. Lattice of Concepts

40. Lattice of Concepts
• The lattice is ordered from top to bottom for tests
i.e. at each level from top to bottom, number of
tests in the concept increases
• And from bottom to top for requirements i.e. at
each level from bottom to top, number of
requirements in the concept increases
• Not all the points of the concept lattice have a
maximal requirement set and therefore, not all of
them will be found on the CA lattice e.g. {t5}

41. Labels
• Lattice points are
labeled with test case
(requirement) name if
it is the smallest
(according to the
partial order) lattice
point in which it
appears e.g
– t3 appears on c4 and t5
appears on c8.
– Similarly, r1 appears on
c5 and r4 appears on c1

42. Strongest concept
• Those concepts
which are
immediately above
the bottom
– e.g. c1, c2, c3, c4
are strongest
concept of this
lattice

43. Object implication
Pick the overlapping test cases (e.g. t3, t5) and remove
the one which is a subset of the other. From the lattice,
these are labeled concepts ci and cj where ci < cj

44. Attribute Implication
Pick the requirements which overlap and remove the one which is a superset of the
other. From the lattice, these are labeled concepts ci and cj where ci < cj

45. Object Reduction - 2

46. Owner Reduction
Empty Table
Pick the strongest concepts from the reduced lattice

47. Delayed Greedy Algorithm
• Repeat until table is empty
– Repeat until table changes
• Object Implication
• Attribute Implication
• Owner Reduction and choose strongest concepts
– One step of Greedy

48. Experiments
• No such requirement-test matrix exists for
most softwares. How can this approach be
tested?
• Requirements: Branches and def-use pairs
(using LLVM)
• Tests: Identify tests which hit these
requirements

49. Summary
• Minimization of test-
requirement matrix to remove
redundancies
• Delayed sub-set selection to
avoid picking sub-optimal tests
• Greedy Algorithm on the
remaining table
• Never performs worse than
other approximation
algorithms.
• Minimize the number of tests to
run for a given set of
requirements
• The problem is NP hard. However,
calculation needs to be done only
once.
• Given a minimized requirement-
test matrix, changes to a
requirement will need only
limited tests to be run
Problem Solution – Delayed Greedy Algo