여러 샘플들을 참고하다 보니, tensorflow를 사용하지 않는 경우에는 직접 gradient를 계산하여 back propagation을 하도록 구현한 코드가 많다. 내가 직접 구현할 필요는 없더라도, 좀 더 명확하게 이해할 필요는 있을 것 같아서 cn231n note에서 제공하는 코드와 설명을 정리. http://blog.naver.com/freepsw/220928184473 http://cs231n.github.io/neural-networks-case-study/ 참고 데이터를 작게 생성하여, 직접 코드와 생성된 데이터를 확인하면서 좀 더 직관적으로 이해하는 과정으로 정리하다보니, 코드보다 설명이 더 많다... 아직도 명확하지는 않지만 나름대로 정리는 되었다.

1. Code로 이해하는 Back
propagation
CS231n 강좌에서 Python code로 잘 설명된 자료를 이용하여,
직접 디버깅한 결과를 보면서 Back propagation 이해하기
http://cs231n.github.io/neural-networks-case-study/
2017.03
freepsw

2. Minimal 2D toy data example 활용
아래 2개의 모델에서
Ø 어떻게 loss를 계산하고,
Ø Loss를 줄이기 위한 gradient 계산방식과
Ø 이를 모든 파라미터(W, b)에 역전파하여 최적화하는 것을 자세하게 확인
• Logistic Regression (softmax) 모델
• Neural Network 모델

3. Logistic Regression (softmax)
Back Propagation 이해

4. 1) Data set 준비
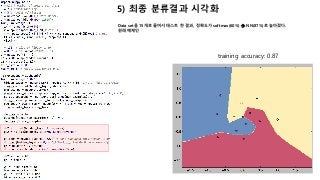
문제를 해결할 데이터 셋을 생성한다.
전체 30개의 point가 있고, 이를 3가지로 분류한다. (0, 1, 2)로 분류
정답은 y에 저장(30개에 대한 정답)
X : (15, 2)
y : (15,1)
num_examples : 15
W : (2, 3)
b : (1, 3)
[[ 0. 0. ]
[ 0.191619 0.16056824]
[ 0.43301623 -0.24999388]
[ 0.19190666 -0.7250323 ]
[-0.74941044 -0.66210573]
[-0. -0. ]
[-0.23912461 0.07293436]
[-0.1313341 0.48244311]
[ 0.47422789 0.58104037]
[ 0.99330492 -0.115522 ]
[ 0. -0. ]
[ 0.09798095 -0.22999942]
[-0.18195402 -0.46571744]
[-0.73955213 -0.12475035]
[-0.75489743 0.65584287]]
X
[0 0 0 0 0 1 1 1 1 1 2 2 2 2 2]y
[[-0.00911365 0.00989886 0.00200746]
[-0.00616948 0.00392478 0.00670659]]
[[ 0. 0. 0.]]
W
b
• 생성된 데이터를 보면,
• 선형으로 3가지를 분류하는것은 거의 불가
능해 보인다.
• XOR 문제

5. 2) 항목별 score 계산 à 예측에 대한 loss 계산
선형함수를 이용하여 15개 데이터의 score를 계산한다.
à scores = np.dot(X, W) + b # shape(15, 3)
[[ 0.00000000e+00 0.00000000e+00 0.00000000e+00]
[ -2.73697107e-03 2.52700382e-03 1.46153308e-03]
[ -2.40402494e-03 3.30519479e-03 -8.07342618e-04]
[ 2.72410403e-03 -9.45935139e-04 -4.47724846e-03]
[ 1.09147128e-02 -1.00169251e-02 -5.94488411e-03]
[ 0.00000000e+00 0.00000000e+00 0.00000000e+00]
[ 1.72933044e-03 -2.08080898e-03 9.10717959e-06]
[ -1.77949135e-03 5.93425221e-04 2.97189953e-03]
[ -7.90666446e-03 6.97476890e-03 4.84879352e-03]
[ -8.33992094e-03 9.37918452e-03 1.21926332e-03]
[ 0.00000000e+00 0.00000000e+00 0.00000000e+00]
[ 5.26013381e-04 6.72024569e-05 -1.34581859e-03]
[ 4.53150040e-03 -3.62897478e-03 -3.48864134e-03]
[ 7.50966318e-03 -7.81033793e-03 -2.32127218e-03]
[ 2.83365892e-03 -4.89858294e-03 2.88304077e-03]]
계산된 score에 softmax 함수를 적용하여 각 항목별로 정답일 확률을 계산한다.
à exp_scores = np.exp(scores)
à probs = exp_scores / np.sum(exp_scores, axis=1, keepdims=True)
[[ 0.33333333 0.33333333 0.33333333]
[ 0.33228275 0.33403649 0.33368077]
[ 0.33252159 0.33442546 0.33305295]
[ 0.33454201 0.33331648 0.33214151]
[ 0.33754504 0.3305531 0.33190187]
[ 0.33333333 0.33333333 0.33333333]
[ 0.33394798 0.33267801 0.33337401]
[ 0.33254206 0.33333209 0.33412585]
[ 0.33026955 0.33522118 0.33450927]
[ 0.33030749 0.33621241 0.3334801 ]
[ 0.33333333 0.33333333 0.33333333]
[ 0.33359229 0.33343927 0.33296844]
[ 0.3351336 0.33240988 0.33245653]
[ 0.33613287 0.33102256 0.33284456]
[ 0.33418585 0.3316118 0.33420235]]
첫번째 항목을 보면, 3개 항목 모두 동일한 확률로 정답으로 예측하고 있다.
두번째 항목을 보면, (0,1,2) 중에서 1이 확률이 높다 (0.334)

6. 계산된 확률 벡터(probs)를 이용하여 정답과의 거리(loss)를 계산한다.
- 먼저 실제 정답을 예측한 확률을 가져온다.
-
- à probs[range(num_examples),y]
- à probs[0, 1, 2, …., 14], [0 0 0 0 0 1 1 1 1 1 2 2 2 2 2]]
- à 이렇게 하면, 0~4까지는 0번째 값을 가져오고, 5~9까지는 1번째, 10~14는 2번째 값을 가져온다.
- Loss 계산
- 위에서 가져온 값을 Log함수의 입력으로 계산하면 loss를 구할 수 있다.
àcorect_logprobs = -np.log(probs[range(num_examples),y])
[[ 0.33333333 0.33333333 0.33333333]
[ 0.33228275 0.33403649 0.33368077]
[ 0.33252159 0.33442546 0.33305295]
[ 0.33454201 0.33331648 0.33214151]
[ 0.33754504 0.3305531 0.33190187]
[ 0.33333333 0.33333333 0.33333333]
[ 0.33394798 0.33267801 0.33337401]
[ 0.33254206 0.33333209 0.33412585]
[ 0.33026955 0.33522118 0.33450927]
[ 0.33030749 0.33621241 0.3334801 ]
[ 0.33333333 0.33333333 0.33333333]
[ 0.33359229 0.33343927 0.33296844]
[ 0.3351336 0.33240988 0.33245653]
[ 0.33613287 0.33102256 0.33284456]
[ 0.33418585 0.3316118 0.33420235]]
[ 1.09861229 1.10176903 1.10105048 1.09499281 1.08605634
1.09861229 1.10058019 1.09861602 1.09296471 1.09001216
1.09861229 1.09970756 1.10124617 1.10007967 1.09600863]
(15, 1)
”2) 항목별 score계산” 의 로직을 수식으로 표현하면 아래와 같다. cross_entropy
여기서 minus를 하는 이유는 자연로그에
0이하의 값이 들어가면 음수가 나오기 때
문에 내부적으로 변환한다.
이 수식의 의미는 log(확률)에서 확률이 1(100%)에 가까워 지면, loss가 0
이 된다는것이다.
즉 잘못된 예측으로 정답을 낮게 예측하면 loss가 커지고, 이후
gradient(기울기)가 커져서 역전파를 통해 파라미터를 조정하게 된다.
예를 들어 -log(0.345) = 1.064라면 e의 1.064승은 0.345이다.
그럼 loss가 0이 나오려면 -log(1) = 0, e의 0승은 1이다
결국 loss를 줄이려면 정답을 예측한 확률이 높아져야 한다. (1에 가깝게)
어떻게 줄이나? à 다음 단계에서 정리..
2) 항목별 score 계산 à 예측에 대한 loss 계산

7. 항목(15개)별로 정답을 예측한 확률의 loss에 대한 평균을 계산한 후,
이 값과 정규화 loss와 합한다.
3) 예측에 대한 loss 계산
계산된 loss는 다음과 같다. (loss : 1.09726151839)계산된 loss는 다음과 같다. (loss : 1.09726151839)
위의 결과는 결국 -log(1/3) 동일한 값이다.
쉽게 말하면 1/3확률로 정답을 예측했다는 의미. à 정확도가 거의 향상되지 못한 상태
이유는 첫번째 학습의 결과이기 떄문에,
이를 최적화하는 단계(역전파를 통한 파라미터 업데이트)를 아직 수행하
지 못했다.
학습이 200회까지 수행되면 좀 더 정확한 확률로 예측할 것이다.

8. 4) Gradient(기울기) 계산 – 1/2
이제 loss를 최소화 하기 위해서 gradient descent를 이용해 보자.
- Loss를 줄이려면 먼저 파라미터(W, b)값을 어떻게 변경해야
- loss가 줄어드는지 알아야 한다.
아래는 loss를 계산하는 수식이고, loss를 계산하기 위한 중간과정으로 정답의 확률을 p에 저장하였다.
그럼 f 내부에서 계산된 scores가 어떻게 변경되어야 loss를 줄일수 있는지 궁금할 것이다. 다른 말로 표현하
면, ∂Li/∂fk를 계산하고자 하는 것이다.
Loss인 Li는 p를 통해서 계산이되고, p는 f함수(여기서는 scores)의 결과에 종속적이다. 최종적으로
gradient는 아래와 같은 간단한 공식으로 도출될 수 있다.
만약 scores의 계산된 확률인 p = [0.2, 0.3, 0.5] (à 정답은 index 1인 0.3)가 있다고 가정하고,
위의 공식에 따라 scores의 gradient를 계산하면 df = [0.2, -0.7, 0.5]가 된다.
이 공식이 의미하는게 무엇일까?
à다시 loss를 계산하는 수식을 보면, “Li = -log(p)” 이고 p가 높을수록 loss는 줄어든다.
à만약 우리가 loss를 줄이려고, 잘못된 정답인 scores의 inde 0 또는 2번째 값을 증가시키면 어떻게 될까?
àP값이 [0.3, 0.1, 0.6]처럼 오히려 정답의 확률이 더 떨어지게 되어, loss가 증가한다.
à그래서 정답의 scores(index 1)를 높여야 한다.
à그럼 정답의 scores를 높이려면 loss가 줄어들도록 f(scores)를 조정해야한다. (즉 기울기가 음수)
à 위 공식은 “f함수가 Loss에 minus(negative)영향을 주도록 한다”는 의미다.
à즉 df = [0.2, -0.7, 0.5] è f(scores)의 index 1에 해당하는 값을 1 증가시키면 à loss에 -0.7만큼 줄어든
다.
정답(100%)과 예측한 확률(30%)의 차이를 계산하면, f가 Li에 미치는 영향
(기울기)를 알 수 있다.

9. 4) Gradient(기울기) 계산 – backup
어떻게 위와 같은 공식이 나왔는지에 대한 설명

10. 4) Gradient(기울기) 계산 – 2/2
dscores = probs
dscores[range(num_examples),y] -= 1
[[-0.04444444 0.02222222 0.02222222]
[-0.04451448 0.0222691 0.02224538]
[-0.04449856 0.02229503 0.02220353]
[-0.04436387 0.0222211 0.02214277]
[-0.04416366 0.02203687 0.02212679]
[ 0.02222222 -0.04444444 0.02222222]
[ 0.0222632 -0.04448813 0.02222493]
[ 0.02216947 -0.04444453 0.02227506]
[ 0.02201797 -0.04431859 0.02230062]
[ 0.0220205 -0.04425251 0.02223201]
[ 0.02222222 0.02222222 -0.04444444]
[ 0.02223949 0.02222928 -0.04446877]
[ 0.02234224 0.02216066 -0.0445029 ]
[ 0.02240886 0.02206817 -0.04447703]
[ 0.02227906 0.02210745 -0.04438651]]
dscores
[[-0.66666667 0.33333333 0.33333333]
[-0.66629358 0.33431919 0.33197439]
[-0.66604902 0.33558568 0.33046334]
[-0.66679333 0.33454222 0.33225111]
[-0.66817665 0.32953226 0.33864438]
[ 0.33333333 -0.66666667 0.33333333]
[ 0.33303264 -0.66778284 0.3347502 ]
[ 0.3332074 -0.66802141 0.33481401]
[ 0.33440814 -0.66417015 0.32976201]
[ 0.33466927 -0.66213759 0.32746832]
[ 0.33333333 0.33333333 -0.66666667]
[ 0.33348317 0.33421333 -0.6676965 ]
[ 0.33274968 0.33241886 -0.66516854]
[ 0.3322957 0.32994002 -0.66223571]
[ 0.33302089 0.33049026 -0.66351115]]
dscores
위 공식으로 f(scores)의 어떤 index 값을 증가시켜야, loss가 줄어드는지 알 수 있게 되었다.
dscores /= num_examples # gradient
(15, 3)
정답의 확률에 -1을 한 결과.
Dscores를 전체 개수
(num_exmaples, 15)로 나
누어서 전체에서 미치는 영
향으로 조정해 준다. .

11. 5) Parameter 조정 (W, b) – 1/2
Gradient가 적용된 scores(dscores에 저장됨)를 통해서, W와 b로 역전파 해보자.
공식(scores = np.dot(X, W) + b)라는 공식이 이미 있으므로,
- 역전파된 W(dW) = np.dot(X.T, dscores) 로 계산하고, (2,3) = (2, 15) * (15,3)
- 역전파된 b(db) = np.sum(dscores, axis=0, keepdims=True)
(2, 3)
[[-0.00911365 0.00989886 0.00200746]
[-0.00616948 0.00392478 0.00670659]]
[[ 0. 0. 0.]]
W
b
[[-0.01442236 -0.08168074 0.0961059 ]
[ 0.08424138 -0.08170848 -0.00252844]]
[[ 2.00204394e-04 -1.16085086e-04 -8.41193073e-05]]
dW
db(1, 3)
[[-0.04444444 0.02222222 0.02222222]
[-0.04451448 0.0222691 0.02224538]
[-0.04449856 0.02229503 0.02220353]
[-0.04436387 0.0222211 0.02214277]
[-0.04416366 0.02203687 0.02212679]
[ 0.02222222 -0.04444444 0.02222222]
[ 0.0222632 -0.04448813 0.02222493]
[ 0.02216947 -0.04444453 0.02227506]
[ 0.02201797 -0.04431859 0.02230062]
[ 0.0220205 -0.04425251 0.02223201]
[ 0.02222222 0.02222222 -0.04444444]
[ 0.02223949 0.02222928 -0.04446877]
[ 0.02234224 0.02216066 -0.0445029 ]
[ 0.02240886 0.02206817 -0.04447703]
[ 0.02227906 0.02210745 -0.04438651]]
(15, 3)
Scores = W * X è 𝑋"
를 곱해준다.
Scores * 𝑋"
= W
https://ko.wikipedia.org/wiki/%ED%96
%89%EB%A0%AC
Regularization을 위한 수식 추가

12. 5) Parameter 조정 (W, b) – 2/2
지금까지 어떤 파라미터가 loss에 어떤 영향을 주는지 알 수 있는 gradient를 계산하였다.
이제 loss를 줄일 수 있도록 minus(negative)방향으로 파라미터를 업데이트 해 보자.
(2, 3)
[[-0.00911365 0.00989886 0.00200746]
[-0.00616948 0.00392478 0.00670659]]
[[ 0. 0. 0.]]
W
b
[[-0.01442236 -0.08168074 0.0961059 ]
[ 0.08424138 -0.08170848 -0.00252844]]
[[ 2.00204394e-04 -1.16085086e-04 -8.41193073e-05]]
dW
db(1, 3)
[[ 0.00530871 0.0915796 -0.09409844]
[-0.09041086 0.08563326 0.00923503]]
[[ -2.00204394e-04 1.16085086e-04 8.41193073e-05]]
W
b
[[ 0.30340715 0.34121343 0.35537942]
[ 0.19492407 0.62935153 0.1757244 ]
[ 0.71597869 0.1856451 0.09837621]
[ 0.90652466 0.02325688 0.07021846]
[ 0.60784668 0.00312771 0.38902561]
[ 0.30340715 0.34121343 0.35537942]
[ 0.17694003 0.25262399 0.57043598]
[ 0.04740059 0.57891371 0.37368569]
[ 0.01159157 0.94431966 0.04408876]
[ 0.25428663 0.73547774 0.01023563]
[ 0.30340715 0.34121343 0.35537942]
[ 0.55288955 0.21052905 0.2365814 ]
[ 0.52296824 0.03916278 0.43786898]
[ 0.09059707 0.02332037 0.88608256]
[ 0.00808054 0.35200296 0.63991651]]
[[ 0.33333333 0.33333333 0.33333333]
[ 0.33228275 0.33403649 0.33368077]
[ 0.33252159 0.33442546 0.33305295]
[ 0.33454201 0.33331648 0.33214151]
[ 0.33754504 0.3305531 0.33190187]
[ 0.33333333 0.33333333 0.33333333]
[ 0.33394798 0.33267801 0.33337401]
[ 0.33254206 0.33333209 0.33412585]
[ 0.33026955 0.33522118 0.33450927]
[ 0.33030749 0.33621241 0.3334801 ]
[ 0.33333333 0.33333333 0.33333333]
[ 0.33359229 0.33343927 0.33296844]
[ 0.3351336 0.33240988 0.33245653]
[ 0.33613287 0.33102256 0.33284456]
[ 0.33418585 0.3316118 0.33420235]]
(15,3)
200회 학습
5개 정답
33% 정확도
9개 정답
60% 정확도

13. 6) 최종 분류결과 시각화
테스트로 생성된 데이터에 맞추어서 최대한 분류를 하기는 했지만,
그래도 정확도는 60%로 높지 않다.
그럼 이를 해결하기 위해서 Neural Network를 적용해 보자.

14. Neural Network
Back Propagation 이해

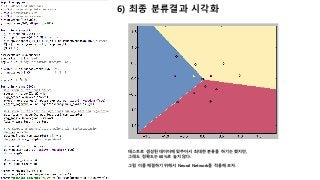
15. 1) Data set 준비
이전 과정과 동일하므로, 자세한 설명은 생략하고 생성된 데이터만 정리한다.
[[ 0. 0. ]
[ 0.18857724 0.1641299 ]
[ 0.42357607 -0.26567519]
[-0.06458412 -0.74721409]
[-0.71361665 -0.70053642]
[-0. -0. ]
[-0.23857252 0.07472049]
[-0.21048641 0.45353663]
[ 0.53144134 0.5292165 ]
[ 0.98338959 -0.18150734]
[ 0. -0. ]
[ 0.10836615 -0.22529265]
[-0.33969385 -0.36688975]
[-0.74720028 0.06474361]
[-0.49769084 0.8673545 ]]
X
(15,2)
[[ 9.59124370e-03 -1.99526771e-02 -2.41337159e-02 2.45046904e-02
-1.19709499e-02 3.06484488e-03 -1.16120293e-02 3.18609479e-03
-3.54761775e-03 -1.29747531e-02 -6.70712304e-03 8.14215039e-04
………
1.44553626e-02 3.65345303e-03 -9.18739281e-03 4.01347715e-03
6.24115177e-03 1.36143555e-03 -1.00980011e-02 -3.56963089e-03]
[ -8.79587147e-03 -9.55833368e-03 -2.36122907e-02 -2.10972292e-03
-1.81231810e-03 -5.39162676e-03 -2.77592161e-03 -1.25245349e-02
……..
8.13563661e-03 -4.31994497e-03 -1.38893369e-02 -1.92325604e-02
-2.61766602e-03 -1.17921701e-02 2.02177760e-04 8.91664578e-03
-1.60389098e-02 -7.08560776e-03 -5.55375335e-03 -5.43286945e-04]]
[[ 0. 0. 0. 0. 0. 0. 0. 0. 0. 0. 0. 0. 0. 0. 0. 0. 0. 0.
0. 0. 0. 0. 0. 0. 0. 0. 0. 0. 0. 0. 0. 0. 0. 0. 0. 0.
0. 0. 0. 0. 0. 0. 0. 0. 0. 0. 0. 0. 0. 0. 0. 0. 0. 0.
0. 0. 0. 0. 0. 0. 0. 0. 0. 0. 0. 0. 0. 0. 0. 0. 0. 0.
0. 0. 0. 0. 0. 0. 0. 0. 0. 0. 0. 0. 0. 0. 0. 0. 0. 0.
0. 0. 0. 0. 0. 0. 0. 0. 0. 0.]]
W
(2, 100)
b
(1, 100)
[[ -2.05698506e-03 2.13984123e-02 4.53365951e-03]
[ 8.45085108e-03 8.21498954e-03 1.63043624e-02]
[ 5.75243675e-03 -3.94968527e-03 -1.54880022e-02]
……..
[ 1.52845394e-02 -2.48438130e-02 6.92445923e-03]
[ 1.40816279e-02 -8.57505500e-03 -9.75438424e-03]
[ 1.18932602e-02 -5.47826939e-03 -1.90667634e-02]]
[[ 0. 0. 0.]]
W2
(100, 3)
b2
(1, 3)
y
(15,1)
[0 0 0 0 0 1 1 1 1 1 2 2 2 2 2]
5

16. 2) Score 계산
이전 과정과 달라진 것은, Layer가 2개로 증가하면서 사용한 파라미터도 W2, b2가 추가되었다.
[0 0 0 0 0 1 1 1 1 1 2 2 2 2 2]
X
(15, 2)
W
(2, 100) (2, 100) (15, 100)
b
Hidde_layer
(15, 100)
Hidde_layer
(100, 3)
W2 b2
(1, 3)
scores
(15, 3)
5

17. 3) Gradient(기울기) 계산
최종적으로 계산된 scores를 이용하여 gradient를 계산하는 방식은 동일하다.
[[-0.04444444 0.02222222 0.02222222]
[-0.04444487 0.02222214 0.02222273]
[-0.0444473 0.022223 0.0222243 ]
[-0.04443276 0.02221423 0.02221853]
[-0.04442131 0.02220272 0.02221859]
[ 0.02222222 -0.04444444 0.02222222]
[ 0.0222268 -0.04444305 0.02221625]
[ 0.02222814 -0.04443548 0.02220734]
[ 0.02222161 -0.04444399 0.02222238]
[ 0.02221217 -0.0444425 0.02223033]
[ 0.02222222 0.02222222 -0.04444444]
[ 0.02222299 0.02222158 -0.04444456]
[ 0.02223368 0.02221246 -0.04444614]
[ 0.02223572 0.0222224 -0.04445812]
[ 0.02223421 0.02224007 -0.04447428]]
dscores
(15, 3)
5

18. 4) Gradient를 Parameter로 역전파 하기
이전과 다른 점은 기존에는 score à dW à W로 변경하였으나,
NN에서는 layer가 여러개 있으므로, 뒤에서부터 파라미터를 역전파 한다.
dW2 = np.dot(hidden_layer.T, dscores)
db2 = np.sum(dscores, axis=0, keepdims=True)
dhidden = np.dot(dscores, W2.T) # next backprop into hidden layer
dhidden[hidden_layer <= 0] = 0 # backprop the ReLU non-linearity
dW = np.dot(X.T, dhidden)
db = np.sum(dhidden, axis=0, keepdims=True)
dW2 += reg * W2
dW += reg * W
dscoresdW2
db2
dhiddendW
db
dhidden
Relu
W += -step_size * dW
b += -step_size * db
W2 += -step_size * dW2
b2 += -step_size * db2
5

19. 5) 최종 분류결과 시각화
Data set을 15개로 줄여서 태스트 한 결과, 정확도가 softmax(60%) à NN(87%)로 높아졌다.
원래 예제인
training accuracy: 0.87
5