More Related Content
PPTX
PDF
魁!!広島ベイズ塾(2015.7.26.)「正規分布(+対数正規分布)について」 PDF
計算で明らかにするタンパク質の出会いとネットワーク(FIT2016 助教が吼えるセッション) PDF
PPTX
StanとRでベイズ統計モデリング読書会(Osaka.stan) 第6章 PPTX
PPTX
PDF
2021年度秋学期 統計学 第11回 分布の「型」を考える ー 確率分布モデルと正規分布(2021. 12. 7) Similar to Bgnd kobe.r5
PPTX
PPTX
Introduction to Statistical Estimation (統計的推定入門) PDF
PDF
2022年度春学期 統計学 第11回 分布の「型」を考えるー確率分布モデルと正規分布 PPT
PPTX
PDF
PDF
PDF
PPTX
PPTX
PDF
2022年度秋学期 統計学 第11回 分布の「型」を考える - 確率分布モデルと正規分布 (2022. 12. 6) PPTX
PDF
2013年度秋学期 統計学 第14回「分布についての仮説を検証する ― 仮説検定」 PDF
2020年度秋学期 統計学 第11回 分布の「型」を考えるー確率分布モデルと正規分布 (2020. 12. 8) PPT
PPTX
Exponential distribution (指数分布) PDF
PPTX
Bernoulli distribution and multinomial distribution (ベルヌーイ分布と多項分布) PDF
2016年度秋学期 統計学 第11回 分布の「型」を考える-確率分布モデルと正規分布 (2016. 12. 5) More from florets1
PDF
PPT
PPT
Osaka prml reading_3.2-3.3.1 PPT
PPT
PPT
PPT
Osaka prml reading_2.3.1-2 PPT
PPT
PPT
Bgnd kobe.r5
- 1.
- 2.
- 3.
- 4.
- 5.
- 6.
- 7.
- 8.
- 9.
- 10.
- 11.
- 12.
- 13.
- 14.
- 15.
15
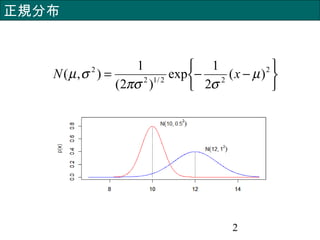
連続確率変数 x の場合は正規分布
∫=1)( dxxp制約条件
求め方
のもとで
を最大化する。
∫ = µdxxxp )(
∫ =− 22
)()( σµ dxxpx
dxxpxpxH )(log)(][ ∫−=
エントロピーが最大となる確率分布(連続)
- 16.
- 17.








![11
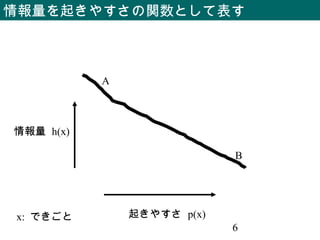
エントロピー 情報量の平均
)(log)(][ xpxpxH
x
∑−=
dxxpxpxH )(log)(][ ∫−=
離散確率変数 x の場合
連続確率変数 x の場合](https://image.slidesharecdn.com/bgndkobe-140613195004-phpapp02/85/Bgnd-kobe-r5-11-320.jpg)
![12
エントロピーの性質
bitxH 2
64
1
log
64
4
16
1
log
16
1
8
1
log
8
1
4
1
log
4
1
2
1
log
2
1
][ 22222 =−−−−−=
x の 8 個の状態それぞれの確率が
{1/2,1/4,1/8,1/16,1/64,1/64,1/64,1/64} の場合のエントロピー
bitxH 3
8
1
log
8
1
8][ 2 =×−=
x が 8 個の状態を等確率で取る場合のエントロピー](https://image.slidesharecdn.com/bgndkobe-140613195004-phpapp02/85/Bgnd-kobe-r5-12-320.jpg)

![14
エントロピーが最大となる確率分布(離散)
離散確率変数 x の場合は一様分布
)(log)(][ xpxpxH
x
∑−=
1)( =∑x
xp制約条件
求め方
のもとで
を最大化する。](https://image.slidesharecdn.com/bgndkobe-140613195004-phpapp02/85/Bgnd-kobe-r5-14-320.jpg)
![15
連続確率変数 x の場合は正規分布
∫ =1)( dxxp制約条件
求め方
のもとで
を最大化する。
∫ = µdxxxp )(
∫ =− 22
)()( σµ dxxpx
dxxpxpxH )(log)(][ ∫−=
エントロピーが最大となる確率分布(連続)](https://image.slidesharecdn.com/bgndkobe-140613195004-phpapp02/85/Bgnd-kobe-r5-15-320.jpg)

