This document contains an individual assignment for an Algebra course at Universiti Tun Hussein Onn Malaysia. The assignment includes two questions. Question 1 has parts (a) and (b) that involve solving equations using completing the squares and the quadratic formula. Question 2 asks the student to show that -1 is a root of the given equation and then factorize it completely. It also asks the student to calculate the composition of some given functions.

1. UNIVERSITI TUN HUSSEIN ONN MALAYSIA
86400 PARIT RAJA, BATU PAHAT
TUGASAN INDIVIDU
PROGRAM SARJANA MUDA PENDIDIKAN ( SEKOLAH RENDAH )
ALGEBRA ( BBR 23703 )
NAMA : NOR KHARI IZARDI BIN ISMAIL
NO. K.PENGENALAN : 820101 – 06 – 6353
NO. MATRIK : DB 100058
PPG : SAINS SEKSYEN 3
NAMA PENSYARAH : DR. MUHD. SAIFULLAH BIN RUSIMAN

2. BBR 23703
ALGEBRA
INDIVIDUAL ASSIGNMENT NO. 1
Question 1 [5%]
(a) Solve 3x² + 2x² - 5 = 0 by
(i) completing the squares
Solution
3x² + 2² = 0
3x² + 2x = 5
3x² + 2x= 5
3 3 3
x² + 2x = 5
3 3
x² + 2x + 3 ² = 5 + 3 ²
3 2 3 2
x² + 2x + 2 ² = 5 + 2 ²
3 6 3 6
x² + 2x + 1 ² = 5 + 1 ²
3 3 3 3

3. x + 1 ² = 5 + 1
3 3 9
x + 1 ² = 16
3 9
x + 1 = ⁺₋ 16
3 9
x + 1 = ⁺₋ 4
3 3
x + 1 = 4
3 3
x = 4 - 1 atau x = - 4 - 1
3 3 3 3
x = 3 x = - 5
2 3
X = 1

4. ii) Quadratic formula
3x2
+ 2x – 5 = 0
a = 3 b = 2 c = -5
x = -b ± b2
– 4ac
2a
x = - (2) ± (2)2
– 4 (3) (-5)
2 (3)
x = -2 ± 4 – 12 ( -5)
6
x = -2 ± 64
6
x = -2 ± 8
6
x = -2 + 8 atau x = - 2 - 8
6 6
x = 1 atau x = - 1.667

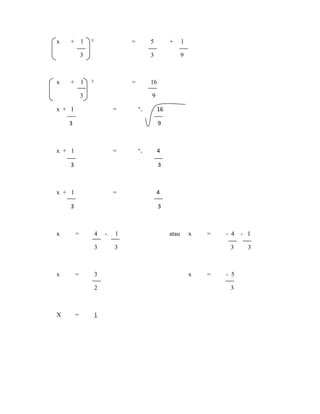
5. Question 2[ 5%]
b. Show that -1 is the root of x3
–2x2
–x + 2
Hence, factorize completely.
Solution:
x3
–2x2
– x + 2
= [ –1 ]3
– 2 [ –1 ]2
– [ –1 ] + 2
= 0
Showed
x3
– 2x2
– x + 2
= x [ x2
– 2x – 1 ] + 2

6. BBR 23703
ALGEBRA
INDIVIDUAL ASSIGNMENT NO. 2
Question 1 [6%]
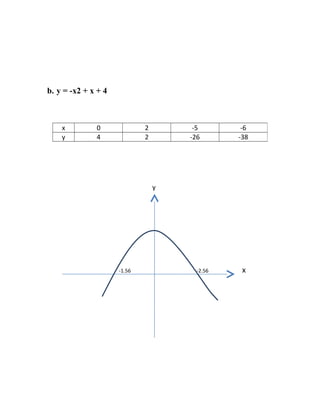
Sketch the graph and determine the domain and range.
a. y = 2x + 7
Solution:
y = 2x + 7
y
x
x 20 40 0 10
y 47 87 7 27

7. b. y = -x2 + x + 4
y
-1.56 -2.56 x
x 0 2 -5 -6
y 4 2 -26 -38

8. c. y =
y
x
x 2 5 10
y 1 0.25 0.02
____1____
[ x-3]2

9. Question 2 [4%]
Given f ( = + 4 , g ( + and h ( = 2
Calculate
a) f o g
f g ( = f
= f
= __3_ + 4
= _9_ + 4
²

10. b) f o g o h = fg
= fg
= _9_ + 4
²
= _9_ + 4
²