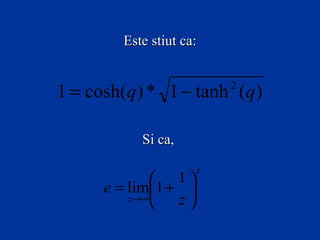Documentul abordează eleganța profesională în exprimarea ecuațiilor matematice, subliniind faptul că notările simple pot fi transformate în forme mai complexe și științifice. Autorul exemplifică cum suma 1 + 1 poate fi reprezentată prin diversificate expresii matematice elaborate, care sunt mai sofisticate și estetice. Scopul este de a arăta că inginerii pot, de asemenea, să complice lucrurile într-un mod creativ, similar cu avocații și economiștii.

1. Eleganta Profesionala...
Oricare inginer intelege notatia matematica conform
careia suma a doua numere reale,
spre exemplu
1+1 = 2
poate fi scrisa intr-o maniera foarte simpla.
Fara indoiala, putem spune ca este o lipsa totala de
stil.

2. Din primii ani de matematica stim ca,
1 = ln(e)
Si de asemenea ca,
1 = sin ( p ) + cos ( p )
2 2
In plus, toti stim ca,
∞ n
1 
2 =∑  
n=  2 
0

3. Pentru asta expresia,
1+1 = 2
Poate fi rescrisa intr-o forma mai eleganta asa :
∞ n
1
ln ( e ) + sin ( p ) + cos ( p ) = ∑  
2 2
n =0  2 
Care, asa cum usor se poate observa, este mult mai
stiintifica.

4. Este stiut ca:
1 = cosh(q ) * 1 − tanh (q )
2
Si ca,
z
 1
e = lim1 + 
z →∞
 z

5. de unde rezulta,
∞ n
1
ln ( e ) + sin ( p ) + cos ( p ) = ∑  
2 2
n =0  2 
Care poate fi scrisa in urmatoarea forma, mai clara si
mai transparenta,
  1 2  ∞
cosh(q ) * 1 − tanh 2 (q)
ln lim1 +   + sin 2 ( p ) + cos 2 ( p ) = ∑
 z →∞ z  2n
  n =0

6. Tinand cont ca,
0!= 1
Si ca matricea inversa a matricii transpuse este aceeasi
cu matricea transpusa a matricii inverse (conform
ipotezei spatiului unidimensional), obtinem
urmatoarea simplificare (datorita notarii vectoriale) :
(X ) − (X )
T −1 −1 T
=0

7. Daca unificam expresiile simplificate,
0!= 1
si
(X ) − (X )
T −1 −1 T
=0
Se obtine,

( ) − (X )
 X

T −1 −1 T 
!= 1


8. Aplicand simplificarile descrise anterior, rezulta ca din
ecuatia:
  1 2  ∞
cosh(q ) * 1 − tanh 2 (q )
ln lim1 +   + sin ( p ) + cos ( p ) = ∑
2 2
 z →∞ z   2n
  n =0
Obtinem in final intr-o forma foarte eleganta, legibila,
succinta si de inteles pentru toti, ecuatia:
  T
( ) − (X ) 
2
−1 −1 T  1  + sin 2 ( p ) + cos 2 ( p ) = ∑
∞
cosh(q ) * 1 − tanh 2 (q )
ln lim  X !+ 
 z →∞   z  2n
  n =0
(care, trebuie sa admitem, este mult mai profesionala decat
vulgara si taraneasca expresie a ecuatiei originale)
1 +1 = 2

9. Aceasta prezentare a fost facuta pentru prietenii avocati ( si
eventual economisti ) ca sa stie ca si noi , inginerii putem
complica lucrurile la nesfarsit.
Poti de asemenea sa il trimiti prietenilor ingineri care stiu sa
aprecieze umilul spirit ingineresc care ii anima.