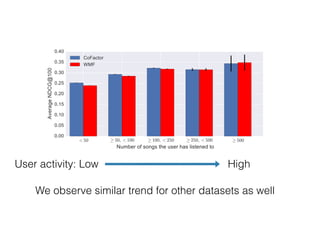
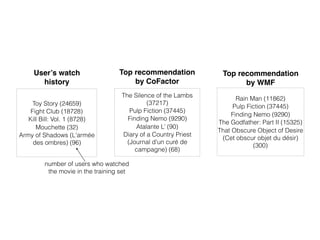
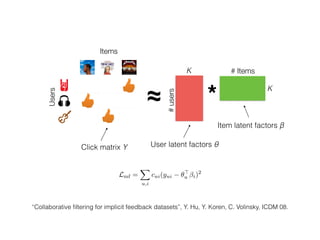
The document presents the CoFactor model, which jointly factorizes the user-item click matrix and item-item co-occurrence matrix to improve recommender system performance. CoFactor is motivated by word embedding models like word2vec that learn embeddings from word co-occurrence. It outperforms weighted matrix factorization on several datasets based on quantitative and qualitative evaluations. The authors analyze the model fits and show its benefits from accounting for item co-occurrence patterns in user data.







![Levy & Goldberg show that skip-gram
word2vec is implicitly factorizing (some
variation of) the pointwise mutual
information (PMI) matrix
“Neural Word Embedding as Implicit Matrix Factorization”, Levy & Goldberg, NIPS 14.
ct of
held-
dings
ories
ords.
earn
erred
the
used
item
tions
that
eable
ather
s for
intly
locks
item
how
Mikolov et al. [13] for more details).
Levy and Goldberg [10] show that word2vec with a neg-
ative sampling value of k can be interpreted as implicitly
factorizing the pointwise mutual information (PMI) matrix
shifted by log k. PMI between a word i and its context word
j is defined as:
PMI(i, j) = log
P(i, j)
P(i)P(j)
Empirically, it is estimated as:
PMI(i, j) = log
#(i, j) · D
#(i) · #(j)
.
Here #(i, j) is the number of times word j appears in the
context of word i. D is the total number of word-context
pairs. #(i) =
P
j #(i, j) and #(j) =
P
i #(i, j).
After making the connection between word2vec and matrix
factorization, Levy and Goldberg [10] further proposed to
perform word embedding by spectral dimensionality reduc-
tion (e.g., singular value decomposition) on shifted positive
PMI (SPPMI) matrix:
SPPMI(i, j) = max max{PMI(i, j), 0} log k, 0
This is attractive since it does not require learning rate and
current
word/item
context
word/item
Co-occurrence matrix
• PMI(“Pluto”, “planet”) > PMI(“Pluto”, “RecSys”)](https://image.slidesharecdn.com/cofactor-161005194202/85/Factorization-Meets-the-Item-Embedding-Regularizing-Matrix-Factorization-with-Item-Co-occurrence-9-320.jpg)




![Quantitative results
ArXiv ML-20M TasteProfile
WMF CoFactor WMF CoFactor WMF CoFactor
Recall@20 0.063 0.067 0.133 0.145 0.198 0.208
Recall@50 0.108 0.110 0.165 0.177 0.286 0.300
NDCG@100 0.076 0.079 0.160 0.172 0.257 0.268
MAP@100 0.019 0.021 0.047 0.055 0.103 0.111
ble 2: Comparison between the widely-used weighted matrix factorization (WMF) model [8] and our CoFactor mode
Factor significantly outperforms WMF on all the datasets across all metrics. The improvement is most pronounced on th
ovie watching (ML-20M) and music listening (TasteProfile) datasets.
rameter indicates that the model benefits from account-
g for co-occurrence patterns in the observed user behavior
ta. We also grid search for the negative sampling values
2 {1, 2, 5, 10, 50} which e↵ectively modulate how much to
ft the empirically estimated PMI matrix.
4 Analyzing the CoFactor model fits
Table 2 summarizes the quantitative results. Each metric
averaged across all users in the test set. As we can see,
• We get better results by simply re-using the data
• Item co-occurrence is in principle available to
MF model, but MF model (bi-linear) has limited
modeling capacity to make use of it](https://image.slidesharecdn.com/cofactor-161005194202/85/Factorization-Meets-the-Item-Embedding-Regularizing-Matrix-Factorization-with-Item-Co-occurrence-14-320.jpg)