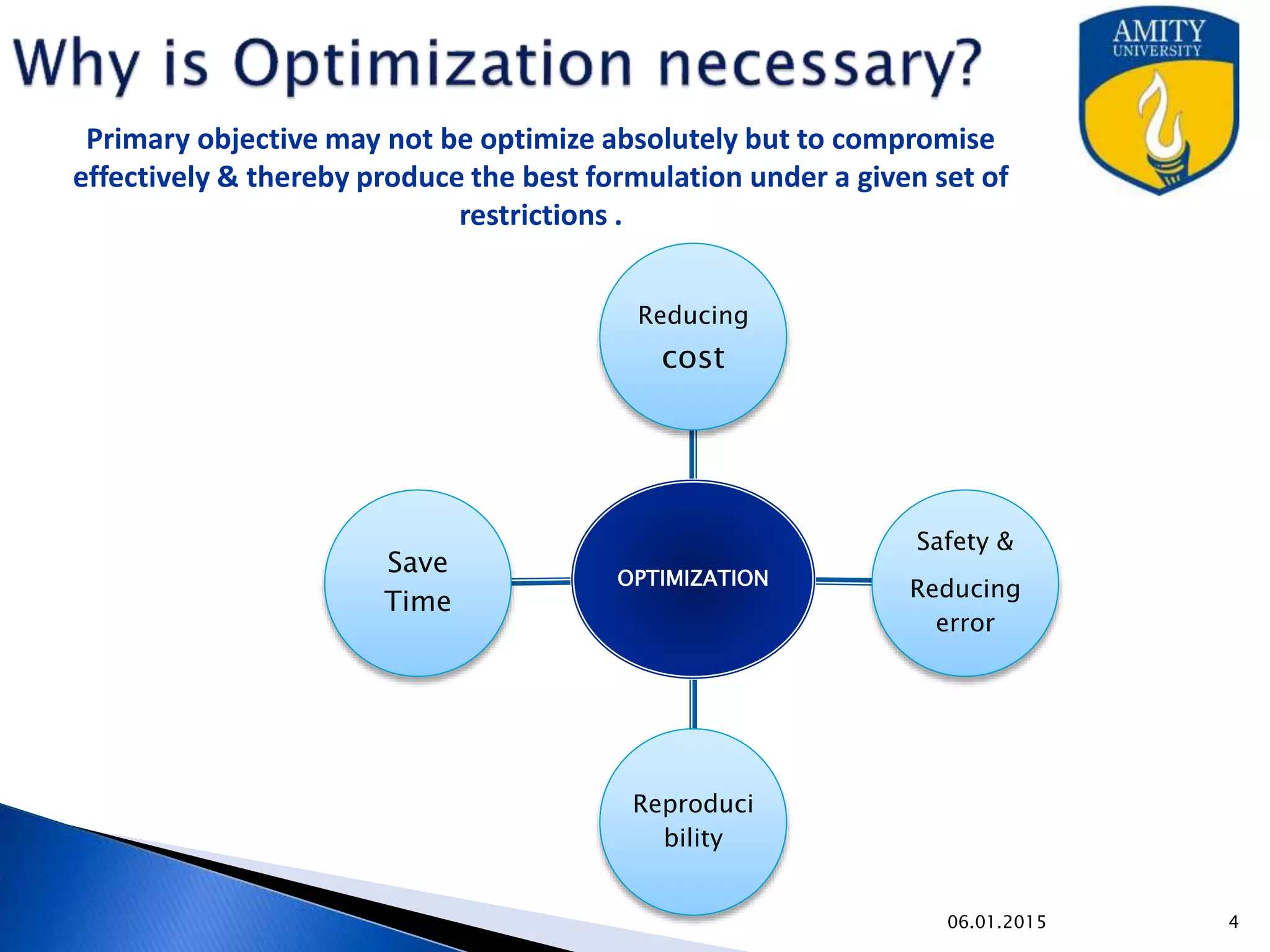
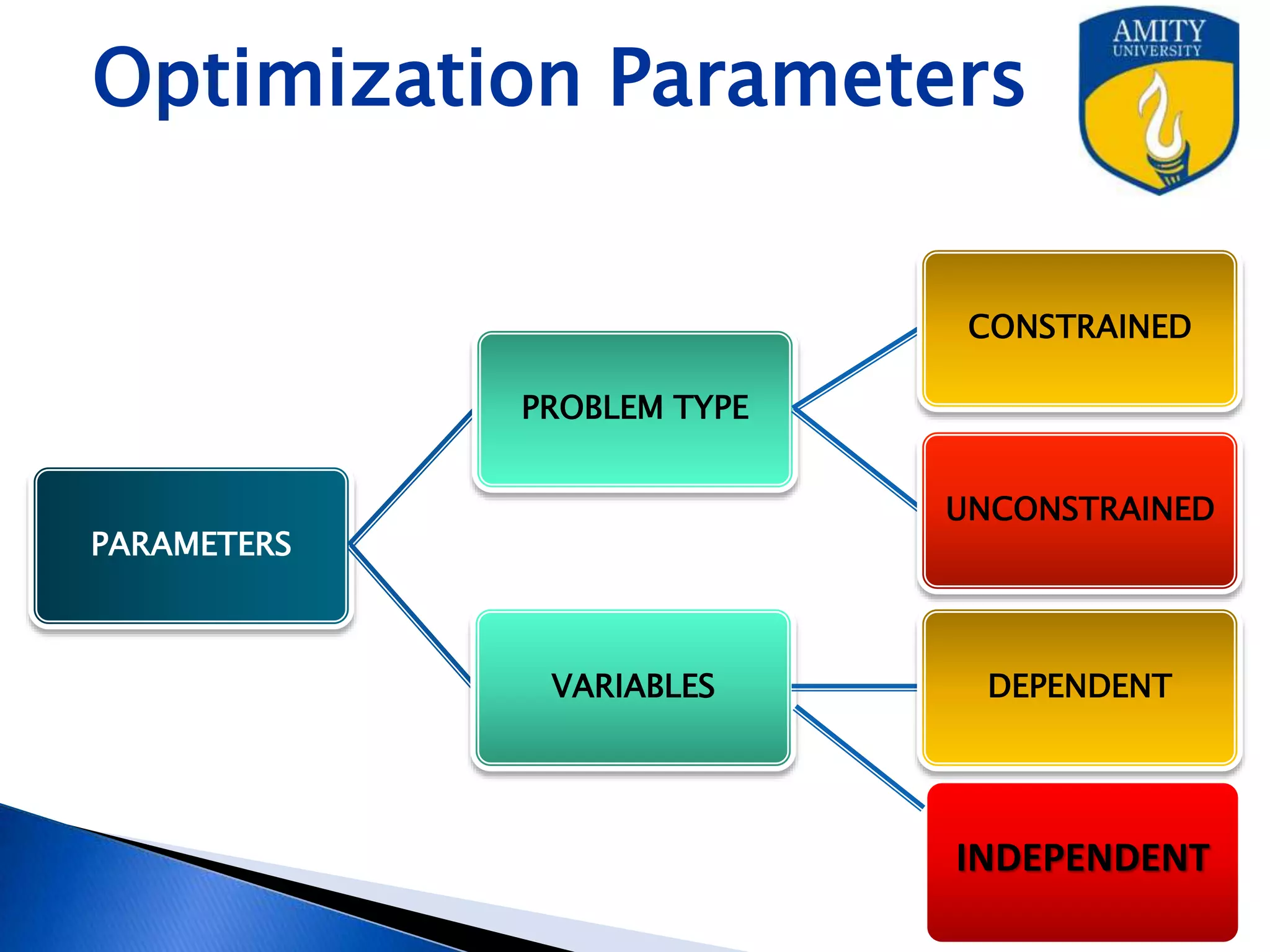
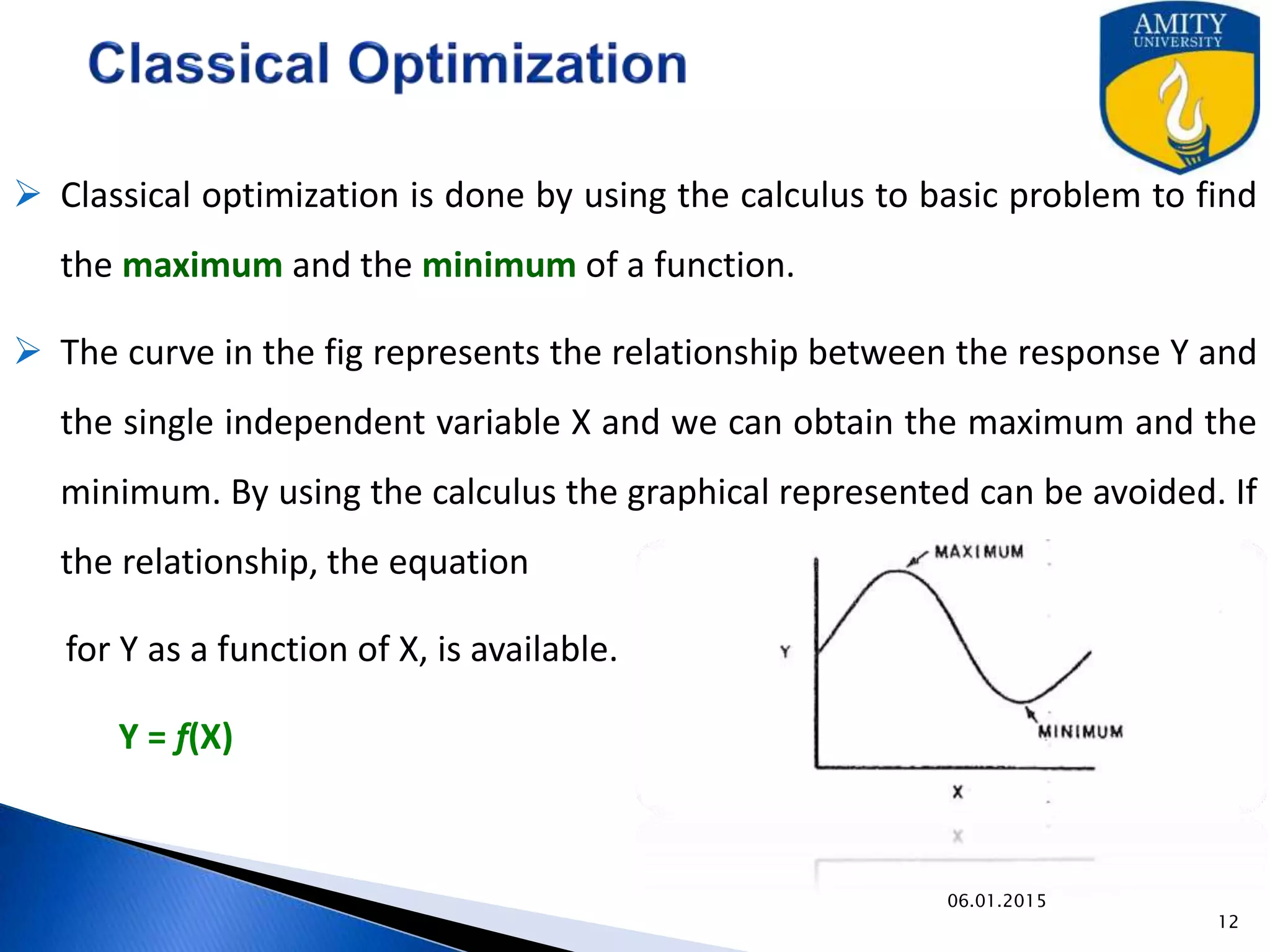
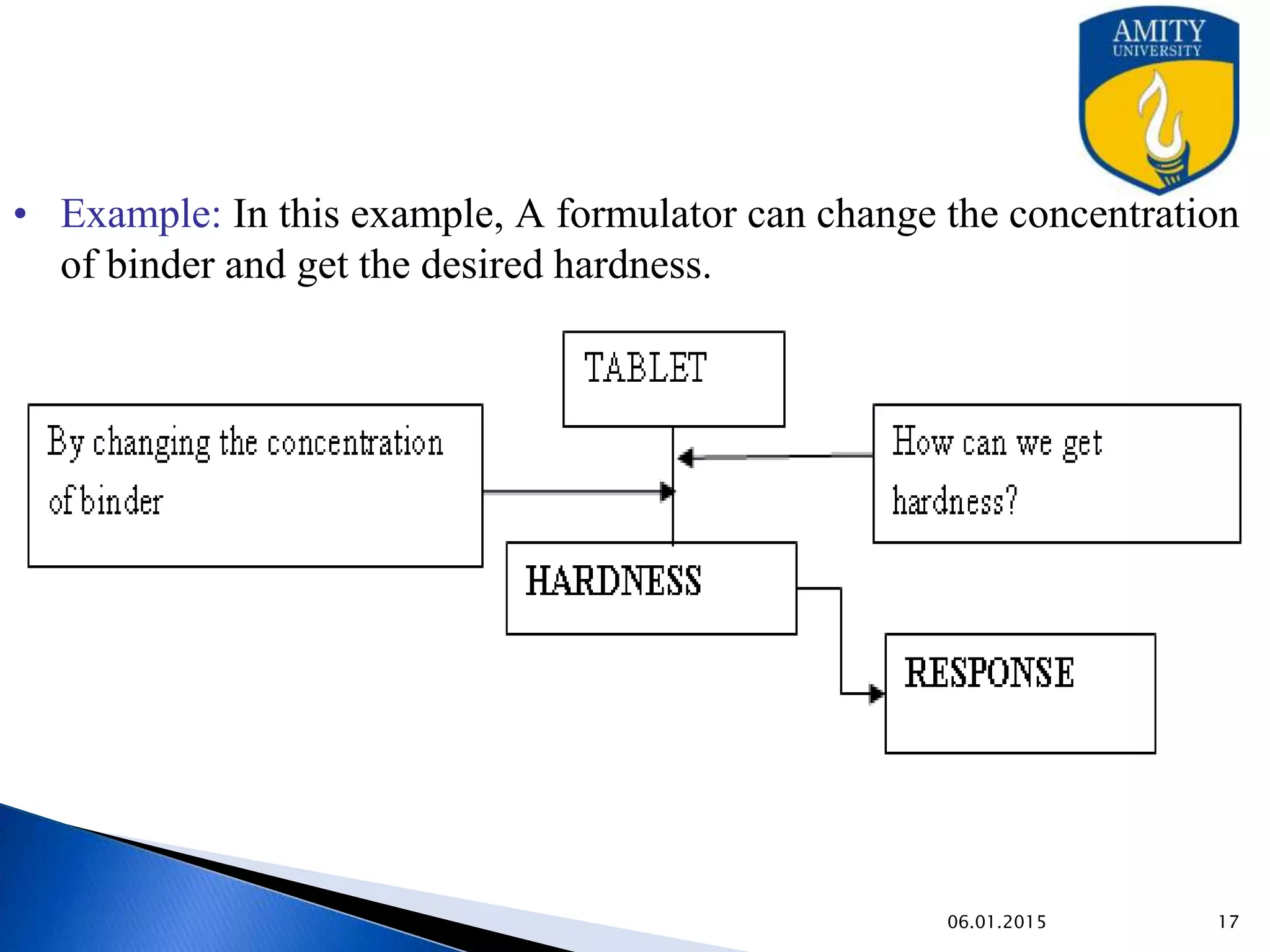
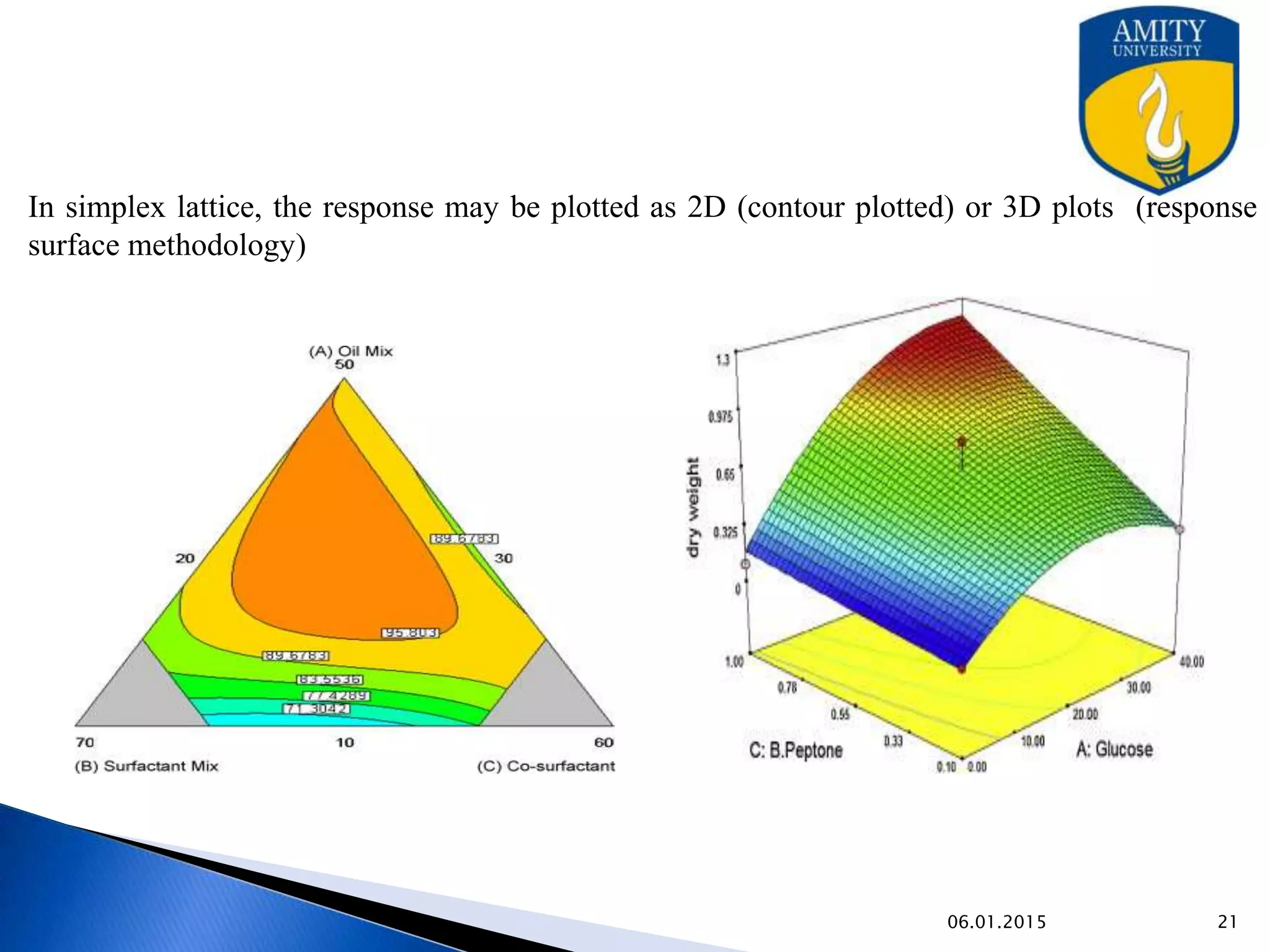
Optimization techniques are used in pharmaceutical formulation and processing to improve quality while reducing costs. Various methods like evolutionary operation, simplex lattice, and Lagrangian methods can be used to optimize multiple variables. Optimization helps identify the ideal levels of factors like concentration, temperature, and mixing time to achieve the desired response. The techniques allow for more efficient development and large-scale production of drugs.

1. Optimization Techniques
In Pharmaceutical
Formulation &
Processing
Anirban Saha,
Navneet Kumar Giri
M.Pharm (Pharmaceutics)
Year- 2nd , Semester- 3
Amity University, Noida
AMITY INSTITUTE
OF PHARMACY

2. Outline
 Introduction
 Why Necessary
 Terms Used
 Advantages
 Optimization parameters
 Problem type
 Variables
 Applied optimisation methods
 Other Applications
 Factorial Design
 Conclusion
9/27/2015

3. Introduction
The term Optimize is defined as to make perfect , effective , or as functional
as possible.
It is the process of finding the best way of using the existing resources while
taking in to the account of all the factors that influences decisions in any
experiment
 Traditionally, optimization in pharmaceuticals refer to changing one variable
at a time, so to obtain solution of a problematic formulation.
Modern pharmaceutical optimization involves systematic design of
experiments (DoE) to improve formulation irregularities.
In the other word we can say that –quantitate a formulation that has been
qualitatively determined . It’s not a screening technique.
9/27/2015

4. Why is Optimization necessary?
9/27/2015
OPTIMIZATION
Reducing
cost
Safety &
Reducing
error
Reproducib
ility
Save
Time
Primary objective may not be optimize absolutely but to compromise
effectively & thereby produce the best formulation under a given set of
restrictions .

5. Terms Used
o FACTOR: It is an assigned variable such as concentration , Temperature
etc..,
• Quantitative: Numerical factor assigned to it
Ex- Concentration- 1%, 2%,3% etc.
• Qualitative: Which are not numerical
Ex- Polymer grade, humidity condition etc.
o LEVELS: Levels of a factor are the values or designations assigned to
the factor.
o RESPONSE: It is an outcome of the experiment.
• It is the effect to evaluate.
Ex- Disintegration time.
9/27/2015

6. Terms Used
oEFFECT: It is the change in response caused by varying the
levels
 It gives the relationship between various factors & levels.
oINTERACTION: It gives the overall effect of two or more
variables
Ex- Combined effect of lubricant and glidant on hardness of
the tablet
9/27/2015
FACTOR LEVELS
Temperature 300 , 500
Concentration 1%, 2%

7. Advantages
o Yield the “Best Solution” within the domain of study.
o Require fewer experiments to achieve an optimum
formulation.
o Can trace and rectify problem in a remarkably easier
manner.
9/27/2015

8. 9/27/2015
PARAMETERS
PROBLEM TYPE
CONSTRAINED
UNCONSTRAINED
VARIABLES DEPENDENT
INDEPENDENT
Optimization Parameters

9. Problem Types
Unconstrained
• In unconstrained optimization problems there are no restrictions.
• For a given pharmaceutical system one might wish to make the hardest tablet
possible.
• The making of the hardest tablet is the unconstrained optimization problem.
Constrained
• The constrained problem involved in it, is to make the hardest tablet possible,
but it must disintegrate in less than 15 minutes.
9/27/2015

10. Variables
• Independent variables : The independent variables are under the control of
the formulator. These might include the compression force or the die cavity
filling or the mixing time.
• Dependent variables : The dependent variables are the responses or the
characteristics that are developed due to the independent variables. The
more the variables that are present in the system the more the
complications that are involved in the optimization.
9/27/2015

11. Example of Variables
9/27/2015

12. Classical Optimization
 Classical optimization is done by using the calculus to basic problem to find
the maximum and the minimum of a function.
 The curve in the fig represents the relationship between the response Y and
the single independent variable X and we can obtain the maximum and the
minimum. By using the calculus the graphical represented can be avoided. If
the relationship, the equation
for Y as a function of X, is available.
Y = f(X)
9/27/2015

13. Drawbacks
 Limited applications
• Problems that are too complex.
• They do not involve more than two variables.
 For more than two variables graphical representation is
impossible.
9/27/2015

14. Applied Optimization Methods
9/27/2015
Applied
optimization
Lagrangian
Method
Search
Method
Simplex
Lattice
Method
EVOP
METHOD

15. EVOP Method(Evolutionary Operation)
• Make very small changes in formulation repeatedly.
• The result of changes are statistically analyzed.
• If there is improvement, the same step is repeated until further
change doesn’t improve the product.
Where we have to select this technique?
This technique is especially well suited to a production situation.
The process is run in a way that is both produce a product that
meets all specifications and (at the same time) generates
information on product improvement.
9/27/2015

16.  Advantages:
• generates information on product development.
• predict the direction of improvement.
• Help formulator to decide optimum conditions for the formulation
and process.
 Limitations:
• More repetition is required
• Time consuming
• Not efficient to finding true optimum
• Expensive to use.
9/27/2015

17. • Example: In this example, A formulator can change the concentration
of binder and get the desired hardness.
9/27/2015

18. SIMPLEX Method
 A simplex is a geometric figure, defined by no. of points or
vertices equal to one more than no. of factors examined.
 Once the shape of a simplex has been determined, the
method can employ a simplex of fixed size or of variable
sizes that are determined by comparing the magnitudes of
the responses after each successive calculation
It is of two types:
A. Basic Simplex Method
B. Modified Simplex Method.
9/27/2015

19. SIMPLEX LATTICE
• It is an experimental techniques & mostly used in analytical rather than
formulation & processing.
Simplex is a geometric figure that has one more point than the number of
factors.
• e.g-If 2 independent variables then simplex is represented as triangle.
• The strategy is to move towards a better response by moving away from
worst response.
• Applied to optimize CAPSULES, DIRECT COMPRESSION TABLET),
liquid systems (physical stability).
• It is also called as Downhill Simplex / Nelder-Mead Method.
9/27/2015

20.  The simplex method is especially appropriate when:
• Process performance is changing over time.
• More than three control variables are to be changed.
• The process requires a fresh optimization with each new lot of
material.
 The simplex method is based on an initial design of k+1, where k is
the number of variables. A k+1 geometric figure in a k-dimensional
space is called a simplex. The corners of this figure are called vertices.
9/27/2015

21. In simplex lattice, the response may be plotted as 2D (contour plotted) or 3D plots (response
surface methodology)
9/27/2015

22. Advantage
• This method will find the true optimum of a response with
fewer trials than the non-systematic approaches or the one-
variable-at-a-time method.
Limitations :
• There are sets of rules for the selection of the sequential
vertices in the procedure.
• Requires mathematical knowledge.
9/27/2015

23. LAGRANGIAN Method
o It represents mathematical techniques.
o It is an extension of classic method.
o applied to a pharmaceutical formulation and processing.
o This technique follows the second type of statistical design
o This technique require that the experimentation be completed before
optimization so that the mathematical models can be generates
9/27/2015

24. • Determine constraints.
 Determine objective formulation.
• Change inequality constraints to equality constraints.
• Form the Lagrange function F.
• Partially differentiate the lagrange function for each
variable & set derivatives equal to zero.
• Solve the set of simultaneous equations.
• Substitute the resulting values in objective functions.
9/27/2015
Steps involved

25. SEARCH Method
oUnlike the Lagrangian method, do not require differentiability of
the objective function.
oIt is defined by appropriate equations.
o Used for more than two independent variables.
oThe response surface is searched by various methods to find the
combination of independent variables yielding an optimum.
oIt take five independent variables into account and is computer
assisted.
oPersons unfamiliar with mathematics of optimization & with no
previous computer experience could carryout an optimization
study.
9/27/2015

26. Advantages:
o Takes five independent variables in to account
o Person unfamiliar with the mathematics of optimization and with no
previous computer experience could carry out an optimization study.
o It do not require continuity and differentiability of function
Disadvantage:
o One possible disadvantage of the procedure as it is set up is that not
all pharmaceutical responses will fit a second-order regression
model.
9/27/2015

27. New Network for Optimization
Artificial Neural Network & optimization of pharmaceutical
formulation-
• ANN has been entered in pharmaceutical studies to forecast the
relationship b/w the response variables &casual factors . This is
relationship is nonlinear relationship.
• ANN is most successfully used in multi objective simultaneous
optimization problem.
• Radial basis functional network (RBFN) is proposed
simultaneous optimization problems.
• RBFN is an ANN which activate functions are RBF.
• RBF is a function whose value depends on the distance from the
Centre or origin.
9/27/2015

28. Formulation and Processing
Clinical Chemistry
Medicinal Chemistry
High Performance Liquid Chromatographic
Analysis
Formulation of Culture Medium in Virological
Studies.
Study of Pharmacokinetic Parameters.
APPLICATIONS
9/27/2015

29. Uses
9/27/2015
Provide solution to large scale manufacturing
problems.
Provides string assurances to regulatory agencies
superior drug product quality.
In microencapsulation process.
Improvement of physical & biological properties by
modification.

30. Conclusion
o Optimization techniques are a part of development process.
o The levels of variables for getting optimum response is evaluated.
o Different optimization methods are used for different optimization
problems.
o Optimization helps in getting optimum product with desired
bioavailability criteria as well as mass production.
o More optimum the product = More the company earns in profits !!!
9/27/2015

31. References
• Jain N. K., Pharmaceutical product development, CBS publishers and distributors, 1st
edition,297-302, 2006.
• Cooper L. and Steinberg D., Introduction to methods of optimization, W.B.Saunders,
Philadelphia, 1970, 1st Edition, 301-305.
• Bolton. S., Stastical applications in the pharmaceutical science, Varghese publishing
house,3rd edition, 223.
• Deming S.N. and King P. G., Computers and experimental optimization,
Research/Development, vol-25 (5),22-26, may 1974.
• Rubinstein M. H., Manuf. Chem. Aerosol News,30, Aug 1974.
• Digaetano T.N., Bull.Parenter.Drug Assoc., vol-29,183, 1975.
• Spendley, W., Sequential application of simplex designs in optimization and
evolutionary operation, Technometrics, Vol- 4 441–461, 1962.
• Forner D.E., Mathematical optimization techniques in drug product design and
process analysis, Journal of pharmaceutical sciences. , vol-59 (11),1587-1195,
November 1970.
9/27/2015

32. 9/27/2015