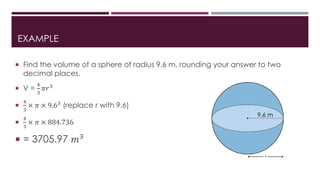
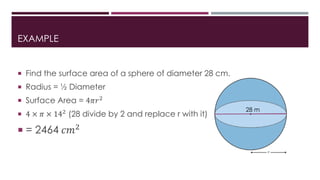
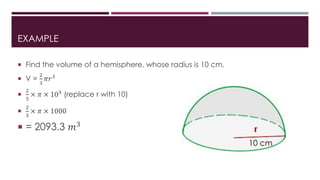
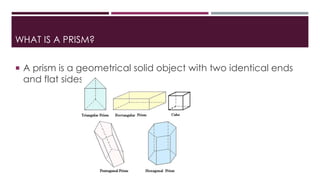
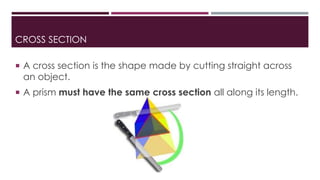
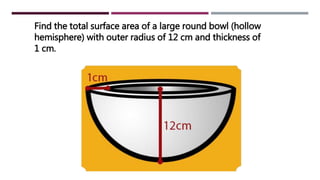
The document defines and provides properties of spheres, hemispheres, and prisms. It gives the formulas to calculate the volume and surface area of spheres (V=4/3πr^3, SA=4πr^2), hemispheres (V=2/3πr^3, SA=3πr^2), and prisms (V=Base Area x Length, SA=(2 x Base Area) + (Base Perimeter x Length)). Examples are included to demonstrate how to use the formulas to find the volume and surface area of each shape given specific values. The document concludes by providing the step-by-step working to find the total surface area of a hollow hemisphere with an outer radius of