Structural Theory II (Part 2/2)

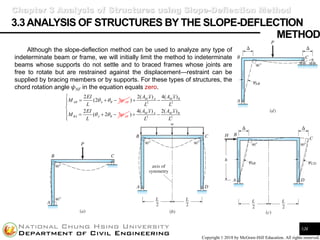
Shieh-Kung
Huang
Copyright © 2018 by McGraw-Hill Education. All rights reserved.
3.3ANALYSIS OF STRUCTURES BY THE SLOPE-DEFLECTION
126
Although the slope-deflection method can be used to analyze any type of
indeterminate beam or frame, we will initially limit the method to indeterminate
beams whose supports do not settle and to braced frames whose joints are
free to rotate but are restrained against the displacement—restraint can be
supplied by bracing members or by supports. For these types of structures, the
chord rotation angle 𝜓NF in the equation equals zero.
Chapter 3 Analysis of Structures using Slope-Deflection Method
METHOD
3
2
(2
AB A B AB
EI
M
L
 

= + − 2 2
2( ) 4( )
2
( 3
) M A M B
BA A B AB
A x A x
L L
EI
M
L

 
+ −
= +  − 2 2
4( ) 2( )
) M A M B
A x A x
L L




 + −



Shieh-Kung
Huang
127
The basic steps of the slope-deflection method, which were discussed in last section, are
summarized briefly below:
1. Identify all unknown joint displacements (rotations) to establish the number of unknowns.
2. Use the slope-deflection equation to express all member end moments in terms of joint rotations and
the applied loads.
3. At each joint, except fixed supports, write the moment equilibrium equation, which states that the
sum of the moments (applied by the members framing into the joint) equals zero. An equilibrium
equation at a fixed support, which reduces to the identity 0 = 0, supplies no useful information. The
number of equilibrium equations must equal the number of unknown displacements.
As a sign convention, clockwise moments on the ends of the members are assumed to be positive. If
a moment at the end of a member is unknown, it must be shown clockwise on the end of a member.
The moment applied by a member to a joint is always equal and opposite in direction to the moment
acting on the end of the member. If the magnitude and direction of the moment on the end of a
member are known, they are shown in the actual direction.
4. Substitute the expressions for moments as a function of displacements (see step 2) into the
equilibrium equations in step 3, and solve for the unknown displacements.
5. Substitute the values of displacement in step 4 into the expressions for member end moment in step
2 to establish the value of the member end moments. Once the member end moments are known,
the balance of the analysis—drawing shear and moment curves or computing reactions, for
example—is completed by statics.
METHOD

Shieh-Kung
Huang
128
METHOD

Shieh-Kung
Huang
129
METHOD

Shieh-Kung
Huang
130
METHOD
In the end, please identify steps 1 to 5!!!

Shieh-Kung
Huang
131
METHOD

Shieh-Kung
Huang
132
METHOD

Shieh-Kung
Huang
133
METHOD

Shieh-Kung
Huang
134
METHOD

Shieh-Kung
Huang
135
METHOD

Shieh-Kung
Huang
136
METHOD

Shieh-Kung
Huang
137
METHOD

Shieh-Kung
Huang
138
METHOD

Shieh-Kung
Huang
3.4ANAL
YSISOFSTRUCTURESTHA
TAREFREETOSIDESWA
Y
139
Thus far we have used the slope-deflection method to analyze indeterminate beams and frames with
joints that are free to rotate but which are restrained against displacement. We now extend the method to
frames whose joints are also free to sidesway, that is, to displace laterally.
Since we have written equations of moment in the
solution of previous problems, we will only discuss the
second type of equilibrium equation—the shear equation.
h


=
1 1
2 2
0 0
0 0
0
AB BA
A AB BA
CD DC
D CD DC
CD DC
AB BA
x
M M
M M M V h V
h
M M
M M M V h V
h
M M
M M
F Q
h h
+

= = + − =  =



+
 = = + − =  =


+
+
 = = + +




Shieh-Kung
Huang
3.4ANAL
YSISOFSTRUCTURESTHA
TAREFREETOSIDESWA
Y
140

Shieh-Kung
Huang
3.4ANAL
YSISOFSTRUCTURESTHA
TAREFREETOSIDESWA
Y
141

Shieh-Kung
Huang
3.4ANAL
YSISOFSTRUCTURESTHA
TAREFREETOSIDESWA
Y
142

Shieh-Kung
Huang
3.4ANAL
YSISOFSTRUCTURESTHA
TAREFREETOSIDESWA
Y
143

Shieh-Kung
Huang
3.4ANAL
YSISOFSTRUCTURESTHA
TAREFREETOSIDESWA
Y
144
?
?

Shieh-Kung
Huang
3.4ANAL
YSISOFSTRUCTURESTHA
TAREFREETOSIDESWA
Y
145

Shieh-Kung
Huang
3.4ANAL
YSISOFSTRUCTURESTHA
TAREFREETOSIDESWA
Y
146
?

Shieh-Kung
Huang
3.4ANAL
YSISOFSTRUCTURESTHA
TAREFREETOSIDESWA
Y
147
?

Shieh-Kung
Huang
3.4ANAL
YSISOFSTRUCTURESTHA
TAREFREETOSIDESWA
Y
148

Shieh-Kung
Huang
3.5 KINEMATIC INDETERMINACY
149
To analyze a structure by the flexibility method, we first established the degree of indeterminacy of
the structure. The degree of statical indeterminacy determines the number of compatibility equations we
must write to evaluate the redundants, which are the unknowns in the compatibility equations.
In the slope-deflection method, displacements—both joint rotations and translations—are the
unknowns. As a basic step in this method, we must write equilibrium equations equal in number to the
independent joint displacements. The number of independent joint displacements is termed the degree of
kinematic indeterminacy.
To determine the kinematic indeterminacy, we simply count the number of
independent joint displacements that are free to occur.
• Degree of statical indeterminacy:
Number of redundants (compatibility equations)
• Degree of kinematic indeterminacy:
Number of independent joint displacements

Shieh-Kung
Huang
ANAL
YSISOFSTRUCTURESUSINGMOMENTDISTRIBUTIONMETHOD
Chapter Objectives
150
Students will be able to
1. Learn the moment distribution method for analyzing
indeterminate beams and frames.
2. Understand how joint equilibrium is achieved by unlocking
and locking joints in succession
3. Distribute moments to both ends of all members framing to
the joint until all joints achieve equilibrium.
4. Learn the procedure to analyze beams and frames with
sway inhibited, and then extend the procedure to sway
uninhibited.
5. Extend the use of moment distribution method to beams
and frames with nonprismatic members.
CHAPTER 4
4.1 Development of the Moment Distribution
Method
4.2 Summary of the Moment Distribution
Method with No Joint Translation
4.3 Analysis of Beams by Moment Distribution
4.4 Modification of Member Stiffness
4.5 Analysis of Frames That Are Free to
Sidesway
4.6 Analysis of an Unbraced Frame for General
Loading
4.7 Analysis of Multistory Frames
4.8 Nonprismatic Members
Chapter Outline

Shieh-Kung
Huang
4.1DEVELOPMENTOFTHEMOMENTDISTRIBUTIONMETHOD
Introduction of Moment Distribution Method
151
Chapter 4 Analysis of Structures using Moment Distribution Method
Moment distribution, developed by Hardy Cross in the early 1930s, is a procedure for establishing the
end moments in members of indeterminate beams and frames with a series of simple computations.
The moment distribution—a commonly used hand method for analyzing beams and frames rapidly—
is also based on the stiffness formulation.
In the moment distribution method, we imagine that temporary restraints are applied to all joints of a
structure that are free to rotate or to displace. We apply hypothetical clamps to prevent rotation of joints
and introduce imaginary rollers to prevent lateral displacements of joints (the rollers are required only for
structures that sidesway).

Shieh-Kung
Huang
Unbalanced and Distributed End Moments
152
In the first step, we imagine that joint
B is locked against rotation by a large
clamp. The application of the clamp
produces two fixed-end beams.
• Unbalanced Moment
To prevent the joint from rotating, the
clamps must apply a moment to the joint
that is equal and opposite to FEMBA. The
moment that develops in the clamp is
called the unbalanced moment (UM). If
span BC were also loaded, the
unbalanced moment in the clamp would
equal the difference between the fixed-end
moments applied by the two members
framing into the joint.
• Distributed End Moments
If we now remove the clamp, joint B
will rotate and additional moments, labeled
DEMBC, COMBC, DEMBA, and COMBA,
develop at the ends of members AB and
BC. These moments, called the distributed
end moments (DEMs), are opposite in
sense to the unbalanced moment.

Shieh-Kung
Huang
Carryover Moments
153
In all moment distribution computations, the sign convention will be the same as that used in the
slope-deflection method: Rotations of the ends of members and moments applied to the ends of members
are positive in the clockwise direction and negative in the counterclockwise direction.
• Carryover Moments
The moments produced at the A end of member AB and at the C end of member BC by the rotation of
joint B are called carryover moments (COMs).
In the equation, the term 4EIAB/LAB is termed the absolute flexural stiffness of the B end of member AB. It
represents the moment required to produce a rotation of 1 rad at B when the far end at A is fixed.
Since both the carryover moment and the distributed end moment given by above equations are
functions of θB—the only variable that has
a plus or minus sign—both moments have
the same sense, that is, positive if θB is
clockwise and negative if θB is opposite.
DEM
DEM
COM COM
2
2
(2 )
(2 ) FEM
Member and Member
2 2
( ) FEM ( )
BC
BA
BA BC
BC
AB
BC B
BA B BA
BC
AB
AB BC
AB B BA CB B
AB BC
EI
EI
M
M
L
L
AB CB
EI EI
M M
L L


 


=
= + 



 
 
 
= + =
 
 
 

Shieh-Kung
Huang
Carryover and Distribution Factor
154
• Carryover Factor
If we compare the value of MBC with MCB, we reach the conclusion; that is, the carryover moment
equals one-half the distributed end moment. Therefore, the carryover factor equals one-half for prismatic
members. It will be shown latter that this factor will not be equal to one-half for nonprismatic members.
• Distribution Factor
We can establish the magnitude of the distributed end moments at joint B as
The ratio is called the distribution factor (DFBA) for member AB.
4 4
UM DEM DEM 4 ( )
DEM UM DF
( ) ( )
DEM DF (UM)
UM
where
DEM DF (UM)
4 ( )
DEM UM DF
( ) ( )
AB BC
BA BC B B AB BC B
AB BC
AB AB
BA AB
AB BC AB BC
BA AB
B
BC BC
BC BC
AB BC
BC BC
AB BC AB BC
EI EI
E K K
L L
K K
K K K K
K K
E K K
K K K K
  

= + = + = +
 
= =
 
+ +
=

 
 =  
  
=
+ 
 
= =
 
+ +
 

Shieh-Kung
Huang
4.2 SUMMARY OF THE MOMENT DISTRIBUTION METHOD
155
The basic steps of the moment distribution method, which were discussed in last section, are
summarized briefly below:
1. Draw a line diagram of the structure to be analyzed.
2. At each joint that is free to rotate, compute the distribution factor for each member and record in a
box on the line diagram adjacent to the joint. The sum of the distribution factors at each joint must
equal 1.
3. Write down the fixed-end moments at the ends of each loaded member. As the sign convention we
take clockwise moments on the ends of members as positive and counterclockwise moments as
negative.
4. Compute the unbalanced moment at the first joint to be unlocked. The unbalanced moment at the
first joint is the algebraic sum of the fixed end moments at the ends of all members framing into the
joint. After the first joint is unlocked, the unbalanced moments at the adjacent joints will equal the
algebraic sum of fixed-end moments and any carryover moments.
5. Unlock the joint and distribute the unbalanced moment to the ends of each member framing into the
joint. The distributed end moments are computed by multiplying the unbalanced moment by the
distribution factor of each member. The sign of the distributed end moments is opposite to the sign of
the unbalanced moment.
6. Write the carryover moments at the other end of the member. The carryover moment has the same
sign as the distributed end moment but is one-half as large.
7. Replace the clamp and proceed to the next joint to distribute moments there. The analysis is finished
when the unbalanced moments in all clamps are either zero or close to zero.
WITH NO JOINT TRANSLATION

Shieh-Kung
Huang
4.3 ANALYSIS OF BEAMS BY MOMENT DISTRIBUTION
156
To illustrate the moment distribution procedure, we will analyze the two-span continuous beam first.
Since only the joint at support B is free to rotate, a complete analysis requires only a single distribution of
moments at joint B. In succeeding problems we consider structures that contain multiple joints that are
free to rotate.

Shieh-Kung
Huang
157

Shieh-Kung
Huang
158

Shieh-Kung
Huang
159

Shieh-Kung
Huang
160

Shieh-Kung
Huang
161

Shieh-Kung
Huang
162
What if we start to distribute the moment from joint C?

Shieh-Kung
Huang
163
What if we distribute the moment from both joint B and joint C?

Shieh-Kung
Huang
164

Shieh-Kung
Huang
165

Shieh-Kung
Huang
4.4 MODIFICATION OF MEMBER STIFFNESS
Cases of Hinges
166
We can often reduce the number of cycles of moment distribution required to analyze a continuous
structure by adjusting the flexural stiffness of certain members. In this section we consider members
whose ends terminate at an exterior support consisting of either a pin or roller.
To measure the influence of end conditions on the flexural stiffness of a beam, we can compare the
moment required to produce a unit rotation (1 rad) of the end of a member for various end conditions.
Comparing above examples, we see that a beam loaded by a moment at one end whose far end is pinned
is three-fourths as stiff with respect to resistance to joint rotation as a beam of the same dimensions
whose far end is fixed.

Shieh-Kung
Huang
167

Shieh-Kung
Huang
168

Shieh-Kung
Huang
169

Shieh-Kung
Huang
170

Shieh-Kung
Huang
171

Shieh-Kung
Huang
172

Shieh-Kung
Huang
Cases of Single and Double Curvature Bending
173
If a member is bent into double curvature by equal end moments, the resistance to rotation increases
because the moment at B, the far end, rotates the near end A in a direction opposite in sense to the
moment at A.
Comparing example in the last slide, we find that the absolute stiffness for a member bent in double
curvature by equal end moments is 50 percent greater than the stiffness of a beam whose far end is fixed
against rotation.
If a flexural member is acted on by equal values of end moments, producing single-curvature bending,
the effective bending stiffness with respect to the A end is reduced because the moment at the far end
(the B end) contributes to the rotation at the A end.
Comparing example in the last slide, we find that the absolute stiffness of a member bent into single
curvature by equal end moments has an effective stiffness that is 50 percent smaller than that of a beam
whose far end is fixed against rotation.
6
AB
EI
M
L
=
2
AB
EI
M
L
=

Shieh-Kung
Huang
Cases of Single and Double Curvature Bending
174
6EI
L
=
2EI
L
=

Shieh-Kung
Huang
Other Cases
175
• Stiffness of a Cantilever
Note that once you modified the stiffness, you don’t need to carryover the moment again (no COM).

Shieh-Kung
Huang
176

Shieh-Kung
Huang
177

Shieh-Kung
Huang
178

Shieh-Kung
Huang
179
What if we just don’t use the modified stiffness?
Case 1: no consideration of hinge and symmetry
There is always some moment at hinge!!!
360
20
18
600
15
40
AB AB
AB CD
AB
BC BC
BC
BC
E I
K K E E
L
E I
K E E
L
= = = =
= = =

Shieh-Kung
Huang
180
What if we just don’t use the modified stiffness?
Case 2: no consideration of symmetry
Still not over yet!!!
3 3 360
15
4 4 18
600
15
40
AB AB
AB CD
AB
BC BC
BC
BC
E I
K K E E
L
E I
K E E
L
= = = =
= = =

Shieh-Kung
Huang
Other Cases
181
• Support Settlements, Fabrication Errors, and Temperature Change
Moment distribution and the slope-deflection equation provide an effective combination for
determining the moments created in indeterminate beams and frames by fabrication errors, support
settlements, and temperature change. In this application the appropriate displacements are introduced
into the structure while simultaneously all joints that are free to rotate are locked by clamps against
rotation in their initial orientation. Locking the joints against rotation ensures that the changes in slope
at the ends of all members are zero and permits the end moments produced by specified values of
displacement to be evaluated by the slope-deflection equation. To complete the analysis, the clamps
are removed and the structure is allowed to deflect into its final equilibrium position.
In Example 11.7 we use this procedure to determine the moments in a structure whose supports
are not located in their specified position—a common situation that frequently occurs during the
construction. In Example 11.8 the method is used to establish the moments created in an
indeterminate frame by a fabrication error.
2 (2 3 ) FEM where
NF N F NF NF
I
M EK K
L
  
= + − + =
2 (2 3 ) FEM
2 ( 2 3 ) FEM
AB A B AB AB
BA A B AB BA
M EK
M EK
  
  
= + − +


= + − +

2 2
2 2
2( ) 4( )
2
(2 3 )
4( ) 2( )
2
( 3 )
M A M B
AB A B AB
M A M B
BA A B AB
A x A x
EI
M
L L L
A x A x
EI
M
L L L
  
  

= + − + −



 = +  − + −



Shieh-Kung
Huang
182

Shieh-Kung
Huang
183

Shieh-Kung
Huang
184

Shieh-Kung
Huang
185

Shieh-Kung
Huang
186

Shieh-Kung
Huang
4.5 ANALYSIS OF FRAMES THAT ARE FREE TO SIDESWAY
187
All structures that we have analyzed thus far contained joints that were free to rotate but not translate.
Frames of this type are called braced frames. When certain joints of an unbraced frame are free to
translate, the designer must include the moments created by chord rotations.
Typically, a unit displacement is introduced. To hold the structure in the deflected position, temporary
restraints are introduced. These restraints consist of a roller at B to maintain the 1. displacement and
clamps at A, B, and C to prevent joint rotation.
Clamps are now removed and moments distributed until the
structure relaxes into its equilibrium position. In the equilibrium position,
the temporary roller at B applies a lateral force S to the frame. The force
required to produce a unit displacement of the frame, denoted by S, is
termed a stiffness coefficient.
2
2 6
( 3 )
NF NF
EI EI
M
L L

= − = −

Shieh-Kung
Huang
188

Shieh-Kung
Huang
189

Shieh-Kung
Huang
190

Shieh-Kung
Huang
191

Shieh-Kung
Huang
192

Shieh-Kung
Huang
4.6ANALYSIS OFAN UNBRACED FRAME FOR GENERAL
193
LOADING
If a structure that is loaded between joints undergoes sidesway, we begin the analysis by introducing
temporary restraints (holding forces) to prevent joints from translating.
The restrained structure is then analyzed by moment distribution for the loads applied between joints.
After the shears in all members are computed from free bodies of individual members, the holding forces
are evaluated using the equations of statics by considering the equilibrium of members and/or joints.
Superposition of the Case A and Case B analyses produces results equivalent to the original case.

Shieh-Kung
Huang
194
LOADING

Shieh-Kung
Huang
195
LOADING

Shieh-Kung
Huang
196
LOADING

Shieh-Kung
Huang
197
LOADING

Shieh-Kung
Huang
198
LOADING

Shieh-Kung
Huang
199
LOADING

Shieh-Kung
Huang
4.7 ANALYSIS OF MULTISTORY FRAMES
200
To extend moment distribution to the analysis of multistory frames,
we must add one sidesway correction for each independent degree of
sidesway. Since the repeated analysis of the frame for the various cases
becomes time consuming, we will only outline the method of analysis,
so the student is aware of the complexity of the solution. In practice,
engineers today use computer programs to analyze frames of all types.

Shieh-Kung
Huang
INFLUENCELINESFORSTATICALLYINDETERMINATESTRUCTURES
Chapter Objectives
201
1. understand the concept of and the need for influence lines
2. learn the Müller–Breslau principle to graphically construct
influence lines
3. draw the influence line for a statically indeterminate beams
4. draw the influence line for a statically indeterminate trusses
CHAPTER 5
5.1 Influence Lines
5.2 Müller–Breslau Principle
5.3 Qualitative Influence Lines for Indeterminate
Beams and Frames
5.4 Influence Lines for Indeterminate Trusses
Chapter Outline

Shieh-Kung
Huang
5.1 INFLUENCE LINES
202
Chapter 5 Influence Lines for Statically Indeterminate Structures
If a structure is to be safely designed, we must proportion its members and joints so that the
maximum force at each section produced by load is less than or equal to the available capacity.
To establish maximum design forces at critical sections produced by moving loads, we frequently
construct influence lines.
An influence line is a diagram whose ordinates, which are plotted as a function of distance along the
span, give the value of an internal force, a reaction, or a displacement at a particular point in a structure
as a unit load of 1 kip or 1 kN moves across the structure.
Once the influence line is constructed, we can use it to determine where to place live load on a
structure to maximize the force (shear, moment, etc.) for which the influence line is drawn, and to evaluate
the magnitude of the force (represented by the influence line) produced by the live load.
Although an influence line represents the action of a single moving load, it can also be used to
establish the force at a point produced by several concentrated loads or by a uniformly distributed load.

Shieh-Kung
Huang
5.2 MÜ LLER–BRESLAU PRINCIPLE
203
The Müller–Breslau principle provides a simple procedure for establishing the shape of influence
lines for the reactions or the internal forces (shear and moment) in beams.
The principle states:
The influence line for any reaction or internal force (shear, moment) corresponds to the deflected shape of
the structure produced by removing the capacity of the structure to carry that force and then introducing
into the modified (or released) structure a unit deformation that corresponds to the restraint removed.

Shieh-Kung
Huang
5.2 MÜ LLER–BRESLAU PRINCIPLE
204

Shieh-Kung
Huang
5.3 QUALITATIVE INFLUENCE LINES FOR INDETERMINATE
205
In this section we illustrate the use of the Müller–Breslau method to construct qualitative influence
lines for a variety of forces in continuous beams and frames.
As described in the Müller–Breslau method, we first remove the capacity of the structure to carry the
function represented by the influence line. At the location of the release, we introduce a displacement that
corresponds to the restraint released. The resulting deflected shape is the influence line to some scale.
BEAMSAND FRAMES

Shieh-Kung
Huang
206
In the following examples, we use the Müller–Breslau principle to sketch qualitative influence lines for
a variety of forces and reactions in a three-span continuous beam.
BEAMSAND FRAMES

Shieh-Kung
Huang
207
BEAMSAND FRAMES

Shieh-Kung
Huang
208
BEAMSAND FRAMES

Shieh-Kung
Huang
209
BEAMSAND FRAMES

Shieh-Kung
Huang
210
BEAMSAND FRAMES

Shieh-Kung
Huang
211
BEAMSAND FRAMES

Shieh-Kung
Huang
212
BEAMSAND FRAMES

Shieh-Kung
Huang
213
BEAMSAND FRAMES

Shieh-Kung
Huang
214
BEAMSAND FRAMES

Shieh-Kung
Huang
215
BEAMSAND FRAMES

Shieh-Kung
Huang
216
BEAMSAND FRAMES

Shieh-Kung
Huang
217
BEAMSAND FRAMES

Shieh-Kung
Huang
218
BEAMSAND FRAMES

Shieh-Kung
Huang
5.4 INFLUENCE LINES FOR INDETERMINATE TRUSSES
219
Using the basic definition, influence lines of a truss that is indeterminate to the first degree is
presented in the following example. The flexibility method is used to analyze the truss.

Shieh-Kung
Huang
220

Shieh-Kung
Huang
221

Shieh-Kung
Huang
222

Shieh-Kung
Huang
INTRODUCTION TO THE GENERAL STIFFNESS METHOD
Chapter Objectives
223
1. Learn the transition from the classical to matrix methods of
structural analysis
2. Understand the differences between the classical flexibility
method and stiffness (slope-deflection) method
3. Extend the stiffness method to a general stiffness method
for analyzing an indeterminate structure with only one
degree of kinematic indeterminacy.
CHAPTER 6
6.1 Comparison between Flexibility and
Stiffness Methods
6.2 Analysis of an Indeterminate Structure by
the General Stiffness Method
Chapter Outline

Shieh-Kung
Huang
6.1 COMPARISON BETWEEN FLEXIBILITYAND STIFFNESS
Flexibility Method
224
Chapter 6 Introduction to the General Stiffness Method
This chapter provides a transition from classical methods of hand analysis, such as the flexibility
method, slope-deflection method, or moment distribution method, to analysis by computer using general
stiffness method.
METHODS
10
1 10 11 1 1
11
20 2 2
2 2 2 2
1
11 1 21 2 1 2
1 1 2 2 1 1 2 2
0 0
F F
F L PL
A E A E
F
F L F L L L
AE A E AE A E



 =   + =  = −
 = − = −
+ +
In the flexibility method, we write compatibility
equations in terms of unknown redundant forces.
In the stiffness method, we write equilibrium equations
in terms of unknown joint displacements.
• Analysis using Flexibility Method
To analyze the structure, we select the horizontal
reaction F1 at joint 1 as the redundant. We produce a
stable determinate released structure by imagining that
the pin at joint 1 is replaced by a roller.
To determine the reaction F1, we write an equation
of compatibility based on the geometric requirement
that the horizontal displacement at support 1 must be
zero.

Shieh-Kung
Huang
Since the restraining force exerted by the
bars is a linear function of the displacement of
joint 2, the actual joint displacement Δ2 can be
determined by writing the equilibrium equation
for forces in the horizontal direction at joint 2.
The quantity K2 is called a stiffness
coefficient. If the two bars are treated as a
large spring, the stiffness coefficient measures
the resistance (or stiffness) of the
system to deformation.
6.1 COMPARISON BETWEEN FLEXIBILITYAND STIFFNESS
Stiffness Method
225
• Analysis using Stiffness Method
The structure will now be reanalyzed by the stiffness method. Since only joint 2 is free to displace,
the structure is kinematically indeterminate to the first degree.
METHODS
1 1 1 1
1 1 2
1 1
1 2 2
2 2 2 2
2 2 2
2 2
(T)
and
(C)
AE AE
F L
L L
L L
A E A E
F L
L L

=  = 


 =  =  
 =  = 


1 1 2 2
1 2 2 2
1 2
2
1 1 2 2 2
1 2
0 0
AE A E
P F F P
L L
P P
AE A E K
L L
− − =  −  −  =
  = =
+

Shieh-Kung
Huang
6.2ANALYSIS OFAN INDETERMINATE STRUCTURE BY THE
226
The next example shows a continuous beam of constant cross section. Since the only unknown
displacement of the continuous beam is the rotation θ2 that occurs at joint 2, the structure is kinematically
indeterminate to the first degree.
GENERAL STIFFNESS METHOD

Shieh-Kung
Huang
6.2ANALYSIS OFAN INDETERMINATE STRUCTURE BY THE
Summary of the General Stiffness Method
227
The analysis of the last example is based on the superposition of two cases.
− In case 1, we clamp all joints that are free to rotate and apply the load. The load creates fixed-end
moments in the beam and an equal moment in the clamp. At this point the structure is in equilibrium
with the load; however, the joint has been restrained by a clamp and not allowed to rotate.
− To eliminate the clamp, we must remove it and allow the joint to rotate. This rotation will produce
additional moments in the members. Since we do not know the magnitude of the rotation, in a
separate case 2, we arbitrarily introduce a unit rotation of 1 rad and clamp the beam in the deflected
position. The case 2 clamp now applies a moment, termed a stiffness coefficient, which holds the
beam in the rotated position.
If we now multiply the forces and displacements in case 2 by the actual magnitude of the joint rotation
θ2, all forces and displacements (including the moment in the clamp and the rotation at joint 2) will be
scaled proportionally to the correct value; i.e., the sum of the moments in the clamp from the two cases
must equal zero.
Accordingly the value of θ2 can now be determined by writing an equilibrium equation that states the
sum of the moments in the clamp, from case 1 and case 2, must equal zero.
Once θ2 is known, all forces in case 2 can be evaluated and added directly to those of case 1.
GENERAL STIFFNESS METHOD

Shieh-Kung
Huang
MATRIXANAL
YSISOFTRUSSESBYTHEDIRECTSTIFFNESSMETHOD
Chapter Objectives
228
1. Learn how to establish the matrix form of equilibrium
equations for a truss
2. Learn how to partition the matrices such that both the
unknown joint displacements and unknown reactions can
be solved by matrix operation
3. Learn how to establish the structure stiffness matrix either
by basic mechanics or by individual member stiffness
matrices
4. Construct member stiffness matrix by using either the local
or global coordinate system
5. Learn how to convert a member stiffness matrix from local
to global coordinate system by the concept of coordinate
transformation
CHAPTER 7
7.1 Member and Structure Stiffness Matrices
7.2 Construction of a Member Stiffness Matrix
for an Individual Truss Bar
7.3 Assembly of the Structure Stiffness Matrix
7.4 Solution of the Direct Stiffness Method
7.5 Member Stiffness Matrix of an Inclined
Truss Bar
7.6 Coordinate Transformation of a Member
Stiffness Matrix
Chapter Outline

Shieh-Kung
Huang
7.1 MEMBER AND STRUCTURE STIFFNESS MATRICES
229
Chapter 7 Matrix Analysis of Trusses by the Direct Stiffness Method
To permit the stiffness method to be programmed automatically from the input data (i.e., joint
coordinates, member properties, joint loads, and so forth), we now introduce a slightly different procedure
for generating the structure stiffness matrix K. In this modified procedure we generate the member
stiffness matrix k of individual truss members and then combine these matrices to form the structure
stiffness matrix K.
The member stiffness matrix for an axially loaded bar relates the axial forces at the ends of the
member to the axial displacements at each end. The elements of the member stiffness matrix are initially
expressed in terms of a local or member coordinate system whose x′ axis is collinear with that of the
member’s longitudinal axis.
Since the inclination of the longitudinal axes of individual bars usually varies, before we can combine
the member stiffness matrices, we must transform their properties from the individual member coordinate
systems to that of a single global coordinate system for the structure.
When the local coordinate system of all truss bars coincides with the global coordinate system, the
next procedure is to assemble the structure stiffness matrix from the member stiffness matrices. After the
structure stiffness matrix is established, the last procedure is to determine the unknown nodal
displacements, reactions, member deformations, and forces.
Member stiffness matrix in
Local Coordinate System, k′
Global Coordinate System, k
Structure stiffness matrix in
Global Coordinate System, K

Shieh-Kung
Huang
7.2 CONSTRUCTION OFAMEMBER STIFFNESS MATRIX FOR
230
• For Truss with A Displaced Node 1 (Case 1)
• For Truss with A Displaced Node 2 (Case 2)
• For Truss with An Arbitrary Nodal Displacement (General Case)
The prime is added to k′ to indicate that the formulation is in terms of
the member’s local coordinates x′ and y′.
AN INDIVIDUALTRUSS BAR
11 1 21 1
and
AE AE
Q Q
L L
=  = − 
12 2 22 2
and
AE AE
Q Q
L L
= −  = 
1 11 12 1 2
1 1
2 2
2 21 22 1 2
or
AE AE AE AE
Q Q Q
Q
L L L L
Q
AE AE AE AE
Q Q Q
L L L L
  
= + =  −  −
   
   


 = =
 
    

   
 
 = + = −  +  −
 

  
Q k Δ
− We observe that the sum of the elements in each column of k′ equals
zero. This condition follows because the coefficients in each column
represent the forces produced by a unit displacement of one joint while
the other joint is restrained. Since the bar is in equilibrium in the x′
direction, the forces must sum to zero.
− In addition, all coefficients along the main diagonal must be positive
because these terms are associated with the force acting at that joint
at which a positive displacement is introduced into the structure, and
correspondingly the force is in the same (positive) direction as the
displacement.

Shieh-Kung
Huang
7.3 ASSEMBLY OF THE STRUCTURE STIFFNESS MATRIX
Superimposing Forces Produced by Nodal Displacements
231
If a structure consists of several bars and the local coordinate system of these bars coincides with the
global coordinate system, then the stiffness matrix K of the structure can be generated by either of the
two following methods:
− Superimposing Forces Produced by Nodal Displacements:
Introducing displacements at each joint with all other joints restrained
− Combining Member Stiffness Matrices
Combining the stiffness matrices of the individual bars
• Superimposing Forces Produced by Nodal Displacements
As shown in the figures, we introduce displacements at
each joint while all other joints are restrained and compute the
joint forces.
where Q is column matrix of nodal forces
Δ is column matrix of nodal displacements
K is structure stiffness matrix
1 11 12 13 1 1 1 2
2 21 22 23 1 1 2 2 2 3
3 31 32 33 2 2 3 3
1 1 1 1
2 1 1 2 2 2
3 2 2 3
( ) where
0
or
0
i i
i
i
Q Q Q Q k k
AE
Q Q Q Q k k k k k
L
Q Q Q Q k k
Q k k
Q k k k k
Q k k
= + + =  − 


= + + = −  + +  −  =

 = + + = −  + 

− 
     
     
 = − + −  =
     
     
− 
     
Q KΔ

Shieh-Kung
Huang
7.3 ASSEMBLY OF THE STRUCTURE STIFFNESS MATRIX
Combining Member Stiffness Matrices
232
• Combining Member Stiffness Matrices
The stiffness matrix of the structure in the figure can also be generated by combining the member
stiffness matrices of bars 1 and 2, as we mentioned in Section 7.2.
We construct a global xy coordinate system at joint 1 such
that this system coincides with the local x′y′ coordinate system
of individual bars. Because the x′ axis of each bar coincides with
the x axis in the global coordinate system, so k1 = k′1 and k2 = k′2.
Since the expanded matrices are of the same order, we can add their elements directly to
produce the structure stiffness matrix K.
The stiffness matrix is identical to that produced by method 1.
1 1 1 1
1 2 2 1 1 2 2 2
3 2 2 3
0
or
0
Q k k
Q k k k k
Q k k
− 
     
     
= +  = − + −  =
     
     
− 
     
K k k Q KΔ
1 1 1 1
12 1 12
2 1 1 2
2 2
2 2
23 2 23
3 3
2 2
Q k k
Q k k
Q k k
Q k k
− 
     

=  =
     
− 
     

−
   
 

=  =
   
  
−
 
   
Q k Δ
Q k Δ
1 2
1 1 1 1 1 1
2 1 1 2 2 2 2 2
3 3 3 2 2 3
0 0 0 0
0 and 0
0 0 0 0
Q k k Q
Q k k Q k k
Q Q k k
−  
           
           
= −  = − 
           
           
 − 
           
k k

Shieh-Kung
Huang
7.4 SOLUTION OF THE DIRECT STIFFNESS METHOD
233
Once the structure stiffness matrix K is assembled and the force-displacement relationship
established, we describe in this section how to evaluate the unknown joint displacement vector Δ and
support reactions of a structure.
The next step requires that all rows associated with the degrees of freedom be shifted to the top of
the matrix. (When a row is shifted upward, the corresponding column also needs to be shifted forward to
the left in a similar manner). The result of this reorganization and partitioning will permit us to express
equilibrium equations in terms of the following submatrices:
where Qf is matrix containing values of load at joints free to displace
Qs is matrix containing unknown support reactions
Δf is matrix containing unknown joint displacements
Δs is matrix containing support displacements
ff fs
f f
sf ss
s s
 
   
=  
   
   
 
K K
Q Δ
K K
Q Δ
1 1
where
and
f ff f fs s f ff f
s
s sf f ss s s sf f
f ff f s sf ff f
− −
= + =
 
 
 =
 
= + =
 
 
 = =
Q K Δ K Δ Q K Δ
Δ 0
Q K Δ K Δ Q K Δ
Δ K Q Q K K Q

Shieh-Kung
Huang
7.5MEMBERSTIFFNESSMATRIXOFANINCLINEDTRUSSBAR
234
In this section, we develop the member
stiffness matrix k for an inclined bar in terms of
global coordinates so that the direct stiffness
method can be extended to trusses with
diagonal members.
Treating xi, yi, xj, and yj as the coordinates
of joints i and j, respectively, sin ϕ and cos ϕ
can be expressed in terms of the coordinates
of nodes i and j as
2 2
sin and cos =
where ( ) ( )
j i j i
j i j i
y y x x
L L
L x x y y
 
− −
=
= − + −
2
2
cos cos
sin sin cos
cos
sin cos
ix i ix
iy i ix
jx ix ix
jy iy ix
F F k
F F k
F F k
F F k
 
  

 
= = 
= = 
= − = − 
= − = − 
2
2
sin cos
sin
sin cos
sin
ix iy
iy iy
jx iy
jy iy
F k
F k
F k
F k
 

 

= 
= 
= − 
= − 

Shieh-Kung
Huang
235
After assembling, we have
where Q is column matrix of nodal forces
Δ is column matrix of nodal displacements
k is member stiffness matrix in term
of global coordinates
2
2
cos
sin cos
cos
sin cos
ix jx
iy jx
jx jx
jy jx
F k
F k
F k
F k

 

 
= − 
= − 
= 
= 
2
2
sin cos
sin
sin cos
sin
ix jy
iy jy
jx jy
jy jy
F k
F k
F k
F k
 

 

= − 
= − 
= 
= 
2 2
2 2
2 2
2 2
or
where , sin , and cos
ix ix
iy iy
jx jx
jy jy
Q c sc c sc
Q sc s sc s
k
Q c sc c sc
Q sc s sc s
AE
k s c
L
 

   
 
− −
   
  
− −
   
 
= =
   
  
− −
   
 

− −
 
   
= = =
Q kΔ

Shieh-Kung
Huang
236
The axial displacement δi of joint i in the direction of the member’s longitudinal axis can be expressed
in terms of the horizontal and vertical components of displacement at joint i.
where T is a transformation matrix that converts the components of member end displacements in global
coordinates to the axial displacements in the direction of the member’s axis.
cos sin
cos sin
0 0
or
0 0
i ix iy ix iy
j jx jy jx jy
ix
i iy
j jx
jy
c s
c s
    
    


= + =  + 



= + =  + 



 
 

     
 = =
     

 
 
 

 
δ TΔ

Shieh-Kung
Huang
7.2 COORDINATE TRANSFORMATION OFAMEMBER
237
In Section 7.2, we derived the 2 by 2 stiffness member matrix k′ of a truss bar with respect to a local
coordinate system. And, we derived the 4 by 4 stiffness member matrix k with respect to a global
coordinate system in the last section. Actually, it is more commonly generated from the member stiffness
matrix k′ formulated in local coordinates, using a transformation matrix T constructed from the geometric
relationship between the local and global coordinate systems.
The equation used to perform the coordinate transformation is
where k is 4 by 4 member stiffness matrix referenced to global coordinates
k′ is 2 by 2 member stiffness matrix referenced to local coordinate system
T is transformation matrix, that is, matrix that converts the displacement vector Δ in global
coordinates to the axial displacement vector δ in the direction of bar’s longitudinal axis
STIFFNESS MATRIX
T

=
k T k T

Shieh-Kung
Huang
7.2 COORDINATE TRANSFORMATION OFAMEMBER
238
STIFFNESS MATRIX

Shieh-Kung
Huang
INTRODUCTIONOFMATRIXANALYSISFORBEAMSANDFRAMES
Chapter Objectives
239
1. Extend the direct stiffness method learned form trusses to
beams and frames
2. Learn how to establish the structure stiffness matrix either
by basic mechanics or by individual member stiffness
matrices
3. Construct member stiffness matrix as a 2 by 2, 4 by 4, or 6
by 6 matrix
4. Learn how to convert a member stiffness matrix from local
to global coordinate system by using the concept of
coordinate transformation
CHAPTER 8
8.1 Structure Stiffness Matrix
8.2 The 2 by 2 Rotational Stiffness Matrix for a
Flexural Member
8.3 The 4 by 4 Member Stiffness Matrix in Local
Coordinates
8.4 The 6 by 6 Member Stiffness Matrix in Local
Coordinates
8.5 The 6 by 6 Member Stiffness Matrix in
Global Coordinates
8.6 Assembly of a Structure Stiffness Matrix—
Direct Stiffness Method
Chapter Outline

Shieh-Kung
Huang
8.1 STRUCTURE STIFFNESS MATRIX
240
Chapter 8 Introduction of Matrix Analysis for Beams and Frames
In the direct stiffness method, we determine values of joint displacements for which the restraining
forces vanish. This is done by first applying the joint restraining forces, but with the sign reversed, and
then solving a set of equilibrium equations that relate forces and displacements at the joints. In matrix
form we have
where F is the column matrix or vector of forces (including moments) in the fictitious restraints but with the
sign reversed,  is the column vector of joint displacements selected as degrees of freedom, and K is the
structure stiffness matrix.
The term degree of freedom (DOF) refers to the independent joint displacement components that are
used in the solution of a particular problem by the direct stiffness method. The number of degrees of
freedom may equal the number of all possible joint displacement components (e.g., three times the
number of free joints in planar frames) or may be smaller if simplifying assumptions (such as neglecting
axial deformations of members) are introduced. In all cases, the number of degrees of freedom and the
degree of kinematic indeterminacy are identical.
=
F KΔ
Member displacement in
Global Coordinate System, 
Member displacement matrix
in Local Coordinate System, 

Shieh-Kung
Huang
8.2 THE 2 BY 2 ROTATIONALSTIFFNESS MATRIX FORA
241
In this section we derive the member stiffness matrix for an individual flexural element using only joint
rotations as degrees of freedom. The 2 × 2 matrix that relates moments and rotations at the ends of the
member is important because it can be used directly in the solution of many practical problems, such as
continuous beams and braced frames where joint translations are prevented.
Since no loads are applied along the member’s axis and no chord rotation  occurs (both  and the
FEM equal zero), the end moments can be expressed as
FLEXURAL MEMBER
2 1
2
1 2
2 1
2
'
1 2
i i
j j
M EI
M L
EI
L


   
 
=
   
 
 
   
 
 =  
 
k

Shieh-Kung
Huang
8.3 THE 4 BY 4 MEMBER STIFFNESS MATRIX IN LOCAL
242
We now derive the member stiffness matrix for a flexural element considering both joint rotations and
transverse joint displacements as degrees of freedom; the axial deformation of the member is still ignored.
With the resulting 4 × 4 matrix we can extend the application of the direct stiffness method to the solution
of structures with joints that both translate and rotate as a result of applied loading.
COORDINATES

Shieh-Kung
Huang
243
We can write these equations in matrix notation as
where the 4 × 4 matrix together with the multiplier 2EI/L is the 4 × 4
member stiffness matrix k′.
COORDINATES
2 2
2 2
3 3
2 1
3 3
1 2
2
3 3 6 6
3 3 6 6
i i
j j
i i
j j
L L
M
M EI L L
V L
L L L L
V
L L L L


 
−
 
 
   
 
−
   
 
   
=  
   

 
−
   

 
   
 
− − −
 
 
2 2
2 2
3 3
2 1
3 3
1 2
2
'
3 3 6 6
3 3 6 6
L L
EI L L
L
L L L L
L L L L
 
−
 
 
 
−
 
=  
 
−
 
 
− − −
 
 
k

Shieh-Kung
Huang
244
In some structures, such as beams and frames treated in the previous sections of this chapter, often
the axial deformations have a negligible effect, and the analysis can be carried out considering bending
deformations only. When it is necessary to include both deformation components, in this section we derive
a member stiffness matrix in local coordinates that will allow us to consider both axial and bending effects
simultaneously.
COORDINATES
2 2
2 2
2 2 3 3
2 2 3 3
4 2 6 6
0 0
2 4 6 6
0 0
6 6 12 12
0 0
'
6 6 12 12
0 0
0 0 0 0
0 0 0 0
EI EI EI EI
L L L L
EI EI EI EI
L L L L
EI EI EI EI
L L L L
EI EI EI EI
L L L L
AE AE
L L
AE AE
L L
 
−
 
 
 
−
 
 
 
−
 
=
 
− − −
 
 
 
−
 
 
 
−
 
 
k

Shieh-Kung
Huang
8.5 THE 6 BY 6 MEMBER STIFFNESS MATRIX IN GLOBAL
245
For convenience, the equation for the transformation of coordinates, originally denoted in Section 7.2,
is repeated below as
where k′ is the member stiffness matrix in local coordinates, k is the member stiffness matrix in global
coordinates, and T is the transformation matrix. The T matrix is formed from the geometric relationships
that exist between the local and the global coordinates. In matrix form
where  and  are the vectors of local and global joint displacements, respectively.
COORDINATES
'
=
k Tk T
=
δ TΔ
0 0 1 0 0 0
0 0 0 0 0 1
0 0 0 0
0 0 0 0
0 0 0 0
0 0 0 0
ix
i
iy
j
i
i
jx
j
jy
i
j
i
s c
s c
c s
c s







 
   
 
    
 
   
 
   

=  
    
  
   
 
    
−
 
   
−  
 
   

Shieh-Kung
Huang
8.6ASSEMBLY OFASTRUCTURE STIFFNESS MATRIX—
246
The final procedure of direct stiffness method
DIRECT STIFFNESS METHOD
Local Coordinate System, k′
Global Coordinate System, k
Member displacement in
Global Coordinate System, 
Member displacement matrix
in Local Coordinate System, 
'
=
k Tk T =
δ TΔ
=
F KΔ
1
−
=
Δ K F

Shieh-Kung
Huang
247
Thanks for your attention!
See you next semester!
Of course, don’t forget the final exam!

Structural Theory II (Part 2/2)

Recommended

Recommended

More Related Content

What's hot

What's hot (20)

Similar to Structural Theory II (Part 2/2)

Similar to Structural Theory II (Part 2/2) (20)

More from National Chung Hsing University

More from National Chung Hsing University (11)

Recently uploaded

Recently uploaded (20)

Structural Theory II (Part 2/2)