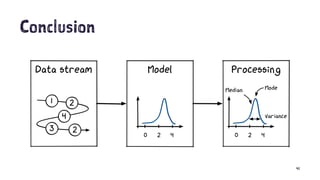
The document discusses a fast and lightweight library for statistical modeling in Scala, addressing issues with traditional Kernel Density Estimation (KDE) methods that require prior knowledge of the dataset. It outlines various functions related to probability and histograms while introducing an adaptive histogram sketch solution. The document also includes examples of random sampling and probability distribution transformations, and concludes with references for further reading.

1. !
Fast and Simple
Statistics with Scala
@xxxnell
1

2. 2

3. 3

4. 4

5. 5

6. 6

7. 7

8. 8

9. 9

10. 10

11. Problems of KDE
4 Slow: or more
4 Large memory consumption:
4 Require a prior knowledge of dataset
11

12. animation link 12

13. 'Adaptive histogram (Sketch)' solves
the problems:
4 Fast:
4 Lightweight:
4 Does NOT require a prior knowledge of dataset
13

14. 14

15. animation link 15

16. animation link 16

17. animation link 17

18. animation link 18

19. Category of probability distributions
19

20. Functions of Dist (simply D)
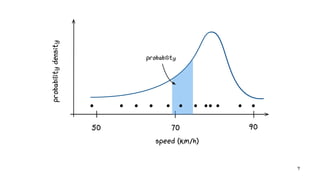
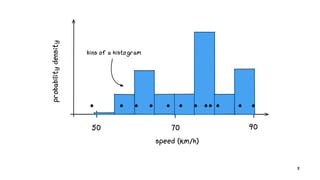
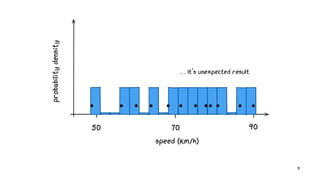
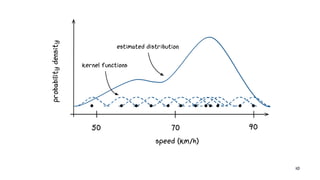
def probability[A](dist: D[A], start: A, end: A): Double
20

21. Functions of Histogram (simply H)
def probability[A](hist: H[A], start: A, end: A): Double
def update[A](hist: H[A], as: List[A]): H[A]
21

22. Functions of Sketch (simply S)
def probability[A](sketch: S[A], start: A, end: A): Double
def update[A](sketch: S[A], as: List[A]): H[A]
def narrowUpdate[A](sketch: S[A], as: List[A]): S[A]
def deepUpdate[A](sketch: S[A], as: List[A]): S[A]
22

23. Functions of Sketch (simply S)
def probability[A](sketch: S[A], start: A, end: A): Double
def narrowUpdate[A](sketch: S[A], as: List[A]): S[A]
def deepUpdate[A](sketch: S[A], as: List[A]): S[A]
23

24. import flip.implicits._
// get 100 random variables from standard normal distribution
val underlying0 = NumericDist.normal(0.0, 1.0)
val (underlying1, samples) = underlying0.samples(100)
// update samples to sketch
val sketch0 = Sketch.empty[Double]
val sketch1 = samples.foldLeft(sketch0) {
case (sketch, sample) ⇒ sketch.update(sample)
}
// get probability for interval [0.0, 1.0]
println("result: " + sketch1.probability(0.0, 1.0))
println("expected: " + underlying1.probability(0.0, 1.0))
24

25. import flip.implicits._
// get 100 random variables from standard normal distribution
val underlying0 = NumericDist.normal(0.0, 1.0)
val (underlying1, samples) = underlying0.samples(100)
// update samples to sketch
val sketch0 = Sketch.empty[Double]
val sketch1 = samples.foldLeft(sketch0) {
case (sketch, sample) ⇒ sketch.update(sample)
}
// get probability for interval [0.0, 1.0]
println("result: " + sketch1.probability(0.0, 1.0))
println("expected: " + underlying1.probability(0.0, 1.0))
25

26. import flip.implicits._
// get 100 random variables from standard normal distribution
val underlying0 = NumericDist.normal(0.0, 1.0)
val (underlying1, samples) = underlying0.samples(100)
// update samples to sketch
val sketch0 = Sketch.empty[Double]
val sketch1 = samples.foldLeft(sketch0) {
case (sketch, sample) ⇒ sketch.update(sample)
}
// get probability for interval [0.0, 1.0]
println("result: " + sketch1.probability(0.0, 1.0))
println("expected: " + underlying1.probability(0.0, 1.0))
26

27. import flip.implicits._
// get 100 random variables from standard normal distribution
val underlying0 = NumericDist.normal(0.0, 1.0)
val (underlying1, samples) = underlying0.samples(100)
// update samples to sketch
val sketch0 = Sketch.empty[Double]
val sketch1 = samples.foldLeft(sketch0) {
case (sketch, sample) ⇒ sketch.update(sample)
}
// get probability for interval [0.0, 1.0]
println("result: " + sketch1.probability(0.0, 1.0))
println("expected: " + underlying1.probability(0.0, 1.0))
27

28. // probability for interval [0.0, 1.0]
sketch.probability(0.0, 1.0)
// probability density at 0.0
sketch.pdf(0.0)
// median
sketch.median
// 100 random samples
sketch.samples(100)
28

29. Rolling one die
29

30. Rolling two dice
30

31. Rolling two dice
for {
n1 ← diceDist
n2 ← diceDist
} yield n1 + n2
31

32. Probability distribution is monad
// premises
def pure[A](a: A): Dist[A]
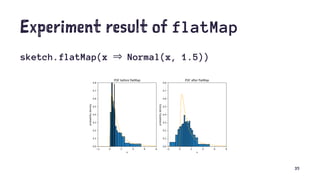
def flatMap[A, B](f: Dist[A], g: A ⇒ Dist[B]): Dist[B]
// proposition
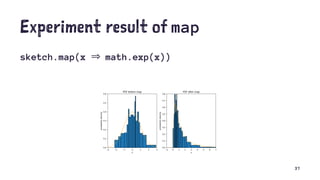
def map[A](f: Dist[A], g: A ⇒ B): Dist[B]
= flatMap(f, (a: A) ⇒ pure(g(a)))
32

33. pure
def pure[A](a: A): Dist[A]
33

34. flatMap
def flatMap[A, B](f: Dist[A], g: A ⇒ Dist[B]): Dist[B]
34

35. Experiment result of flatMap
sketch.flatMap(x ⇒ Normal(x, 1.5))
35

36. map is domain transformation
// translation transformation
sketch.map(x ⇒ x + 1)
// scaling transformation
sketch.map(x ⇒ x * 2)
// reflection transformation
sketch.map(x ⇒ x * -1)
36

37. Experiment result of map
sketch.map(x ⇒ math.exp(x))
37

38. Average speed for three different speed
models
for {
speedA ← speedSketchA
speedB ← speedSketchB
speedC ← speedSketchC
} yield (speedA + speedB + speedC) / 3
38

39. Average height for male and female
for {
gender ← genderDist
height ← gender match {
case Male ⇒ maleHeightDist
case Female ⇒ femaleHeightDist
}
} yield height
39

40. !
Flip: Fast, Lightweight library for
Information and Probability
4 Most fast and lightweight
4 Pure-functional
4 Unique and high-level open source
4 GitHub: https://github.com/xxxnell/flip
40

41. Conclusion
41

42. Further Readings
4 Kernel Density Estimation in Spark
4 A frequentist approach to probability
4 Probability Distribution Monad (code)
4 Foundations of the Giry Monad
4 Platform for statistical modeling
4 A library for probabilistic modeling on TF
42