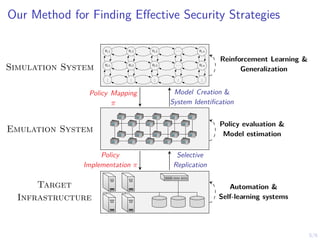
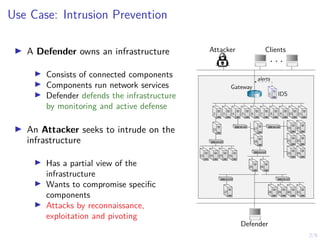
1) The document discusses formulating intrusion prevention as an optimal stopping problem where a defender must monitor an infrastructure over discrete time steps to detect an intrusion by an attacker. 2) If an intrusion is detected, the defender can take defensive actions to stop the intrusion at various time steps, with the goal of stopping intrusions optimally based on observations. 3) The document proposes modeling this problem as a partially observable Markov decision process (POMDP) and using reinforcement learning techniques like simulation and policy evaluation to develop automated security prevention policies that can optimally stop intrusions.

1. 1/6
Intrusion Prevention Through Optimal Stopping
Digital Futures Machine Learning Day
Kim Hammar & Rolf Stadler
kimham@kth.se & stadler@kth.se
Division of Network and Systems Engineering
KTH Royal Institute of Technology
Jan 17, 2022

2. 2/6
Use Case: Intrusion Prevention
I A Defender owns an infrastructure
I Consists of connected components
I Components run network services
I Defender defends the infrastructure
by monitoring and active defense
I An Attacker seeks to intrude on the
infrastructure
I Has a partial view of the
infrastructure
I Wants to compromise specific
components
I Attacks by reconnaissance,
exploitation and pivoting
Attacker Clients
. . .
Defender
1 IDS
1
alerts
Gateway
7 8 9 10 11
6
5
4
3
2
12
13 14 15 16
17
18
19
21
23
20
22
24
25 26
27 28 29 30 31

3. 3/6
Use Case: Intrusion Prevention
I A Defender owns an infrastructure
I Consists of connected components
I Components run network services
I Defender defends the infrastructure
by monitoring and active defense
I An Attacker seeks to intrude on the
infrastructure
I Has a partial view of the
infrastructure
I Wants to compromise specific
components
I Attacks by reconnaissance,
exploitation and pivoting
Attacker Clients
. . .
Defender
1 IDS
1
alerts
Gateway
7 8 9 10 11
6
5
4
3
2
12
13 14 15 16
17
18
19
21
23
20
22
24
25 26
27 28 29 30 31
We formulate this use case as an Optimal Stopping problem

4. 4/6
Formulating Intrusion Prevention as a Stopping Problem
Intrusion event
time-step t = 1 Intrusion ongoing
t
t = T
Episode
Attacker Clients
. . .
Defender
1 IDS
1
alerts
Gateway
7 8 9 10 11
6
5
4
3
2
12
13 14 15 16
17
18
19
21
23
20
22
24
25 26
27 28 29 30 31
I Intrusion Prevention as Optimal Stopping Problem:
I The system evolves in discrete time-steps.
I Defender observes the infrastructure (IDS, log files, etc.).
I An intrusion occurs at an unknown time.
I The defender can make L stops.
I Each stop is associated with a defensive action
I The final stop shuts down the infrastructure.
I Based on the observations, when is it optimal to stop?
I We formalize this problem with a POMDP

5. 4/6
Threshold Properties of the Optimal Defender Policy
b(1)
0 1
belief space B = [0, 1]
S 1
S 2
.
.
.
S L
α∗
1
α∗
2
α∗
L
. . .

6. 5/6
Our Method for Finding Effective Security Strategies
s1,1 s1,2 s1,3 . . . s1,n
s2,1 s2,2 s2,3 . . . s2,n
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
Emulation System
Target
Infrastructure
Model Creation &
System Identification
Policy Mapping
π
Selective
Replication
Policy
Implementation π
Simulation System
Reinforcement Learning &
Generalization
Policy evaluation &
Model estimation
Automation &
Self-learning systems

7. 6/6
Conclusions
I We develop a method to learn automated security prevention
policies
1. emulation system;
2. system identification;
3. simulation system;
4. reinforcement learning
5. domain randomization and generalization.
I We apply the method to an intrusion prevention use case.
I We formulate intrusion prevention as a multiple stopping
problem
I We model it as a POMDP
I We apply the stopping theory to establish structural results of
the optimal policy