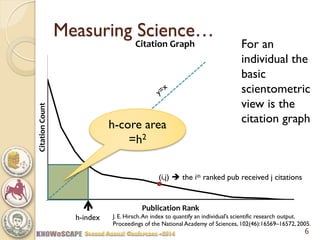
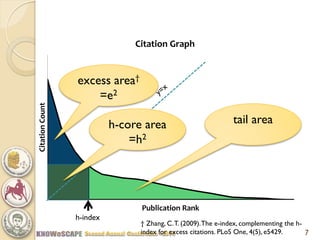
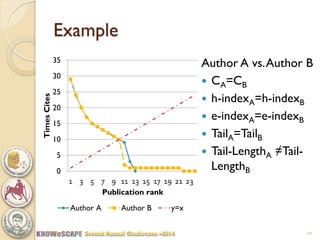
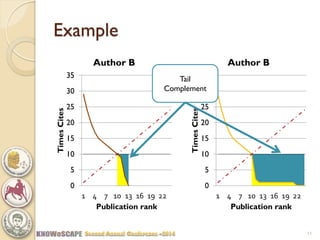
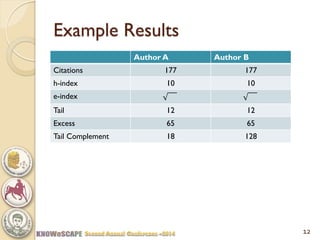
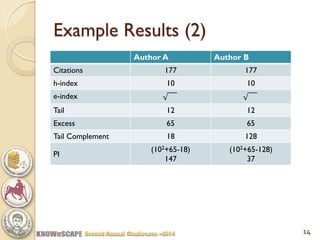
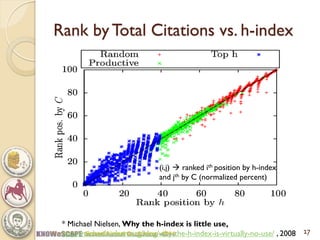
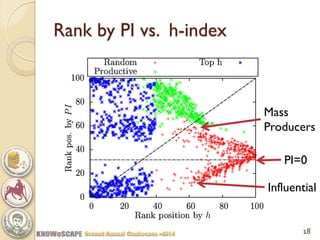
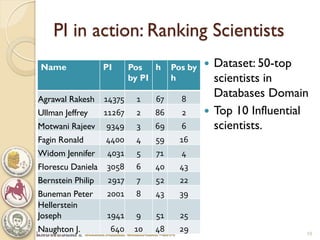
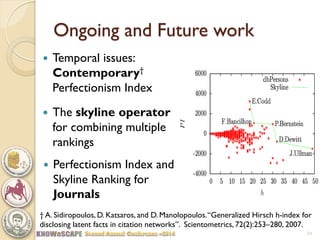
The document discusses the concept of the Perfectionism Index (PI), which quantifies scientific impact based on publication metrics like citations and h-index, distinguishing between influential scientists and mass producers. It proposes that strict promotion based on scientific merit could transform scientific careers, and outlines how the PI can categorize scientists based on their research output. The key takeaway is that a PI above zero indicates an influential scientist, while below zero indicates a mass producer.

1. Perfectionism Index: Identification of Influential Scientists vs. Mass Producers
1

2. 2
What is “Science”?
“A branch of study in which facts are observed and classified, and, usually, quantitative laws are formulated and verified: involves the application of mathematical reasoning and data analysis to natural phenomena”
Dictionary of Scientific and Technical Terms
Science is developed every second, everywhere !
Are all these science products of great importance?

3. What if we could measure “Science” itself
Careers in science are not only scientific; they also depend on:
◦luck
◦social connections
◦the ability to impress influential people and referees
◦the foresight to join the right lab at the right time
◦the foresight to associate oneself with prestigious people and prestigious projects
Such systems waste scientific talent and produce resentment
3

4. What if we could measure “Science” itself
Promotion strictly according to scientific merit would revolutionize scientific career
Scientific production: the basis for any measurement of scientific merit
◦Scientific production consists of:
published articles (in premium quality venues†)
and their impact (article citations)
4
† A Sidiropoulos, Y Manolopoulos. “Generalized comparison of graph-based ranking algorithms for publications and authors”, Journal of Systems and Software 79 (12), 1679-1700, 2006

5. 5
Measuring “Science”…
Can we quantitatively measure the output of science?
YES! we can…
•Numerical indices (based on citation analysis) for quantification of published research output are being increasingly used by:
•employers for hiring personnel
•promotion panels: promotions, tenure
•funding agencies: “Funding does not regenerate funding. But reputation does.”

6. Measuring Science…
Citation Count
Publication Rank
Citation Graph
h-index
h-core area =h2
(i,j)  the ith ranked pub received j citations
For an individual the basic scientometric view is the citation graph
J. E. Hirsch. An index to quantify an individual’s scientific research output. Proceedings of the National Academy of Sciences, 102(46):16569–16572, 2005.
6

7. Citation Count
Publication Rank
Citation Graph
h-index
h-core area =h2
excess area† =e2
tail area
7
† Zhang, C. T. (2009). The e-index, complementing the h- index for excess citations. PLoS One, 4(5), e5429.

8. The Basic Citation Graph Areas
Overall area: The total number of citations
h-index: Denotes the distance of the plot line from the point (0,0).
e-index: denotes the “big hits”
Tail: denotes the quality of remaining publications
8

9. The Tail of the Citation Graph
Tail:
◦short and wide tail denotes that
there are no many publications in the tail
These pubs got a relatively significant number of citations
◦long and slim tail means that
The researcher is productive
The “products” did not have enough acceptance by the research community
 massive productivity with not enough acceptance
Conclusion: the tail carries important information
9

10. Example
0
5
10
15
20
25
30
35
1
3
5
7
9
11
13
15
17
19
21
23
Times Cites
Publication rank
Author A
Author B
y=x
Author A vs. Author B
CA=CB
h-indexA=h-indexB
e-indexA=e-indexB
TailA=TailB
Tail-LengthA ≠Tail- LengthB
10

11. Example
0
5
10
15
20
25
30
35
1
4
7
10
13
16
19
22
Times Cites
Publication rank
Author B
0
5
10
15
20
25
30
35
1
4
7
10
13
16
19
22
Times Cites
Publication rank
Author B
Tail Complement
11

12. Example Results
Author A
Author B
Citations
177
177
h-index
10
10
e-index
Tail
12
12
Excess
65
65
Tail Complement
18
128
12

13. The Perfectionism Index (PI)
PI = κ ∗ h2 + λ ∗ CE − ν ∗ CTC
h2 : the h-core area
CE : the excess area
CTC: the tail complement area
κ = λ = ν = 1 (or any number)
◦if κ = ν = 1 and λ=2 we consider that the excess area is more important.
◦κ = λ = ν = 1 give a straightforward geometrical approach.
13

14. Example Results (2)
Author A
Author B
Citations
177
177
h-index
10
10
e-index
Tail
12
12
Excess
65
65
Tail Complement
18
128
PI
(102+65-18) 147
(102+65-128) 37
14

15. What is the Perfectionism Index ?
Can be used for Classifying scientists:
◦Truly laconic and Influential*: Most of their work has impact
◦Mass producers* : Long List of publications with relatively low impact
The value of zero for PI is a key value:
◦PI>0  The scientist is influential
◦PI<0  The scientist is mass producer
15
* The terms where proposed by “Cole, S., & Cole, J. (1967). Scientific Output and Recognition: A study in the Operation of the Reward System in Science. American Sociological Review, 32(3), 377–390.”.

16. Experiments
Dataset based on MS Academic Search API
3 datasets:
◦Random: 500 authors from CS
with P≥10 and C≥1
◦Productive: 500 top authors from CS based on number of publications
found P≥354
◦Top h: 500 top author from CS based on h-index
found P≥92
16

17. Rank by Total Citations vs. h-index
(i,j)  ranked ith position by h-index and jth by C (normalized percent)
17
* Michael Nielsen, Why the h-index is little use, http://michaelnielsen.org/blog/why-the-h-index-is-virtually-no-use/ , 2008

18. Rank by PI vs. h-index
PI=0
18
Influential
Mass Producers

19. PI in action: Ranking Scientists
Name
PI
Pos by PI
h
Pos by h
Agrawal Rakesh
14375
1
67
8
Ullman Jeffrey
11267
2
86
2
Motwani Rajeev
9349
3
69
6
Fagin Ronald
4400
4
59
16
Widom Jennifer
4031
5
71
4
Florescu Daniela
3058
6
40
43
Bernstein Philip
2917
7
52
22
Buneman Peter
2001
8
43
39
Hellerstein Joseph
1941
9
51
25
Naughton J.
640
10
48
29
19
Dataset: 50-top scientists in Databases Domain
Top 10 Influential scientists.

20. Conclusion
We introduced PI to provide quantifiable definitions of earlier qualitative classification schemes for the output of scientists
PI is uncorrelated with any other known metric.
the value of zero for PI is a key value:
◦PI>0  The scientist is influential
◦PI<0  The scientist is mass producer
More Results can be found at:
◦http://arxiv.org/abs/1409.6099
20

21. Ongoing and Future work
Perfectionism Index and Skyline Ranking for Journals
21
† A. Sidiropoulos, D. Katsaros, and D. Manolopoulos. “Generalized Hirsch h-index for disclosing latent facts in citation networks”. Scientometrics, 72(2):253–280, 2007.
Temporal issues: Contemporary† Perfectionism Index
The skyline operator for combining multiple rankings

22. Thank you for your attention
Questions ?
Contact & Info:
◦Antonis Sidiropoulos: https://sites.google.com/site/asidirop/
◦Dimitris Katsaros: http://inf-server.inf.uth.gr/~dkatsar/
◦Yannis Manolopoulos: http://delab.csd.auth.gr/~manolopo/
22