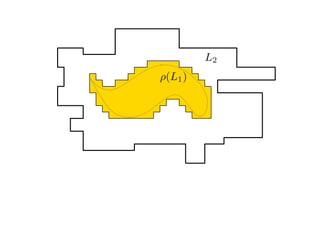
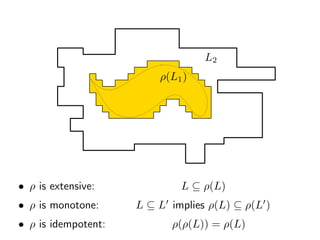
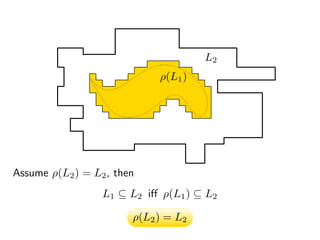
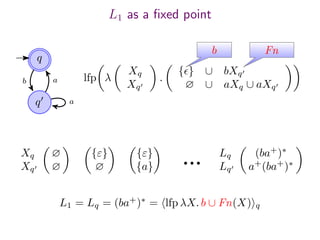
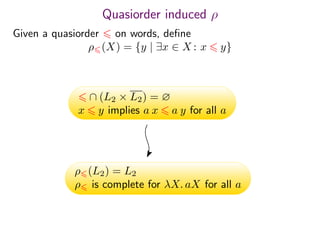
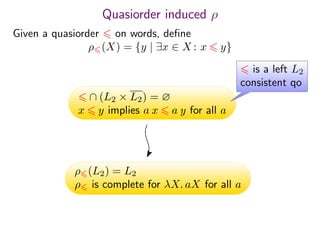
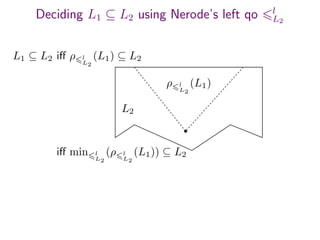
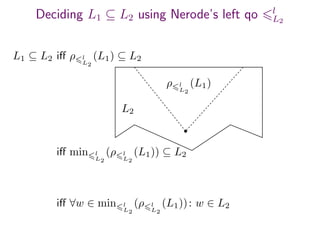
The document summarizes research on deciding language inclusion problems using quasiorders. It introduces the concept of a quasiorder ρ induced by a language L2 that is extensive, monotone, and idempotent. Language inclusion L1 ⊆ L2 can be decided by checking if ρ(L1) is contained within L2. The Nerode left quasiorder relative to L2 is presented, which allows reducing the problem to checking membership of finitely many words. An algorithm is provided that computes the minimal elements of ρ applied to L1 using antichains. The approach is generalized to state-based quasiorders defined using automata for L2.

1. Deciding language inclusion problems
using quasiorders
Pierre Ganty IMDEA Software Institute
joint work with Pedro Valero (IMDEA) and Francesco Ranzato (Uni. Padova)

2. L1

3. L1
L2

4. L1
L2

5. L2
ρ(L1)

6. L2
ρ(L1)
• ρ is extensive: L ⊆ ρ(L)
• ρ is monotone: L ⊆ L implies ρ(L) ⊆ ρ(L )
• ρ is idempotent: ρ(ρ(L)) = ρ(L)

7. L2
ρ(L1)
L1 ⊆ L2 iff ρ(L1) ⊆ L2
Assume ρ(L2) = L2, then
ρ(L2) = L2

8. L1 as a fixed point
q
q
b a
a
lfp λ
Xq
Xq
.
{ } ∪ bXq
∅ ∪ aXq ∪ aXq

9. L1 as a fixed point
q
q
b a
a
lfp λ
Xq
Xq
.
{ } ∪ bXq
∅ ∪ aXq ∪ aXq
Xq ∅
Xq ∅

10. L1 as a fixed point
q
q
b a
a
lfp λ
Xq
Xq
.
{ } ∪ bXq
∅ ∪ aXq ∪ aXq
Xq ∅
Xq ∅
{ε}
∅

11. L1 as a fixed point
q
q
b a
a
lfp λ
Xq
Xq
.
{ } ∪ bXq
∅ ∪ aXq ∪ aXq
Xq ∅
Xq ∅
{ε}
∅
{ε}
{a}

12. L1 as a fixed point
q
q
b a
a
lfp λ
Xq
Xq
.
{ } ∪ bXq
∅ ∪ aXq ∪ aXq
Lq (ba+
)∗
Lq a+
(ba+
)∗
Xq ∅
Xq ∅
{ε}
∅
{ε}
{a}

13. L1 as a fixed point
q
q
b a
a
lfp λ
Xq
Xq
.
{ } ∪ bXq
∅ ∪ aXq ∪ aXq
L1 = Lq = (ba+
)∗
= lfp λX. b ∪ Fn(X) q
Lq (ba+
)∗
Lq a+
(ba+
)∗
Xq ∅
Xq ∅
{ε}
∅
{ε}
{a}

14. L1 as a fixed point
q
q
b a
a
lfp λ
Xq
Xq
.
{ } ∪ bXq
∅ ∪ aXq ∪ aXq
L1 = Lq = (ba+
)∗
= lfp λX. b ∪ Fn(X) q
Lq (ba+
)∗
Lq a+
(ba+
)∗
Xq ∅
Xq ∅
{ε}
∅
{ε}
{a}
b Fn

15. ρ(L1) = ρ lfp λX. b ∪ Fn(X)
ρ(L1)
if ρ is complete for Fn (i.e. ρ Fn ρ = ρ Fn) then
ρ(L1) = lfp λX. ρ b ∪ Fn(X)

16. ρ(L1) = ρ lfp λX. b ∪ Fn(X)
ρ(L1)
if ρ is complete for Fn (i.e. ρ Fn ρ = ρ Fn) then
ρ(L1) = lfp λX. ρ b ∪ Fn(X)
ρ is complete for Fn

17. Wanted
ρ(L2) = L2
ρ is complete for Fn

18. Quasiorder induced ρ
Given a quasiorder on words, define
ρ (X) = {y | ∃x ∈ X : x y}

19. Quasiorder induced ρ
Given a quasiorder on words, define
ρ (X) = {y | ∃x ∈ X : x y}
∩ (L2 × L2) = ∅
x y implies a x a y for all a

20. Quasiorder induced ρ
Given a quasiorder on words, define
ρ (X) = {y | ∃x ∈ X : x y}
∩ (L2 × L2) = ∅
x y implies a x a y for all a
ρ (L2) = L2
ρ is complete for λX. aX for all a

21. Quasiorder induced ρ
Given a quasiorder on words, define
ρ (X) = {y | ∃x ∈ X : x y}
∩ (L2 × L2) = ∅
x y implies a x a y for all a
ρ (L2) = L2
ρ is complete for λX. aX for all a
is a left L2
consistent qo

22. Example of quasiorder
Nerode left quasiorder relative to L2 [Varricchio,deLuca’94]
x l
L2
y ⇔ L2 x−1
⊆ L2 y−1

23. Example of quasiorder
Nerode left quasiorder relative to L2 [Varricchio,deLuca’94]
x l
L2
y ⇔ L2 x−1
⊆ L2 y−1
Lx−1
= {w | wx ∈ L}

24. Example of quasiorder
Nerode left quasiorder relative to L2 [Varricchio,deLuca’94]
x l
L2
y ⇔ L2 x−1
⊆ L2 y−1
l
L2
is left L2 consistent

25. Example of quasiorder
Nerode left quasiorder relative to L2 [Varricchio,deLuca’94]
x l
L2
y ⇔ L2 x−1
⊆ L2 y−1
l
L2
is left L2 consistent
l
L2
is a well-quasi order if L2 is regular

26. Example of quasiorder
Nerode left quasiorder relative to L2 [Varricchio,deLuca’94]
x l
L2
y ⇔ L2 x−1
⊆ L2 y−1
l
L2
is left L2 consistent
l
L2
is a well-quasi order if L2 is regular
l
L2
is decidable if L2 is regular

27. Deciding L1 ⊆ L2 using Nerode’s left qo l
L2
L1 ⊆ L2 iff ρ l
L2
(L1) ⊆ L2

28. Deciding L1 ⊆ L2 using Nerode’s left qo l
L2
L1 ⊆ L2 iff ρ l
L2
(L1) ⊆ L2
ρ l
L2
(L1)

29. Deciding L1 ⊆ L2 using Nerode’s left qo l
L2
L1 ⊆ L2 iff ρ l
L2
(L1) ⊆ L2
ρ l
L2
(L1)
L2

30. Deciding L1 ⊆ L2 using Nerode’s left qo l
L2
L1 ⊆ L2 iff ρ l
L2
(L1) ⊆ L2
iff min l
L2
(ρ l
L2
(L1)) ⊆ L2
ρ l
L2
(L1)
L2

31. Deciding L1 ⊆ L2 using Nerode’s left qo l
L2
L1 ⊆ L2 iff ρ l
L2
(L1) ⊆ L2
iff min l
L2
(ρ l
L2
(L1)) ⊆ L2
iff ∀w ∈ min l
L2
(ρ l
L2
(L1)): w ∈ L2
ρ l
L2
(L1)
L2

32. Deciding L1 ⊆ L2 using l
L2
(cont’d)
L1 ⊆ L2 iff ∀w ∈ min l
L2
(ρ l
L2
(L1)): w ∈ L2

33. Deciding L1 ⊆ L2 using l
L2
(cont’d)
L1 ⊆ L2 iff ∀w ∈ min l
L2
(ρ l
L2
(L1)): w ∈ L2
iff ∀w ∈ min l
L2
(lfp λX. ρ l
L2
b ∪ Fn(X) : w ∈ L2

34. Deciding L1 ⊆ L2 using l
L2
(cont’d)
L1 ⊆ L2 iff ∀w ∈ min l
L2
(ρ l
L2
(L1)): w ∈ L2
iff ∀w ∈ min l
L2
(lfp λX. ρ l
L2
b ∪ Fn(X) : w ∈ L2

35. Deciding L1 ⊆ L2 using l
L2
(cont’d)
L1 ⊆ L2 iff ∀w ∈ min l
L2
(ρ l
L2
(L1)): w ∈ L2
iff ∀w ∈ min l
L2
(lfp λX. ρ l
L2
b ∪ Fn(X) : w ∈ L2

36. Deciding L1 ⊆ L2 using l
L2
(cont’d)
L1 ⊆ L2 iff ∀w ∈ min l
L2
(ρ l
L2
(L1)): w ∈ L2
iff ∀w ∈ min l
L2
(lfp λX. ρ l
L2
b ∪ Fn(X) : w ∈ L2

37. Deciding L1 ⊆ L2 using l
L2
(cont’d)
L1 ⊆ L2 iff ∀w ∈ min l
L2
(ρ l
L2
(L1)): w ∈ L2
iff ∀w ∈ min l
L2
(lfp λX. ρ l
L2
b ∪ Fn(X) : w ∈ L2

38. Deciding L1 ⊆ L2 using l
L2
(cont’d)
L1 ⊆ L2 iff ∀w ∈ min l
L2
(ρ l
L2
(L1)): w ∈ L2
iff ∀w ∈ lfp λX. min l
L2
b ∪ Fn(X) : w ∈ L2
iff ∀w ∈ min l
L2
(lfp λX. ρ l
L2
b ∪ Fn(X) : w ∈ L2

39. Deciding L1 ⊆ L2 using l
L2
(cont’d)
L1 ⊆ L2 iff ∀w ∈ min l
L2
(ρ l
L2
(L1)): w ∈ L2
iff ∀w ∈ lfp λX. min l
L2
b ∪ Fn(X) : w ∈ L2
iff ∀w ∈ min l
L2
(lfp λX. ρ l
L2
b ∪ Fn(X) : w ∈ L2

40. Word-based antichain algorithm for L(A) ⊆ L2
Data: FA A = Q, δ, q0
, F
Data: L2 regular
1 Yq q∈Q := ∅;
2 repeat
3 Xq q∈Q := Yq q∈Q;
4 Yq q∈Q := min l
L2
b ∪ Fn( Yq q∈Q) ;
5 until ρ l
L2
( Yq q∈Q) ⊆ ρ l
L2
( Xq q∈Q);
6 forall u ∈ Yq0 do
7 if u /∈ L2 then return false;
8 return true;

41. What else?
Nerode left quasiorder relative to L2 [Varricchio,deLuca’94]
x l
L2
y ⇔ L2 x−1
⊆ L2 y−1

42. What else?
State based quasiorder
Let A2 = Q2, δ2, q0
2, F2 be an automaton for L2
x l
A2
y ⇔ prex(F2) ⊆ prey(F2)
Nerode left quasiorder relative to L2 [Varricchio,deLuca’94]
x l
L2
y ⇔ L2 x−1
⊆ L2 y−1

43. What else?
State based quasiorder
Let A2 = Q2, δ2, q0
2, F2 be an automaton for L2
x l
A2
y ⇔ prex(F2) ⊆ prey(F2)
Nerode left quasiorder relative to L2 [Varricchio,deLuca’94]
x l
L2
y ⇔ L2 x−1
⊆ L2 y−1
1. l
A2
∩ (L2 × L2) = ∅
2. x l
A2
y implies a x l
A2
a y for all a
3. l
A2
is a well-quasiorder
4. l
A2
is decidable

44. What else?
State based quasiorder
Let A2 = Q2, δ2, q0
2, F2 be an automaton for L2
x l
A2
y ⇔ prex(F2) ⊆ prey(F2)
Nerode left quasiorder relative to L2 [Varricchio,deLuca’94]
x l
L2
y ⇔ L2 x−1
⊆ L2 y−1
1. l
A2
∩ (L2 × L2) = ∅
2. x l
A2
y implies a x l
A2
a y for all a
3. l
A2
is a well-quasiorder
4. l
A2
is decidable
l
A2
is left L2 consistent
decidable wqo

45. Word-based antichain algorithm for L(A1) ⊆ L(A2)
Data: FA A1 = Q1, δ1, q0
1, F1
Data: FA A2 = Q2, δ2, q0
2, F2
1 Yq q∈Q1
:= ∅;
2 repeat
3 Xq q∈Q1
:= Yq q∈Q1
;
4 Yq q∈Q1
:= min l
A2
b ∪ Fn( Yq q∈Q1
) ;
5 until ρ l
A2
( Yq q∈Q1
) ⊆ ρ l
A2
( Xq q∈Q1
);
6 forall u ∈ Yq0
1
do
7 if u /∈ L(A2) then return false;
8 return true;

46. Word-based antichain algorithm for L(A1) ⊆ L(A2)
Data: FA A1 = Q1, δ1, q0
1, F1
Data: FA A2 = Q2, δ2, q0
2, F2
1 Yq q∈Q1
:= ∅;
2 repeat
3 Xq q∈Q1
:= Yq q∈Q1
;
4 Yq q∈Q1
:= min l
A2
b ∪ Fn( Yq q∈Q1
) ;
5 until ρ l
A2
( Yq q∈Q1
) ⊆ ρ l
A2
( Xq q∈Q1
);
6 forall u ∈ Yq0
1
do
7 if u /∈ L(A2) then return false;
8 return true;
State based quasiorder
Let A2 = Q2, δ2, q0
2, F2 be an automaton for L2
x l
A2
y ⇔ prex(F2) ⊆ prey(F2)

47. Ditching words altogether
State-based antichain algorithm for L(A1) ⊆ L(A2)
Data: FA A1 = Q1, δ1, q0
1, F1
Data: FA A2 = Q2, δ2, q0
2, F2
1 Yq q∈Q1
:= ∅;
2 repeat
3 Xq q∈Q1
:= Yq q∈Q1
;
4 Yq q∈Q1 := [. . .];
5 until Yq ⊆∀∃
Xq, for all q ∈ Q1;
6 forall s ∈ Yq0
1
do
7 if q0
2 /∈ s then return false;
8 return true;
[. . .] = min⊆∀∃ {preA2
a (s) | ∃a ∈ Σ, q ∈ δ1(q, a), s ∈ Xq } ∪ F2

48. • Same as antichain algo
• Derived from general solution instantiated to l
A2
• Variants of the antichain algorithm as instantiations
• Simulation enhanced qo 2
• Nerode’s qo induce the coarsest qo based abstractions

49. • Same as antichain algo
• Derived from general solution instantiated to l
A2
• Variants of the antichain algorithm as instantiations
• Simulation enhanced qo 2
• Nerode’s qo induce the coarsest qo based abstractions
l
L2
and r
L2
are wqo’s if L2 is regular

50. L2 is a one-counter net trace set
q2
q1
q3a, 1
a, 0
a, −1
b, 1
The right Nerode qo for L2 ( r
L2
) is a wqo but it’s undecidable
u r
O2
v is a right L2 consistent decidable wqo
u r
O2
v iff mu ≤ mv where mu, mv ∈ (N ∪ {⊥})3
L2 = L(O2) is the set of traces
from configuration q2 0

51. Decision procedure for L(A1) ⊆ L(O2) using r
O2
Word-based antichain algorithm for L(A) ⊆ L(O2)
Data: FA A = Q, δ, q0
, F
Data: OCN O2
1 Yq q∈Q := ∅;
2 repeat
3 Xq q∈Q := Yq q∈Q;
4 Yq q∈Q := min r
O2
b ∪ Gn( Yq q∈Q) ;
5 until ρ r
O2
( Yq q∈Q) ⊆ ρ r
O2
( Xq q∈Q);
6 forall u ∈ Yq0 do
7 if u /∈ L2 then return false;
8 return true;

52. So far. . .
L(A1) ⊆ L(A2)
L(A1) ⊆ L(O2)

53. ρ(L1) = ρ lfp λX. b ∪ Fn(X)
= lfp λX. ρ b ∪ Fn(X)
L2
ρ(L1)

54. ρ(L1) = ρ lfp λX. b ∪ Fn(X)
= lfp λX. ρ b ∪ Fn(X)
L2
ρ(L1)
ρ Fn ρ = ρ Fn

55. ρ(L1) = ρ lfp λX. b ∪ Fn(X)
= lfp λX. ρ b ∪ Fn(X)
L2
ρ(L1)
When L1 is regular, ρ is complete for λX. aX for all a
ρ Fn ρ = ρ Fn
lfp λ
Xq
Xq
.
{ } ∪ bXq
∅ ∪ aXq ∪ aXq

56. Quasiorders for the case L(G1) ⊆ L(A2)
FnG1
is more general: from aX, Xa, aXb, XX

57. Quasiorders for the case L(G1) ⊆ L(A2)
FnG1
is more general: from aX, Xa, aXb, XX
ρ(L1) = lfp λX. ρ b ∪ FnG1 (X)
if ρ is complete for λX. aX and λX. Xa for all a

58. Quasiorders for the case L(G1) ⊆ L(A2)
FnG1
is more general: from aX, Xa, aXb, XX
1. ∩ (L2 × L2) = ∅
2. x y implies a x a y and x a y a for all a
ρ(L1) = lfp λX. ρ b ∪ FnG1 (X)
if ρ is complete for λX. aX and λX. Xa for all a

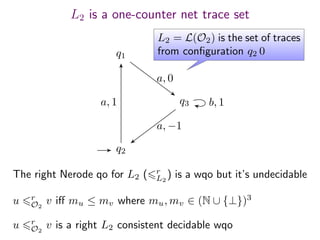
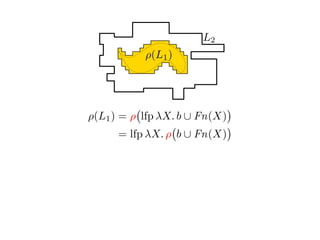
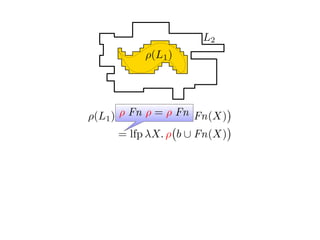
59. Quasiorders for the case L(G1) ⊆ L(A2)
Myhill quasiorder relative to L2 [Varricchio, deLuca’94]
x L2
y ⇔ {(u, v) | u x v∈L2} ⊆ {(u, v) | u y v∈L2}
FnG1
is more general: from aX, Xa, aXb, XX
1. ∩ (L2 × L2) = ∅
2. x y implies a x a y and x a y a for all a
ρ(L1) = lfp λX. ρ b ∪ FnG1 (X)
if ρ is complete for λX. aX and λX. Xa for all a

60. Quasiorders for the case L(G1) ⊆ L(A2)
Myhill quasiorder relative to L2 [Varricchio, deLuca’94]
x L2
y ⇔ {(u, v) | u x v∈L2} ⊆ {(u, v) | u y v∈L2}
State based quasi order [Netys’15]
x A2
y ⇔ {(q, q ) | q
x
q } ⊆ {(q, q ) | q
y
q }
FnG1
is more general: from aX, Xa, aXb, XX
1. ∩ (L2 × L2) = ∅
2. x y implies a x a y and x a y a for all a
ρ(L1) = lfp λX. ρ b ∪ FnG1 (X)
if ρ is complete for λX. aX and λX. Xa for all a

61. Greatest fixpoint based approach
lfp λX. b ∪ Fn(X) ⊆ L2 iff b ⊆ gfp λX. L2 ∩ Fn(X)
∪ becomes ∩
λX. aX becomes λX. a−1
X
ρ Fn ρ = ρ Fn becomes ρ Fn ρ = Fn ρ
gfp λX. ρ(L2 ∩ Fn(X)) stepwise equal gfp λX. L2 ∩ Fn(X)

62. Greatest fixpoint based approach
lfp λX. b ∪ Fn(X) ⊆ L2 iff b ⊆ gfp λX. L2 ∩ Fn(X)
∪ becomes ∩
λX. aX becomes λX. a−1
X
ρ Fn ρ = ρ Fn becomes ρ Fn ρ = Fn ρ
gfp λX. ρ(L2 ∩ Fn(X)) stepwise equal gfp λX. L2 ∩ Fn(X)
Does not terminate in general

63. Greatest fixpoint based approach
lfp λX. b ∪ Fn(X) ⊆ L2 iff b ⊆ gfp λX. L2 ∩ Fn(X)
∪ becomes ∩
λX. aX becomes λX. a−1
X
ρ Fn ρ = ρ Fn becomes ρ Fn ρ = Fn ρ
gfp λX. ρ(L2 ∩ Fn(X)) stepwise equal gfp λX. L2 ∩ Fn(X)
Does not terminate in general
Does always terminate 1

64. Conclusion
Promising framework for language inclusion

65. Conclusion
Promising framework for language inclusion
Extension to trees, ω-languages, timed languages,. . .

66. Conclusion
Promising framework for language inclusion
Extension to trees, ω-languages, timed languages,. . .
Technical Report 1904.01388 on arxiv.org