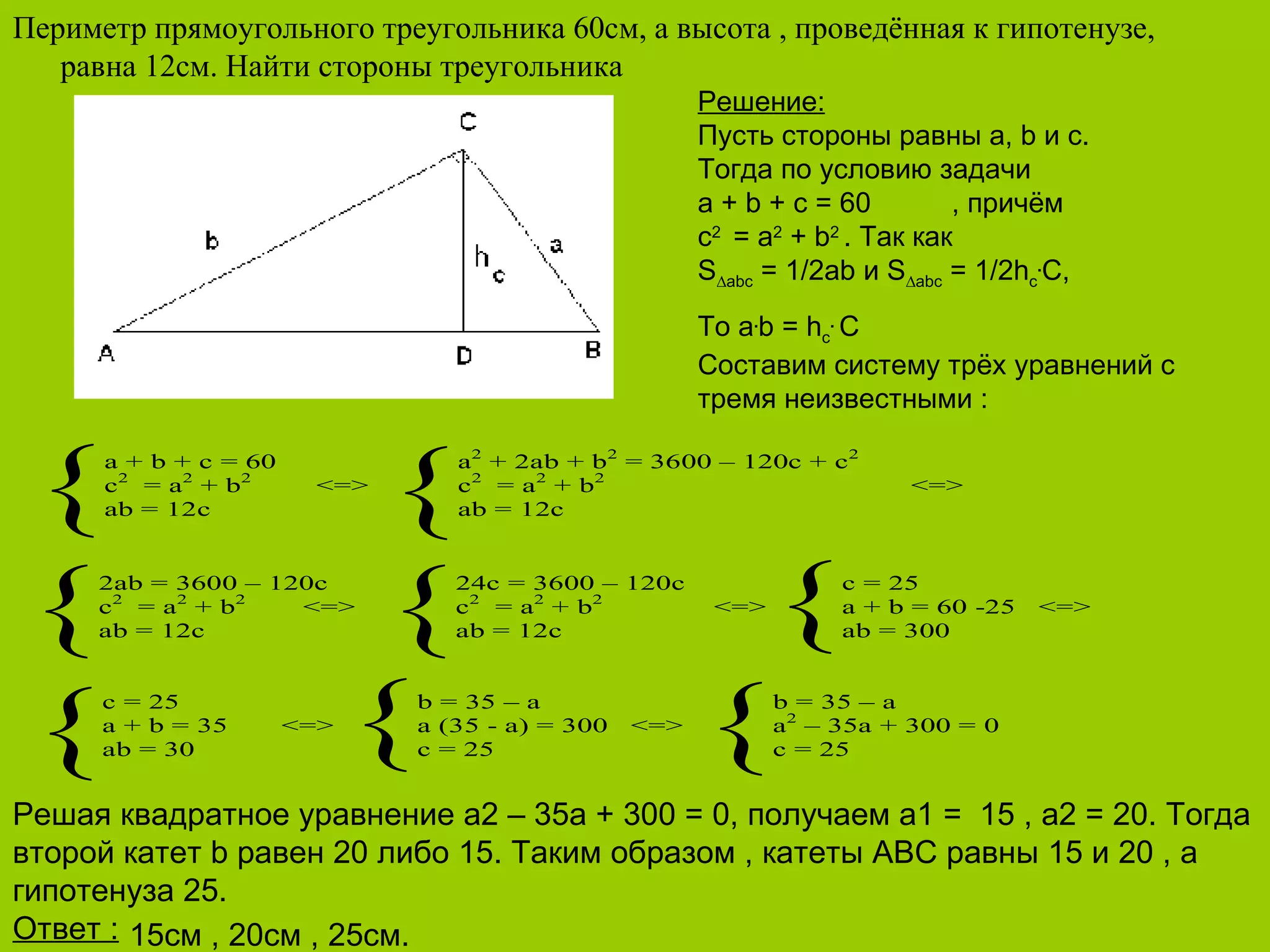
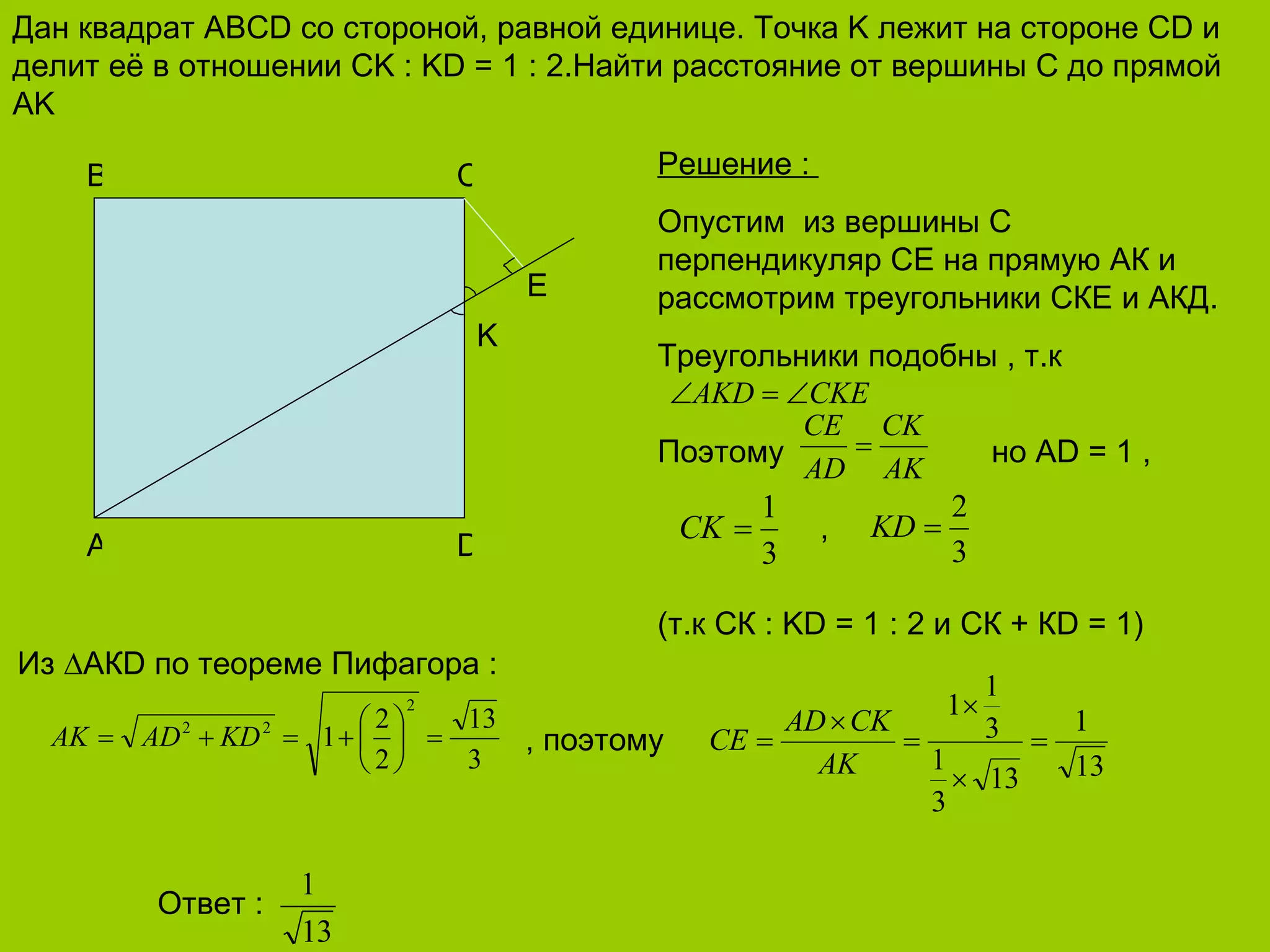
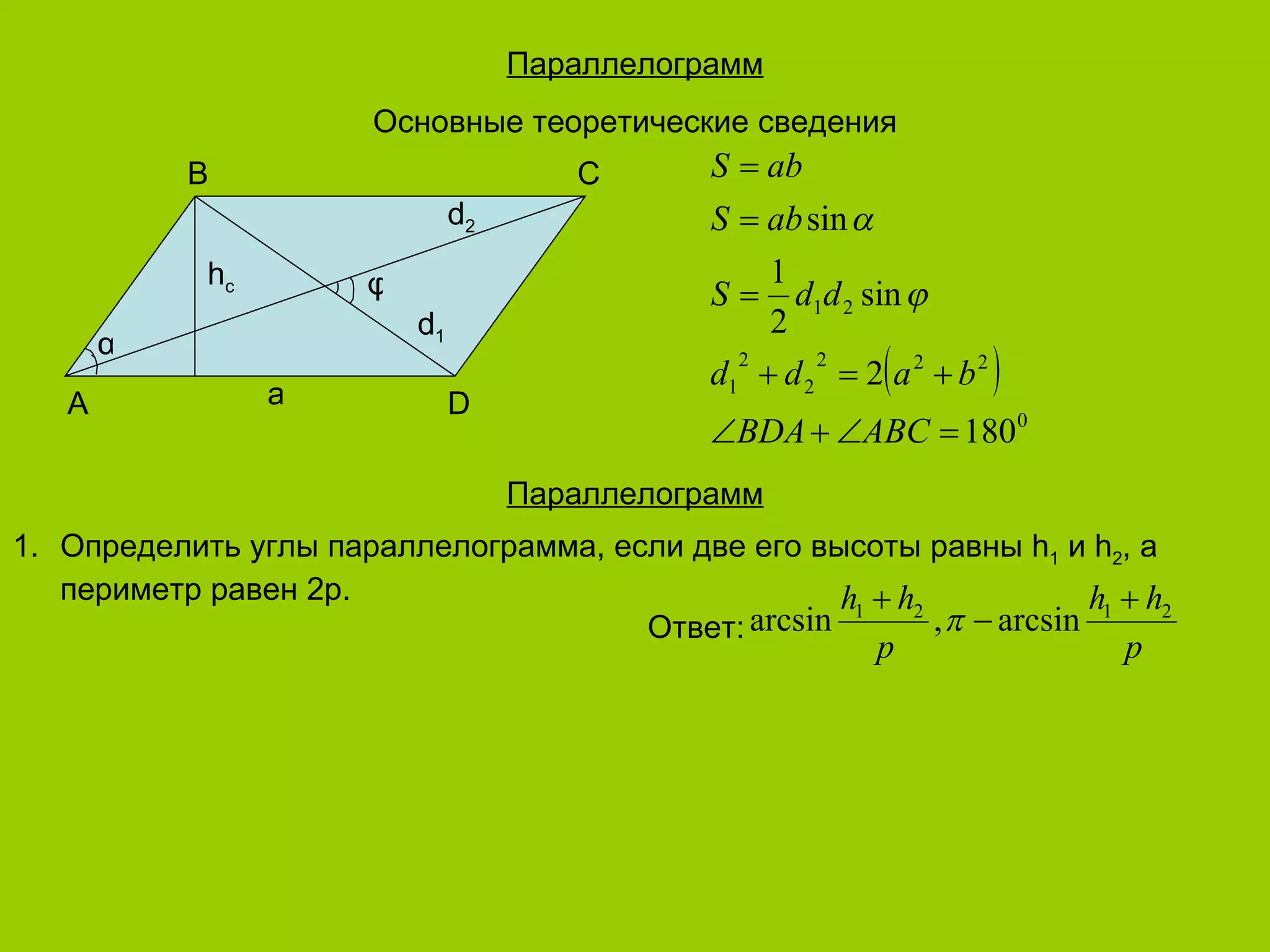
Документ содержит ряд задач по планиметрии, связанных с различными типами треугольников и их свойствами. Приведены примеры находки площадей, сторон и углов треугольников, а также определения радиусов описанных и вписанных окружностей. Каждое решение сопровождается правильными ответами и кратким пояснением методологии решения.

1. Подготовка к государственному экзамену по математике

2. Прямоугольный треугольник Даны проекции катетов а с и b c . Найти площадь треугольника Ответ : 6. Дан квадрат ABCD со стороной, равной единице. Точка K лежит на стороне CD и делит её в отношении CK:KD = 1:2. Найти расстояние от вершины C до прямой AK. Ответ : 5. Полуокружность с диаметром, равным катету прямоугольного треугольника, делит гипотенузу в отношении m:n. Определить углы треугольника. Ответ : 4. Определить острые углы прямоугольного треугольника, стороны которого составляют арифметическую прогрессию. Ответ : 2. Периметр прямоугольного треугольника равен 60 см, а высота, проведённая к гипотенузе, равна 12 см. Найти стороны треугольника. Ответ : Планиметрия Решение задач 3. В прямоугольном треугольнике гипотенуза равна с, а биссектриса одного из острых углов равна . Найти катеты. Ответ :

3. Равнобедренный, равносторонний, произвольный треугольник В равнобедренном треугольнике величина угла при вершине равна α , а площадь равна S. Найти длину основания треугольника. Ответ : 13. Найти углы треугольника, в котором высота и медиана, проведённые из одной вершины, делят угол при этой вершине на равные части. Ответ : 12. Длины сторон AC и AB треугольника ABC равны b и с,угол А вдвое больше угла B. Найти длину стороны BC. Ответ : 10. Высота треугольника равна 6 и делит угол в отношении 2 : 1, а основание треугольника – на отрезки, меньший из которых равен 3. Найти стороны треугольника. Ответ : 9. Сторона треугольника имеет длину С, прилежащие к ней углы равны α и β . Найти площадь треугольника. Ответ : 25 8. В равнобедренном треугольнике ABC основание AB равно 30, а высота AD равна 24. Найти длину боковой стороны. Ответ : 11. В треугольнике ABC сторона AB равна 2, медиана BD равна 1, а угол равен 30 0 . Найти площадь треугольника ABC. Ответ : 10 ;11

4. Вписанные и описанные треугольники Величины углов треугольника относятся как 2:3:7 . Длина наименьшей стороны равна a . Найдите радиус окружности, описанной около треугольника. Ответ : 36 см, 48 см. 19. В прямоугольном треугольнике точка касания вписанной окружности делит гипотенузу на отрезки 24 и 36 см. Найти катеты. Ответ : 18. Площадь прямоугольного треугольника равна S 1 , а площадь круга, вписанного в него, S 2 . Найти площадь круга, описанного около этого треугольника. Ответ : 16. Около окружности радиуса R описан равнобедренный треугольник с углом 120 0 . Найти стороны треугольника. Ответ : 15. В равнобедренный треугольник вписана окружность радиуса r. Высота, проведённая к основанию, делится окружностью в отношении 1 :2. Найти площадь треугольника. Ответ : a 17. Доказать, что радиус окружности, вписанной в прямоугольный треугольник, равен , где a,b – катеты, а с – гипотенуза Ответ :

5. Образцы решения задач

6. Периметр прямоугольного треугольника 60см, а высота , проведённая к гипотенузе, равна 12см. Найти стороны треугольника 15 см , 20см , 25см. Решение : Пусть стороны равны а, b и с. Тогда по условию задачи a + b + c = 60 , причём с 2 = а 2 + b 2 . Так как S ∆abc = 1/2ab и S ∆abc = 1/2h c . C , То a . b = h c . C Составим систему трёх уравнений с тремя неизвестными : Решая квадратное уравнение a 2 – 35 a + 300 = 0, получаем а1 = 15 , а2 = 20. Тогда второй катет b равен 20 либо 15. Таким образом , катеты ABC равны 15 и 20 , а гипотенуза 25. Ответ :

7. C A D B В прямоугольном треугольнике гипотенуза равна С , а биссектриса одного из острых углов равна Найдите катеты Решение : Обозначим через α острый угол , из которого проведена биссектриса AD. Тогда CAD = DAB= Из ∆ ABC находим AC = AB . cos α = C . cos α Из ∆ ACD получаем Ответ : ; Приравнивая выражения, получаем тригонометрическое уравнение , т.е Используя формулу cos 2 = (1 + cos α ) , т.е cos α = 2 cos 2 - 1 , получаем уравнение : (2 cos 2 –1)= cos Сделаем замену cos α = t , в результате получаем уравнение D = 25 , t 1 = , t 2 = Т.к по условию задачи угол - острый, то Получаем , , Тогда ,

8. Определите острые углы прямоугольного треугольника , стороны которого составляют арифметическую прогрессию 53 0 2 / ; 36 0 58 | А B C C a b β α Решение : Пусть a и b катеты c – гипотенуза, α , β – угол ∆ ABC Т.к a,b,c – члены арифметической прогрессии, то на основании свойств арифметической прогрессии b – a = c- b . Т.к , то получим ,откуда следует Решим уравнение : т.к очевидно , то разделив обе части на , получим , , , Ответ :

9. Дан квадрат ABCD со стороной, равной единице. Точка K лежит на стороне CD и делит её в отношении CK : KD = 1 : 2 .Найти расстояние от вершины C до прямой AK A D B C K E Решение : Опустим из вершины С перпендикуляр СЕ на прямую АК и рассмотрим треугольники СКЕ и АКД. Треугольники подобны , т.к Поэтому но А D = 1 , , (т.к СК : KD = 1 : 2 и СК + К D = 1 ) Из ∆АК D по теореме Пифагора : , поэтому Ответ :

10. В равнобедренном ∆ ABC основание AB равно 30 , высота AD равна 24. Найти длину боковой стороны 25 A E B C D Решение : Пусть СЕ – высота , опущенная на основание , тогда Из ∆ ABD по теореме Пифагора : В прямоугольном ∆ ACE и ∆DAB равны острые углы : , значит треугольники подобны , поэтому , т.е Ответ :

11. Длины сторон AC и AB в ∆ ABC равны b и с, угол А вдвое больше угла B . Найти BC. B C A b c D x x Решение : AD - биссектриса в ∆ ABC , Пусть BD = x, но ∆ ABD равнобедренный, т.е. AD = x Из ∆ ABD по т. косинусов , т.е , откуда По свойству биссектрисы из ∆ ABC : тогда BC = BD + DC По теореме синусов из ∆ ABC : Перемножим левые и правые части 3) и 4) : Ответ :

12. Найти углы треугольника, в котором высота и медиана, проведённые из одной вершины, делят угол при этой вершине на три равные части 30 0 , 60 0 , 90 0 С B A M D Решение : Пусть CD – высота, CM – медиана в ∆ABC . Тогда CM - биссектриса в ∆ ACD и по свойству биссектрисы : В ∆ CMB : CD – высота и медиана, т.е. , т.е. и , но , т.е Значит Ответ : углы равны

13. В равнобедренный треугольник вписана окружность радиуса r . Высота, проведённая к основанию, делится окружностью в отношении 1 :2. Найти площадь треугольника A D C E O Решение : По условию задачи BF:FD = 1:2 Но FD = 2r , значит BF = r, а высота BD = BF + FD = 3r. Прямоугольные ∆ОЕ B и ∆ DBC подобны, так как , поэтому , т.е. , BC = 2DC Пусть DC = x , тогда из ∆ DBC по теореме Пифагора , т.е , откуда Найдём площадь ∆ ABC . Ответ :

14. Площадь прямоугольного треугольника равна S 1 а площадь круга , вписанного в него , S 2 Найдите площадь круга, описанного около этого треугольника B C A O Решение : Пусть АС = x , BC = y , r – радиус вписанной окружности, R – радиус описанной окружности. Известно, что x + y = 2(R + r) , отсюда x 2 + 2xy + y 2 = 4(R + r) 2 Но по условию задачи , т.е 2 x y = 4S 1 кроме того , т.е x 2 + y 2 = (2R) 2 , поэтому получаем Откуда S 1 = 2 Rr + r 2 , , но , значит , ,следовательно, площадь круга равна : Ответ :

15. Определите углы параллелограмма, если две его высоты равны h 1 и h 2 , а периметр равен 2 p . A B C D F E b a α β h 1 h 2 Решение : Пусть AB = b , BC = a Из ∆ ABE : Из ∆ BFC : По условию задачи : отсюда Ответ :

16. Тема : Планиметрия Решение задач α + β + γ = 180 0 Основные теоретические сведения Треугольник 2. Длина каждой стороны меньше суммы и больше разности длин двух других сторон : c < a +b , c > a – b a b c α β γ 4. Терема синусов : где R – радиус описанной около треугольника окружности. В параллелограмме : сумма квадратов диагоналей равна сумме квадратов всех его сторон. 3. Терема косинусов :

17. При решении задач, связанных с треугольником, используется свойства четырёх замечательных точек, центра вписанной и описанной окружностей, и ортоцентра : 4) Три высоты треугольника пересекающейся в одной точке, которая называется ортоцентром. 3) Три перпендикуляра, проведённые к серединам сторон треугольника, пересекаются в одной точке, точка равноудалена от вершины треугольника и является центром описанной окружности. 2) Три биссектрисы треугольника пересекаются в одной точке, лежащей строго внутри треугольника. Точка пересечения биссектрисы равноудалена от сторон треугольника и является центром вписанной окружности. Три медианы треугольника пересекаются в одной точке, лежащей строго внутри треугольника(центр тяжести). Точка пересечения делит медианы на отрезки, длины которых относятся как 2 :4 , считая от соответствующей вершины

18. Важную роль при решении задач играют три признака подобия треугольника : h a , m a , β a – длины высоты, медианы и биссектрисы, проведённые к стороне а, противолежащей углу А. R и r радиусы описанной и вписанной окружностей S - площадь треугольника Основные расчётные формулы 3. Если три стороны одного треугольника пропорциональны трём сторонам другого, то такие треугольники подобны Если две стороны одного треугольника пропорциональны двум сторонам другого треугольника, а углы между этими сторонами равны, то эти треугольники равны Если два угла одного треугольника равны двум углам другого треугольника, то такие треугольники подобны. 4. S 3. S 2. S S - полупериметр треугольника

19. Прямоугольный треугольник Равносторонний треугольник S= A С B a b a C b C D h C - теорема Пифагора c c c b a h  c cb b  2 c ca a  2 2 c R  2 1   c b a r    2 1 ab S  2 1 A b a tan A c a sin A a b cot   A c b cos   8. ma= 7. R= , 6. S=

20. Параллелограмм Основные теоретические сведения Параллелограмм Определить углы параллелограмма, если две его высоты равны h 1 и h 2 , а периметр равен 2р. Ответ : B C A D a h c d 2 d 1 α φ