The document details a project by Siddharth Nawani, focusing on the evolution and modification of active queue management (AQM) algorithms, specifically the RED (Random Early Detection) algorithm, to reduce packet loss and improve network throughput. The project includes background analysis of conventional AQM methods, modifications to the RED algorithm, extensive simulation results, and plans for future work to integrate multiple congestion control strategies. Findings indicate that the modified RED variants can maintain lower average queue sizes and reduce packet loss in comparison to standard implementations.

1. Analysis & Evolution
Of
AQM Algorithms
SUBMITTED BY:
SIDDHARTH NAWANI

2. Presentation Outlines
 General Idea of the Project.
 General background about different AQM’s (RED & DropTail)
 Modified RED AQM
 Project Implementation Details
 Future Work
 Testing
 Issues
 Mathematical Elaboration

3. Abstract
 The project focuses on how congestion control and queue
management techniques have evolved over time and being
modified to minimize the rate of packet loss. Extensive relevant
research has been done on the existing AQM’s and from the midst
of RED, our algorithm has evolved. The key idea is to modify the
existing RED algorithm to achieve stabilization in Queue length,
decrease in packet loss rate at routers and increased throughput in
comparison to RED. The packet probability marking function of RED
has been modified into four different functions and the results and
effects on various parameters like Queue length, packet loss etc
have been simulated and compared. The design rationale of RED
has been studied and enhanced to achieve better stabilized queue
and throughput.

4. Need…
 Due to the enormous growth of the internet, demands for access
from multiple users have increased and the request for new services
for its application have also increased significantly. Due to this ,
there have been an increase in packet loss rates and drop in
network efficiency. The problem has been well discussed over
several years, still conventional Active Queue Management
Algorithms cannot provide low complexity deployment.

5. Background - General
 In today’s networks, transport layer protocols are the one
responsible for congestion avoidance
 When there is congestion in the router and its queue gets over flown
, it drops packets from the tail until there is space to receive new
packets in the buffer
 The protocol is completely transparent to the hosts, they see it as
“Black Box”. Their only indication of congestion is packet loss

6. The conventional algorithms
 RED
 Droptail

7. Drop Tail
 The traditional technique for managing router is the method known as "tail
drop“.
 This method has served the Internet well for years, but it has two important
drawbacks:
 LOCK OUT
 Drop-tail routers treat bursty traffic poorly
 Traffic gets synchronized easily  allows a few flows to monopolize the queue
space
 TCP-GLOBAL SYNCHRONIZATION
 In computer networks It can happen to TCP/IP flows during periods of
congestion because each sender will reduce their transmission rate at the
same time when packet loss occurs.

8. Other Problems in real network
scenarios
 TCP global Synchronization
 Congestive Collapse
 Network protocols which use aggressive retransmissions to compensate
for packet loss tend to keep systems in a state of network congestion
even after the initial load has been reduced to a level which would not
normally have induced network congestion. Thus, networks using these
protocols can exhibit two stable states under the same level of load. The
stable state with low throughput is known as congestive collapse
 Fairness among different flows

9. Active Queue Management
 In summary, an active queue management mechanism can provide the
following advantages for responsive flows:
1. Reduce number of packets dropped in routers
By keeping the average queue size small, active
queue management will provide greater capacity to
absorb naturally- occurring bursts without dropping
packets. Without active queue management, more
packets will be dropped when a queue does overflow.
2. Provide lower-delay interactive service
By keeping the average queue size small, queue
management will reduce the delays seen by flows.
This is particularly important for interactive
applications such as short Web transfers, Telnet
traffic, or interactive audio-video sessions,whose
subjective (and objective) performance is better when
the end-to-end delay is low.
3. Avoid lock-out behavior
Active queue management can prevent lock-out
behavior by ensuring that there will almost always be
a buffer available for an incoming packet. For the
same reason, active queue management can prevent a
router bias against low bandwidth but highly bursty
flows.

10. RED(Random Early Detection)
 RED was designed with the objectives to
(1) minimize packet loss and queuing delay,
(2) avoid global synchronization of sources,
(3) maintain high link utilization, and
(4) remove biases against bursty sources.
 RED gateways require the user to specify five parameters: the
maximum buffer size or queue limit (QL), the minimum (minth) and
maximum (maxth) thresholds of the "RED region", the maximum
dropping probability (maxp), and the weight factorused to
calculate the average queue size (wq).

11. RED – Cont.
Early packet dropping starts when the average queue size
exceeds minth.
RED was specifically designed to use the average queue size
(avg), instead of the current queue size, as a measure of incipien
congestion, because the latter proves to be rather intolerant of
packet bursts.
avg is calculated as an exponentially weighted moving average
using the following formula:
avg i = (1 - wq) × avgi-1 + wq × q

12. RED- Algorithm

13. Flow Graph

14. Packet Probability Marking function
of RED

15. Simulations
 The Topology Used:

16. Comparison on the basis of
throughput
 At Node 4:
Using RED: 0.241504MBytes/sec
Using DropTail: 0.207008MBytes/sec
 At Node 5:
Using RED : Avg Throughput 0.20084Mbytes/sec
Using DropTail: Ang Throughput 0.184832Mbytes/sec

17. Throughput Graph for RED

18. PHASE -2
 MODIFYING AN EXISTING ALGORITHM
(RED)

19. The Algorithm
What’s About to change ?...
Pb = Pmax*(avg – th_min)/(th_max-th_min)
Pa = Pb / (1 – count*Pb)
RED calculates the probability of dropping a packet by 2 steps
when average queue size falls in between th_min and th_max. The
first step is to calculate a probability called Pb, which is based on
the formula below,
It can be seen that the probability Pb is calculated based
on a linear function.
In the second step, RED counts the number of packets
have gone through the gateway (count) since last
packet is dropped from the flow and apply the following
formula,

20. SUBSYTEMS
What’s New ?..
In this part, we modified the first step by applying 2
different functions to calculate Pb and compare the
results. The curves for the 2 functions are roughly in
left.
2

21. Mathematical Representation :
 Original function:
 Modified Functions:
 V1: Pb = Pmax*(m*log(v_ave) + n)
 V2: Pb = Pmax*(m*exp(v_ave)+n)
Pb = Pmax*(v_a * v_ave + v_b)
where v_a = 1.0 / (th_max – th_min), v_ave is the average queue size, and v_b = -th_min / (th_max –
th_min).

22. SYSTEM INTEGRATION
Changes in the code
 Add a variable func to the data structure edp.
 Bind the variable in REDQueue constructor
 REDQueue::REDQueue
bind (“function_”,&edp_.func)’
 Calculate p_new_probability function
 Make changes in ns-default.tcl
 Queue/RED set function_ 0

23. Results
 Simulation Topology
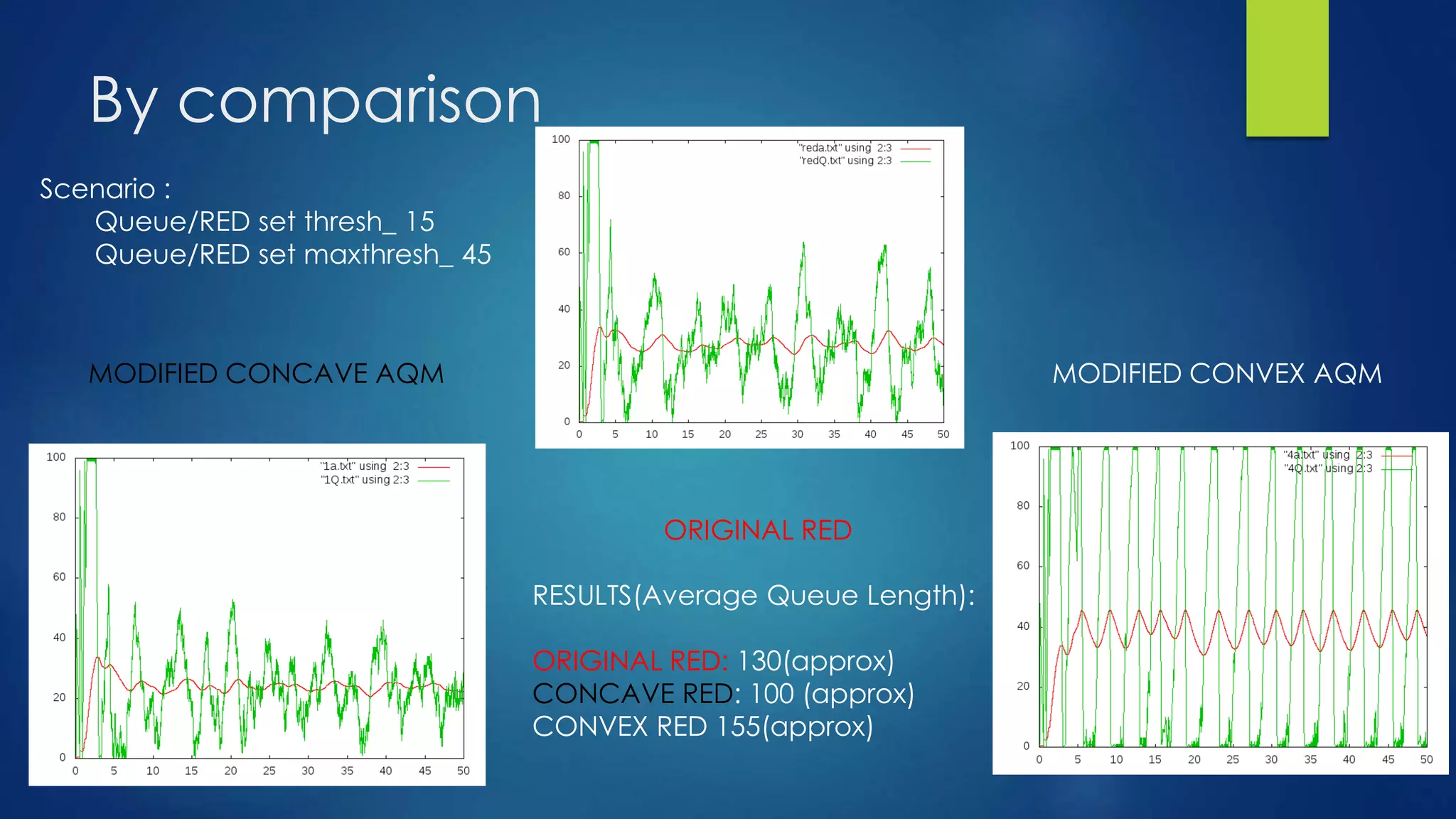
(scenario [15,45])
Modified RED
Drop Tail

24. COMPARATIVE ANALYSIS OF
VARIOUS AQM VARIATIONS
 Original RED

25.  Concave Packet Probability Marking Function(v1)

26.  Convex Packet Probability Marking Function(v4)

27.  Piece-wise linear Packet Probability Marking Function(v2)

28.  Piece-wise linear Packet Probability Marking Function(v3)

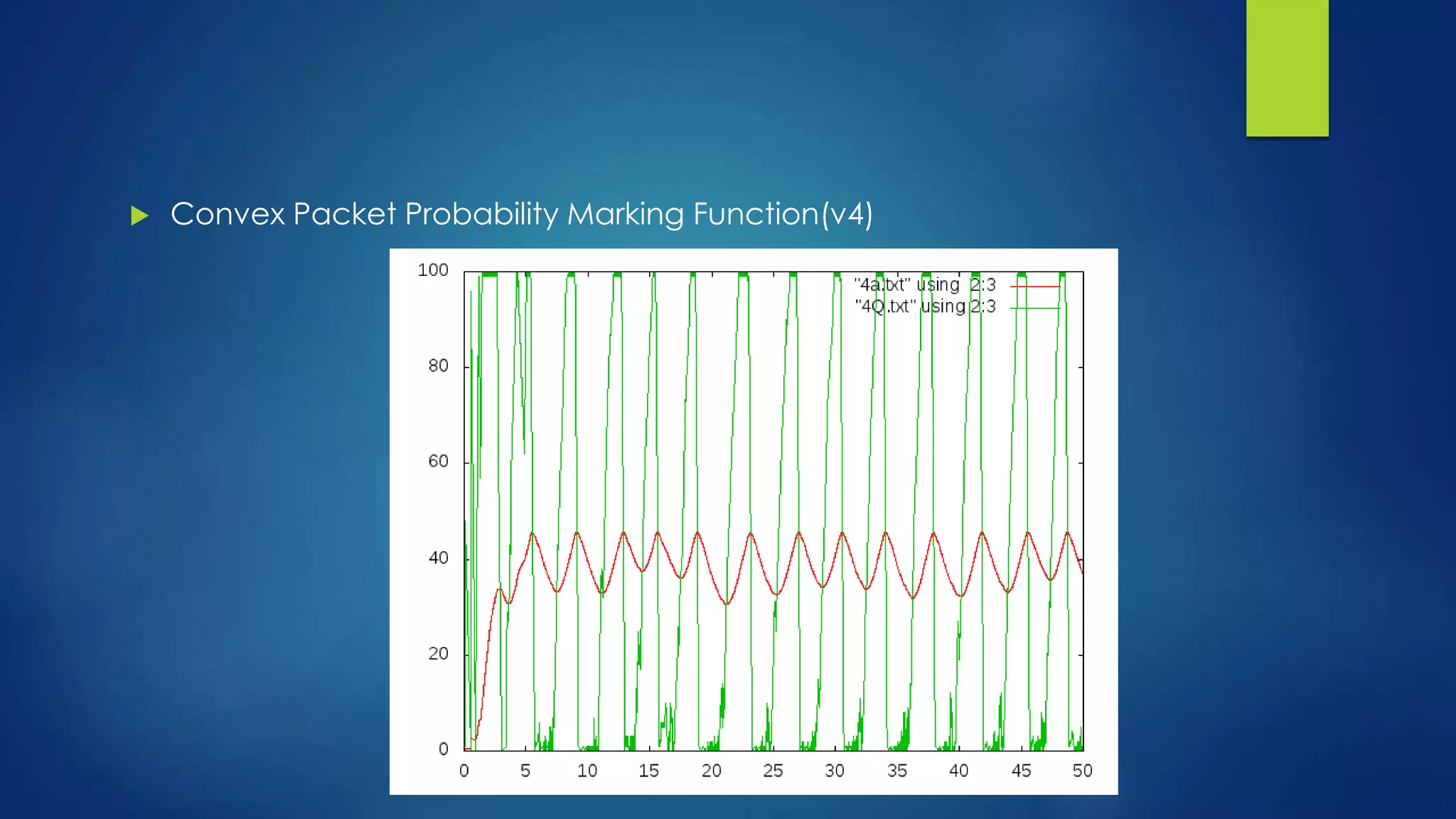
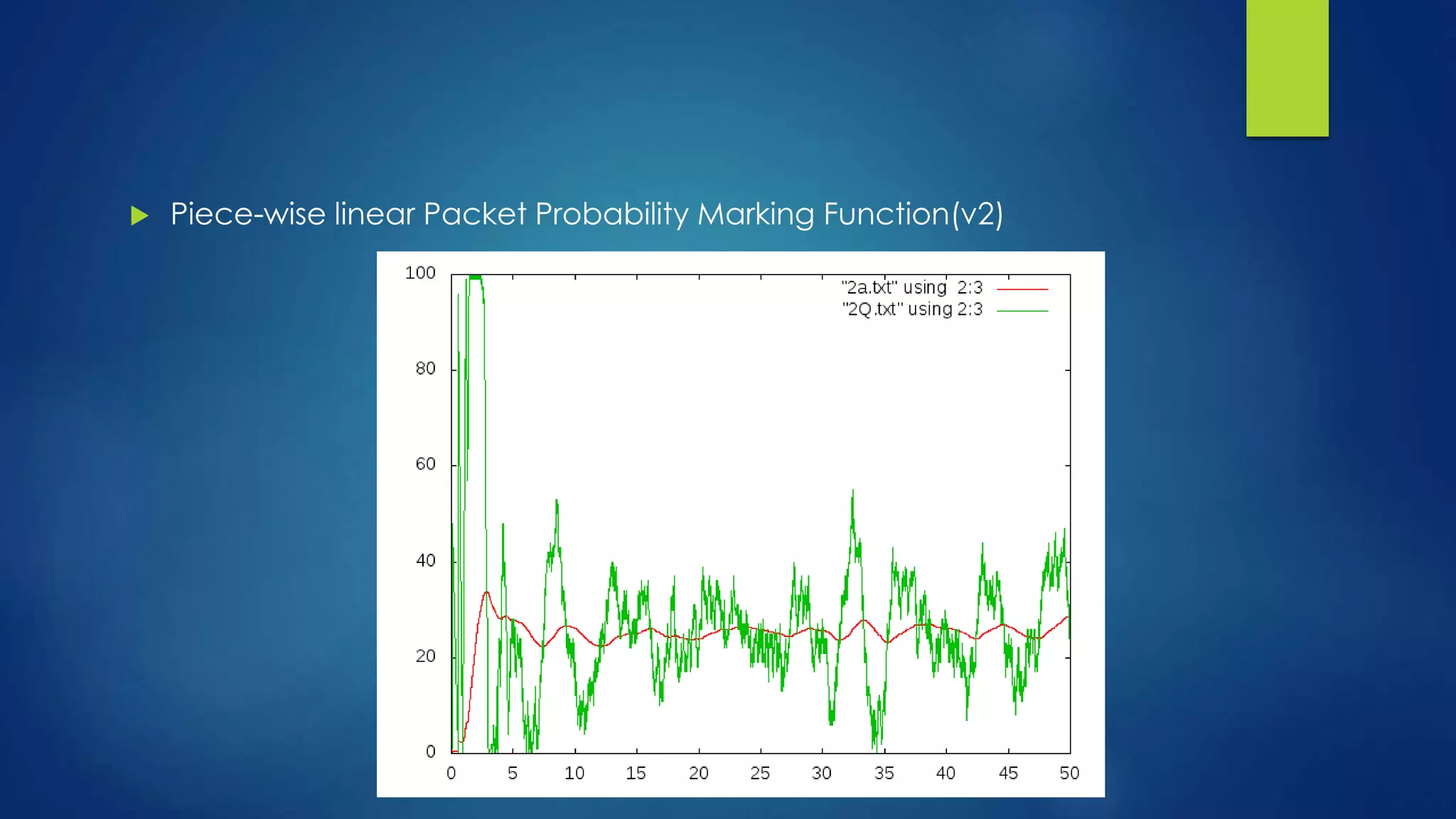
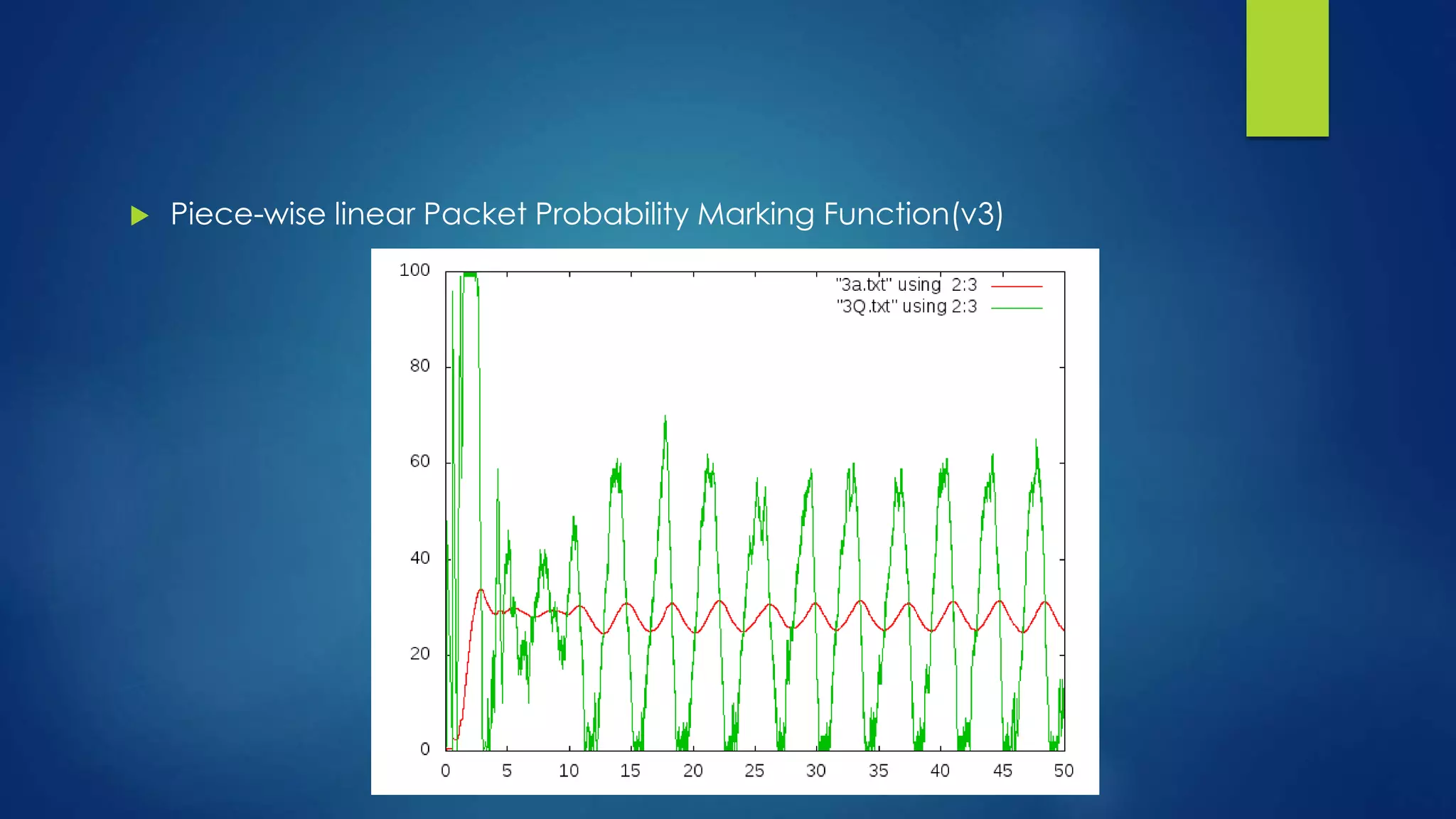
29. FINDINGS & CONCLUSION
 Queue Size
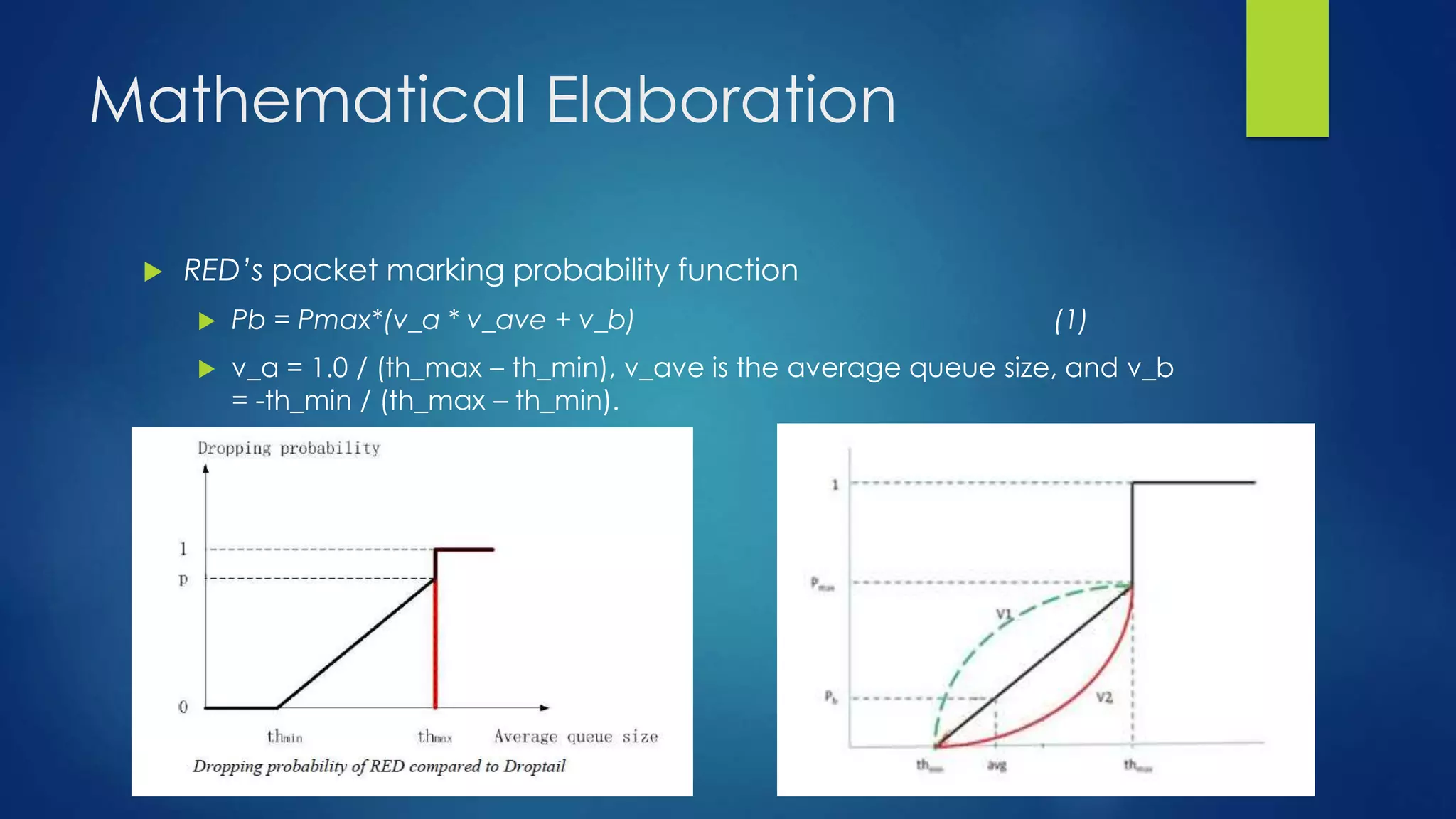
 From the plot, we can see that v1 keeps the
average queue size at a lower level than regular
RED, while v4 keeps the average queue size at a
higher level than regular RED. This is expected as
v1 is always above the original linear function
given the same average queue size value in the
range of [th_min, th_max], in other words, v1 is
more aggressive in terms of dropping packets
when the average queue size is between th_min
and th_max. On the contrast, v4 is less aggressive
than regular RED.

30.  Packet Loss
 From the simulation for loss packets, we can see that V4 ensures less
packet drop than regular RED and vice versa in case of V1, in which
packet is dropped at a higher rate than V1 and regular RED algorithm.
Same can be deduced for V2 and V3, with V2 being on the higher side.

31. Scenario[minp,maxp] Function/AQM Packet Sent Packet Lost % Packet Loss
[15,45] RED 18736 27 1.44
[15,45] Concave function (v1) 18717 23 1.22
[15,45] Piece wise Linear(v2) 18698 28 1.49
[15,45] Piece wise Linear(v3) 18459 27 1.46
[15,45] Convex function (v4) 18194 44 2.41
[20,60] RED 18671 25 1.33
[20,60] Concave function (v1) 18712 28 1.49
[20,60] Piece wise Linear(v2) 18636 26 1.39
[20,60] Piece wise Linear(v3) 18373 33 1.79
[20,60] Convex function (v4) 18025 33 1.83
[25,75] RED 18645 29 1.55
[25,75] Concave function (v1) 18657 26 1.39
[25,75] Piece wise Linear(v2) 18648 24 1.28
[25,75] Piece wise Linear(v3) 18579 25 1.34
[25,75] Convex function (v4) 17773 20 1.12
[30,90] RED 18511 26 1.40
[30,90] Concave function (v1) 18564 25 1.34
[30,90] Piece wise Linear(v2) 18564 27 1.45
[30,90] Piece wise Linear(v3) 18522 22 1.18
[30,90] Convex function (v4) 17773 20 1.125
Table Showing Packet Loss For differect Scenarios & Functions

32.  Throughput
 From the simulations, we can see that V4 function ensures higher
throughput than regular RED and V1 function.

33. Requirement specification
 Functionality
 The purpose of this AQM is to stabilize the Average Queue length at
routers.
 External Interface
 The AQM can be simulated in Network Simulator 2.34 and higher.
 Unix environment will be used to simulate the Otcl and C++ classes.
 The interaction of software will be through command line interface (like
Unix and NS2)

34.  Required Performance
 The complexity of the algorithm is O(N), where N is the total number of
routers participating in the exchange of Data at a particular time.
 The robustness of the algorithm is tested and simulated with 50 Nodes
including two main congestion control routers.
 The simulated time with fixed delay of 100ms, proved to be under 1 sec.
 Quality Attributes
 The design rationale of Modified RED AQM, is made closely with the actual
RED AQM, Hence all the standard measures of correctness, maintainability
and security have been followed strictly.
 Design Constraints imposed on the implementation
 The Testing has been done under a simulated scenario, keeping the delay in
consideration as close as possible to the real life scenario.

35. ISSUES
 Installing Ns2.34 in Ubuntu 13.04 (resolved)
 Appropriate parameters for running RED. Keeping the number of
nodes high to observe the changes. Leading to overhead.
 Appropriate parameters for running RED. Keeping the number of
nodes high to observe changes in throughput.
 It was observed that results in a particular scenario [20,60] beg to
differ slightly from other scenarios.

36. COMPLEXITY & TESTING OF MODULE
 Determining Complexity
 Most of the algorithms claim that they can provide fair sharing among different flows
without imposing too much deployment complexity. Most of the proposals focus on
only one aspect of the problem (whether it is fairness, deployment complexity, or
computational overhead), or fix the imperfections of previous algorithms, and their
simulations setting are different from each other. These all make it difficult to evaluate,
and to choose one to use under certain traffic load.
 The complexity can be defined in terms of the following:
 DEPLOYMENT COMPLEXITY
 The modified version of RED offers low deployment complexity as changes can be done
in the original RED algorithm only and no new components need to be installed.
 COMPUTATIONAL OVERHEAD
 Each arriving packet at the respective Router triggers the algorithm(same as RED)
 BIG-O-NOTATION
 O(Nt); N-> is the number of arriving packet arriving at the routers for a particular flow.
 The Algorithm is designed to work with the main routers

37.  Performance evaluation
 By comparison
 The comparison of the obtained queue length was done with the original
RED AQM.

38. By comparison
ORIGINAL RED
MODIFIED CONCAVE AQM MODIFIED CONVEX AQM
Scenario :
Queue/RED set thresh_ 15
Queue/RED set maxthresh_ 45
RESULTS(Average Queue Length):
ORIGINAL RED: 130(approx)
CONCAVE RED: 100 (approx)
CONVEX RED 155(approx)

39. TYPE OF TEST WILL TEST BE
PERFORMED
COMMENTS/EXPLA
NATION
SOFTWARE
COMPONENT
Requirement
Testing
Yes Involves testing of
all the required
components
Existing RED &
Droptail AQM
Unit yes Unit of Algorithms
including Average
queue length, loss
rates etc
RED
Integration Yes Integration of the
changes done in
the original RED
RED, Modified RED
Performance Yes Does not crash for
high number of
nodes
Modified RED
Stress Yes No. of load for
which the
algorithm works
fine
Modified RED
Compliance NO Standards
maintained by RED
Modified RED
Security NO Same standards as
maintained by RED
Modified RED
Load Yes Tested for 50 +
nodes
Modified RED
Role Name Specific
Responsibilities
Developer &
Tester
Siddharth
Nawani
Working on
developing
and
integration of
modules.
Testing of the
whole
Algorithm

40.  The average queue length was tested for four different scenarios
 Scenario 1:
 Queue/RED set thresh_ 15
 Queue/RED set maxthresh_ 45
 Scenario 2:
 Queue/RED set thresh_ 20
 Queue/RED set maxthresh_ 60
 Scenario 3:
 Queue/RED set thresh_ 25
 Queue/RED set maxthresh_ 75
 Scenario 4:
 Queue/RED set thresh_ 30
 Queue/RED set maxthresh_ 90

41. Risk Analysis & Mitigation Plan
Risk
Potential
Impact on
Project
Success
L/M/H
Likelihood of
Occurrence
L/M/H
Mitigation Plan
1.Project Size H H  Decomposition(Break into smaller
phases
 Phased implementation)
2. Project Scope H H  Decomposition
 Add another analysis phase
 Detailed specifications
 Early prototype/review of functionality
 Add more time to the project schedule.
3. Project Decision-Making L(no sponsor
and one
decision
maker)
L  The Coder as well as the project
implanter take care of this
4. Environmental State (Networking) H(it’s volatile
and yest to
be
deployed)
H  Additional testing, particularly stress
testing
 Training on new environment
 Find other projects using a similar
environment to compare notes
 Get a prototype deployed ASAP on new
environment
5. Team’s Experience M(Since no
similar
Project has
been done)
M  Less effect since the project team
comprises of one member only.
 Cross referencing results with other
verified results
6. Project Schedule L(Since the
process is still
in
developmen
t phase)
L  Supplement resources (outside
consultants, other groups)

42. FUTURE WORK

43. FUTURE WORK continues…
 Later on we will propose an algorithm combining the advantage of
BLUE, RED & CHOKe algorithm to minimize the loss rate.

44. THANK YOU
FOR YOUR VALUABLE
TIME… ;)

45. Mathematical Elaboration
 RED’s packet marking probability function
 Pb = Pmax*(v_a * v_ave + v_b) (1)
 v_a = 1.0 / (th_max – th_min), v_ave is the average queue size, and v_b
= -th_min / (th_max – th_min).

46. Mathematical Elaboration
 RED’s packet marking probability function
 Pb = Pmax*(v_a * v_ave + v_b) (1)
 v_a = 1.0 / (th_max – th_min), v_ave is the average queue size, and v_b
= -th_min / (th_max – th_min).
 For the concave function:
 Pb = Pmax*(m*log(v_ave) + n) (2)
 0 = Pmax*(m*log(th_min) + n) (3)
 Pmax = Pmax*(m*log(th_max + n)) (4)
 0 = Pmax*(v_a*th_min + v_b) (5)
 m = 1/(log(th_max) – log(-v_b/v_a)) (6)
 n = -m*log(-v_b/v_a) (9)

47.  For the convex function
 Pb = Pmax*(m*exp(v_ave)+n) (1)
 m = 1/(exp(th_max) – exp(-v_b/v_a)) (2)
 n = -m*exp(-v_b/v_a) (3)