Recommended
More Related Content
What's hot
What's hot (20)
Primenenie svojstv funkcij_k_resheniyu_uravnenij_i

Primenenie svojstv funkcij_k_resheniyu_uravnenij_i
КОНТРОЛЬ ЗАТРАТ НА УПРАВЛЕНИЕ ПРИ ВОСПРОИЗВЕДЕНИИ ГАРМОНИЧЕСКИХ ЭКЗОГЕННЫХ ВО...

КОНТРОЛЬ ЗАТРАТ НА УПРАВЛЕНИЕ ПРИ ВОСПРОИЗВЕДЕНИИ ГАРМОНИЧЕСКИХ ЭКЗОГЕННЫХ ВО...
Statistics2013 talk "Nonlinear expectation and Risk measure"

Statistics2013 talk "Nonlinear expectation and Risk measure"
математика на вступительных экзаменах в мгу в 2010г(газета математика)

математика на вступительных экзаменах в мгу в 2010г(газета математика)
Similar to 8
Similar to 8 (20)
Прогнозирование - Лекция 2. Корреляционный анализ и простая линейная регрессия

Прогнозирование - Лекция 2. Корреляционный анализ и простая линейная регрессия
1555 показательн. и логарифмич. функции в зад. и примерах власова а.п. и др-...

1555 показательн. и логарифмич. функции в зад. и примерах власова а.п. и др-...
More from Dr. Jury Belonozhkin
Путеводитель-хрестоматия содержит фрагменты работ советского российского методолога Г.П. Щедровицкого (1929—1994), представляю-щих основные средства и инструменты управленческого мышления. Книга предназначена для использования в качестве учебного пособия в циклах тренировок и практических занятий в рамках элементарной, начальной, обшей и высшей управленческой подготовки.Путеводитель по основным понятиям и схемам методологии Организации, Руководст...

Путеводитель по основным понятиям и схемам методологии Организации, Руководст...Dr. Jury Belonozhkin
БЛИНОВ ВЛАДИМИР ИГОРЕВИЧ
ФИРО
Тема 1. КЛЮЧЕВЫЕ НАПРАВЛЕНИЯ СОВЕРШЕНСТВОВАНИЯ СИСТЕМЫ СРЕДНЕГО ПРОФЕССИОНАЛЬ...

Тема 1. КЛЮЧЕВЫЕ НАПРАВЛЕНИЯ СОВЕРШЕНСТВОВАНИЯ СИСТЕМЫ СРЕДНЕГО ПРОФЕССИОНАЛЬ...Dr. Jury Belonozhkin
More from Dr. Jury Belonozhkin (20)
Тема 3. Международное сотрудничество в области высшего образования. Учебник

Тема 3. Международное сотрудничество в области высшего образования. Учебник
Тема 3. Учебник "Организация, руководство, управление", Щедровицкий Г.П.

Тема 3. Учебник "Организация, руководство, управление", Щедровицкий Г.П.
Тема 3. Приоритетные проект "Рабочие кадры для передовых технологий"

Тема 3. Приоритетные проект "Рабочие кадры для передовых технологий"
Тема 3. Модель непрерывного профессионального образования

Тема 3. Модель непрерывного профессионального образования
Путеводитель по основным понятиям и схемам методологии Организации, Руководст...

Путеводитель по основным понятиям и схемам методологии Организации, Руководст...
Тема 1. Напцприоритет рабочие кадры. Н.М. Золотарева

Тема 1. Напцприоритет рабочие кадры. Н.М. Золотарева
Тема 1. КЛЮЧЕВЫЕ НАПРАВЛЕНИЯ СОВЕРШЕНСТВОВАНИЯ СИСТЕМЫ СРЕДНЕГО ПРОФЕССИОНАЛЬ...

Тема 1. КЛЮЧЕВЫЕ НАПРАВЛЕНИЯ СОВЕРШЕНСТВОВАНИЯ СИСТЕМЫ СРЕДНЕГО ПРОФЕССИОНАЛЬ...
1.1. сущность, задачи и функции рынка ценных бумаг

1.1. сущность, задачи и функции рынка ценных бумаг
8
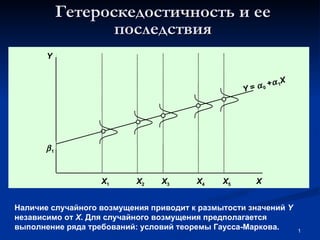
- 1. Гетероскедостичность и ее последствия 1 X Y = 0 + 1 X Y Наличие случайного возмущения приводит к размытости значений Y независимо от X . Для случайного возмущения предполагается выполнение ряда требований: условий теоремы Гаусса-Маркова. X 3 X 5 X 4 X 1 X 2
- 2. Гетероскедостичность и ее последствия 1 X Y = 0 + 1 X Y Распределение u для каждого наблюдения имеет нормальное распределение и нулевое ожидание, но дисперсия распределений различна . X 3 X 5 X 4 X 1 X 2
- 15. Алгоритм применения теста Готвальда-Квандта Государственные расходы на образование в различных странах F кр=3.0 Применение ф-ии «ЛИНЕЙН» Модель: Y=-2.32 + 0.067X (9.4) 2586 181,3 США 76,9 4,26 Австрия 1040 61,61 Япония 67 1,6 Турция 815 38,62 ФРГ 66,3 4,45 Дания 655,3 33,59 Франция 63 3,5 Югославия 535 29,9 Англия 57,7 4,9 Норвегия 395,5 15,95 Италия 51,6 2,8 Финляндия 261,4 18,9 Канада 40,2 0,75 Греция 249,7 8,92 Бразилия 27,6 1,25 Чили 211,8 4,79 Испания 27,6 0,67 Гонконг 186,3 5,46 Мексика 24,7 1,07 Португалия 169,4 13,41 Нидерланды 23,8 1,27 Н.Зеландия 153,9 5,56 Аргентина 22,2 1,02 Венгрия 141 8,66 Австралия 20,9 1,81 Израиль 124,2 11,22 Швеция 18,9 1,23 Ирландия 119,5 7,15 Бельгия 11,3 0,32 Сингапур 116 6,4 С.Аравия 10,1 0,22 Уругвай 101,7 5,31 Швейцария 5,67 0,34 Люксембург ВВП Расходы Страна ВВП Расходы Страна 2,6835 3,0371 10 11,318 0,518 0,5309 0,3276 0,0123 0,0821 0,0414 388,24 26185 10 674,45 6,2309 0,9854 2,4453 0,0027 -8,187 0,0711
- 20. Метод исправления гетероскедастичности Применение ф-ии «ЛИНЕЙН» Относительные расходы на образование в различных странах F кр=3.0 Модель: Y=-0.066 + 0.053X (9.5) 0,0004 0,070 США 0,0130 0,055 Австрия 0,0010 0,059 Япония 0,0149 0,024 Турция 0,0012 0,047 ФРГ 0,0151 0,067 Дания 0,0015 0,051 Франция 0,0159 0,056 Югославия 0,0019 0,056 Англия 0,0173 0,085 Норвегия 0,0025 0,040 Италия 0,0194 0,054 Финляндия 0,0038 0,072 Канада 0,0249 0,019 Греция 0,0040 0,036 Бразилия 0,0363 0,045 Чили 0,0047 0,023 Испания 0,0363 0,024 Гонконг 0,0054 0,029 Мексика 0,0405 0,043 Португалия 0,0059 0,079 Нидерланды 0,0420 0,053 Н.Зеландия 0,0065 0,036 Аргентина 0,0451 0,046 Венгрия 0,0071 0,061 Австралия 0,0478 0,086 Израиль 0,0081 0,090 Швеция 0,0530 0,065 Ирландия 0,0084 0,060 Бельгия 0,0882 0,028 Сингапур 0,0086 0,055 С.Аравия 0,0987 0,022 Уругвай 0,0098 0,052 Швейцария 0,1764 0,060 Люксембург 1/ВВП Y/ВВП Страна 1/ВВП Y/ВВП Страна 0,0044 2E-05 10 0,0417 0,021 0,0042 0,0105 0,1453 0,0438 0,0297 0,0032 0,0003 10 1,0329 0,0179 0,0936 0,0098 2,5862 0,0585 -2,628
- 21. Метод исправления гетероскедастичности (9.5) (9.4) Диаграмма рассеяния и графики моделей с гетероскедастичными и гомоскедастичными случайными возмущениями.