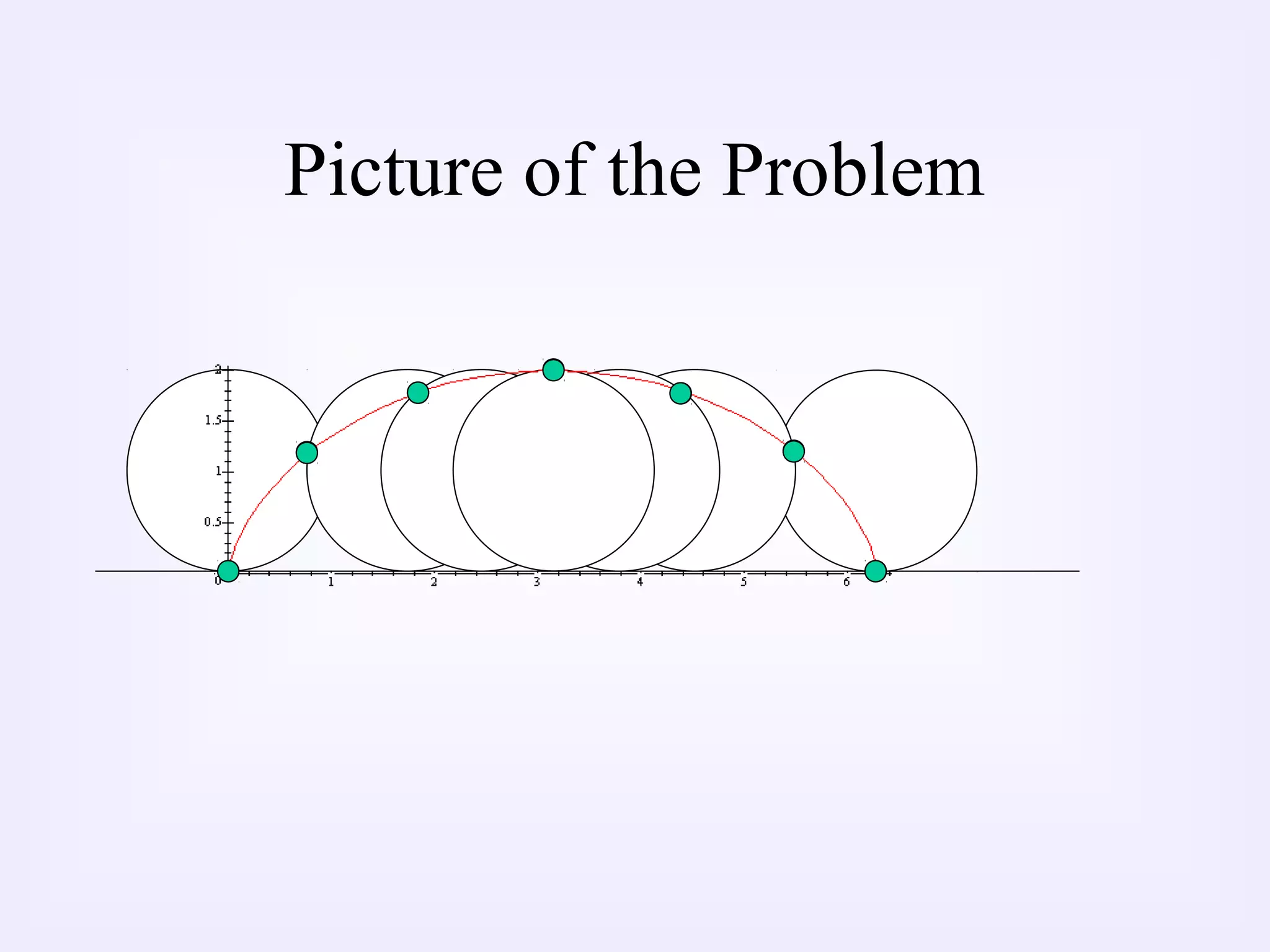
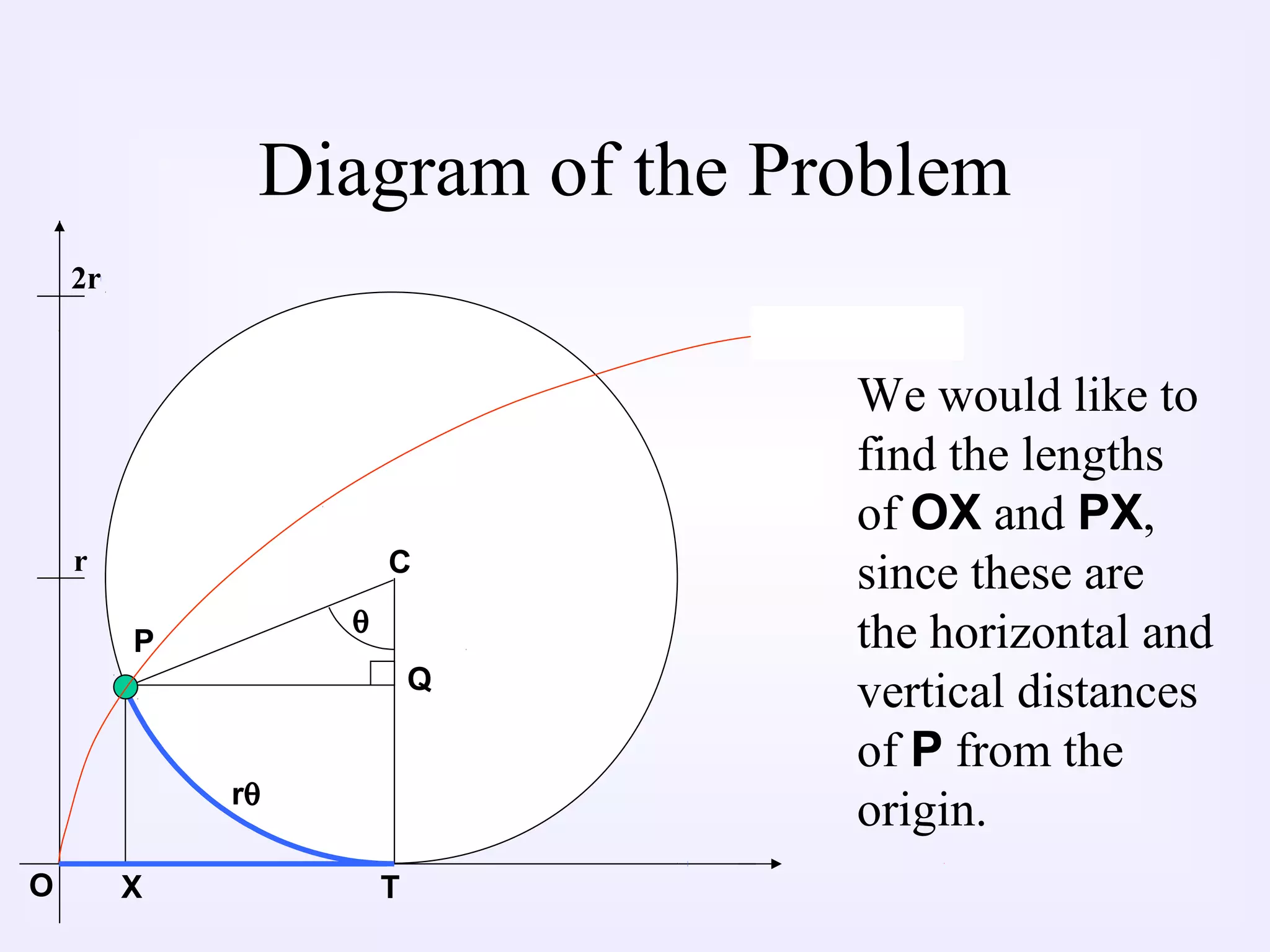
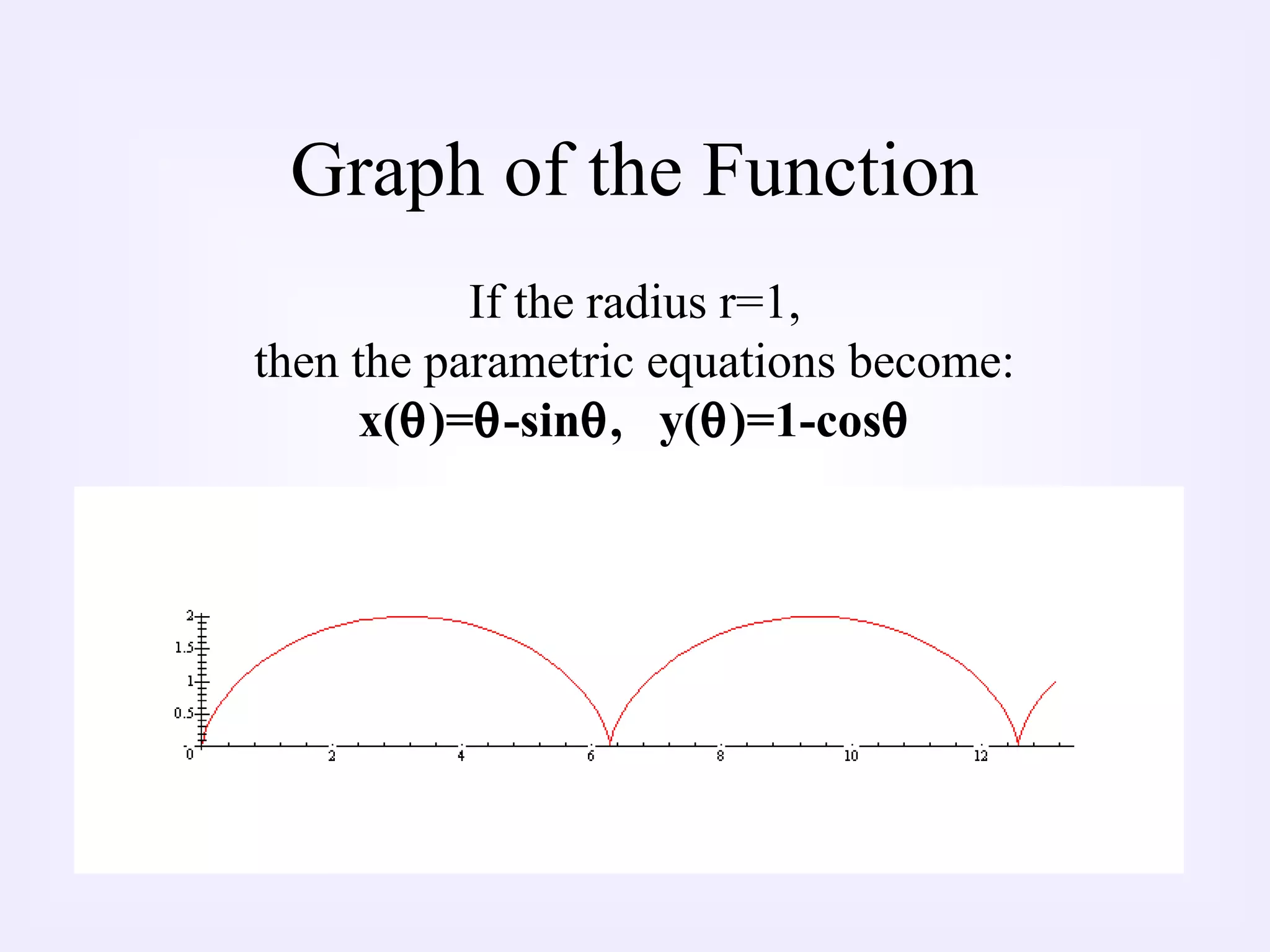
1) The document discusses parametric equations and uses the example of a wheel rolling across a surface to derive parametric equations. 2) As the wheel rolls, the location of a point on the wheel traces out a curve. To describe this curve, the document derives parametric equations that express the x and y coordinates of the point in terms of a third parameter, the angle of rotation. 3) The parametric equations derived are x(θ)=rθ - rsinθ and y(θ)=r - rcosθ, where r is the radius of the wheel and θ is the angle of rotation.

1. Robert M. Guzzo
Math 32a
Parametric Equations

2. We’re used to expressing curves in terms
of functions of the form, f(x)=y.
What happens if the curve is too
complicated to do this?
Let’s look at an exampleLet’s look at an example.

3. Question: What is the path traced out by its
bloody splat?
Why would we ask such a question?
Mathematicians are sick bastards!!!
An ant is walking along... only to be crushed by a
rolling wheel.

4. Problem Posed Again
(in a less gruesome manner)
A wheel with a radius of r feet is marked at
its base with a piece of tape. Then we allow the
wheel to roll across a flat surface.
a) What is the path traced out by the tape
as the wheel rolls?
b) Can the location of the tape be determined at
any particular time?

5. Questions:
•What is your prediction for the shape
of the curve?
•Is the curve bounded?
•Does the curve repeat a pattern?

6. Picture of the Problem

7. Finding an Equation
•f(x) = y may not be good enough to express the
curve.
•Instead, try to express the location of a point, (x,y),
in terms of a third parameterparameter to get a pair of
parametric equationsparametric equations.
•Use the properties of the wheel to our advantage.
The wheel is a circle, and points on a circle can be
measured using angles.
WARNING: Trigonometry ahead!WARNING: Trigonometry ahead!WARNING: Trigonometry ahead!WARNING: Trigonometry ahead!WARNING: Trigonometry ahead!

8. Diagram of the Problem
2r
r
O
P
C
Q
θ
TX
We would like to
find the lengths
of OX and PX,
since these are
the horizontal and
vertical distances
of P from the
origin.rθ

9. r
O
P
C
Q
θ
TX
The Parametric Equations
|OX| = |OT| - |XT|
rθ
rθ
r sinθ
r cosθ
r
|PX| = |CT| - |CQ|
= |OT| - |PQ|
x(θ) = rθ - r sinθ
y(θ) = r - r cosθ

10. Graph of the Function
If the radius r=1,
then the parametric equations become:
x(θ)=θ-sinθ, y(θ)=1-cosθ

11. Real-World Example:
Gears

12. For Further Study
• Calculus, J. Stuart, Chapter 9, ex. 5, p. 592:
The basic problem. Stuart also looks at
more interesting examples:
• What happens if we move the point, P, inside the
wheel?
• What happens if we move P some distance outside
the wheel?
• What if we let the wheel roll around the edge of
another circle?
•History of the CycloidHistory of the Cycloid