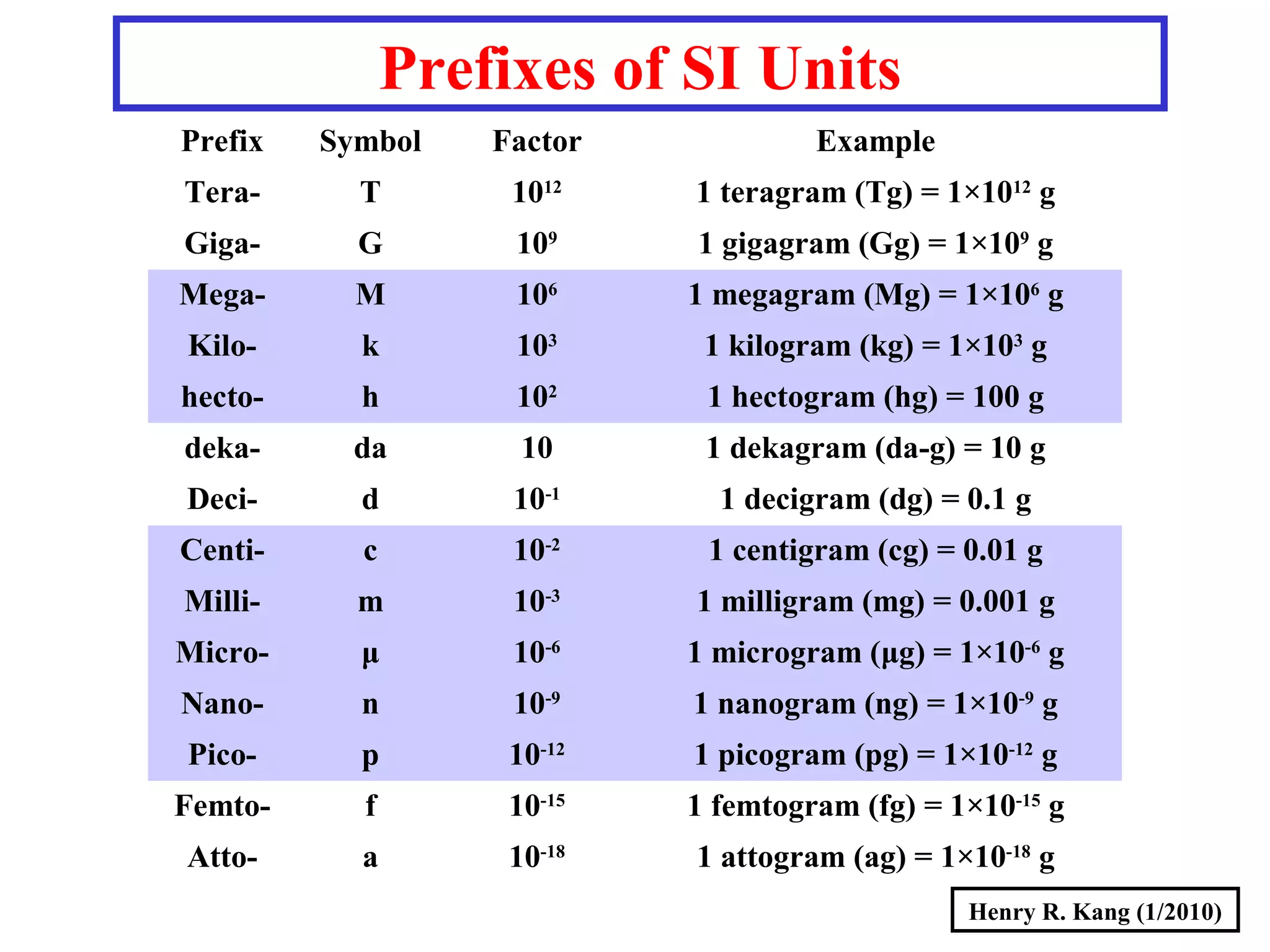
This document summarizes key concepts about measurement from a general chemistry lecture, including: - SI base units for length, mass, time, temperature and others. Prefixes are used to modify the units. - Derived SI units are composed from multiple base units, like area, volume, density and more. - English units are also discussed and converted to metric units. - Concepts like mass vs weight, temperature scales, density, and the problematic "lb" unit are explained. Examples are provided to demonstrate calculations and conversions between units.

1. Henry R. Kang (1/2010)
General Chemistry
Lecture 3
Measurement

2. Henry R. Kang (1/2010)
Contents
• SI Base Units
 Length, mass, time, temperature, etc.
 Prefixes
• SI Derived Units
• English Units
• Number
 Scientific notation
 Significant figures
 Accuracy
 Precision
• Dimensional Analysis

3. Henry R. Kang (1/2010)
SI
Base Units

4. Henry R. Kang (1/2010)
SI Base Units of Measurement
• SI Units (International
System of Units)
 Length is meter (m)
 In chemistry, centimeter (cm)
is more often used than m.
 Non-SI unit, angstrom (Å) =
10-10
m, is also used in
spectroscopic measurements.
 Mass is kilogram (kg)
 In chemistry, gram (g) is
more often used than kg.
 Time (s or sec)
 Temperature is kelvin (K)
 Fahrenheit: °F and
 Celsius: °C are also used
Base Quantity Name
of Unit
Symbol
Length meter m
Mass kilogram kg
Time second s (sec)
Temperature kelvin K
Electrical current ampere A
Amount mole mol
Luminous intensity candela cd
SI Base Units

5. Henry R. Kang (1/2010)
Prefixes of SI Units
Prefix Symbol Factor Example
Tera- T 1012
1 teragram (Tg) = 1×1012
g
Giga- G 109
1 gigagram (Gg) = 1×109
g
Mega- M 106
1 megagram (Mg) = 1×106
g
Kilo- k 103
1 kilogram (kg) = 1×103
g
hecto- h 102
1 hectogram (hg) = 100 g
deka- da 10 1 dekagram (da-g) = 10 g
Deci- d 10-1
1 decigram (dg) = 0.1 g
Centi- c 10-2
1 centigram (cg) = 0.01 g
Milli- m 10-3
1 milligram (mg) = 0.001 g
Micro- μ 10-6
1 microgram (μg) = 1×10-6
g
Nano- n 10-9
1 nanogram (ng) = 1×10-9
g
Pico- p 10-12
1 picogram (pg) = 1×10-12
g
Femto- f 10-15
1 femtogram (fg) = 1×10-15
g
Atto- a 10-18
1 attogram (ag) = 1×10-18
g

6. Henry R. Kang (1/2010)
Mass and Weight
• Mass is the quantity of matter that gives the
heaviness for an object of the matter.
 The mass of an object is the same wherever and whenever it
is measured.
 SI units
 Kilogram (kg) and gram (g)
 1 kg = 1000 g
• Weight is the force that gravity exerts on an object.
 Weight depends on the location when it is measured.
 W = m g
 W is the weight, m is the mass, and g is the gravitational
acceleration constant.
 g = 9.81 m/s2

7. Henry R. Kang (1/2010)
Measuring Devices for Mass
• Top loading balance
 Depending on the model and manufacturer,
they can measure mass to 1/10, 1/100, or
1/1000 of a gram.
• Analytical balance
 It can read to 1/10,000 of a gram.

8. Henry R. Kang (1/2010)
Temperature Measure
• SI unit for temperature is kelvin (K)
• Celsius (°C) is defined from the boiling and
freezing points of water.
 It has the same magnitude as kelvin, but
differ by an offset value of 273.15.
 1 K = 1 °C
• Fahrenheit (°F) is used in United States.
 1 K = 1.8 °F

9. Henry R. Kang (1/2010)
Conversions between Temperature Scales
• Knowing one formula, one can derive the other
• K to °C
 °C = (1 °C/K) × (K) − 273.15°C
• °C to K
 K = (°C + 273.15 °C ) × (1 K / 1 °C)
• °C to °F
°F = (1.8 °F/°C) × (°C) + 32°F
• °F to °C
°C = (°F − 32°F) × (1°C / 1.8°F)

10. Henry R. Kang (1/2010)
Measuring Devices for Temperature
• Mercury Thermometer
 Depend on the division of the marks, usually
it can read to 1/10 of a degree.
• Alcohol Thermometer
 Depend on the division of the marks, usually
it can read to 1/10 of a degree.
• Digital Thermometer
 Depend on the digital readout.

11. Henry R. Kang (1/2010)
Examples of Temperature Conversion
• Solder is an alloy made of tin and lead that is used to connect electronic wires
and circuits. A solder has a melting point of 435°F. What is its melting point
in degrees Celsius?
 Answer: Use the equation, °C = (°F − 32°F) × (1°C / 1.8°F)
 (435 °F – 32 °F) × (1 °C / 1.8 °F) = 224 °C
• Helium has the lowest boiling point of all the elements at -269 °C. Convert
this temperature to degrees Fahrenheit.
 Answer: Use the equation, °F = (1.8 °F/°C) × (°C) + 32°F
 -269 °C × (1.8 °F/ °C) + 32°F = -452 °F
• Mercury, the only metal that exists as a liquid at room temperature, melts at
234.3 K. –38.9°C. Convert its melting point to degrees Fahrenheit.
 Answer: Use the equations, °C = (1 °C/K) × (K) − 273.15°C, then
°F = (1.8 °F/°C) × (°C) + 32°F
 (234.3 K) × (1 °C/K) – 273.15 K = -38.9 °C
 (-38.9 °C) (1.8 °F/°C) × (°C) + 32°F = -38.0 °F

12. Henry R. Kang (1/2010)
Derived Units

13. Henry R. Kang (1/2010)
SI Derived Units
• Derived units are the compounded units from multiple
base units.
 Area is the length squared. SI unit: m2
 Volume is the length cubed. SI unit: m3
 Density is the mass per unit volume SI unit: kg/m3
 Speed is the distance per unit time SI unit: m/s
 Acceleration is the speed per unit time SI unit: m/s2
 Force is the mass multiplied by acceleration SI unit: kg.m/s2
 Pressure is the force per unit area SI unit: kg/(m.s2
)
 Energy is the force multiplied by distance SI unit: kg.m2
/s2

14. Henry R. Kang (1/2010)
Volume Measure
• Cubic Meter (m3
)
• Cubic Centimeter (cm3
)
• Cubic Decimeter (dm3
)
• Liter (L)
• Milliliter (mL)
• Conversion Factors
1 m3
= 1,000 dm3
= 1,000,000 cm3
1 cm3
= (1 × 10-2
m)3
= 1 × 10-6
m3
1 dm3
= (1 × 10-1
m)3
= 1 × 10-3
m3
1 mL = 1 cm3
1 L = 1000 mL = 1000 cm3
= 1 dm3

15. Henry R. Kang (1/2010)
Measuring Devices for Volume
• Burette
 The accuracy depend on the division of the marks.
 50-mL and 25-mL burettes can be read to 1/100 of a mL.
• Pipette
 Deliver exact volume at the mark.
• Graduated cylinder
 Depend on the division of the marks:
 10-mL cylinder can be read to 1/100 of a mL
 100-mL cylinder can be read to 1/10 of a mL
• Volumetric flask
 Store exact volume at the mark.
• Others

16. Henry R. Kang (1/2010)
Density Measure and Units
• Density = mass / volume
 d = m / V
• SI Unit
 kg/m3
• Solid Samples
 g/cm3
• Liquid Samples
 g/mL
• Gas Samples
 g/L

17. Henry R. Kang (1/2010)
• A piece of gold with a mass of 243.2 g has a
volume of 12.6 cm3
. Calculate the density of
gold.
 Answer: Use the equation, d = m / V
 d = m/V = 243.2 g / 12.6 cm3
= 19.3 g/cm3
• A piece of platinum metal with a density of 21.5
g/cm3
has a volume of 8.45 cm3
. What is its
mass?
 Answer:
 m = d × V = 21.5 g/cm3
× 8.45 cm3
= 182 g
Examples of Density

18. Henry R. Kang (1/2010)
Example of Identification via Density
• A colorless liquid is believed to be one of the following:
Substance Density (g/mL)
n-butyl alcohol 0.810
ethylene glycol 1.114
isopropyl alcohol 0.785
toluene 0.866
Identify the substance by measuring the density. A
volume of 21.1 mL has a mass of 18.36 g. What is this
substance?
• Answer: Use the equation, d = m / V
 d = 18.36 g / 21.1 mL = 0.870 g/mL
 Based on the measured density, the substance is “toluene”.

19. Henry R. Kang (1/2010)
Example of Mass-Volume Conversion
• An experiment requires 33.0 g of isopropyl
alcohol. The density of isopropyl alcohol is 0.785
g/mL. What volume of isopropyl alcohol will be
needed to meet the mass required?
• Answer:
 Use the equation: d = m/V
Rearrange the equation
V= m/d
 V = 33.0 g / (0.785 g/mL) = 42.0 mL

20. Henry R. Kang (1/2010)
Conversion between
English and Metric Units
Quantity English Metric
Mass 1 pound (lb) = 453.6 grams or 0.4546 kg
2.2 pounds = 1 kilograms
Length 1 inch = 2.54 centimeters
1 yard = 0.91 meters
Volume 1 quart = 0.946 liter
1 gallon = 3.78 liters
Note that the pound (lb) is a rather troublesome unit. It is a unit of mass but also used as a
unit for force. In the case of force, 1 lb is the force due to gravitational attraction on an
object of that mass:
F = ma = 0.4536 kg × 9.81 m/s2
= 4.45 kg.m/s2
= 4.45 N;
1 lb = 4.45 N

21. Henry R. Kang (1/2010)
Problem of “lb” Unit
• Problem:
 On 9/23/99, $125,000,000 Mars Climate Orbiter entered
Mar’s atmosphere 100 km lower than planned and was
destroyed by heat.
• Reason
 NASA engineer mistook the conversion factor as
1 lb = 1 N
 “lb” is an English unit of force: 1 lb = 4.45 N
 Force = mass × acceleration
= 0.454 kg × 9.81 m/s2
= 4.45 kg.m/s2
= 4.45 N (1 N = 1 kg.m/s2
)