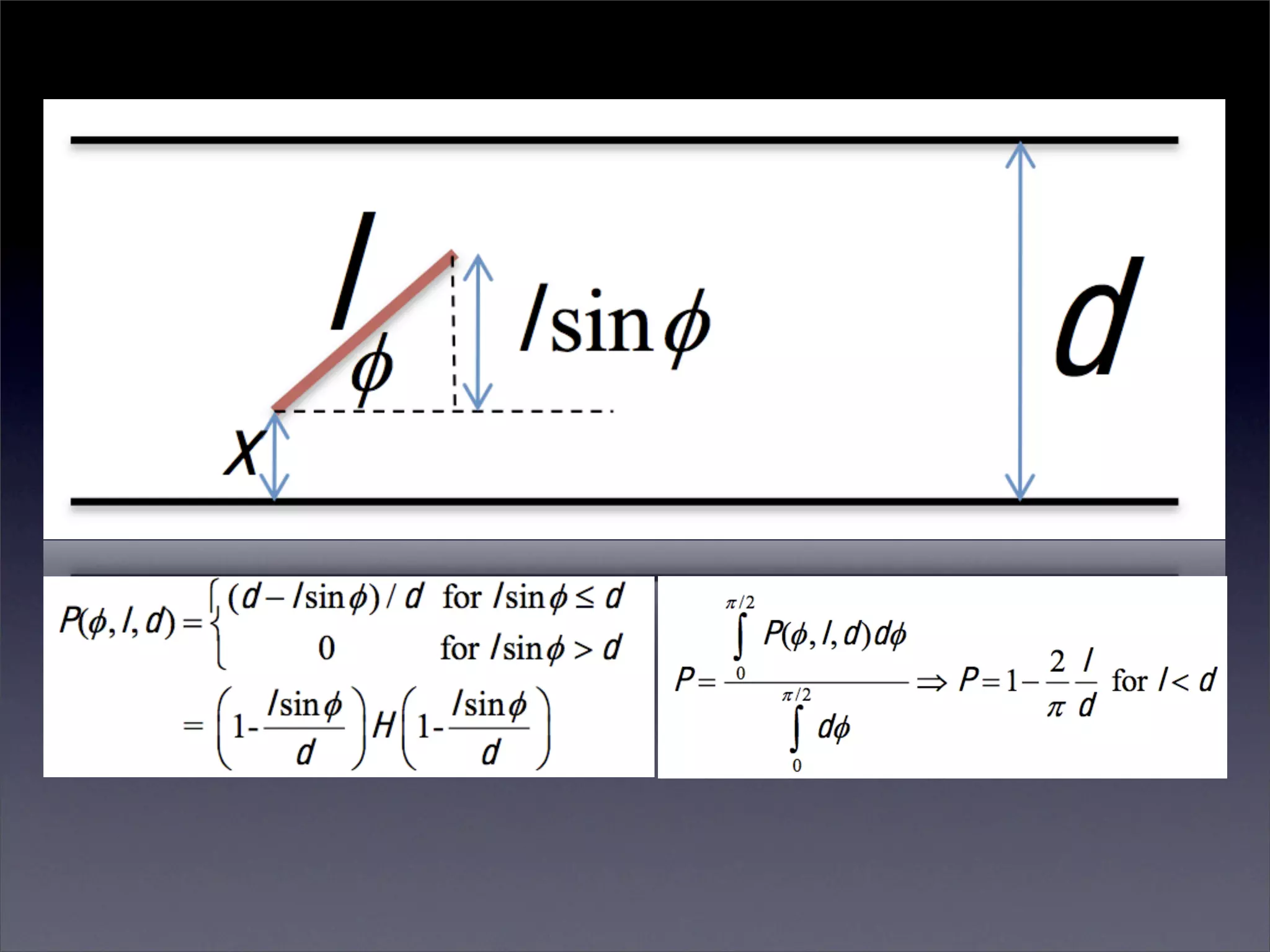
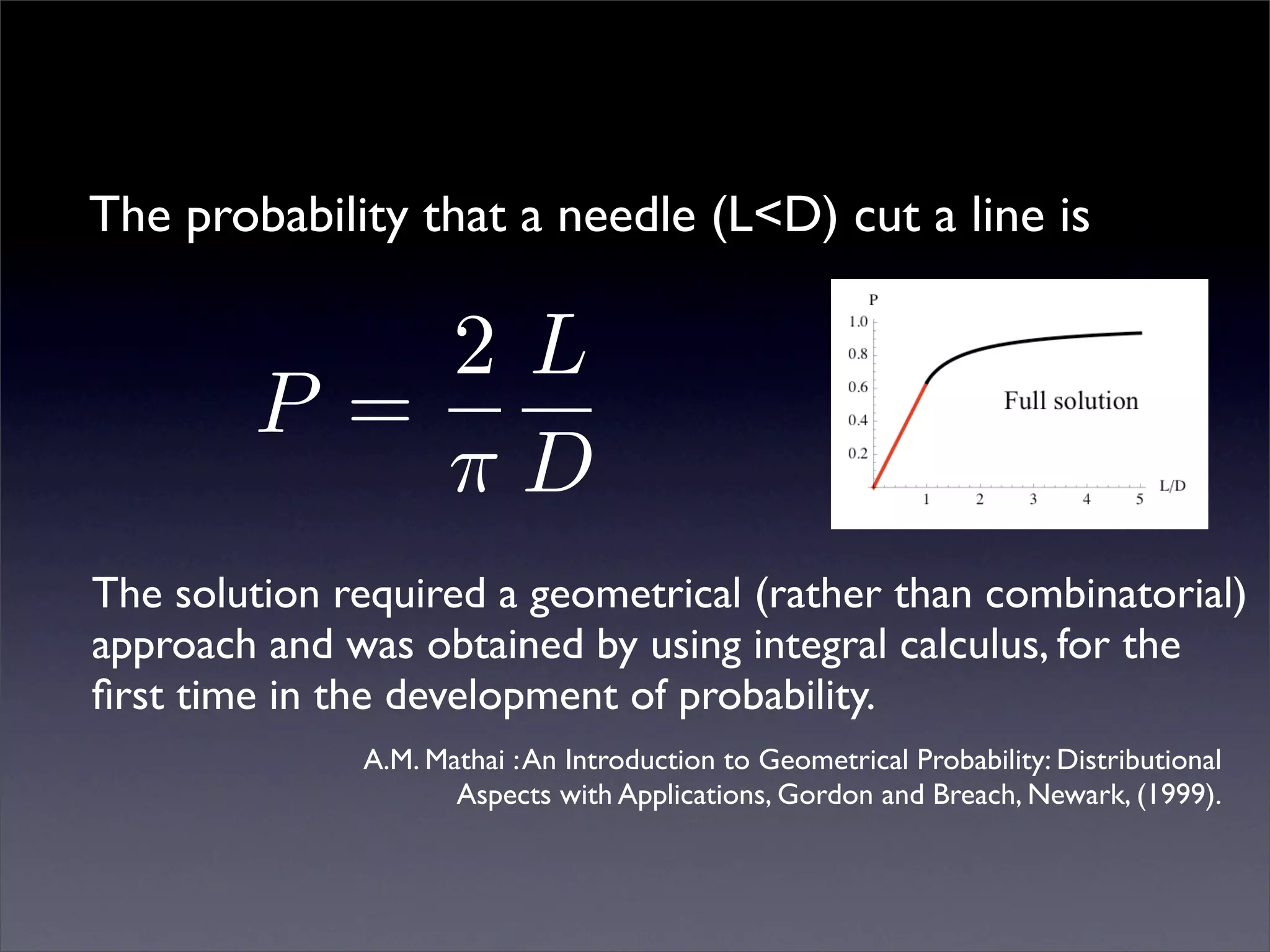
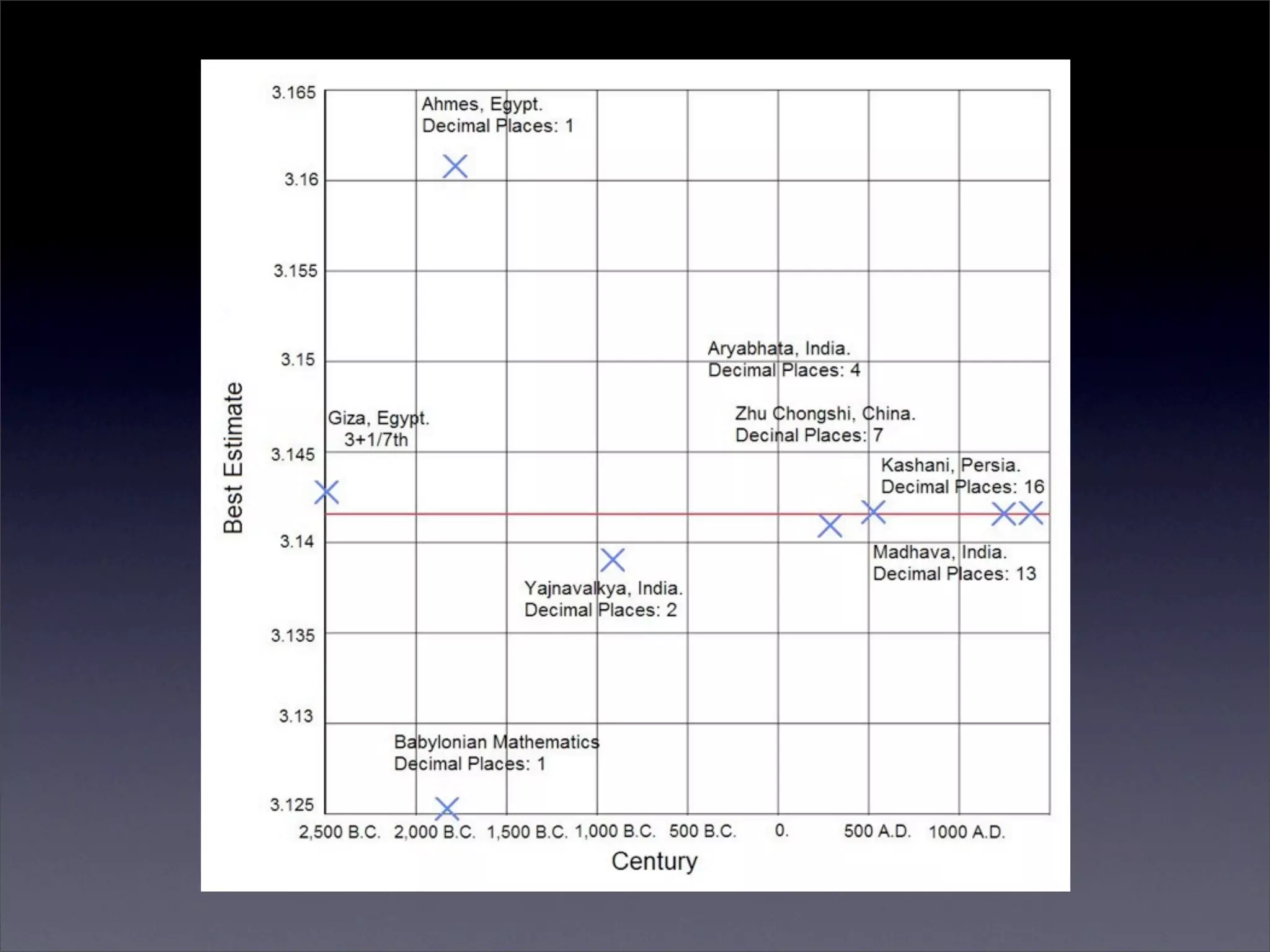
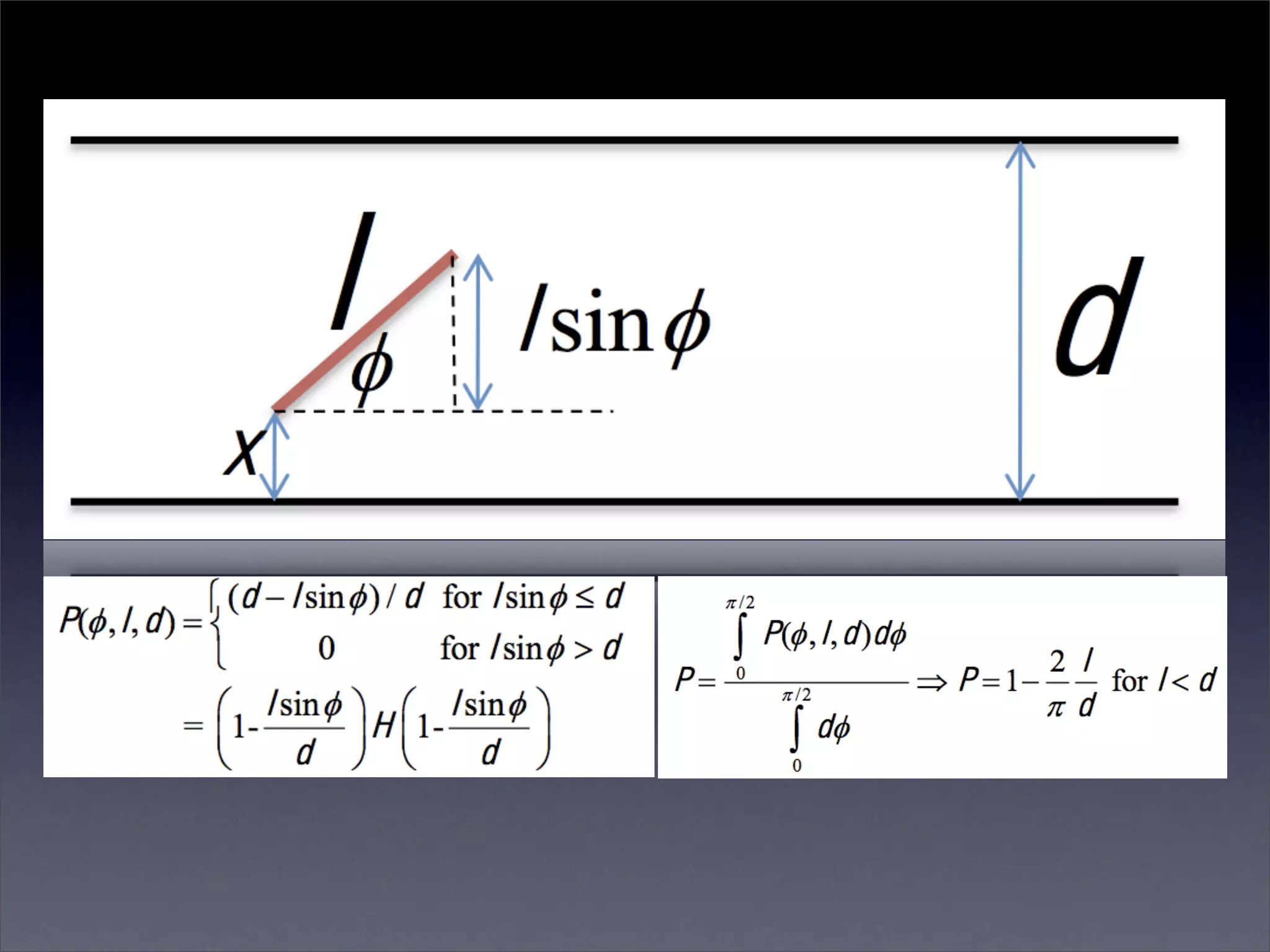
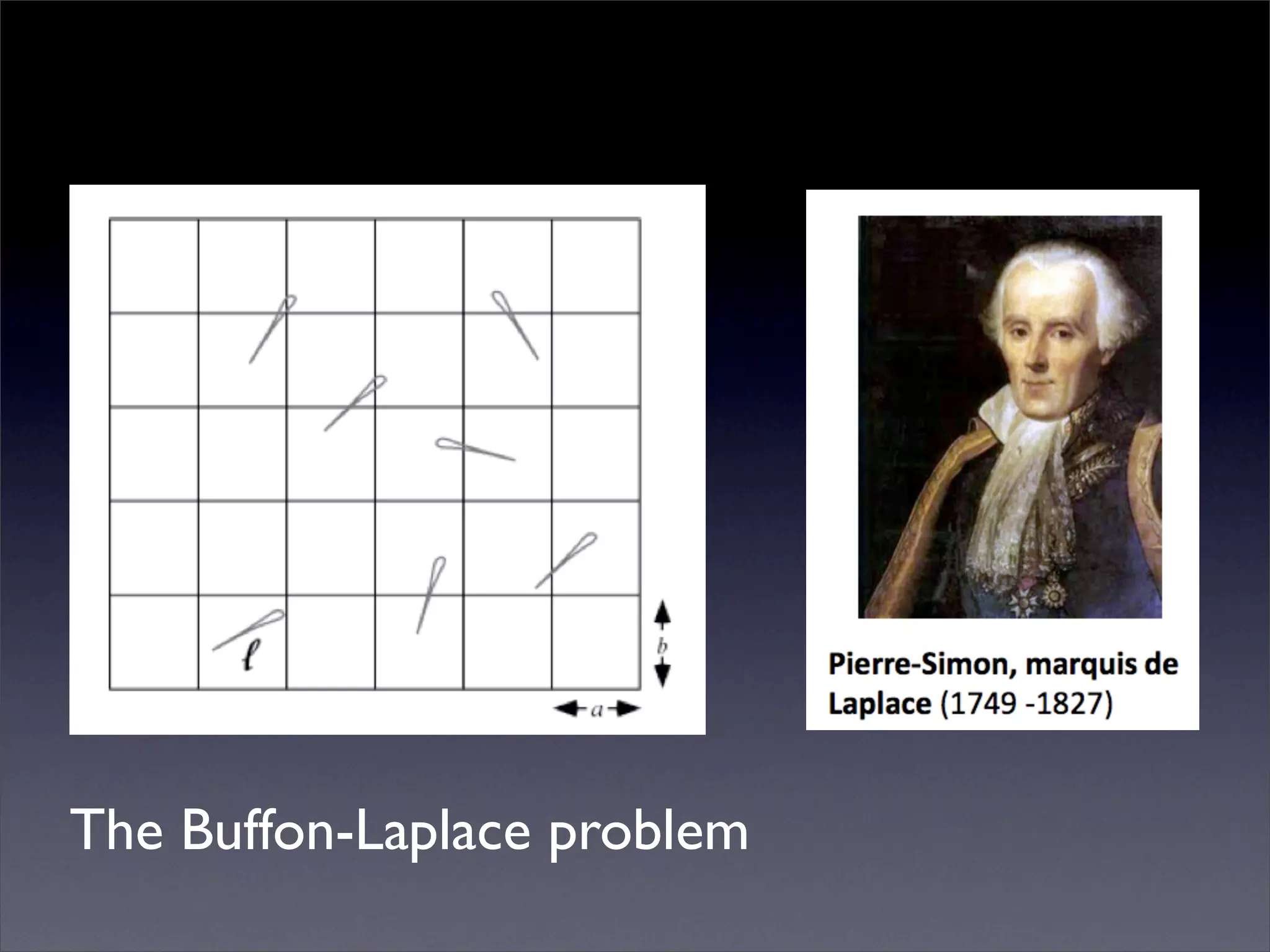
Georges-Louis Leclerc, Comte de Buffon introduced three classical probability problems including the Buffon's needle problem where the probability of a needle crossing a line on a checkerboard can be used to estimate pi. In 1901, Mario Lazzarini performed an experiment dropping a needle 3408 times and observed 1808 hits, allowing him to accurately estimate pi. The Buffon noodle problem extended this to estimate the expected number of line crossings for non-straight objects.

1. Buffon’s needle:
fun and fundamentals
Yanwei Wang

2. Georges-Louis Leclerc, Comte de Buffon
(7 September 1707 – 16 April 1788)

3. Histoire Naturelle, Générale et Particulière
(1749-88, 36 volumes)

4. Essai d’arithmétique morale
(or “Essay of moral arithmetic”)

5. The game of franc-carreau
(The clean tile problem)

6. The game of franc-carreau
(The clean tile problem)

7. The game of franc-carreau
(The clean tile problem)

8. The clean tile problem represents the first
attempt towards computing probabilities
by using geometry instead of analysis.
A.M. Mathai : An Introduction to Geometrical Probability: Distributional
Aspects with Applications, Gordon and Breach, Newark, (1999).

9. The needle problem

10. • Ever helpful, Buffon points out that "On peut
jouer ce jeu sur un damier avec une aiguille
à coudre ou une épingle sans tête."
(You can play this game on a checkerboard
with a sewing-needle or a pin without a
head.)

12. The probability that a needle (L<D) cut a line is
2L
P =
πD
The solution required a geometrical (rather than combinatorial)
approach and was obtained by using integral calculus, for the
first time in the development of probability.
A.M. Mathai : An Introduction to Geometrical Probability: Distributional
Aspects with Applications, Gordon and Breach, Newark, (1999).

13. The probability that a needle (L<D) cut a line is
2L
P =
πD
Buffon's needle problem established the theoretical
basis for design-based methods to estimate the
total length and total surface area of non-classically
shaped objects.
The field is known as Stereology.

14. Proc Biol Sci. 2000 April 22; 267(1445): 765–770.

15. The probability that a needle (L<D) cut a line is
2L
P =
πD
In 1812, Laplace suggested using Buffon’s needle
experiments to estimate π

16. The Monte Carlo Casino
Von Neumann chose the name "Monte Carlo".

17. The probability that a needle (L<D) cut a line is
2L
P =
πD
In 1812, Laplace suggested using Buffon’s needle
experiments to estimate π
wrong!

18. An italian mathematician, Mario Lazzarini performed the
Buffon’s needle experiment in 1901. His needle was 2.5
cm long, and his parallel lines were separated by 3.0 cm
apart. He dropped the needle 3408 times and observed
1808 hits.
1808 2 2.5
=
3408 π 3.0
ˆ
355
π=
ˆ = 3.1415929...
113

19. An italian mathematician, Mario Lazzarini performed the
Buffon’s needle experiment in 1901. His needle was 2.5
cm long, and his parallel lines were separated by 3.0 cm
apart. He dropped the needle 3408 times and observed
1808 hits.
1808 2 2.5
=
3408 π 3.0
ˆ
355
π=
ˆ = 3.1415929...
113
The Zu Chongzhi Pi rate, obtained
around 480 using Liu Hui's algorithm
applied to a 12288-gon Zu Chongzhi
(429–500)

21. What is the average number of needle-line crossings?
This version was introduced by Émile Barbier (1839-1889) in 1870.

22. If L<D, the number of crossing in one throw can
either be 1 or 0 with probabilities P and 1-P.
The throws are Bernoulli trials.
2L
P =
πD
When a needle is dropped at random T times, the
expected number of cuts is PT.

23. The Buffon Noodle Problem

24. Suppose the noodle is piecewise linear, i.e. consists
of N straight pieces. Let Xi be the number of times
the i-th piece crosses one of the parallel lines. These
random variables are not independent, but the
expectations are still additive.
E(X1+X2+···+XN)=E(X1)+E(X2)+···+E(XN)
Ramaley, J. F. (1969). "Buffon's Noodle Problem". The American Mathematical Monthly
76 (8, October 1969): 916–918

25. When a noodle is dropped at random T times,
the expected number of cuts is PT.
2L
P =
πD
where L is the contour length of the noodle.

26. Consider a circle with diameter, D, the same as
the grid spacing. The total length of the circle
(circumference) is π D. The expected number
of cuts per throw is then
2 πD
=2
π D

28. The Buffon-Laplace problem

30. Summary
• Mr. Buffon and his three classical problems
• Mr. Lazzarini’s lucky estimate of π
• The Buffon noodle problem
• Inspirations to our research