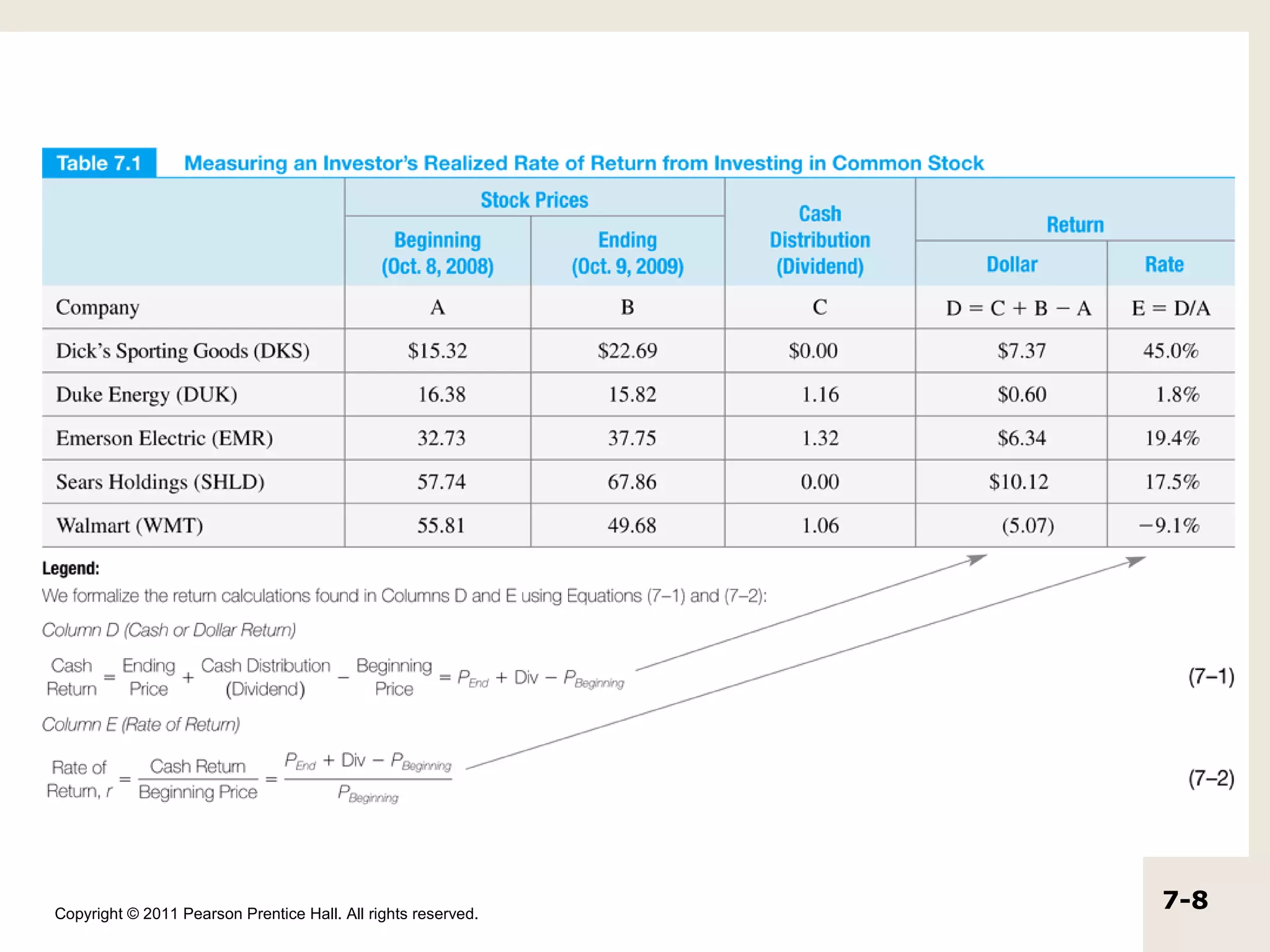
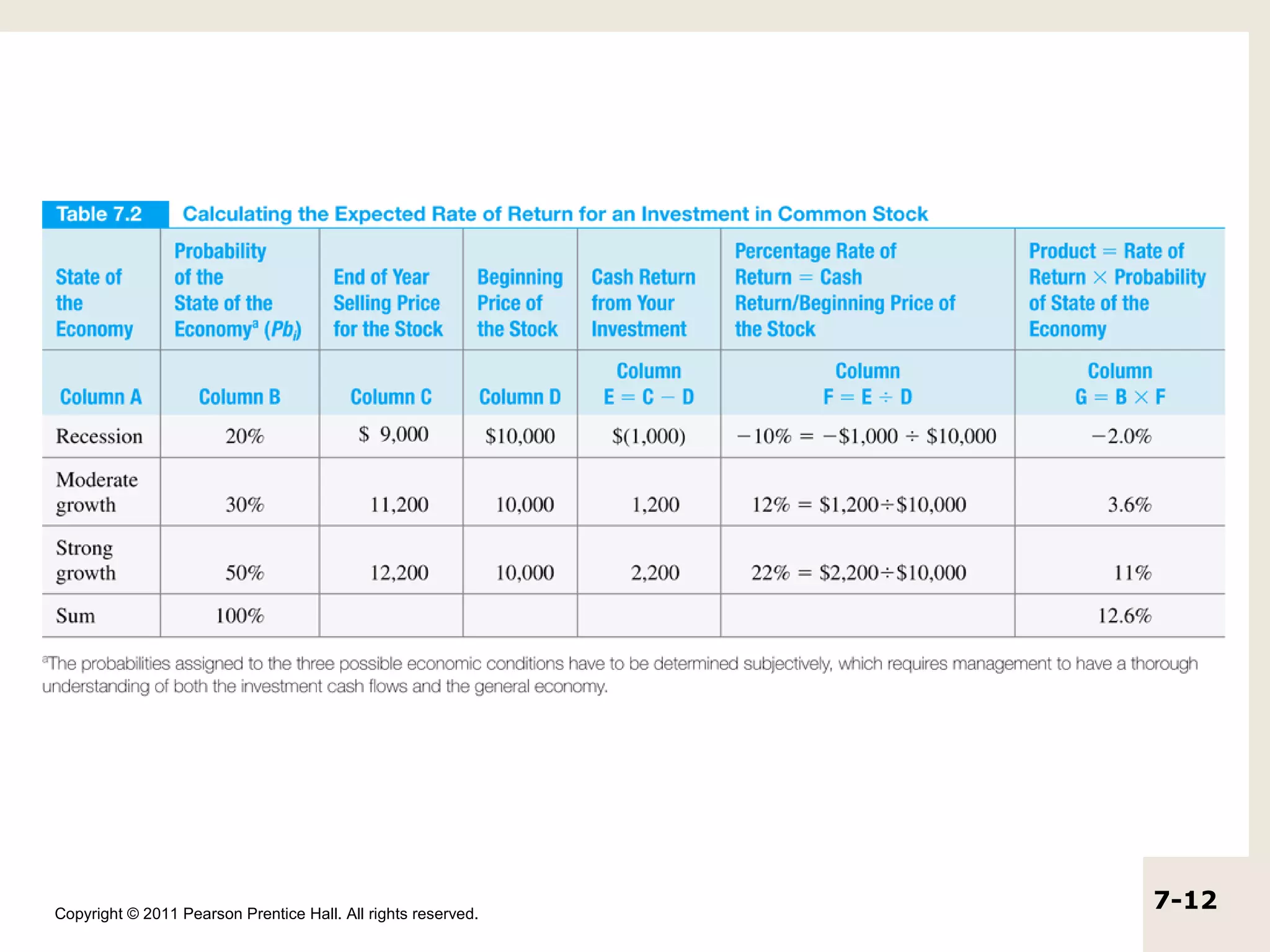
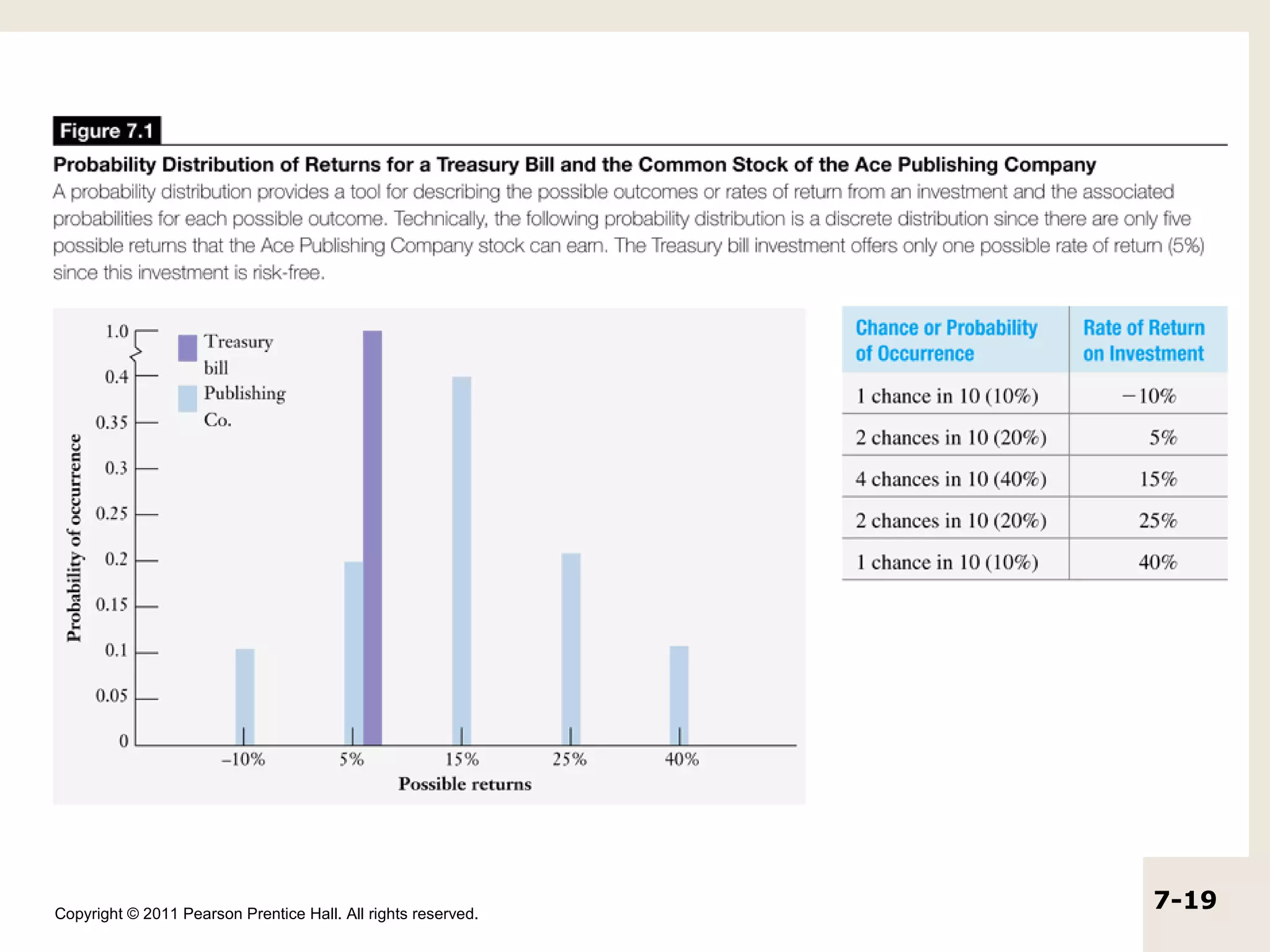
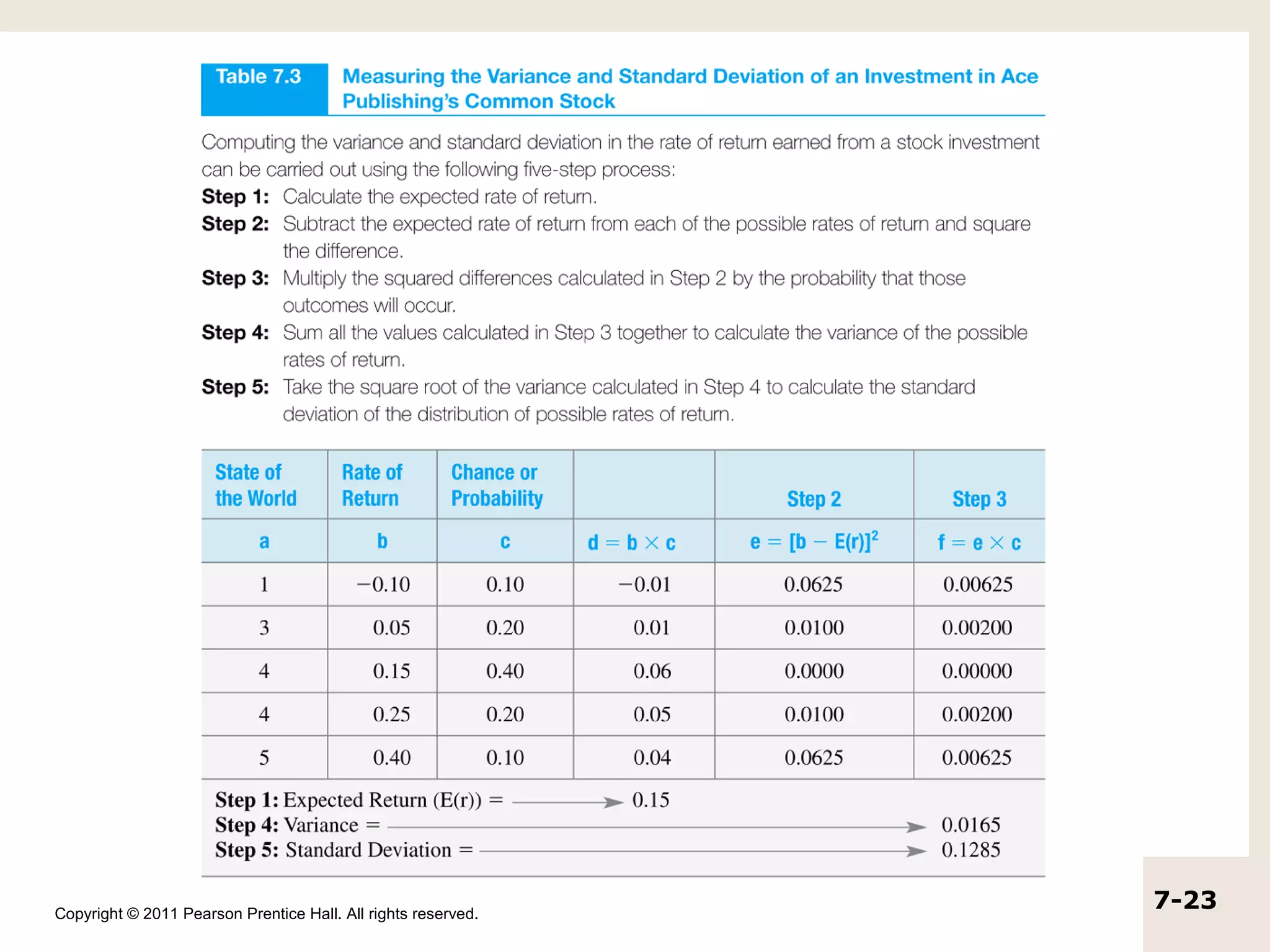
The document discusses the concepts of realized return, expected return, risk, and the efficient market hypothesis. It provides examples of calculating realized returns from investments in stocks and defines expected return as the average of possible future returns weighted by their probabilities. Risk is measured using variance and standard deviation, with higher values indicating greater risk. The efficient market hypothesis suggests that market prices reflect all available information.




























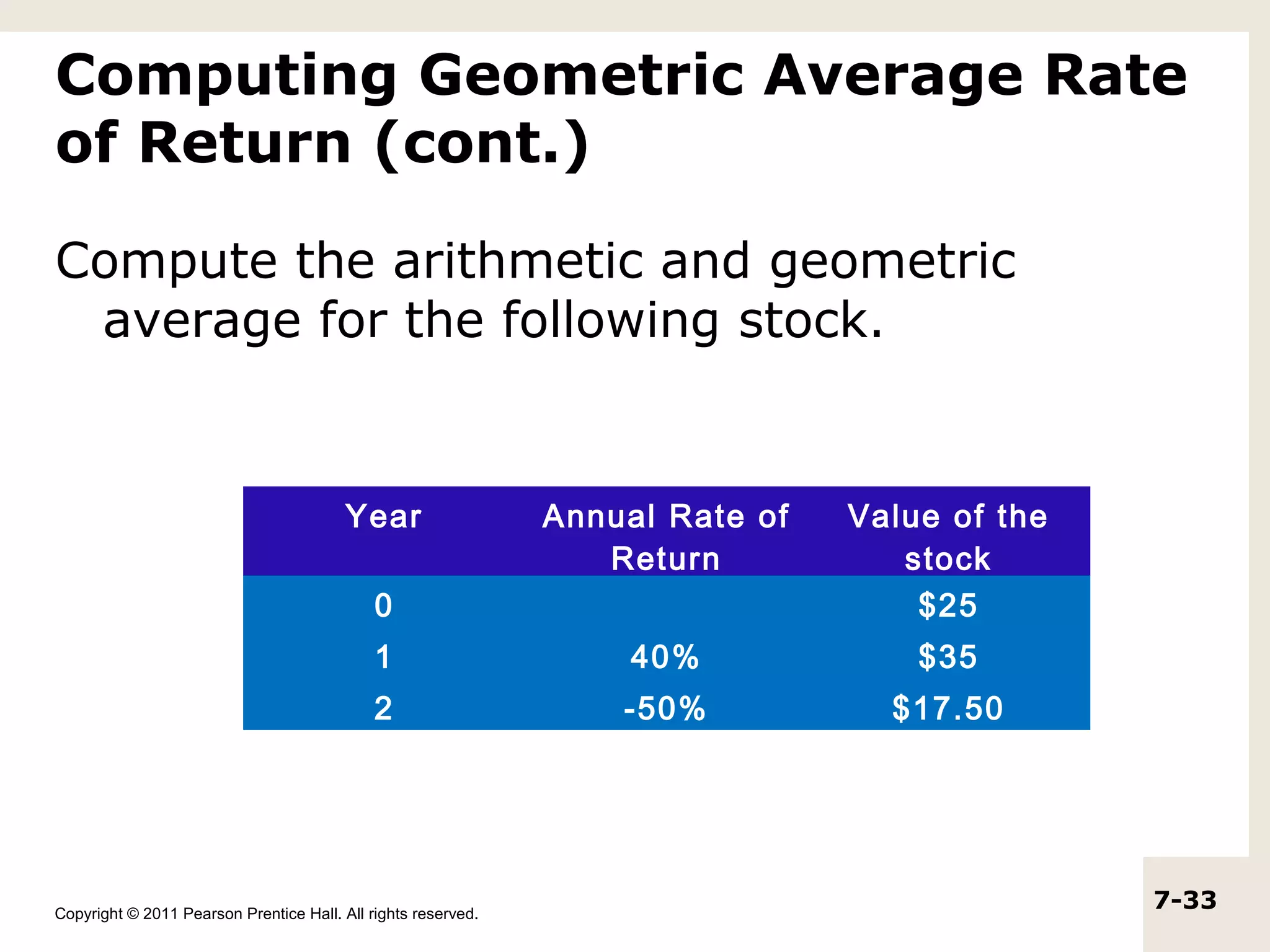
![Computing Geometric Average Rate
of Return (cont.)
• Arithmetic Average = (40-50) ÷ 2 = -5%
• Geometric Average
= [(1+Ryear1) × (1+Ryear 2)]1/2 - 1
= [(1.4) × (.5)] 1/2 - 1
= -16.33%
Copyright © 2011 Pearson Prentice Hall. All rights reserved.
7-34](https://image.slidesharecdn.com/chapter7anintroductiontoriskandreturn-130320131500-phpapp02/75/Chapter-7-an-introduction-to-risk-and-return-34-2048.jpg)






